关于开放式基金风险分析与评价的模型构建

周 林

(连云港开放大学，江苏 连云港 222006)

关于开放式基金风险分析与评价的模型构建

周 林

(连云港开放大学，江苏 连云港 222006)

以开方式基金投资8个不同项目为例建立数学模型，首先解决怎样投资可获得最大利润；进一步考察对投资有影响的项目，进一步解决怎样投资使利润最大而风险最小，给出了比较完整的模型。先用计算机VB语言进行编程计算出结果，然后加入投资者对风险和投资利润的偏好，建立有权重的单目标线性规划模型。

开放式基金;风险分析;风险评价

一、问题重述

某开放式基金现有总额为15亿元的资金可用于投资，目前共有8个项目可供投资者选择，每个项目可重复投资。根据专家经验，对每个项目投资总额不能太高，应有上限。这些项目所需要的投资额已知，一般情况下投资一年后各项目所得利润也可估算出来，如表1所示。

表1 项目内容列表 万元

请帮该公司解决以下问题：

(1)就表1提供的数据，应该投资哪些项目，使得第一年所得利润最高？

(2)在具体投资这些项目时，实际还会出现项目之间互相影响的情况。公司咨询有关专家后，得到以下可靠信息：同时投资项目A1，A3，它们的年利润分别是1 005万元，1 018.5万元；同时投资项目A4，A5，它们的年利润分别是1 045万元，1 276万元；同时投资项目A2，A6，A7，A8，它们的年利润分别是1 353万元，840万元，1 610万元，1 350万元。该基金应如何投资？

(3)如果考虑投资风险，则应如何投资，使收益尽可能大，而风险尽可能小。投资项目总体风险可用投资项目中最大的一个风险来衡量[1]119-120。专家预测出各项目的风险率，如表2所示。

表2 项目风险率

(4)开放式基金一般要保留适当的现金，降低客户无法兑现的风险。在这种情况下，将专家的信息都考虑进来，基金该如何决策，使得尽可能降低风险，而一年后所得利润尽可能多？

(5)这个项目投资，是必须资金全部到位才有利润，还是只要第一期资金到位启动后就可以随便投资，然后利润率按第一期利润和投资之比来计算？

二、模型假设

(1)假定在15亿元资金尽可能地用完前提下，风险最小。

(2)对相互有影响的项目投资，投资次数相同，则都按有影响投资的利润计算即可；投资次数不同，相减后，有相同投资次数部分按有影响投资的利润计算，次数多的项目多余部分按原利润计算[2]116-118。

三、问题分析

问题1：参照表1可得，对8个项目进行投资时，先对某个项目利润率较大的进行投资，而且尽可能投资多一些，其次再对利润率次大的进行投资，如此进行投资下去。

问题2：在对8个项目进行投资时，由于出现项目之间相互影响，相互影响的项目的利润发生了变化。在进行项目投资时，先要计算几个项目的平均利润率，然后再将8个项目的利润率与平均利润率相比较，投资时按利润率从大到小的顺序进行，投资时还要注意项目之间相互影响的关系[3]92-97。题目中所讲的“同时”具有双重意思：

第一，有相互影响的项目投资时，若投资的次数相同，投资利润就都按变化后的利润计算；若投资次数不同时，就将投资次数相同按变化后的利润计算，剩余的次数按变化前的利润计算。

第二，有相互影响的项目投资时，只要它们一起投资，不管投资的次数是否相等，都按变化后的利润计算。

本论文着重讨论第一种情况，对于第二种情况将在模型的讨论与评价中分析。

问题3：根据题目中的要求使收益尽可能大，且风险尽可能的小，这就要求建立一个双目标规划函数：即一个是用来衡量利润最大的一个方程；另一个是用来衡量风险最小的一个方程。根据投资者对风险和投资利润的偏好，引入偏好系数μ，建立有权重的单目标线性规划模型。

问题4：由于开放式基金一般要保留适量的现金，降低客户无法兑付现金的风险。经过查阅有关资料，假定适量的现金就是投资该项目资金的10%。

四、模型建立[4]79-83

(一)符号的说明

Ai：投资第i项目的编号；

ni：投资第i项目的次数；

Qi：投资第i项目风险损失率；

Bi：一次投资第i项目所需的资金；

Hi：第i项目投资额的上限；

Ki：投资第i项目的预计利润；

Xi：投资第i项目的次数；

Xij：同时投资第i,j项目的次数；

Xi′：除去Xij投资第i项目的次数；

S：总利润；C：总风险；μ：偏好系数。

(二)求出Ai最多所投资ni

(1)

由公式(1)可求出各投资项目的有关数据。见表3。

表3 各投资项目的有关数据

问题1：要使第一年所得利润最大

我们可以得出

(2)

将目标函数进一步化解：

S=Max(1139X1+1056X2+727.5X3+1265X4+1160X5+714X6+1840X7+1575X8)限制条件如下所示：

X1，X5，X6，X7，X8∈[0,5];X2，X4∈[0，4];X3∈[0,6]

6700X1+6600X2+4850X3+5500X4+5800X5+4200X6+4600X7+4500X8≤150000

(3)

由假设(1)可以得出：

143300<6700X1+6600X2+4850X3+5500X4+5800X5+4200X6+4600X7+4500X8≤150000

(4)

这样将不等式(4)来代替不等式(3)，在计算上比较方便些，进一步减少计算的时间。

问题2：其目标函数与问题一相同，即：

将目标函数进一步化解：

其限制条件为：

问题3：使收益尽可能大，且风险尽可能的小：

双目标函数：

C=Min(Max(QiXiBi))

将目标函数进一步化解：

其限制条件为：

问题4：保留适量的现金为投资该项目资金的10%，使收益尽可能大，且风险尽可能的小：

双目标函数：

C=Min(Max(QiXiBi))

将目标函数进一步化解：

化简为单目标函数：mina=μ(-S)+(1-μ)C

其限制条件为：

∈(143300,150000]

五、模型求解

用Visual Basic对模型一进行编程，求解的结果如下表所示：

表4 问题1解释

表5 问题2解释

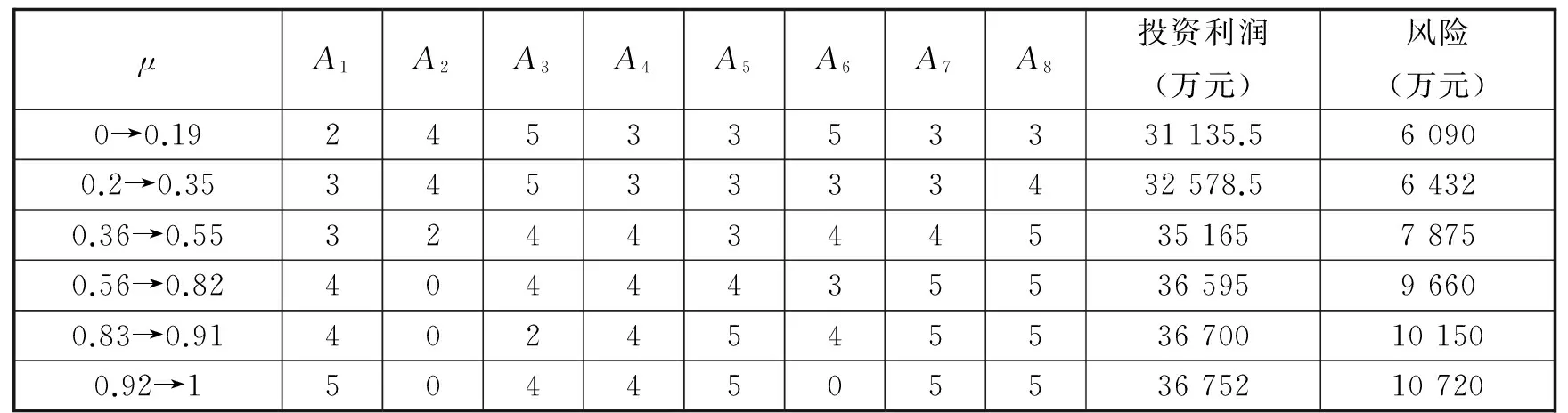
表6 问题3解释

六、模型验证

对计算机所运行的结果进行检验，检验的方法用“问题分析”中所提到的方法进行检验。即刚开始先投资利润最大的项目，然后再投资利润较大的项目，最后再投资利润小的项目。检验结果均符合要求。

七、模型讨论与评价

现在对问题2中的第2种情况进行求解，只需将目标函数中的利润S稍做改动，得出结果如下：

表8 问题2第二种情况

表9 问题3第二种情况

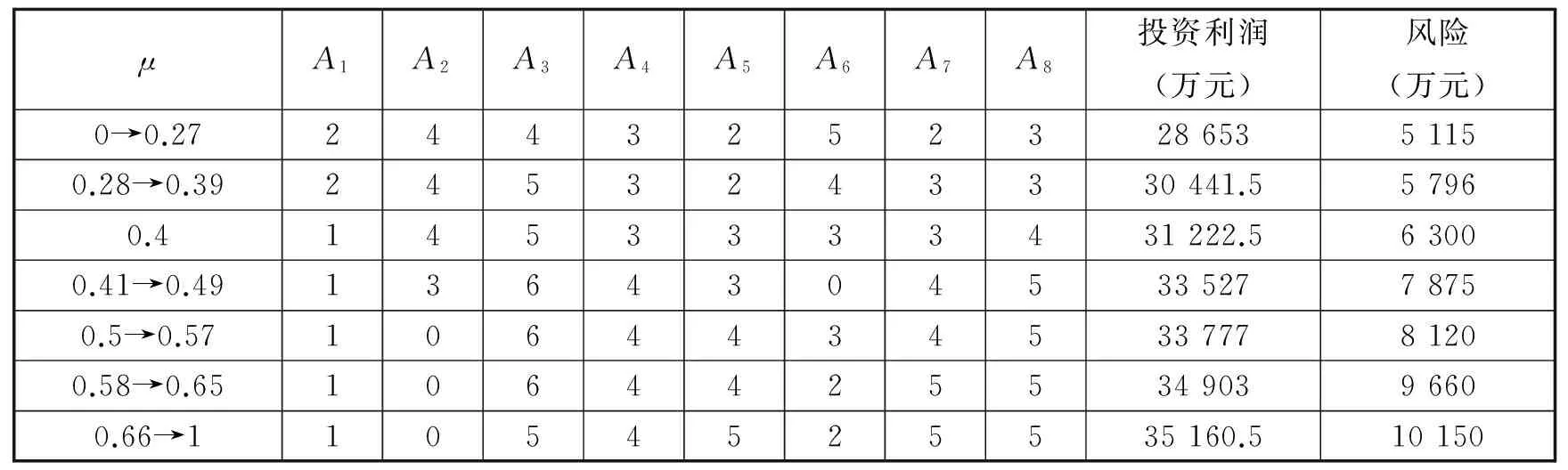
表10 问题4第二种情况

本模型根据投资者对风险和投资利润的偏好程度，引入偏好系数μ，将双目标化简为单目标，建立了有权重的单目标线性规划模型，又采用VB语言编程较完善地求得了模型的解。

[1] 汪守国, 赵彦普, 邹辉霞. 我国开放式基金的运作探讨[J]. 科技进步与对策, 2002(06).

[2] 戴振强, 曹家和. 开放式基金选股策略的实证研究[J]. 经济论坛, 2007(09).

[3] 张宗益， 谭 朋. 我国开放式基金股票配置策略与基金业绩间关系的实证研究[J]. 技术经济, 2013(07).

[4] 郑秀田. 开放式基金流动性管理的数理模型研究[J]. 杭州师范大学学报(自然科学版), 2012(05).

ModelConstructiononRiskAnalysisandAssessmentofOpen-endFunds

ZHOU Lin

(LianyungangOpenUniversity,Lianyungang222006,China)

The paper takes eight different projects of open-end funds for example, trying to set up mathematical models. First, it manages to get the most profit through the investment. Second, it tries to get the most profit with the least risk by further investigating the projects which have influence on the investment. In terms of the above two aspects, the paper gives comparatively integrate models: after using Visual Basic to programme and calculate the result, adding to appetite for the investment risk and investment profit to build weighting single-objective linear programming models.

open-end funds; risk analysis; risk assessment

F713.54

A

1671-8127(2017)05-0056-04

2017-03-29

周 林(1982- )，女,江苏连云港人，连云港开放大学讲师，主要从事应用数学研究。

[责任编辑乐知]