Cox模型变量选择的R软件实现

韦新星 赵丽棉

【摘要】本文基于R软件，对Cox模型的变量选择进行案例分析。结果表明，R软件不仅能很好地对Cox模型进行变量选择，操作简便，准确度高，而且还能绘制特定变量的生存函数图，供进一步对比分析使用。

【关键词】R Cox模型 变量选择 生存函数图

【中图分类号】G642.1 【文献标识码】A 【文章编号】2095-3089（2017）39-0217-02

一、引言

Cox模型是英国统计学家Cox于1972年提出的[1]。Cox模型一经提出，便被广泛应用于生存数据的处理和分析中。运用Cox模型进行变量选择，人们不仅可以处理内含删失数据的生存数据，而且还可以处理不服从正态分布的生存数据，这为生存数据的处理和分析提供了有效的途径。

然而，在建立Cox模型进行变量选择的过程中，由于Cox模型隶属半参数模型，模型表达式较为复杂，若按照公式进行处理，则不仅计算量大，而且还容易出错。为此，本文在前人研究的基础上，基于R软件，对Cox模型的变量选择进行R软件的实现研究，以解决上述问题带来的影响。

二、Cox模型概述

Cox模型，又称Cox比例风险模型，是一种处理多因素生存数据的有效方法。其一般形式为：

其中，为协变量，为回归系数，为与无关的基本风险函数。之所以又将Cox模型称为Cox比例风险模型，是因为对于不同的协变量和，该模型都能满足一个特点，即风险函数之比与无关，类似于没有的情况[2]。于是通常用风险函数来描述被观测对象在某一时间点存活的条件下，在未来时间里死亡的概率。另一方面，個体生存时间大于时间的概率被命名为生存函数。

Cox模型中的回归系数通常用偏似然函数来估计[4]。而生存分析中的很多检验也都是基于似然函数或偏似然函数的渐进性质实现的，如似然比检验、Wald检验和得分检验等，若这些检验的统计量值大于临界值，或检验统计量的P值小于检验水平，则拒绝原假设，认为回归系数有显著影响。

三、R软件实现

本节从典型的生存案例出发，基于R软件，实现Cox模型变量选择的过程。

案例采用72个乳腺癌病人的数据，数据来源于文献[3]，共包含4个变量：time，index，age和group，分别表示生存时间、删失情况（1表示死亡，0表示删失）、年龄和是否用药（2表示用了抗癌药，1表示没用抗癌药）。其中，年龄为定量数据，是否用药为定性数据。现要探究患者手术时的年龄与是否用药对乳腺癌患者术后生存状况的影响。

经分析，这是一个典型的生存分析问题，宜采用Cox模型来研究age和group这2个协变量对生存时间time的影响。具体操作如下：

1.数据处理

由于文献[3]的数据为sav格式，故需将其另存为逗号分隔符文件（csv格式）或文本文件（txt格式），然后再用read.csv（）或read.table（）方法进行读取。在此，我们以另存为到桌面的csv格式为例。步骤：在SPSS的数据视图中，通过选择“文件”→“另存为”，然后在“保存类型”下拉列中选择csv，以文件名“案例一”另存为到桌面即可。

2. R代码编写

接下来，运用R软件进行Cox模型变量选择。

（1）先在R中安装survival包。可通过点击“Packages”→“Load package”，然后在弹出的select one选择框中选择survival，然后点击“OK”。此时R中会出现以下语句：

> local（{pkg <- select.list（sort（.packages（all.available = TRUE）），graphics=TRUE）

+ if（nchar（pkg）） library（pkg， character.only=TRUE）}）

Loading required package： splines

接着，用R代码library（survival）进行加载即可。

（2）然后在R中输入R代码。需要指出的是，R中的所有代码都区分大小写，而且其标点符号都需要用半角格式书写。Cox模型变量选择的R代码为：

u=read.csv（"C：/Users/Administrator/Desktop/案例一.csv"，sep="，"）

library（survival）

a=coxph（Surv（time，index）～age+group，data=u）

sa=step（a）

summary（sa）

回车后即可看到Cox模型变量选择的输出结果。

此外，运用R软件还可以进行生存函数图的绘制。在R中输入以下R代码：

a0=survfit（Surv（time，index）～group，data=u，type="kaplan-meier"）

plot（a0，lty=1：2，xlab="time"，ylab="survival fuction"）

title（"comparison"）

legend（"topright"，c（"group=1"，"group=2"），lty=1：2）

回车后即可看到生存函数的对比图。

3.结果输出及分析

（1）Cox模型变量选择的部分输出结果如下：

Call：

coxph（formula = Surv（time， index） ～ age + group， data = u）

n= 72， number of events= 36

coef exp（coef） se（coef） z Pr（>|z|）

age 0.2076 1.2307 0.0323 6.423 1.34e-10 ***

group -1.5269 0.2172 0.4086 -3.737 0.000186 ***

---

Signif. codes： 0 ‘*** 0.001 ‘** 0.01 ‘* 0.05 ‘. 0.1 ‘ 1

Concordance= 0.883 （se = 0.055 ）

Rsquare= 0.6 （max possible= 0.978 ）

Likelihood ratio test= 65.91 on 2 df， p=4.885e-15

Wald test= 47.6 on 2 df， p=4.608e-11

Score （logrank） test = 60.62 on 2 df， p=6.872e-14

可以看到，age和group這2个协变量的系数分别为0.2076和-1.5269，其中age的系数为正，表明高龄乳腺癌患者的死亡率高于低龄的，而group的系数为负，表明用了抗癌药的乳腺癌患者的死亡率低于没用药的。Cox模型表达式为：

另一方面，为0.6，表明模型的拟合效果较好。而似然比检验、Wald检验和得分检验的P值均小于0.001，可认为回归系数有显著影响。

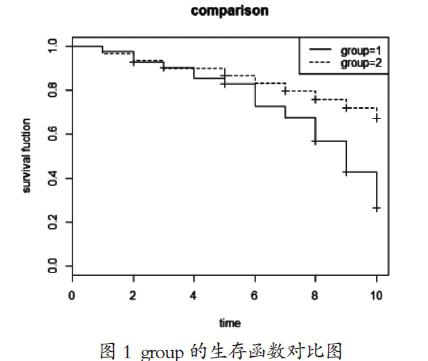
（2）绘制的生存函数对比图为：

图1 group的生存函数对比图

由图1，我们可以比较用了抗癌药的乳腺癌患者（group=2）和没用抗癌药的乳腺癌患者（group=1）的生存函数的区别。可以看到，用了抗癌药的乳腺癌患者的生存状况明显高于没用药的，这再次表明用药对抗癌有明显疗效。

四、结论

本文基于R软件，对Cox模型的变量选择进行研究分析。从案例的编程及处理上看，尽管数据结构不尽相同，但在对Cox模型进行变量选择时，R软件操作简便，实用性强，准确度高，能很好地对Cox模型进行变量选择。此外，R软件还可生成特定变量的生存函数图，不仅直观形象，还可供进一步对比分析使用。

参考文献：

[1] COX D R. Regression Models and Life Tables[J]. Journal of Royal Statistical Society， 1972， 34： 187-220.

[2] 吴喜之. 统计学：从数据到结论[M]. 北京： 中国统计出版社， 2013： 200-207.

[3] 李静萍， 谢邦昌. 多元统计分析方法与应用[M]. 中国人民大学出版社， 2008： 209-217.

[4] 田俊. Cox回归模型及其参数估计[J]. 福建医学院学报. 1987， 21（2）： 115-117.

基金项目：河池学院硕士专业学位建设基金课题（2016YT004）；广西大学生创新创业训练计划项目（201610605054）。

作者简介：韦新星（1990-），女，广西柳州人，河池学院数学与统计学院助教，硕士，研究方向：应用统计。