三电平逆变器电流谐波最小PWM方法
徐 渊,宋文祥,冯九一,杨 影
三电平逆变器电流谐波最小PWM方法
徐 渊,宋文祥,冯九一,杨 影
(上海大学机电工程与自动化学院,上海200444)
三电平逆变器在中高压大功率交流系统中的应用越来越广泛,但随着工作电压等级提高,开关损耗也随之增大.降低功率器件的开关频率可减少大容量逆变器的工作损耗,同时也会带来电流谐波畸变较大的问题,因此需要采用特殊的优化脉冲调制策略.研究了一种二极管箝位三电平逆变器(three-level neutral point clamped,3L-NPC)在低开关频率运行下的电流谐波最小脉宽调制(current harmonic minimum pulse width modulation,CHMPWM)分段同步调制方法.通过理论计算得到分段同步调制方案,采用遗传算法(genetic algorithm,GA)和序列二次规划(series quadratic programming,SQP)算法求取开关角,最后通过仿真和实验验证了理论分析的正确性及CHMPWM性能的优越性.
三电平逆变器;低开关频率;电流谐波最小
三电平逆变器在高压大功率牵引传动场合有着广泛的应用.但是,随着工作电压等级的提高,逆变器输出功率增大,开关损耗也会相应增大,这对器件散热以及寿命都带来严峻考验,其解决方法就是降低开关器件的开关频率以增大逆变器的输出功率[1].Holtz等[2]给出了在3.6 kV直流电压、80°C器件结温的情况下Eupec公司6.5 kV,600 A的绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)最大输出负载电流的有效值(Irmsmax)与开关频率(fsw)的关系曲线.当开关频率从800 Hz减小到200 Hz时,IGBT的最大输出电流可增大1倍,因此降低开关器件的开关频率可以有效增大逆变器的最大输出功率.但是传统的脉宽调制(pulse width modulation,PWM)方法,如空间矢量脉宽调制(space vector PWM,SVPWM)方法在低开关频率运行时会使输出电压和电流中谐波的含量增大[3],导致电机损耗增大,发热严重,故不适合应用在低开关频率下.因此,低开关频率下的PWM调制策略作为高压大功率牵引传动系统的核心技术,得到了越来越多的关注[4].
目前,针对低开关频率下的PWM调制方式,国内外学者已经进行了大量的研究,提出了多种优化方法,主要有转矩脉动最小PWM[5]、特定谐波消除PWM(selected harmonic elimination PWM,SHEPWM)[6]、电流谐波最小PWM(current harmonic minimum PWM,CHMPWM)[7]等.由于转矩脉动最小PWM优化方程的建立含有特定的电机参数及瞬时转速等信息,为了满足在特定工况下的优化目标,需要对优化方程实现在线实时求解;同时电机参数等变量随着电机运行情况实时发生变化,难以保证开关角求解的准确性.SHEPWM开关角的求解不需要电机参数,因此具有较好的通用性,但由于SHEPWM消除的低次谐波的能量转移到高次谐波,使得临近的高次谐波幅值明显增大,导致其对应的电流谐波幅值较高,引起转矩脉动的增大.
CHMPWM是直接以电流谐波总畸变率作为开关角计算的性能指标,能在保证逆变器输出基波电流为期望值的前提下尽可能减小谐波电流的有效值,使得输出电流具有最佳谐波特性[6].CHMPWM的目的是使输出电流具有最小的谐波畸变率,并不会出现SHEPWM中未消除的高次谐波被明显放大的现象,并且求解出的开关角同样具有较好的通用性.不过,由于CHMPWM求解更加复杂,实际应用也不如SHEPWM广泛.
本工作首先对CHMPWM的基本原理给出分析,通过计算得到了分段同步调制策略.基于遗传算法(genetic algorithm,GA)求取开关角初值,并将初值代入电流谐波总畸变率表达式中,采用序列二次规划(series quadratic programming,SQP)算法得到期望的开关角.最后通过仿真和实验进行了验证.
1CHMPWM原理
1.1 优化PWM波形描述与分析
CHMPWM是基于开关角直接计算的调制方法.通过对逆变器输出波形进行傅里叶分析,可以得到电压基波幅值及各次谐波幅值关于开关角的精确数学关系,由此便可根据期望的优化目标来定量地求解各个开关角,从而使逆变器输出电流具有最优的谐波特性.
图1和2分别为二极管箝位三电平逆变器(three-level neutral point clamped,3L-NPC)拓扑结构和单相PWM输出电压波形.为了简化非线性约束方程组的求解,通常令PWM输出波形具有1/4周期对称性.
对图2所示的电压波形进行傅里叶分解可得到

式中,a0=an=0,t为时间,

其中bn为各次谐波电压幅值,N 为1/4周期内开关角数量,αk满足0≤ α1< α2< ···<αn≤π/2.

图1 3L-NPC逆变器拓扑结构Fig.1 Topological structure of 3L-NPC inverter

图2 单相PWM输出相电压波形Fig.2 Output single-phase PWM voltage waveform
1.2 CHMPWM数学模型
CHMPWM是直接以系统电流的畸变率作为开关角度计算的性能指标.虽然这种调制方式的计算依赖于负载的性质,但对于三相交流电机负载来说,其谐波等效电路阻抗将主要由定转子漏感所决定[7].
在三电平逆变器工作时,当电路带阻感负载,且电感未饱和,电阻可忽略.又考虑到三相电路中不含3次谐波,因此各次谐波电流的幅值为

式中,L为电感值,此时系统谐波电流有效值可以表示为

定义电流总谐波畸变率(total harmonics distortion,THD)为

令式(4)为求解CHMPWM开关角的目标函数,定义调制度m为基波电压u1与六拍方波运行时基波电压u1,six-step的比值:

式中,b1为电压基波幅值,Ud为直流母线电压.
由式(1)中b1表达式和式(5)得到求解开关角的非线性约束方程为

1.3 分段同步调制方案
在恒压频比变频调速控制中,在不考虑电压补偿的情况下,有

式中,f为实际基波频率,fr为电机额定频率.
在变压变频驱动系统中,为了使逆变器输出电流谐波性能达到最优,需要采用分段同步策略,根据不同调制区间选取不同的开关角数量[8].本工作研究的是额定频率为50 Hz、逆变器最大开关频率为250 Hz时的分段同步策略:

式中,1/4基波周期内的开关角数量N为整数, fl oor(·)为对括号内的值向下取整,为最大开关频率.
由式(7),(8)可以看出,随着逆变器输出频率的降低,调制度也随之减小,开关角数量则越来越大.
随着开关角数量的增加,求解开关角的计算量和实现难度也随之增大.当逆变器输出频率降低到一定程度后,CHMPWM并不比传统的PWM方法效果更好,此时同步优化调制的优势已经丧失.通常,在m<0.3时需要考虑采用异步调制策略[9].图3和4给出了不同调制度与开关角数量及开关频率之间的关系.在这种分段同步策略下,开关角数量N由5~15变化,而逆变器开关频率保持在200~250 Hz范围内.

图3 调制度和开关角数量的关系Fig.3 Relationship between modulation index and switching angles

图4 调制度和开关频率的关系Fig.4 Relationship between modulation index and switching frequency
2 开关角优化求解
2.1 GA求解初值
CHMPWM优化开关角求解的实质是一个条件极值求解问题,且优化目标函数为非线性,故其求解过程中初值的选择十分重要,合适的初值可以大大加快求解的收敛速度,否则求解速度会很慢甚至发散.
传统的微分法求取初值是以调制度为0时的开关角为基础,通过对调制度逐步进行的微小递增,来求解全调制度的开关角初值,此方法求解精度低,收敛速度较慢,当开关角数量较大时,计算难度大幅度增大.随着计算机技术的发展,求解复杂的条件极值问题大多采用智能算法,Ozpineci等[10]给出了一种采用GA的多电平逆变器谐波优化方法.
GA直接对目标进行操作,不存在求导和函数连续性的限定;采用概率化的群体搜索策略,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定规则,具有良好的全局寻优能力.这些特性已被广泛地应用于各种优化求解的场合.图5为GA流程图.
GA的优化指标取决于适应度函数.令输出电压基波幅值与期望输出电压幅值之差为ε1,其余次电压谐波幅值为ε2,ε3,···,即

图5 GA流程Fig.5 Flow chart of GA

定义GA的适应度函数为

通常,在N一定的情况下,如果已知m=mi时对应开关角的解为αi,则令Δm为m的一个微小增量,使mi+1=mi+Δm.由于开关角轨迹是关于调制度变化的曲线,因此可以将αi作为求解m=mi+1时的初值,从而求解出整个调制度范围内的开关角.对于分段同步调制策略,只需要求出各段最小调制度时的开关角初值,就可以求出整段调制度范围内的开关角.本工作采用的GA参数设置如表1所示.表2给出了GA求解出的各段开关角初值.
2.2 开关角求解
对于有约束的非线性条件极值优化问题,广泛采用的是基于牛顿迭代法发展出来的SQP算法.SQP算法利用原来的非线性约束优化问题的有关信息构造出一个简单的近似优化问题,通过求解来给出对当前迭代点的修正,用一系列二次规划的解来逐次逼近原约束优化问题的最优解.SQP算法不仅具有全局收敛性,而且在选取合适迭代初值时能够具有超越线性收敛的速度.

表1 GA参数设置Table 1 Parameter settings of GA
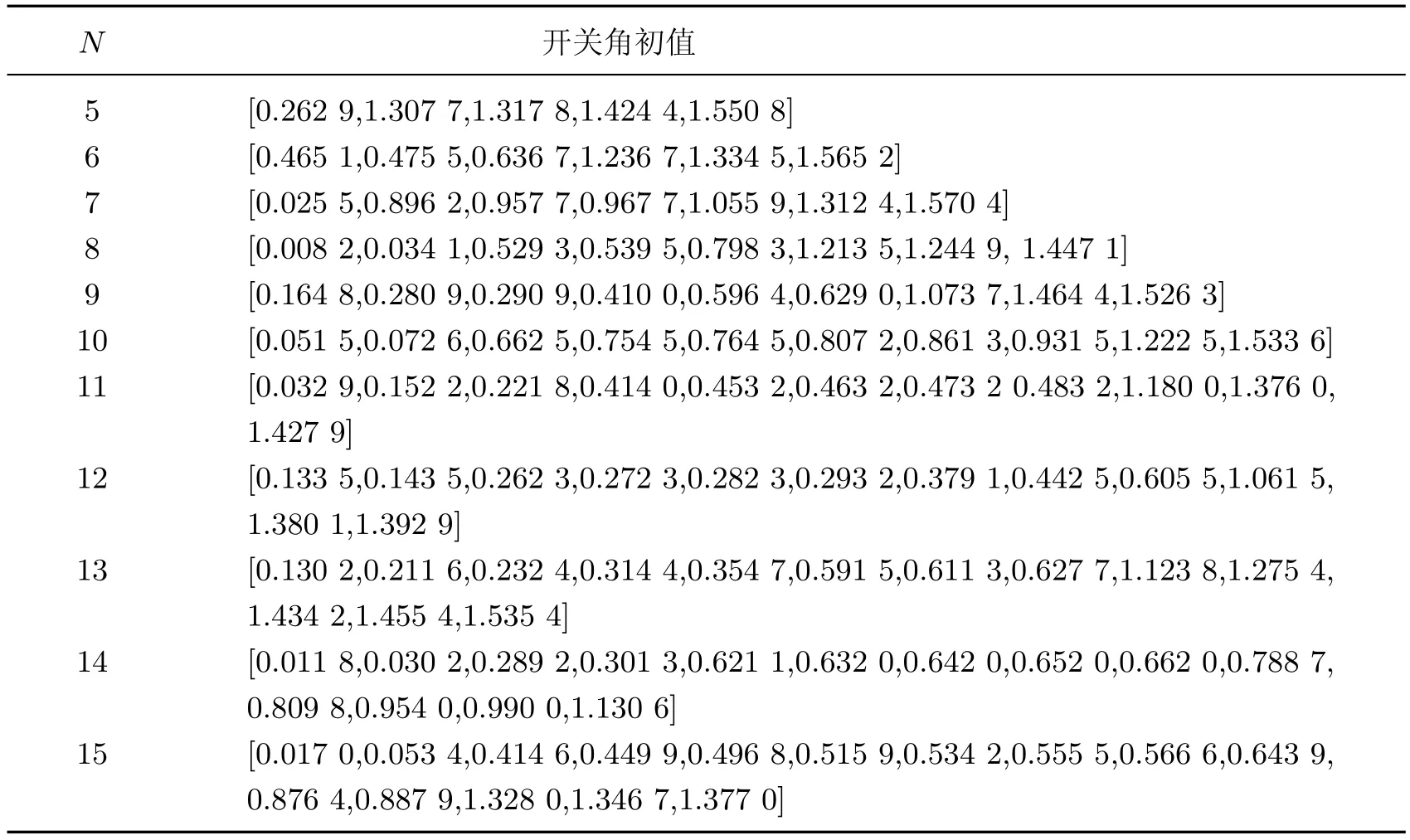
表2 开关角初值Table 2 Initial values of switching angles
Sayyah等[11]采用GA直接求解CHMPWM开关角,将电流谐波总畸变率作为适应度函数直接求解开关角.尽管GA是全局优化算法,但是由于其采用的是概率化的群体搜索策略,导致其难以保证直接求解出的CHMPWM开关角的精度,故本工作将采用GA求取的迭代开关角初值代入式(9),通过SQP算法进行优化求解,得到期望的开关角.图6和7为在相同调制策略(N=7,M=0.7)情况下采用GA直接求解开关角得到的电流频谱分析图以及采用本工作求解的开关角得到的电流频谱分析图的对比,可以看出采用本工作提出的开关角求解方法得到的电流波形具有更好的谐波特性.
3 仿真及实验验证
3.1 仿真结果
本工作利用Matlab/Simulink对上述理论分析进行了仿真建模,并通过实验进行验证.仿真中直流母线电压为540 V,负载为三相对称阻感负载,其中电阻为12.6 Ω,电感为40 mH,直流侧电容为4 700µF.根据本工作提出的分段同步调制策略以及开关角求解方案,计算得到了m∈[0.3,1.0]的开关角(见图8),得到的电流谐波总畸变率随调制度变化的曲线如图9所示.
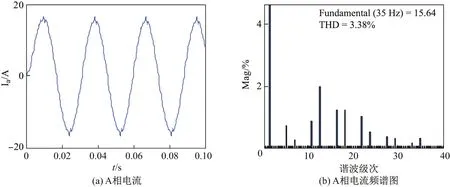
图6 GA直接求解Fig.6 Direct solution of GA
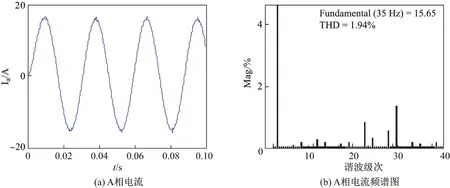
图7 GA和SQP结合求解Fig.7 Solution of GA-SQP
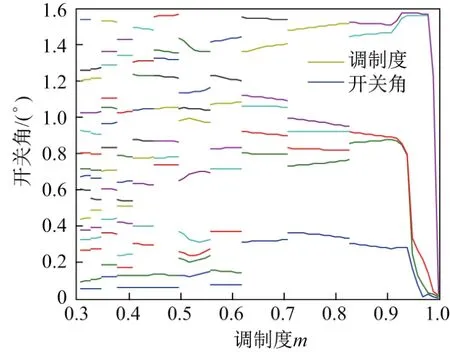
图8 调制度和开关角度曲线Fig.8 Curves of modulation index versus Switching angles
综合图8和9的结果可以看出,当开关角数量固定时,开关角和电流谐波总畸变率随着调制度的变化而平稳变化.而在开关角数量切换时,电流谐波总畸变率会发生跳变的现象,其原因是在相同开关角数量情况下求得的开关角解轨迹连续,而不同开关角数量具有不同的解轨迹,且解轨迹在开关角数量切换时不连续,因此会造成电流谐波总畸变率在开关角数量切换时产生跳变.当m大于0.95时,逆变器输出电压接近六拍方波运行时的电压,电流谐波总畸变率急剧增大.

图9 调制度-电流谐波总畸变率曲线Fig.9 Curve of modulation index versus THD
图10和11给出了调制度分别为0.4和0.8时的逆变器输出电压和电流波形,以及电流频谱图.可以看出,电流波形正弦度很高,各次谐波含量都被抑制在较低水平.
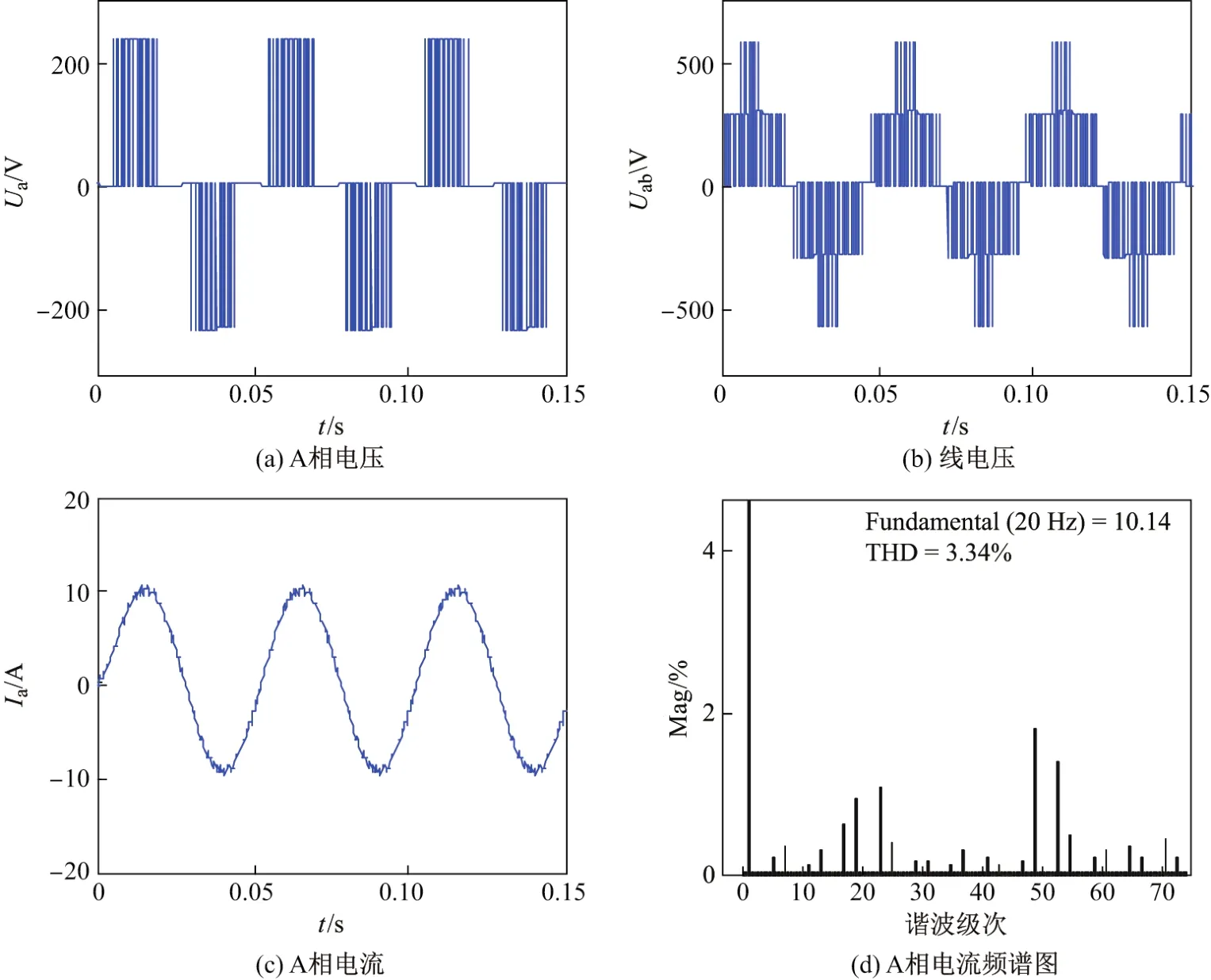
图10 m=0.4时仿真结果Fig.10 Simulation results when m=0.4

图11 m=0.8时仿真结果Fig.11 Simulation results when m=0.8
3.2 实验结果
为了进一步验证CHMPWM的可行性,需要检验计算出的开关角在实际情况中电流谐波抑制的效果,本工作基于三电平IGBT逆变器实验平台,以数字信号处理(digital signal processing,DSP)和现场可编程门阵列(f i eld-programmable gate array,FPGA)为核心控制器实现优化PWM发生器.三相对称负载电阻为1 Ω,电感为10 mH,直流侧电容为2 200µF.
图12和13是调制度m分别为0.4和0.8的电压和电流波形.从图中可以看出,实验结果与仿真结果基本一致,在每个基波中PWM脉冲数量较少,而开关频率分别为220和240 Hz的情况下,电流波形仍然保持较高的正弦度,从而也进一步证实了CHMPWM能够很好地抑制电流谐波.需要指出的是,电压波形幅值存在波动是由电容中点电压偏移所造成的.与三电平SVPWM类似,CHMPWM同样也会形成电容中性点电位的周期性变化,如何在CHMPWM中考虑实现对中性点电位波动的抑制,是一个值得进一步研究和探讨的问题.
4 结论
本工作对低开关频率运行下的NPC三电平逆变器CHMPWM方法进行详细分析,并通过系统仿真和实验验证得出如下结论.
(1)虽然CHMPWM不能像SHEPWM那样将低次谐波完全消除,但是能够将电流谐波总畸变率降到最低,从而获得更好的控制效果,有利于提高系统输出功率,降低系统损耗.

图12 m=0.4时实验结果Fig.12 Experimental results when m=0.4
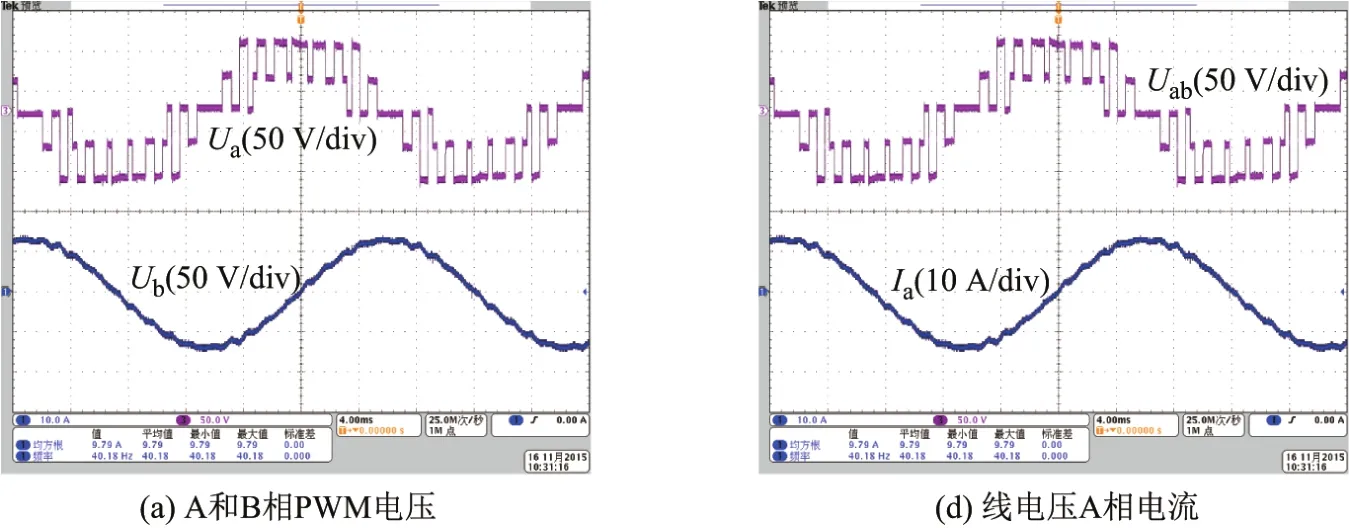
图13 m=0.8时实验结果Fig.13 Experimental results when m=0.8
(2)采用GA和SQP算法相结合的开关角求解方法,能够使得到的开关角更精确,电流波形具有更好的谐波特性.
(3)仿真和实验结果表明,在较低(250 Hz以下)的开关频率下电流谐波得到了较好的抑制,证明了所给出优化PWM方法的可行性与正确性.
[1]FRANqUELO L G,LEON J I,DOMINGUEZ E.New trends and topologies for high power industrial applications:the multilevel converters solution[C]//Proceeding of 2009 International Conference on POWERENG.2009:1-6.
[2]HOLTZ J,OIkONOMOU N.Synchronous optimal pulsewidth modulation and stator f l ux trajectory control for medium-voltage drives[J].IEEE Trans Ind Appl,2007,43(2):600-608.
[3]HOLTZ J,OIkONOMOU N.Fast dynamic control of medium voltage drives operating at very low switching frequency—an overview[J].IEEE Trans Ind Electron,2008,55(3):1005-1013.
[4]宋文祥,姜书豪,阮智勇,等.基于定子磁链轨迹跟踪的优化PWM高性能闭环控制[J].上海大学学报(自然科学版),2015,21(1):128-140.
[5]ZACH F C,MARTINEZ R,KEpLINGER S,et al.Dynamically optimal switching patterns for PWM inverter drives(for minimization of the torque and speed ripples)[J].IEEE Trans Ind Appl,1985,IA-21(4):975-986.
[6]RODRIGUEZ J R,PONTT J,HUERTA R,et al.Resonances in a high-power active-front-end rectif i er system[J].IEEE Trans Ind Electron,2005,52(2):482-488.
[7]周明磊,游小杰,王琛琛,等.电流谐波最小PWM开关角的计算及谐波特性分析[J].中国电机工程学报,2014,34(15):2362-2370.
[8]FU X,DAI P,ZHAO B J,et al.Research on subsection synchronization harmonic optimum pulsewidth modulation for inverters[C]//Proceeding of 2010 Asia Pacif i c Power and Energy Engineering Conference(APPEEC).2010:1-5.
[9]张永昌,赵争鸣.三电平变频调速系统SVPWM和SHEPWM混合调制方法的研究[J].中国电机工程学报,2007,27(16):72-77.
[10]OZpINECI B,TOLbERT L M,CHIASSON J N.Harmonic optimization of multilevel converters using genetic algorithms[J].IEEE Power Electronics Letters,2005,3(16):92-95.
[11]SAYYAH A,AFLAkI M,REZAZADE A R.Optimal PWM for minimization of total harmonic current distortion in high-power induction motors using genetic algorithms[C]//Proceeding of 2006 International Joint Conference on SICE-ICASE.2006:5494-5499.
Minimum pulse width modulation of current harmonic for three-level inverter
XU Yuan,SONG Wenxiang,FENG Jiuyi,YANG Ying
(School of Mechatronic Engineering and Automation,Shanghai University,Shanghai 200444,China)
Medium voltage transmission systems driven by a high power three-level inverter operating at low switching frequency can reduce switching losses of the power device.This paper proposes a subsection synchronous current harmonic minimum pulse width modulation(CHMPWM)approach of neutral point clamped three-level(NPC-3L)inverter in low switching frequency operation.A subsection synchronous scheme is obtained with the theoretical calculation at the allowed maximum switching frequency.Genetic algorithm(GA)is used to get high-precision initial values.The expected switching angles are achieved with as sequential quadratic programming(SQP)algorithm.Validity of the theoretical analysis and superiority of CHMPWM are verif i ed via simulation and experiments.
three-level inverter;low switching frequency;current harmonic minimum
TM 341
A
1007-2861(2017)05-0690-12
10.12066/j.issn.1007-2861.1724
2015-12-09
国家自然科学基金资助项目(51377102)
宋文祥(1973—),男,副教授,研究方向为电力电子变换和电机驱动控制.E-mail:wxsong@shu.edu.cn
本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn

