片状介质材料复介电常数优化计算及测量
周建军,张 宁, 颜锦奎
片状介质材料复介电常数优化计算及测量
周建军,张 宁, 颜锦奎
(上海大学通信与信息工程学院,上海200444)
采用终端短路同轴开口波导技术,将开口同轴波导作为传感器,测量样品加载时的复反射系数,运用优化迭代反演求得待测材料的相对介电常数.详细介绍了所采用的理论模型和测量系统,测量了一些常见介质材料的复反射系数,复反射系数参考值与理论计算值基本吻合,证明了该方法的合理性及可行性.
开口同轴波导;复反射系数;相对介电常数;优化迭代方法
迄今为止,电磁参数的计算及测量技术的研究已经历几十年[1-8].介质材料的电磁参数在现有技术下无法通过仪器直接测量得到,而是需要通过测量与电磁参数有关的参量,例如反射系数、谐振频率和驻波比等,然后根据相应参量和复电磁参数之间的数学关系进行反演计算,从而得到待测介质的复电磁参数.最传统的方法是传输/反射法,即通过矢量网络分析仪和波导探头测量加载在同轴波导末端介质的S参数,利用S参数与复电磁参数的关系进行反演推算.在此基础上,研究人员从不同角度对这项技术进行改进完善,提出了矢量分析和标量分析提取参数等技术.由于该技术设备比较简单,测量易操作,不破坏被测样品,因此应用广泛,比较适合在体测量.
本工作运用开口同轴探头技术,将片状待测介质材料作为开口同轴法兰的负载,在待测材料终端接金属短路板.理论上采用准静态模型进行谱域建模,相较于其他研究者提出的全波模型,在满足一定精确度的前提条件下降低了分析计算难度并简化了反演推导过程,加快了计算速度并降低了对计算机性能的要求.通过推导得出准静态模式下的反射系数Γc,在实验中利用矢量网络分析仪测量待测介质的反射系数Γm.将介质的相对复介电常数作为变量,建立Γc和Γm的误差函数,利用优化迭代算法,找到合适的相对复介电常数,使误差函数取最小值,将此相对复介电常数作为待测介质相对介电常数的近似值.在优化迭代时利用误差函数平方收敛,加快了计算收敛速度,简化了变量处理过程.通过对样品进行测量,将优化算法所得结果与样品测量所得的相对介电常数作比较,结果表现一致,从而在实验上证明了本方法的可行性.
1 终端短路加载片状介质同轴开口波导反射系数公式
在进行谱域建模时,需要考虑两种模型结构,分别为全波模型[9]和准静态模型[10].全波模型是按照电磁场理论严格求解得到的理论模型,在分析计算时需要考虑同轴探头内传播的所有高次模,计算过于复杂,计算难度偏大;相较于全波模型,准静态模型则忽略了同轴探头终端口附近的高次模,虽然会造成一定的误差,但是通过对误差因素进行分析和对比,该模型结果在可以接受的范围.
图1为终端短路同轴开口波导探头测量片状介质材料时的测量结构横切示意图,其中TEM代表横向电磁场(transverse electric and magnetic).同轴探头内导体外半径和外导体内半径分别为a和b,待测介质材料厚度为d.同轴探头内为空气,待测介质材料的相对介电常数和相对磁导率分别为εr和µr.本工作采用准静态模型建模分析,即在不考虑高次模影响的条件下,略去时谐因子ejωt的影响,对同轴探头内(区域1)和待测介质内(区域2)的电磁场分布进行理论推导分析,区域1中的横电磁场可以表示为[9-10]

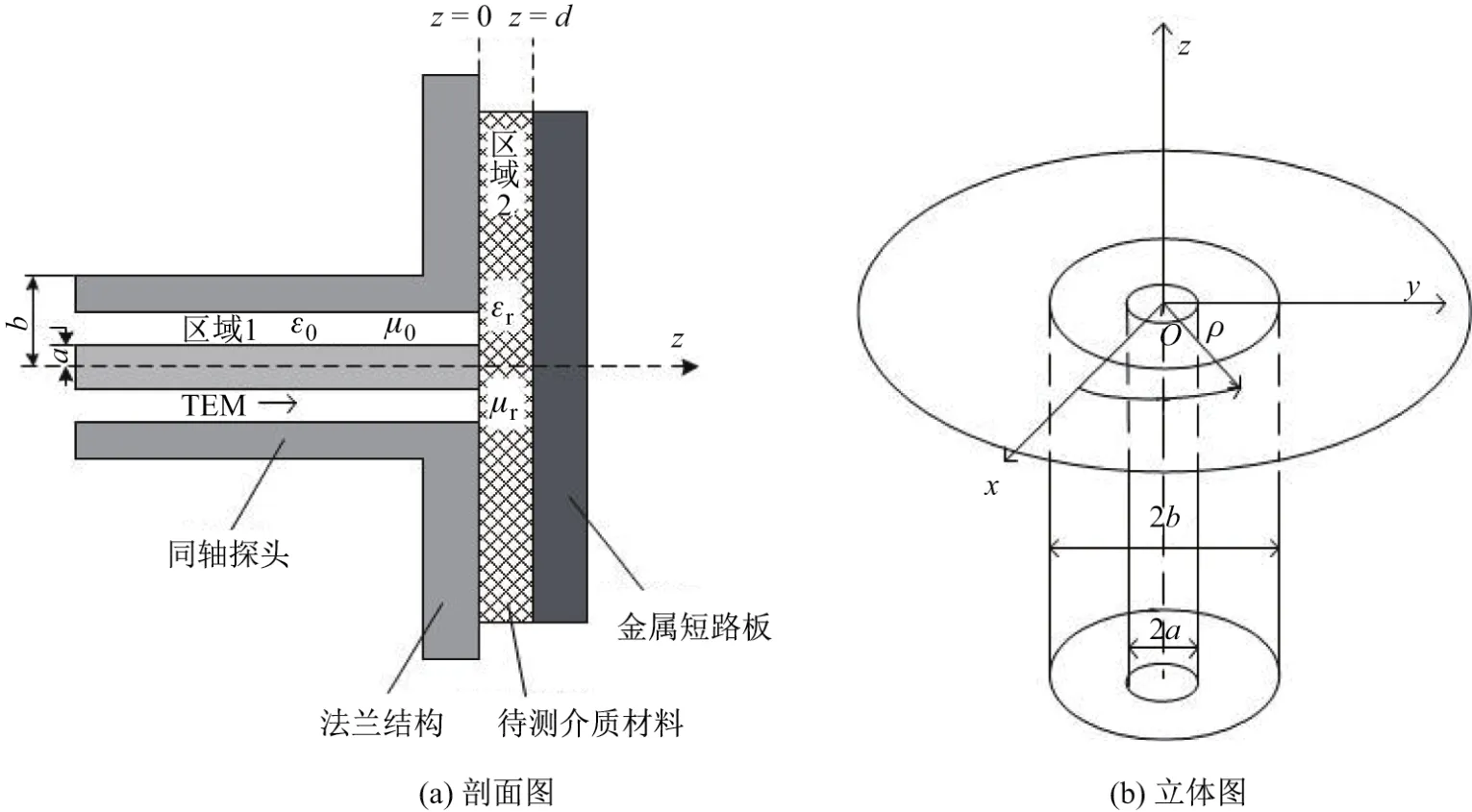
图1 同轴探头测量吸波介质电磁参数示意图Fig.1 Geometry of an open-ended coaxial probe with f l ange
式中,A0为TEM模的入射波电场幅度,0,其中ε0和µ0分别为真空的介电常数和磁导率,εc和µc分别为同轴线内填充介质的相对介电常数(忽略损耗)和相对磁导率;Γ0为同轴探头TEM模的反射系数.
根据Hankel积分变换,待测材料中的电磁场可以表示为谱域中所有不同轴向传播常数柱面波的迭加:

在z=0的口径面上,根据电场和磁场横向分量连续的边界条件,由式(1)~(3)可得

为了得到反射系数的计算公式,对式(5)进行适当处理,根据Fourier-Bessel积分公式


将式(7)代入式(5),可得到准静态模式下的归一化导纳

由于短路金属板上(z=d)电场横向分量为0,则有

由式(9)求得

因此得到准静态模式下的归一化导纳为

可得反射系数理论计算值为

从上述推导得到的准静态谱域模型的导纳计算公式可以看出,该公式为一重积分,积分区间为(0,∞),因此由式(11)计算得到的理论计算值存在一个数值积分截断误差,通过实验对比发现,此误差主要来自对积分上限∞的近似及数值积分.在考虑数值收敛和计算难度的前提下,可先从大范围确定积分上限的值,然后逐步缩小范围至合理的取值.
利用已知的反射系数参考值对积分上限的取值进行验证计算,在验证程序中所采用的同轴线内外半径分别为a=0.5 mm和b=1.67 mm.作为参考的已知材料为胶木板,其相对复介电常数为5.5−0.5j,相对磁导率为1.经程序验算(见图2)可知,取得点数过少会导致积分收敛不够以及计算结果误差较大,如取上限为1 000时.通过反复验算,当取上限分别为10 000和6 000时,发现由式(11)计算得到的反射系数值与参考值较一致,经计算验证最终取积分上限值为3 000即可.当被积函数的分母为0时,此积分无意义,参照前述方法验证,只有当下限值x大于200时才会出现较大的偏差,因此当x的积分下限低于一定取值时,对积分结果的影响满足所能容许的误差范围,计算结果与参考值基本保持一致.
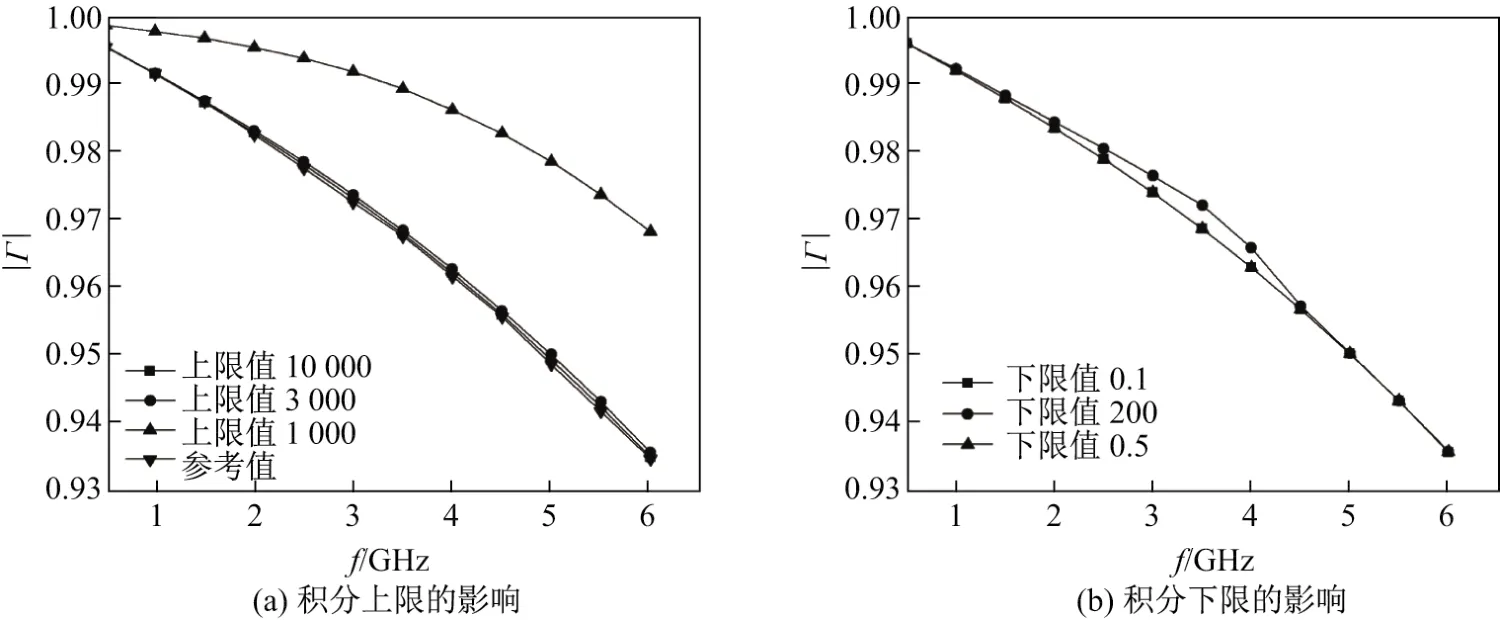
图2 被积函数上下限取值Fig.2 Values of upper and lower limits of integrand function
2 优化反演计算方法
2.1 计算原理
图3显示了整个测量计算技术的详细过程[11],大致可以分为如下三步:一是测量;二是数值公式的理论计算;三是优化迭代反演计算.将开口同轴探头和矢量网络分析仪的单端口相连接,测量得到待测材料的反射系数Γm,利用上述推导得到的式(12),通过程序计算得到反射系数的计算理论值Γc;然后建立优化迭代所需要的误差函数,即

这是一个求方程极小值的问题,在优化过程中采用局部优化方法,在编程优化时运用Matlab中的fminsearch函数,此函数在给定初值的情况下,找到一个二维曲线的最小值,也是局部最小值,此时对应的变量值则作为目标优化值.在给定误差范围的条件下,通过不断迭代反演可以确定材料的电磁参数,达到了测量介质电磁参数的目的.

图3 介电常数反演算法Fig.3 Inverse algorithm of permittivity
2.2 数据拟合
使用网络矢量分析仪采用传统的开路-短路-匹配法进行校准,在扫频条件下测得的反射系数曲线并不是随着频率的变化而缓变、平滑的,与此相反,测得的曲线是剧烈振荡的、不光滑的.产生这种结果的原因是由于测量中的校准误差,主要是“残余适配误差”[12-14],即由于校准精度所限而存在的残余误差,反映到测量的参数结果就是曲线上会有毛刺.
针对这种情况,本工作采用数据拟合技术对测得的反射系数进行处理.如图4所示,通过矢量网络分析仪直接测得的结果为虚线,反射系数的实部曲线随着频率跳变离散,而采用数据拟合后的曲线是一条随着频率缓变的平滑曲线.根据多项式次数选取遵循的原则如下:尽量使拟合曲线处于测量值曲线的中央,次数过多会引入拟入误差,次数太少则会使拟合后的反射系数曲线跟不上频率的变化,与测量值曲线相差过大;由于离散测量值所取的点越多,所包含的反射系数随频率变化的信息越多,在满足拟合曲线随频率变化的前提下,拟合的点越多越好,这样拟合曲线才能更精确地代表原测量值曲线,从而减小误差.通过2次多项式和4次多项式数据拟合结果的对比可知,用2次多项式拟合的结果曲线随频率的变化与原测量值曲线一致,尤其从初始阶段2 GHz处,2次多项式拟合的数据曲线采样点与原测量所得数据的采样点吻合得更好,而且从数据整体变化趋势来说,2次多项式拟合的点数效果优于4次多项式拟合效果.因此,本工作最终采用2次多项式拟合次数.

图4 不同数据拟合次数的结果比较Fig.4 Comparative results of dif f erent data f i tting numbers
2.3 多值解分析
在测量复电磁参数时,“多值解”始终是一个需要解决的问题.在工程上,遇到的多值解问题可以分为两类:一类是由于建立的物理模型在数学求解上存在多个解;另一类是由于测试精度较低导致计算值存在一个可变的动态范围.相对而言,第二类多值解问题较为常见,而此类问题是与电磁参数测量结果的不确定度密切相关的,是由于对试验参数的提取不当而造成不确定度增大,在这种条件下多值解问题相当严重.本工作采用局部优化迭代方法,通过程序的反复优化迭代,在满足目标函数式(13)的收敛条件的前提下,程序验算得到一个最小值,程序运算结束,所得的相对介电常数计算值则作为待测介质的相对介电常数的近似值.
2.4 误差分析
用开口同轴探头技术测量电磁参数,反射系数的不确定主要来自3个方面的原因,即计算误差、模型误差和测量误差.计算误差包括计算机的计算精度、数值上下积分的取舍精度以及准静态模型所引起的模型误差;模型误差则是由于在实际条件下,用有限大法兰半径和材料半径来近似等效无限大的理论模型所引起的误差;测量误差则是由于无法避免的仪器测试精度和人为测量精度所引起的误差.
相对而言,计算机舍入误差造成的影响可以忽略不计,由2.2节分析可知,通过选择合适的积分上下限,使得计算结果达到了精度要求,本工作所采用的准静态模型带来的模式截断误差符合一定的误差要求.而关于建模误差和测量误差,由于法兰与材料之间的空气间隙会对结果产生较大的影响,故在测量时应尽量将法兰紧贴材料表面,材料应尽可能光滑平整,以达到减小误差的目的.由于实际测量所使用的法兰、待测材料以及短路金属板的半径都是有限尺寸的,与理论谱域模型中的无限大半径尺寸不一致,因此也必然会引入误差.文献[15]对于同轴探头加载单层高损耗介质样品进行了研究,通过分析验证给出了有限法兰可视为无限大法兰的前提条件:Rf−b>3λg,其中Rf为法兰半径,b为同轴探头外半径,λg为介质中的波长.
3 测量结果
为了验证本工作提出的测量技术的可行性,使用网络矢量分析仪采用开路-短路-匹配法校准,在2~18 GHz频段内测量加载在开口同轴探头末端介质材料的复反射系数.测量所使用的同轴探头内外半径分别为a=1.5 mm和b=3.5 mm,法兰直径为d=60 mm.为了减小测量误差,在网络矢量分析仪可以分辨相邻频点的前提下,测量应选择尽量小的频率间隔,本工作测量所采用的频率间隔为11.25 MHz.由于测量仪器采用的校准方法会产生残余适配误差,因此用矢量网络分析仪测得的数据会产生毛刺现象,通过2~9次多项式拟合比较,最终采用2次多项式拟合处理.
由图5的结果可知,由反射系数式(12)计算得到的结果与用矢量网络分析仪测得的结果变化一致,其中理论计算的反射系数值和矢量反射计测得的反射系数值的实部基本吻合,变化趋势一致,结果较为准确;而虚部在高频区域总体变化趋势一致.在2~18 GHz区域出现部分偏差的原因主要由以下三部分组成:一是采取的准静态模型忽略了高次模对计算误差的影响;二是不可避免的系统校准误差;三是人为测量引起的误差.
根据程序验证,对低损耗介质聚酯薄膜进行了测量计算.选择的验证样品是厚度均为0.1 mm的聚酯薄膜,总共测试验证了20层.从图6中的数据可以看出,相对介电常数的实部和虚部的表现都很稳定,随着层数的增加,即在增加了厚度的情况下,测试得到的相对介电常数实部和虚部一致性较好,由此测出的相对介电常数为2.2−j10−6.从实验验证的角度看,本方法可用于片状介质材料相对介电常数的测量.在一定的现场测量条件下,以上测量结果是可信的,说明测量方法是可行的.

图5 样品的测量计算结果Fig.5 Measured and computed results of sample

图6 聚酯薄膜测量结果Fig.6 Measured results of polyester f i lms
4 结束语
本工作在推导的谱域模型的基础上,运用终端短路开口同轴探头测量技术对具体样品进行测量.利用优化迭代反演计算出介质材料的相对介电参数,反射系数理论值和测量值的结果比较进一步验证了所提出优化迭代反演算法的可行性.本工作提出的测量优化方法适用于快速测量片状损耗介质材料,对于低损耗材料的测量误差相对较大,因此未来将进一步探究如何提高对低损耗介质材料测量的精准度.
[1]STUCHLY M A,STUCHLY S S.Coaxial line ref l ection methods for measuring dielectric properties of biological substance at radio and microwave frequencies—a review[J].IEEE Trans Instrum Meas,1980,29(3):176-183.
[2]STUCHLY M A,ATHEY T W,SAMARAS G M,et al.Measurement of radio frequency permittivity of biological tissues with an open-ended coaxial line:partⅡ—experimental results[J].IEEE Transactions on Microwave Theory and Techniques,1982,30(1):87-92.
[3]XU D M,CHEN C P,NIU M D.Recent advance on open-ended coaxial probe measurement techniques[C]//APMC Proceeding.2002:999-1006.
[4]CHEN C P,XU D M,NIU M D,et al.Further study on in-situ measurement of complex EM parameters with a f l anged open-ended coaxial probe[J].IEEE MTT-S International Microwave Symposium Digest,2004,2:1221-1224.
[5]DIjANA P,LEAH M,CYNTHIA B,et al.Precision open-ended coxial probes for in vivo and ex vivo dielectric spectroscopy of biological tissues at microwave frequencies[J].IEEE Transactions on Microwave Theory and Techniques,2005,53(5):13-22.
[6]PARk S,LEE J,CHEON C,et al.A new simultaneous measuring method of complex permittivity and permeability using two-port probe[C]//IEEE MTT-S International Microwave Symposium.2007:527-530.
[7]SHARMA A,AFSAR M N.Accurate permittivity and permeability measurement of composite broadband absorbers at microwave frequencies[C]//Instrument and Measurement Technology Conference.2011:1-6.
[8]HASSAN A A.Multilayer medium technique for nondestructive EM-properties measurement of radar absorbing materials using f l anged rectangular waveguide sensor and FDTD method[C]//IEEE International Symposium on Innovations in Intelligent Systems and Applications.2014:68-75.
[9]LI C L,CHEN K M.Determination of electromagnetic properties of materials using f l anged open-ended coaxial probe full wave analysis[J].IEEE Trans Instrum Meas,1995,44(1):19-27.[10]JARvIS J B,JANEZIC M D,DOMICH P D,et al.Analysis of an open-ended coaxial probe with lift-of ffor nondestructive testing[J].IEEE Trans Instrum Meas,1994,43:711-718.
[11]WANG S J,NIU M D,XU D M.A frequency-varying method for simulataneous measurement of complex permittivity and permeability with an open-ended coaxial probe[J].IEEE Transactions on Microwave Theory and Techniques,1998,46(12):2145-2147.
[12]STUCHLY M A,STUCHLY S.Coaxial line ref l ection methods for measuring dielectric properties of biological materials at radio and microwave frequencies:a review[J].IEEE Trans Instrum Meas,1980,29(3):176-183.
[13]HASSAN A A.Error analysis of rectangular waveguide probe with f i nite f l anged for nondestructive EM-properties and thickness measurement[C]//IEEE International Symposium on Innovations in Intelligent Systems and Applications.2013:1-4.
[14]CHEN C P,CHEN M Y,YU J P,et al.Uncertainty analysis for the simultaneous measurement of comlpex electromagnetic parameters using an open-ended coaxial probe[C]//Proceedings of the 21st IEEE Instrumentation and Measurement Technology Conference.2004:61-65.
[15]HASSAN A A,WANG R,XU D M,et al.Numerical analysis of open-ended coaxial probe with fi nite ground plane for nondestructive electromagnetic properties and thickness measurement[C]//ICEMI’99.1999:18-21.
Optimal computation and measurement of permittivity of f l ake dielectric materials
ZHOU Jianjun,ZHANG Ning, YAN Jinkui
(School of Communication and Information Engineering,Shanghai University,Shanghai 200444,China)
Based on an open-ended f l anged coaxial probe technique,this paper measures complex permittivity of f l ake dielectric materials loading at the end of a probe.The method compares measured values and theoretically calculated values,the measured values being processed by optimization iteration computation.This paper introduces a theoretical model and the measurement system in detail.Feasibility and rationality of the presented method are shown by measuring some common materials.
open-ended coaxial probe;complex ref l ection coefficient;relative dielectric constant;optimization iterations method
O 441.5
A
1007-2861(2017)05-0674-08
10.12066/j.issn.1007-2861.1673
2015-10-19
上海市重点学科建设资助项目(S30108);上海市委重点实验室资助项目(08DZ2231100)
颜锦奎(1965—),男,副教授,博士,研究方向为微波介质测量.E-mail:jkyan@shu.edu.cn

