萤火虫模型在水下传感器网络时间同步中的新应用
金彦亮,方昌立,张晓帅,姚 彬
萤火虫模型在水下传感器网络时间同步中的新应用
金彦亮,方昌立,张晓帅,姚 彬
(上海大学通信与信息工程学院,上海200444)
时间同步是传感器网络的基本需求,但在复杂的水下环境中,水下无线传感器网络(underwater wireless sensor networks,UWSNs)的时间同步面临着两大挑战:长传播时延和节点的移动性.将萤火虫同步算法模型应用于水下,提出了水下萤火虫算法机制,利用其良好的相位补偿特点,结合新的动态分簇机制,有效地提高了同步效率,缩短了同步时间.同时,巧妙结合Chirp扩频信号具有较强抗多普勒能力的特点,进一步提高了水下无线传感器网络的同步精度.通过仿真实验,验证了水下萤火虫同步算法的优异性能.
水下无线传感器网络;萤火虫模型;Chirp信号;时间同步;多普勒效应
水下无线传感器网络(underwater wireless sensor networks,UWSNs)的时间同步在海洋军事网络系统、生态采集系统、监测航道运输系统、勘测海底能源等领域有着广泛的应用[1].许多学者提出了一些具有较高精确度的水下时间同步算法.早期有考虑水下广播机制和节点移动性的TSHL[2]和MU-Sync[3]算法,后来进一步发展出把多普勒因素也考虑到水下环境中的D-Sync[4]和Mobi-Sync[5]算法.本工作首次将萤火虫同步算法模型应用于水下无线传感器网络,根据其分布式和相位补偿特点,提出新的动态分簇机制,以优化和缩短网络系统的同步时间.同时,由于水下节点具有移动性,节点间会存在多普勒效应,为了更好地估计长传播时延,本工作创新地设计出结合Chirp信号的物理帧结构,利用Chirp扩频技术克服水下多普勒效应,以获取更高的同步精度.
1 相关工作
1.1 萤火虫同步算法模型
首先,介绍经典的萤火虫算法的M&S模型和RFA(reachback f i ref l y algorithm)模型.然后,在此基础上为了克服水下多普勒效应及信道衰减而引入Chirp扩频技术,较好地解决了水下传感器网络面临的长传播时延和节点移动性问题.
1.1.1 M&S模型及RFA模型

1990年,Mirollo等[6]提出一种实用的脉冲耦合振荡器模型——M&S模型,该模型奠定了萤火虫算法的基础.在此模型中,振荡器依然使用状态变量x来描述,x的变化服从函数f(φ)(相位-状态方程),其中f是[0,0]到[0,1]上的平滑单调递增凸函数:式中,b是消散因子且b>0,它和曲线的弯曲程度成正比.当b→0时,f(φ)=φ(线性相位-状态方程),φ是相位变量且满足dφ/dt=1/T(T是同步周期).尽管M&S模型完美证明了全连通网络中耦合脉冲对的同步可能性,但是该模型的缺点是所有的振荡器有相同的晶振频率,且网络必须是全连接的,耦合过程节点间的时延忽略不计.
针对这些局限性,Tyrrell等[7]给出了RFA模型.相比于M&S模型,RFA模型在本轮同步周期中节点的相位不受同步报文的影响,还较好地解决了报文传输延时问题.图1可以反映出这两个同步模型间的差别.

图1 M&S和RFA同步模型Fig.1 M&S and RFA synchronization model
在图1(a)中,当节点监听到邻居节点激发时会及时增加自身增量;在图1(b)中,节点在监听到邻居节点激发后并没有立刻作出反馈,而是把下一轮的节点起始时间设置成上个周期积累的相位增量和.这些特点都为RFA模型应用于水下传感器网络创造了条件.
1.1.2 同步时域不应期
在萤火虫模型中,为了解决当时延存在时出现的“回声”现象,可以使耦合脉冲对在一定时间段内对收到的同步信息不作回应,这个时间段称为不应期,其大小应满足

式中,maxvij是节点网络中相距最远的节点传输信号的延时,而两倍的最大延时表示一个同步信号从发射点到原点的往返延时,不应期时间内须忽略掉该时间内接到任意同步信号作用.根据RFA萤火虫同步算法相位补偿优势及同步时域不应期的特点,可将其应用于水下所需解决的同步问题.考虑到本工作中节点都是动态的,需要研究移动节点间的多普勒效应的影响,故引入了Chirp扩频技术.
1.2 Chirp信号
Chirp信号也可称作线性调频信号(正弦信号),在一定时间内其频率随时间线性增大或减小.由于Chirp扩频具有较大时间带宽积,抗多普勒性能较好,因此可以利用多普勒效应来减小同步误差.Chirp信号表达式如下:

式中,f0为信号中心频率,rect(t/T)为矩形窗函数,

因为Chirp信号具有很尖的脉冲并且容易被检测到,所以可以在一个噪声信道里面被捕获到.根据这个特点,在水下复杂环境中设计出结合Chirp信号的水下萤火虫同步算法数据帧结构,能够得到更加可靠的数据报文,以更加精确的方式来估计多普勒因子,计算出长传播时延.
1.3 时钟相位和时钟频偏
时钟模型是用来进行时间同步协议性能失效性分析的常用数学模型.定义传感器节点i在某个物理时刻t的本地时间为

式中,ai和bi分别为节点i的时钟偏移和时钟频偏,每个节点都有一个起始时间并形成一个时钟模型.时钟偏移和时钟频偏是导致同步误差的主要因素,而时钟偏移会引起独立于时间的常数误差,然而时钟相位则会导致随时间而增加的误差.为了得到较好的同步性能,要同时考虑这两个因素.
2 水下萤火虫同步算法模型
水下萤火虫算法模型是一个跨层的时间同步研究方法.根据萤火虫算法具有的分布式和RFA模型的相位补偿特性,本工作提出水下萤火虫动态分簇新机制,从物理层提出快速实现簇内和簇间同步的方法,同时可以较好地解决报文的传输时延问题,以获取更加可靠的报文数据来计算长传播时延.在设计物理帧结构时,巧妙结合Chirp扩频信号,提出用分段多普勒估计方法来估计多普勒规模因子;然后在应用层,利用从物理层获取的时间戳信息,结合估算出来的多普勒规模因子,通过数学处理可以计算出传播时延.
2.1 水下萤火虫动态分簇机制
水下萤火虫同步模型如图2所示,海平面上有信标节点,水下有很多无线传感器网络节点,图中红色的圆圈表示信标节点,可以获取来自水面接收站从同步卫星传过来的GPS授时,蓝色的圆圈表示普通待同步节点.

图2 水下萤火虫同步模型Fig.2 Model of underwater f i ref l y synchronization
Sun等[8]提出的无线传感器网络的分簇策略是基于相位排序实现完全的等间距分簇.这种依据间隔的分簇方式可以达到较好的同步效果,但为了实现更快速的同步,本工作提出了一种基于邻近相位的快速排序方法.本工作动态分簇的核心思想是:在一定的节点范围内,以最快的速度实现同步为出发点,把节点按照相位最相近的原则分到一个簇,然后依次划分出若干个簇.相位越近,需要调整的间隙越小,簇内相位调节以实现同步的速度越快,时间越短.从理论上可以完成上述相位分簇,针对实际中存在相近相位也不一定在邻近范围的情况,可以按照一定的概率原则,每簇选取尽可能相近的相位,但不排除在每簇中存在个别相位差异较大的节点.此处假设所有的节点均可参与同步,网络为全连通的,暂不考虑节点在同步过程中出现失效以及毁坏的情形.
假设网络中每个节点i均为相同的脉冲振荡器,每个节点触发Firing时间的频率为ω,周期长度为T=1/ω.在标准化处理各个节点之后,用ψi(t)来表示节点当前的一个状态,即状态函数ψi(t)为每个节点的相位,且满足ψi(t)∈θ,θ=[0,1],1≤i≤K,每个节点在T时间内从0匀速增加到1,其增长率为dψi(t)/dt=1/T.当某一时间t0≥0满足
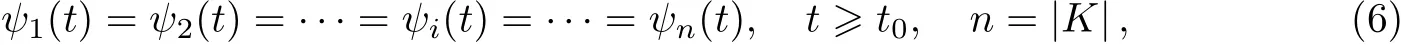
则认为网络达到了同步状态.
2.1.1 簇内同步
在分簇前,需要初始化网络中的参数,节点数K=n,周期时长为T0,系统随机分配初始相位,定义Q为相位从0到阈值的最大度量.
初始化各节点的相位后按大小进行排序:

再根据最大、最小相位的差值得出最大相位差

可以推导出分簇的数目

接下来是最重要的部分,即把最相近的相位节点分在同一簇中,然后按照这个规则依次划分.首先把网络中相位最小的一组标记为第一簇,然后倒数第二小的标记为第二簇,依次排列出N簇,每一簇的节点数目为n/N:
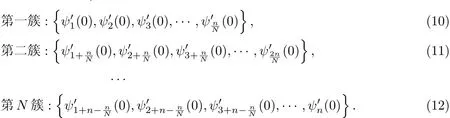
这样分簇后,簇内节点的相位在较小的差异下,依据RFA同步模型进行最优化分簇,各节点只与本簇节点产生信息交换,依据萤火虫同步节点的平级特点,所有簇内节点均被视为“簇头”.这样能更快地实现簇内同步,更好地满足水下传感器网络的同步要求.
2.1.2 簇间同步
因为簇间同步需要一段时间,网络系统会设置一个合适的等待时间,以保证簇的同步完全完成.依照RFA同步模型规律,此时网络是由一些异步节点逐步调整成N个独立的节点.随后这N个独立节点相互耦合相互影响,最后完成簇间的同步.簇间同步机制的详细过程将在2.3节结合水下萤火虫公式进行分析.
2.2 多普勒规模因子估计
为了估计多普勒规模因子,已有学者提出模糊度函数法[9],但是这种方法的最大缺点是需要大量的自相关器,从而导致较大的运算量和硬件复杂度.本工作引入一种更加实用且有效的方法,称为分段多普勒估计法.图3为本工作提出的分段帧结构,在该帧结构中,传输的萤火虫同步信号是由两个线性调频(linear modulated frequency,LMF)的Chirp信号结合在一起,中间两段空白作为保护间隔.

图3 结合LMF Chirp信号的帧结构Fig.3 Frame structure combining LMF Chirp signal
根据Chirp同步信号的特点,本工作采用匹配滤波器法检测同步信号,其流程如图4所示.首先对时间窗内截取的同步信号进行匹配滤波,检测匹配输出信号的峰值,然后获取输出信号的峰值点位置,根据峰值点位置的偏移量计算信号的同步时刻.

图4 Chirp信号匹配相关的同步信号检测流程图Fig.4 Matching related detection f l ow chart of synchronization signal of Chirp signal
定义传输输入信号数据包的时间为Γtp,当匹配滤波器接收到数据时,可以测量出位置偏移量为Γrp,也就是接收一个数据帧的过程,

式中,ϑ为多普勒规模因子.这样就能精确得到多普勒规模因子的数值,从而获得节点间的相对移动速度.在不同的水下环境里,水声速度是一个变化的值.影响水声速度的因素有很多,比如海水的温度、深度、盐度以及水压.本工作把水声传播的速度认为是常量C=1 500 m/s,根据对应的物理关系,节点相对速度的估计公式为

在真实的水下环境中,节点在往返程的多普勒影响是不同的,这也导致节点间往返程的相对速度也是不同的.根据本工作的信息机制,可以推导出

式中,ϑ1,ϑ2分别代表去程和回程的多普勒规模因子的大小,υ1,υ2分别代表去程和回程节点的相对估计速度.
2.3 同步信息交换机制
在时间同步研究领域里,有许多典型的信息交换机制,例如单发送方式、发送-接收方式以及接收-接收方式等.泛洪时钟同步协议(f l ooding time synchronization protocol,FTSP)[10]是典型的单发送方式,该机制能量消耗大,同步精度也不够;参考广播同步(reference broadcast synchronization,RBS)[11]协议,Mobi-Sync和D-Sync均采用发送-接收方式,这种方式的时间同步精度较高.本工作信息交换机制采用发送-接收机制(见图5),以获取较高的同步精度.
选取某一个簇内的两个节点,A为参考节点,可以获取来自水面接收站传送的标准时间,B为普通待同步节点.参考节点A广播其带有时间戳TA1[1]的信息给邻近节点B,节点B在TA1[1]+γ[1]接收到参考信息,经过处理后,节点B将回传带有时间戳TB2[1]的信息给参考节点.两节点间进行物理层的相位补偿,经过多次信息交换,按照本工作提出的水下萤火虫动态分簇机制最终达到整个簇内的同步.
但是,水下的节点并不是固定不变的,会随着洋流以及其他因素发生位置变化.这里假设两个节点在一维的直线上,无论节点是相互靠近还是远离都是可计算的模型.下面介绍假定普通节点远离参考节点的传播时延估计过程.

图5 信息交换机制Fig.5 Message exchange scheme
选取第一个信息交换回程:TA1[1]→TB1[1]→TB2[1]→TA2[1].首先定义:

式中,Δγ为往返传播时延的差值.根据信息交换机制可以推导出
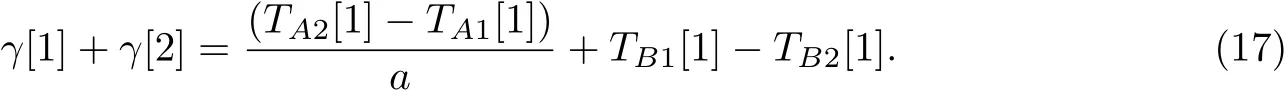
在本工作提出的水下萤火虫同步模型中,假定普通节点和参考节点的相对速度是线性增长的.Δd表示从TB1[1]到TA2[1]的相对距离,可以估计出

考虑到整个时间同步过程,假定Δl为从TA1[1]到TA2[1]的相对距离.更进一步可以得到

同时可以用运动学方程来建立等式:

为了简化计算,忽略传播时延γ2[1],并作如下数学处理:

再结合式(17),(18),(20)和(21),可以分别计算出传播时延γ[1]和γ[2]:

至此,已经推导出传播时延的计算公式.依据上述簇间同步的RFA模型,定义脉冲发射时间为τsend,接收到的本地时间为τreceive,状态方程需满足

式(24)中,Tp[i]为节点间传播时延,T为同步周期长度,由于γ[i]=Tp[i],a=φsend,依据式(22)和(23),可以建立等式分别求出传播时延γ[1],γ[2].反代入式(24),(25)和(26)可求出节点相应的相位状态φsend.
此处求解传播时延的方案不同于传统的线性拟合,传统方案是通过一组数据进行线性回归处理来估计传播时延,这就需要采集大量的数据才能满足必要的同步需求,同时在线性回归处理时,也是通过近似方法来实现的,进一步带来了误差.而本工作则运用萤火虫同步算法模型的特点,与所提出的多普勒估计方法巧妙结合直接求出变量,具有更高的准确性,并减少了同步误差.
3 仿真
本工作提出的水下萤火虫同步算法中的误差主要来源于以下两个方面:一是带有Chirp信号的参考节点从开始发送信息到接收的整个过程所受到的多普勒频移,导致两个自相关的主峰之间产生时滞,误差近似为

二是节点在相互的信息交换机制间的误差,这主要是由于在萤火虫同步期间信道随机噪声带来的影响.本工作近似地把噪声ξ看作是高斯随机误差,得到的总的同步误差表达式如下:
对于水下传感器网络同步而言,最大的挑战是如何减少算法的同步误差.为了更加科学地研究水下萤火虫模型并验证其准确性,本工作进行了1 000次的仿真实验获取平均值.根据水下环境的特点,本工作首先选取了合适的仿真参数(见表1).
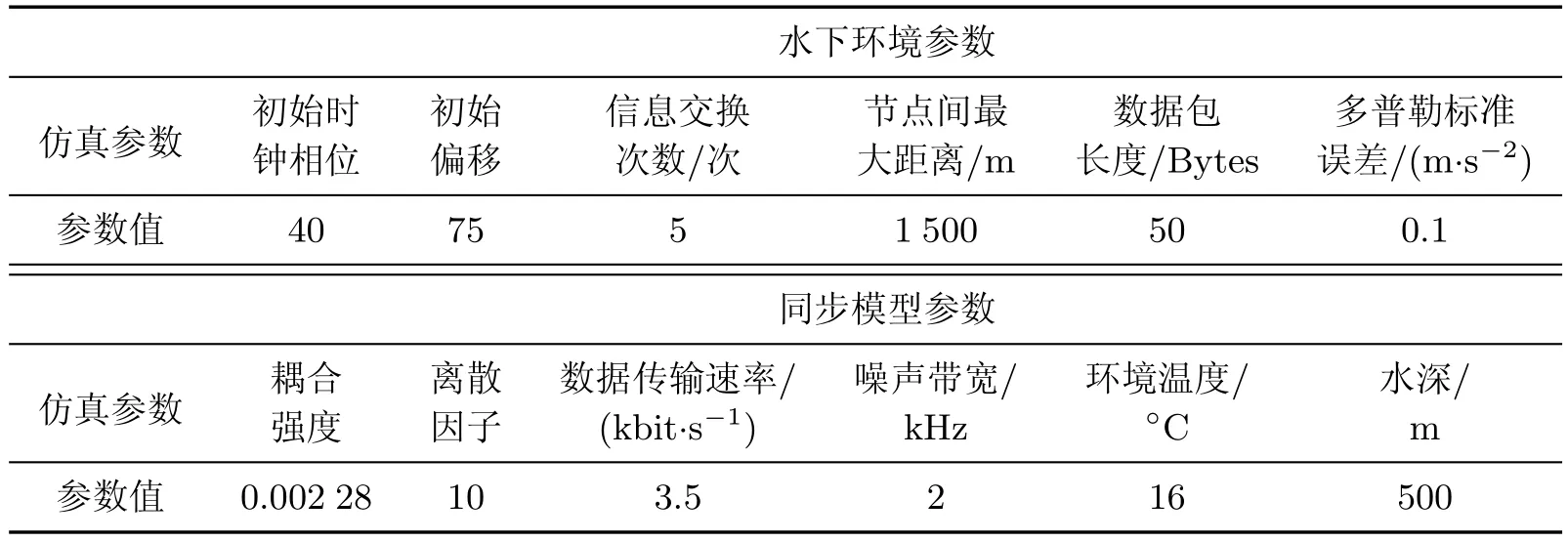
表1 水下萤火虫同步算法仿真参数Table 1 Simulation parameters of the underwater f i ref l y synchronization algorithm
首先研究经典的同步算法和水下萤火虫同步算法同步速度的关系.如图6所示,在仿真中对同步时间进行归一化处理,得出时间同步关系.可以看出,水下萤火虫同步算法最先达到同步.D-Sync和Mobi-Sync的同步速度大体相当,而TSHL(time synchronization for high latency)算法则表现出较差的同步性能,基本上在其他的同步算法达到同步很长一段时间内才逐步达到同步.这是由于水下萤火虫模型动态分簇新机制的良好特性能够更快地实现同步,而TSHL节点不具有动态特性,更没有考虑多普勒效应的影响,因此导致同步性能最差.

图6 几种算法同步时间比较Fig.6 Comparison of several algorithms for synchronization time
接着比较几种典型的水下同步算法在水下萤火虫环境下的性能.同样经过多次大量的仿真,求取平均值,可得如图7所示结果.从图7中的总体趋势可以看出,达到同步后随着同步时间的增加,所有同步机制的同步误差都在变大,几乎是以指数趋势增长.Mobi-Sync的性能明显要优于TSHL,实际上通过仿真可以得出,TSHL在水下环境中的性能表现甚至比没有同步的情况都要差,主要原因是TSHL节点是静止的,传播时延也是按照常数来计算的,这样必然导致估计时钟相位非常不准确.D-Sync的性能要优于Mobi-Sync,Mobi-Sync算法尽管详细考虑了节点的移动性问题,但是却忽略了水下多普勒因素对移动节点具有较大影响;D-Sync算法是基于多普勒的时间同步算法,有较大的克服多普勒效应的能力.而本工作提出的水下萤火虫同步算法结合Chirp信号的物理层结构,更好地克服了多普勒效应;同时利用萤火虫模型良好的相位补偿优势,使得同步后的误差维持在一个非常低的水平,最终获得了非常好的同步性能.
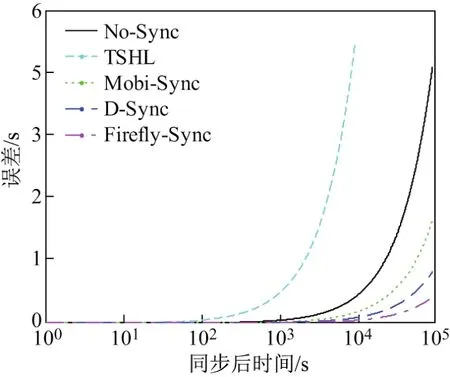
图7 同步后时间与同步误差的关系Fig.7 Time vs.error after synchronization
从图8中可以明显看出,动态分簇新机制对同步时间起重要作用.在具有动态分簇新机制和不具有动态分簇两种情况下,动态分簇使同步速度得到非常大的提升,可见动态分簇新机制对于改善水下传感器网络的时间同步速度具有重大意义.

图8 动态分簇新机制和非动态分簇机制对比Fig.8 Dynamic clustering machanism vs.non-dynamic clustering machanism
由于上述仿真均在5次信息交换下得出结果,显然同步信息交换的次数对于同步误差也有很大的影响.下面进行了在不同信息交换次数下的仿真,验证同步误差随着同步信息交换次数增加的变化(见图9).可以看出,随着信息交换次数的增加,同步误差逐步减小,这也符合实际情况.当一个同步周期内信息交换次数增加了,必然是相位不断得到调整,从而使得同步误差处于较低的水平.而对于没有时间同步的情况,随着时间的增加,必然导致误差的积累,由仿真结果可知,同步误差趋势呈近似线性增长.
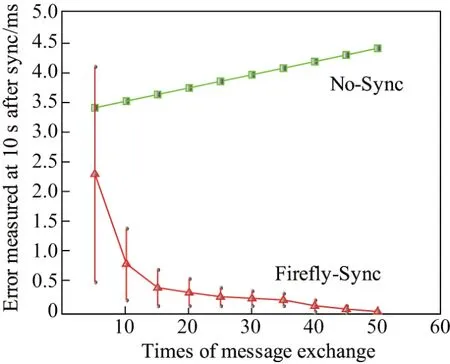
图9 信息交换次数与同步误差关系Fig.9 Message exchange times vs.synchoronization error
4 总结与展望
本工作是将萤火虫算法模型应用到水下传感器网络时间同步中.为了更好地将萤火虫算法应用于水下,发挥其良好的相位补偿优势,首先提出了基于动态分簇的新机制,以最相近的相位划分为簇的原则,极大地提高了同步速度;然后针对水下移动节点存在的多普勒效应,巧妙提出了结合Chirp扩频技术的方法,设计出可以克服多普勒效应的物理帧结构;再利用分段多普勒估计方法以及RFA同步模型,计算出传播时延和其对应的相位状态.同时,本工作较好地解决了水下传感器网络中的同步模型簇内同步和簇间异步的问题,在萤火虫同步模型原则下,簇内通过动态分簇完成同步,簇间则通过相互异步的独立节点,在Firing的影响下逐步实现簇间的同步,最终达到整个网络的同步.
但是影响水下环境的时间同步有诸多因素,本工作仅从节点的动态性以及多普勒效应角度去考虑同步问题,另外水下环境中还存在严重的多径效应、信道衰落等方面问题,下一步本工作将重点关注这些影响因素.
[1]钟海东,邬春学,孔若英.无线传感器网络时间同步算法误差分析[J].微计算机信息,2008,24(4):157-158.
[2]SYED A A,HEIDEMANN J S.Time synchronization for high latency acoustic networks[C]//INFOCOM.2006.
[3]CHIRDCHOO N,SOH W S,CHUA K C.MU-Sync:a time synchronization protocol for underwater mobile networks[C]//Proceedings of the Third ACM International Workshop on Underwater Networks.2008:35-42.
[4]LU F,MIRZA D,SCHURGERS C.D-sync:doppler-based time synchronization for mobile underwater sensor networks[C]//Proceedings of the Fifth ACM International Workshop on Under-water Networks.2010:3.
[5]LIU J,ZHOU Z,PENG Z,et al.Mobi-Sync:efficient time synchronization for mobile underwater sensor networks[J].IEEE Trans Parall Distr Syst,2013,24(2):406-416.
[6]MIROLLO R E,STROGATZ S H.Synchronization of pulse-coupled biological oscillators[J].SIAM Journal on Applied Mathematics,1990,50(6):1645-1662.
[7]TYRRELL A,AUER G,BETTSTETTER C.Firef l ies as role models for synchronization in ad hoc networks[C]//Proceedings of the 1st International Conference on Bio Inspired Models of Network,Information and Computing Systems.2006:4.
[8]SUN Y,JIANG Q,ZHANG K.A clustering scheme for reachback f i ref l y synchronicity in wireless sensor networks[C]//2012 3rd IEEE International Conference on Network Infrastructure and Digital Content.2012.
[9]SHARIF B S,NEASHAM J,HINTON O R,et al.A computationally efficient Doppler compensation system for underwater acoustic communications[J].IEEE Journal of Oceanic Engineering,2000,25(1):52-61.
[10]MAR´OTI M,KUSY B,SIMON G,et al.The f l ooding time synchronization protocol[C]//Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems.2004:39-49.
[11]ELSON J,GIROD L,ESTRIN D.Fine-grained network time synchronization using reference broadcasts[J].ACM SIGOPS Operating Systems Review,2002,36(1):147-163.
New application of f i ref l y synchronization model in time synchronization of underwater wireless sensor networks
JIN Yanliang,FANG Changli,ZHANG Xiaoshuai,YAO Bin
(School of Communication and Information Engineering,Shanghai University,Shanghai 200444,China)
Time synchronization is a basic demand for a sensor network.However,in a complex underwater environment,underwater wireless sensor networks(UWSNs)face two challenges:long propagation delay and mobility of nodes.This paper uses a f i ref l y synchronization model to underwater,and proposes an underwater f i ref l y algorithm.It makes use of good characteristics of distribution and phase compensation to ef f ectively improve the ef f ectiveness of time synchronization and shorten synchronization time.A chirp signal is combined with the model since the chirp has strong of anti-Doppler ability.This also contributes more synchronization precision for underwater wireless sensor networks.Good performance of the underwater f i ref l y algorithm model is verif i ed by simulation.
underwater wireless sensor networks(UWSNs);f i ref l y model;Chirp signal;time synchronization;Doppler ef f ect
TN 301.6
A
1007-2861(2017)05-0647-11
10.12066/j.issn.1007-2861.1765
2015-12-23
上海市科委重点资助项目(12511503303,14511105602,14511105902);上海大学特种光纤与光接入网重点实验室开放课题资助项目(SKLSFO2012-04);上海市教委基金资助项目;上海微系统所无线通信与传感器网络重点实验室开放课题资助项目
金彦亮(1973—),男,副教授,博士,研究方向为无线传感网、移动通信、无线通信等.
E-mail:jinyanliang@staf f.shu.edu.cn
本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn

