Z形薄壁堰过流能力试验

张 靖,常 倩,张庆华,李树宁

(1.山东农业大学水利土木工程学院,山东 泰安 271018; 2.淮河流域管理委员会沂沭泗局河东河道管理局,山东 临沂 276000)

Z形薄壁堰过流能力试验

张 靖1,常 倩2,张庆华1,李树宁1

(1.山东农业大学水利土木工程学院,山东 泰安 271018; 2.淮河流域管理委员会沂沭泗局河东河道管理局,山东 临沂 276000)

鉴于Z形堰的水流特性及过流能力尚未见到相关报道,为研究Z形堰的过流能力,采用概化水工模型,进行了6个堰型方案、12组流量的水工模型试验。结果表明,Z形堰的过流能力大于直线堰,且Z形堰的展宽比越大,流量扩大倍数越大;Z形堰的流量计算可采用通用的堰流公式,其综合流量系数与堰上水深、堰高、展长、前堰宽、后堰宽等因素有关,展宽比、前后堰宽比越大,流量系数越大;堰上水深与堰高之比越大,流量系数越小。利用试验数据给出了考虑堰上水深与堰高之比、展宽比、前后堰宽比等因素的Z形堰流量系数估算公式。

Z形堰;流量系数;展宽比;过流能力;试验研究

堰是水利工程中常见的挡水、泄水建筑物,广泛应用于水闸、溢洪道、河道等工程中。常见的堰有薄壁堰、实用堰和宽顶堰3种基本堰型,其中实用堰、宽顶堰应用最为广泛。在基本堰的基础上,为提高堰的过流能力,并从景观等角度出发,学者们提出了许多新的堰型,如迷宫堰、琴键堰。与传统堰型相比,这些堰型的主要优势包括堰型独特,溢流效果美观,有的过流能力大,特别适用于景观河道工程中挡水、溢流。

20世纪初迷宫堰在低水头的中小型工程中开始应用。20世纪70年代Hay等[1]和Darvas[2]对迷宫堰进行了系统的试验和研究,提出了迷宫堰的设计方法。美国垦务局在Uta坝的设计中,对迷宫堰的水力特性进行了进一步的试验论证,提出了更为实用的设计方法[3]。1984年郭子中[4]将迷宫堰引入到中国并开始研究与应用。2003年法国 Lempérière 等[5]提出了琴键堰溢流堰形式,2006 年在法国西南部的古勒尔坝上建成了世界上首座琴键堰溢洪道,其泄流能力是普通直线实用堰的4倍左右[6]。法国水利工程中心、法国国家水力学与环境试验室对琴键堰开展了大量的研究,印度理工学院,瑞士洛桑联邦理工学院、比利时列日大学、阿尔及利亚 Biska大学、美国犹他州立大学也相继开展了有关琴键堰的研究[7-9],结果表明,琴键堰的堰顶展开长度比、相对水头及进出口宽度比是影响泄流的主要因素,并根据研究结果给出了流量系数的拟合公式。2014年郭新蕾等[10]在搜集试验数据的基础上,提出了琴键堰泄流能力的拟合公式。1997年王仕筠[11]根据系列模型试验资料,提出了不同斜交角度斜交堰流量系数公式,并研究了其水流特性。2006年美国Nguyen[12]对矩形薄壁堰、矩形宽顶堰、堤形堰3种不同形式的45°斜堰的水力特性进行了试验,并对堤形堰分别进行了斜角为0°、45°、60°的物理模型试验。2011年Samuel[13]对薄壁堰、半圆弧堰、1/4圆弧堰3种形式的斜堰进行了试验研究,比较它们的过流能力。2016年黄修筠等[14]通过物理模型试验,对平面为曲线的曲线堰的水力学特性进行研究,得到了堰顶水头随流量的变化关系,计算了2种流量系数。

近年来,在河道工程中基于景观角度考虑出现了一些新的挡水建筑物结构形式。图1所示为青岛市李村河综合治理工程中采用的拦河溢流坝。该拦河溢流坝的形状呈“Z”字形,本文称之为Z形堰。与传统的直线溢流坝相比,这种堰的特点,一是在结构上有前堰、中间堰和后堰,外形呈“Z”字状,堰的整体结构美观;二是水流从前堰、中堰、后堰3处流过,溢流美观,而且由于增加了中间堰,使堰的溢流宽度增大,从而提高了堰的过流能力。因此,其具有较好的应用前景。

图1 某河道Z形堰

Z形堰的水流特性及过流能力目前未见到相关研究报道。为了探讨Z形堰的水力学问题,笔者参考前述迷宫堰、琴键堰等堰型的研究，进行了大量的Z形堰水工模型试验。依据水力学堰流理论,推导Z形堰的流量计算公式,并利用Z形堰水工模型试验数据,对Z形堰流量系数的影响因素进行分析,利用统计分析方法得到Z形堰的流量系数计算公式,供工程设计参考。

1 试验方法

Z形堰由垂直河道的前、后堰和平行河道的中间堰组成,图2为Z形堰平面示意图,图中a为前堰宽度,b为中间堰宽度,c为后堰宽度,d为堰的厚度,W为河道宽度,W=a+c,L为Z形堰的展宽,L=a+b+c,L/W为Z形堰展宽比。

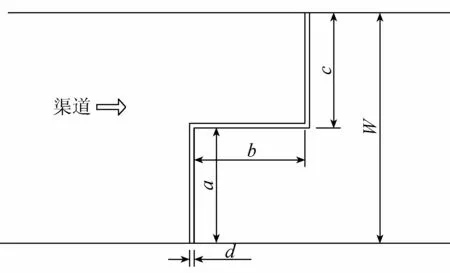
图2 Z形堰平面示意图

1.1 试验模型

试验模型包括上游河道段、Z形堰及下游河道段。河道为矩形断面,宽500 mm,深300 mm。按照试验模型前后堰比值设计了6种试验方案,堰高P=60 mm,堰厚d=10 mm。中间堰的长度可以有多种方案,如果将此作为试验因素,将会使试验方案变得很多,但当前堰与中间堰的长度相同时堰型比较美观,同时为减少试验工作量,本试验仅考虑前堰与中间堰长度相同的情况,即取a=b。试验方案具体参数见表1,其中方案a0为垂直河道的直线堰方案(比较方案),方案a25表示前堰宽25 cm,方案a20表示前堰宽为20 cm,其余类推。

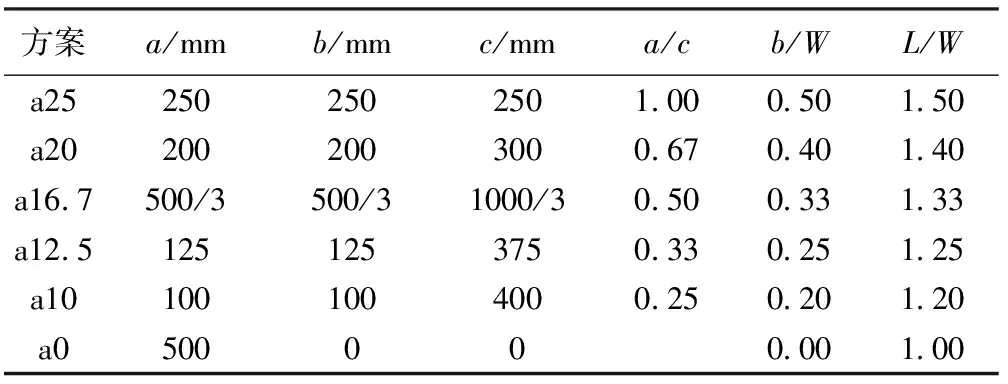
表1 Z形堰试验方案

1.2 试验布置及测量

试验在山东农业大学水利试验室进行。试验系统由地下水库、水泵、高位水池、电磁流量计、闸阀、输水管道、稳流池、模型试验区、回水渠道等部分组成,如图3所示。

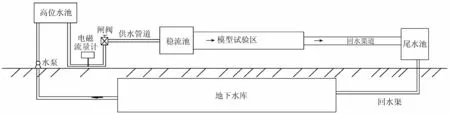
图3 试验系统示意图

首先根据表1分别制作模型,Z形堰材料为PVC塑料板,模型制作完成后,在试验河段模型段进行安装。模型制作、安装严格按照SL 155—2012《水工(常规)模型试验规程》的要求进行。其次进行试验测量。本试验采用定流量、固定断面测量水位及流速的方法。试验时先通过闸阀控制试验需要的流量,待流量稳定后,再进行测试,为了确保试验成果的一致性,每个流量所有测试项目一次完成(中间不允许停水)后再进行其他流量的测量。水深测量在每个位置测量3次,取平均值作为测量结果。流速采用计算机自动采集,采样时间为30 s。

试验主要研究Z形堰的过流能力,主要测量流量、水深和流速,同时观察Z形堰水流情况。在Z形堰前、后均设测量断面,每个断面测量中心线和左右岸边3条垂线的水深、流速,取其平均值为该断面的平均水深、流速。

a. 流量测量与控制。试验通过闸阀控制流量大小,采用开封仪表有限公司生产的E-magC型电磁流量计测量流量。每个模型进行12组测试,流量分别为10 m3/h、20 m3/h、30 m3/h、40 m3/h、50 m3/h、60 m3/h、70 m3/h、80 m3/h、90 m3/h、100 m3/h、110 m3/h、120 m3/h。试验仅研究自由出流条件下的Z形堰过流能力,根据薄壁堰的淹没出流条件,只有当下游水位超过堰顶,且堰后发生淹没水跃时为淹没出流。因此,控制试验流量使Z形堰下游水位不超过堰顶,或堰下游不发生淹没水跃。

b. 水深测量。水深测量采用重庆华正水文仪器有限公司生产的SX40-1型数显水位针,精度为0.01 mm。

c. 流速测量。采用南京瑞迪高新技术公司生产的ZLY-I型智能流速仪。

2 结果与分析

2.1 Z形堰过流分析

2.1.1 过堰流量计算

图4为Z形堰自由出流示意图(图中H为堰上水深,v为堰前断面平均流速)。通过Z形堰的水流分为3部分:一部分从前堰流出,流量为Q1,流速为v11;一部分从中间堰流出,流量为Q2,流速为v12;另一部分从后堰流出,流量为Q3,流速为v13。

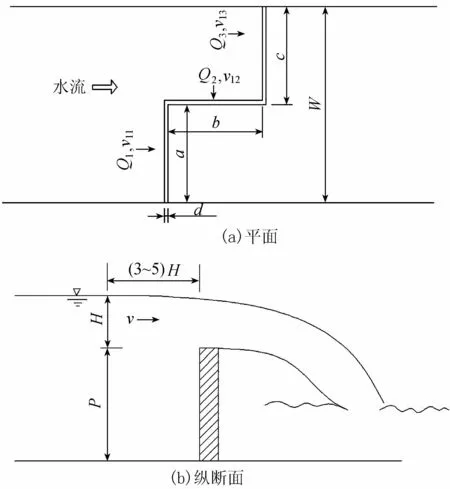
图4 Z形堰过流示意图

通过Z形堰的流量可表示为

Q=Q1+Q2+Q3

(1)

根据堰流理论,在自由出流情况下通过前、中、后堰的流量分别为

(2)

(3)

(4)

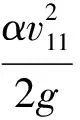
(5)

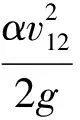
(6)

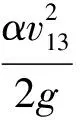
(7)

式中:m1为前堰流量系数;m2为中堰流量系数;m3为后堰流量系数;H01、H1分别为前堰堰上水头、堰上水深;H02、H2分别为中堰堰上水头、堰上水深;H03、H3分别为后堰堰上水头、堰上水深；α为动能修正系数；g为重力加速度。

将式(2)～(7)代入式(1)得

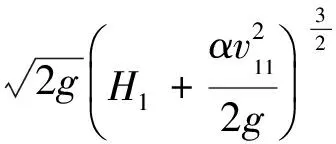
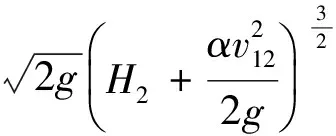
(8)

式(8)虽然完整地表达了Z形堰的流量计算,但是公式形式比较复杂。考虑到流量系数m1、m2、m3难以获得,为尽量简化问题,参照迷宫堰的流量计算方法[15],采用直线堰宽(垂直河道宽度)作为过水断面宽度,且用一个综合流量系数作为衡量Z形堰过流能力的指标;因前堰堰前断面即为Z形堰的堰前断面,因此,以前堰堰上水头、堰上水深作为Z形堰的堰上水头、堰上水深,同时为描述方便用H0、H、v代替H01、H1、v11。由此, Z形堰流量公式(8)可写成一般堰流量计算的表达形式:

(9)

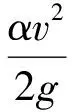
(10)

式中:mw为Z形堰以直线堰宽表示的综合流量系数(以下简称流量系数);W为直线堰宽。式(9)即为以直线堰宽W表示的Z形堰自由出流流量计算公式。

2.1.2 过流能力分析

本试验得到了表1中6种堰型方案不同流量条件下各断面的水深、流速等实测数据。利用试验数据,得到不同展宽比Z形堰实测过堰流量Q与堰前断面水位Hz关系见图5,其中堰前断面水位Hz为图4中距离前堰上游300 mm(约3～5倍堰上水深)断面水深。从图5看到,直线堰的堰前水位点在最上方,即所有Z形堰的堰前水位均比直线堰低,说明在其他条件相同的情况下,Z形堰的过流能力大于直线堰。这是由于Z形堰增加了中间堰,堰宽比直线堰大,因此,增加了堰的过流宽度。另外,从图5还可以看到,Z形堰过堰流量、堰前水位与展宽比L/W有关,在相同流量情况下,L/W越大,堰前水位越低。说明展宽比越大,堰的过流能力越大,该规律与迷宫堰的相同。

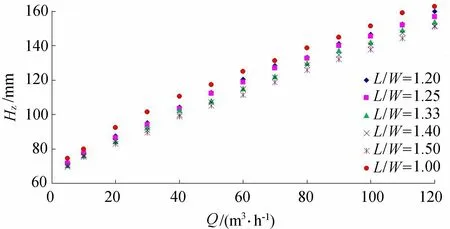
图5 不同展宽比Z形堰流量与堰前水位关系

Z形堰的过流能力还可用流量扩大倍数表示。Z形堰的流量扩大倍数是指相同堰上水头条件下Z形堰过流流量与等宽正交直线堰过流量的比值。计算公式为

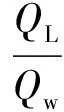
(11)

式中:R为Z形堰流量扩大倍数;QL为Z形堰过流量;Qw为等宽正交直线堰过流量;m0为等宽正交直线堰流量系数。

流量扩大倍数越大,表明堰的过流能力越大,试验中各种Z形堰的流量扩大倍数见表2。由表2可知,各种堰型流量扩大倍数均大于1,说明Z形堰的过流能力大于直线堰。

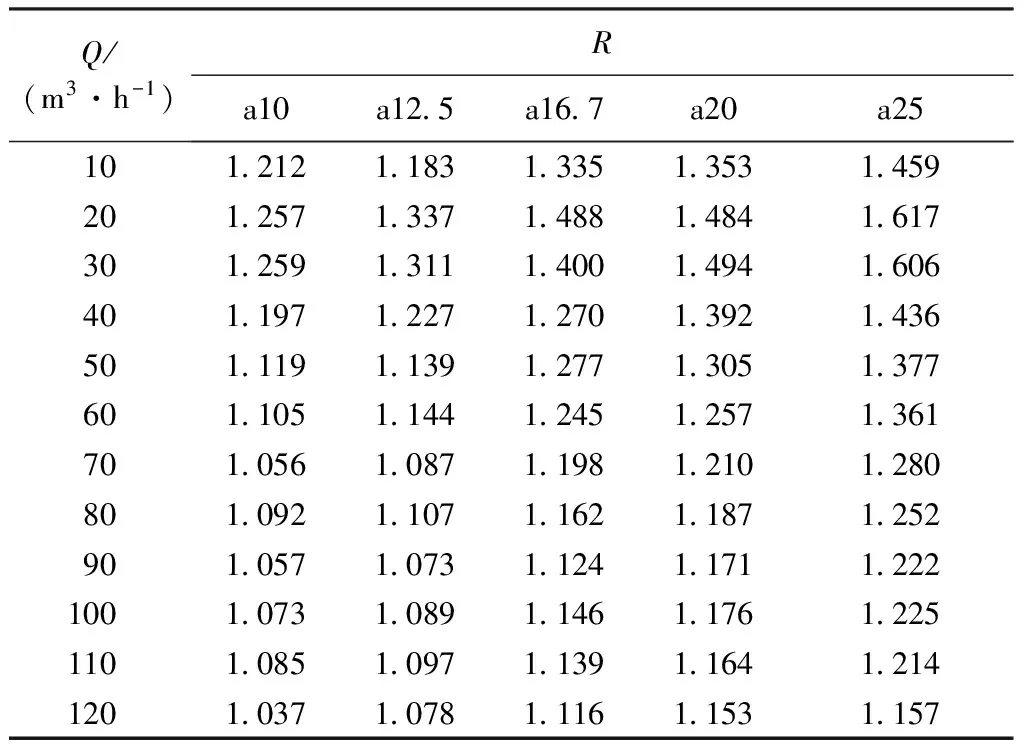
表2 不同试验方案下Z形堰流量扩大倍数

另外,对照表1和表2还可得到,相同流量条件下,L/W越大,流量扩大倍数越大,相同堰型情况下,流量扩大倍数随流量的增大而减小。但从总体看,本试验模型的Z形堰流量扩大倍数不大,主要原因是本试验的Z形堰中间堰与河道平行,即顺河道水流方向,导致过流效率降低。为增大Z形堰的过流能力,可将中间堰改为与河道水流方向呈一定夹角的斜堰。

2.2Z形堰的综合流量系数

2.2.1 试验结果

利用试验流量、堰前断面水位等实测数据,按下式计算Z形堰流量系数值:

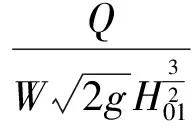
(12)

式中:H01为由前堰堰前断面实测水深、堰前断面实测平均流速按式(5)计算的前堰堰上水头,计算结果见表3。

2.2.2 影响因素分析

a. 流量系数与堰上水深与堰高之比H/P关系。根据试验结果绘制不同Z形堰流量系数mw与H/P的关系如图6所示。图6表明,总体来说H/P越大,mw值越小,展宽比越大这样的趋势越明显;相同H/P情况下,L/W越大,mw越大。

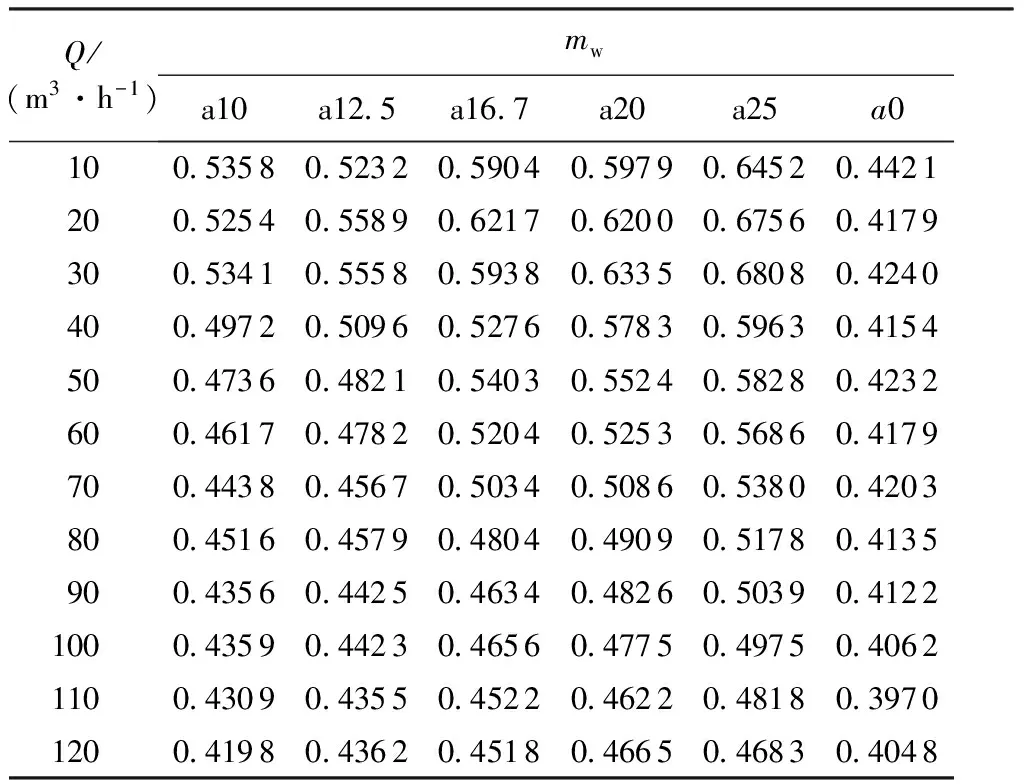
表3 不同Z形堰不同流量的流量系数

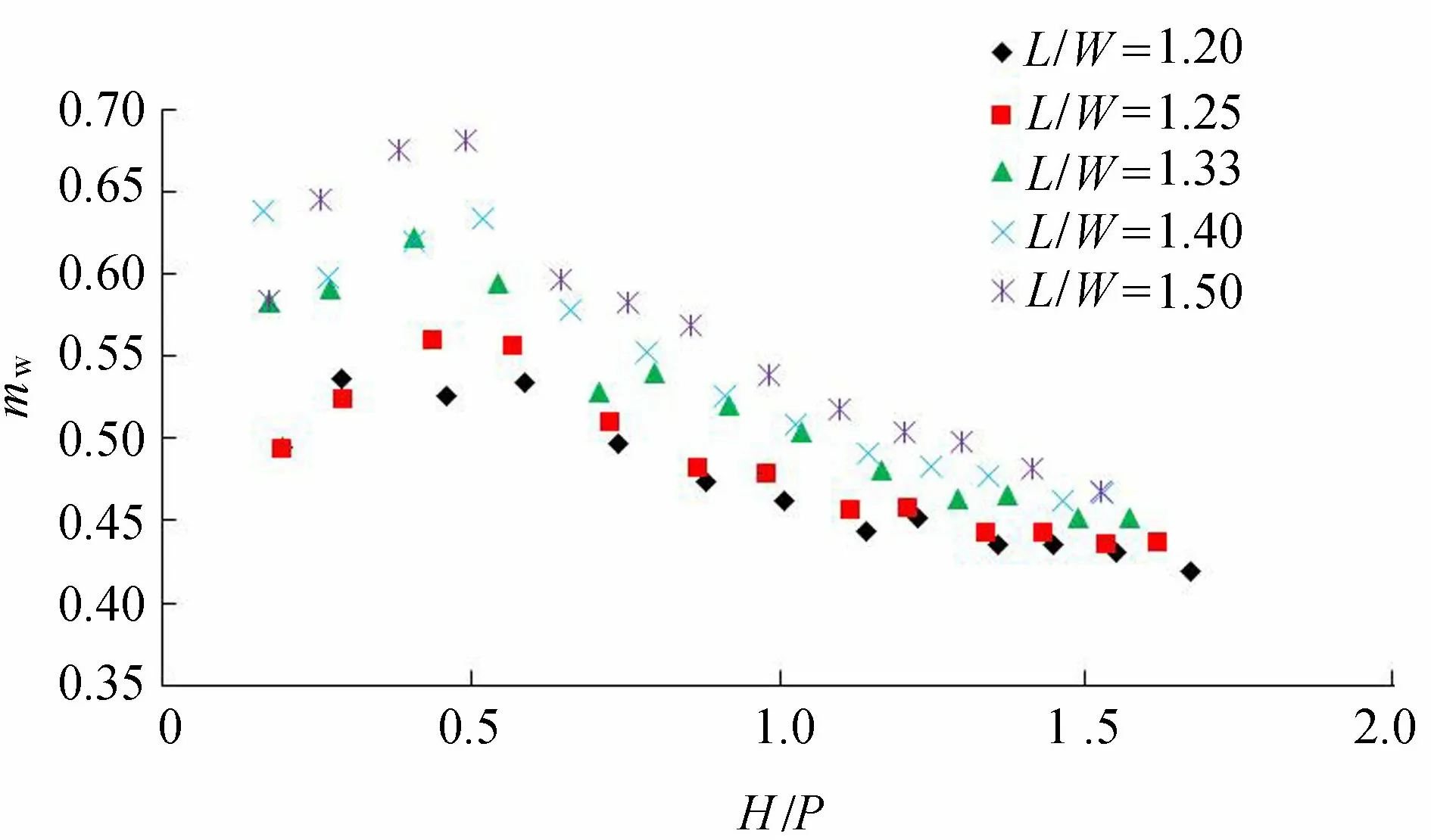
图6 mw与H/P关系

b. 流量系数与a/c关系。根据试验结果绘制Z形堰流量系数mw与前堰宽度与后堰宽度之比a/c的关系(图7)。由图7可知,相同流量下,a/c越大,mw越大,说明在相同河道宽度情况下,增加前堰宽度,Z形堰的过流能力增强。

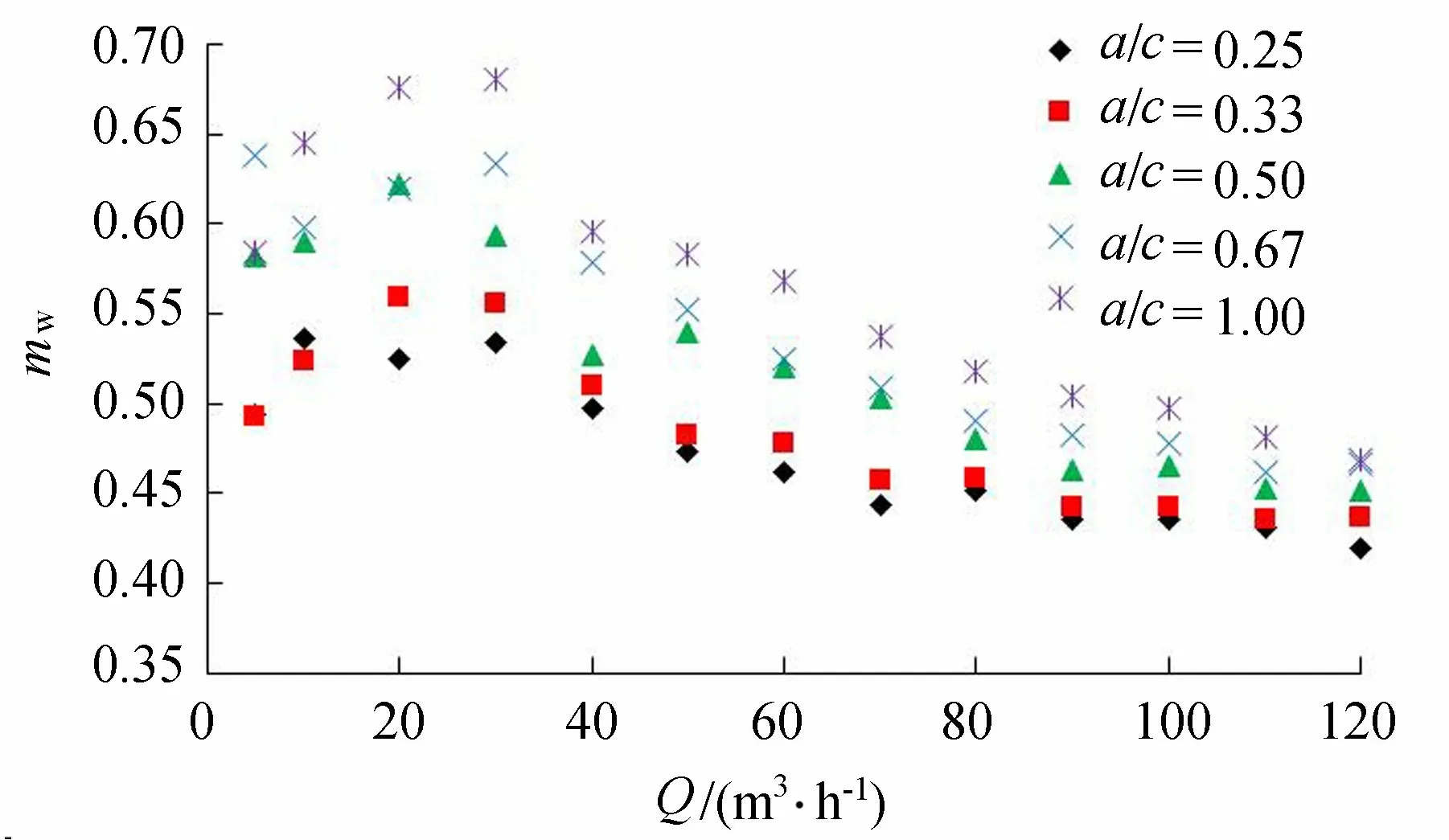
图7 mw与a/c关系

2.3Z形堰流量系数估算公式

由上述分析可知,Z形堰流量系数mw=f(H/P，L/W，a/c),依据表3中前5个方案共60组数据,利用统计分析方法得到Z形堰自由出流条件下流量系数估算经验公式为

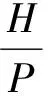
(13)

式(13)的适用条件为中间堰平行于河道、中间堰与前堰长度相等且为自由出流情况。

式(13)的相关系数r=0.951,检验值F=175,均满足要求;显著性检验值sig=0,表明拟合方程(13)存在显著相关关系。另外,对比流量系数实测值(表3)与式(13)计算值可知,式(13)的计算误差在±10%以内,其中误差±5%以内的占86.7%。因此,式(13)具有较高的计算精度,可用于计算Z形堰的流量系数。

3 结 论

利用Z形堰概化水工模型试验数据,对Z形堰的过流能力、综合流量系数等进行计算分析,结果表明:Z形堰的过流能力大于直线堰,展宽比越大,流量扩大倍数越大,过流能力越大;Z形堰的过堰流量可用式(9)计算,该式适用于自由出流情况;Z形堰的综合流量系数与堰上水深与堰高之比H/P、展宽比L/W、前后堰宽比值a/c等因素有关,可用式(13)估算。式(13)适用于中间堰平行于河道、中间堰与前堰长度相等且为自由泄流的情况。

在实际工程中,Z形堰有多种情况。建议对Z形堰淹没出流、前堰与中间堰不相等的情况进行研究,使Z形堰的研究更为丰富。

[1] HAY N, TAYLOR G. Performance and design of labyrinth weirs[J]. Journal of the Hydraulic Division,1970, 96(11): 2337-2357.

[2] DARVAS L A. Performance and design of labyrinth weirs-discussion[J]. Journal of the Hydraulic Division, 1971(8):1246-1256.

[3] 王仕筠,舒以安.迷宫堰水力设计方法的修正[J].江西水利科技,1989(2):36-46. (WANG Shiyun, SHU Yian. Correction of hydraulic design method of labyrinth weir[J]. Hydraulic science and Technology of Jiangxi, 1989 (2):36-46. (in Chinese))

[4] 郭子中.迷宫堰的水力特性及其设计[J]. 砌石坝技术,1984(3):13-21.(GUO Zizhong. Hydraulic characteristics and design method of labyrinth weir[J]. Technology of Masonry Dam,1984(3): 13-21. (in Chinese))

[6] LAUGIER F. Design and construction of the first piano key weir (PKW) spillway at the Goulours Dam[J]. Hydropower and Dams, 2007, 14(5): 94-101.

[7] LEITE R M, PFISTER M, SCHKEISS A J, et al. Hydraulic design of A-type piano key weirs[J]. Journal of Hydraulic Research, 2012, 50(4): 400-408.

[8] EEPICUM S L, FREDERIC L, MCHAEL P, et al. Labyrinth and piano key weirs II[M]. Boca Raton, USA:CRC Press, 2013.

[9] ANDERSON R M. Piano key weir head discharge relationships[D]. Logan: Utah State University, 2011.

[10] 郭新蕾,杨开林,夏庆福,等. 琴键堰泄流能力特性分析[J]. 水利学报, 2014,45(7):867-874.(GUO Xinlei, YANG Kailin, XIA Qingfu, et al. Discharge capacity analysis of piano key weir[J]. Journal of Hydraulic Engineering, 2014, 45(7): 867-874.(in Chinese))

[11] 王仕筠.斜交堰的水力特性[J].江西水利科技,1997,23(1):30-33. (WANG Shiyun. The hydraulic characteristic of skew weirs[J]. Jiangxi Hydraulic Science and Technology, 1997, 23(1):30-33. (in Chinese))

[12] NGUYEN B T. Flow over oblique weirs[D].Delft: Delft University of Technology, 2006.

[13] SAMUEL E T. Discharge coefficient of oblique weirs[D].Logan: Utah State University, 2011.

[14] 黄修筠,拾兵,刘文沛.曲线堰水力学特性的物理模型试验研究[J]. 中国水运月刊,2016,16(6):189-190. (HUANG Xiuyun, SHI Bing, LIU Wenpei. Experimental study on hydraulic characteristic of curved weir[J]. China Water Transport, 2016, 16(6): 189-190.(in Chinese))

[15] 曾甄.迷宫堰水力特性综合研究及其应用[D].南京: 河海大学, 2004.

ExperimentsondischargecoefficientofZ-shapeweirs//

ZHANG Jing1, CHANG Qian2, ZHANG Qinghua1, LI Shuning1

(1.CollegeofWaterConservancyandCivilEngineering,ShandongAgriculturalUniversity,Taian271018,China; 2.YishusiRiverManagementBureau,HuaiheRiverCommissionoftheMinistryofWaterResources,Linyi276000,China)

There is still no research reports on the hydraulic characteristics and discharge capacities of Z-shape weirs. To study the hydraulic characteristics of Z-shape weirs, six schemes of weir shapes and twelve groups of different flow discharges were carried out by model tests, and the experimental data was analyzed. The results show that, the discharge capacity of Z-shape weirsis proved to be stronger than that of linear-type weirs. Furthermore, the ratio of flow discharge of Z-shape weirs to that of linear-shape weirs (in the same channel) increases with the larger ratio of the crest length to the channel width. In addition, the flow discharge of Z-shape weirs can be calculated by the general weir formulas, and the integrated discharge coefficient is related to the water height on the crest (H), the height of weir(P), the crest length, the width of the front and back weir. The discharge coefficient has a positive relation with the ratio of crest length to channel width and the ratio of the front weir width to the back weir width while it had an inverse relation withH/P. A novel experimental formula is established in the consideration ofH/P, the ratio of the crest length to the channel width and the ratio of the front weir width to the back weir width, which can estimate the discharge coefficient of Z-shape weirs.

Z-shape weir; discharge coefficient; ratio of crest length to channel width; discharge capability; experimental study

国家自然科学基金(51409155)

张靖(1988—),女,讲师,博士,主要从事工程水力学与水工结构研究。E-mail: jing16@sdau.edu.cn

张庆华(1960—),男,教授,硕士,主要从事水利工程建设与管理研究。E-mail: zqh@sdau.edu.cn

10.3880/j.issn.1006-7647.2017.06.007

TV132+.29

A

1006-7647(2017)06-0038-06

2017-02-21 编辑：骆超)