一类特殊循环矩阵的若干性质及算法研究

史雨梅,秦 梅

(上海理工大学 理学院,上海 200093)

一类特殊循环矩阵的若干性质及算法研究

史雨梅1,秦 梅2

(上海理工大学 理学院,上海 200093)

基于循环矩阵理论及其相关研究成果,定义了首尾差r-循环矩阵(简记为FLDCMr),研究了它的判别法和对角化问题,给出了求其逆与广义逆的快速算法,并探讨了对其开平方与开m次方的快速算法.

首尾差r-循环矩阵;广义逆矩阵;对角化;开方运算

矩阵是数学中非常重要的一个概念,是重要研究对象,也是进行研究与应用的重要工具[1-2].它可以使所描述的问题通俗易懂且直观明了,刻画问题的本质也更为深刻.矩阵的性质是依赖于其内部元素所具有的特性,由最开始的一种简单的计算方式经由两百多年来无数学者的研究,成为一门数学分支——矩阵论.

循环矩阵是矩阵论中一个重要的组成部分,具有特殊的结构和良好的性质,被广泛应用于数学、物理和现代工程等领域,尤其是在信号处理、分子振动、数理统计、纠错码理论、固体物理、数字图像处理、编码理论、控制理论、矩阵分解、结构计算、平面几何学、三次样条插值、小波变换、计算机时序分析、石油勘测、优化设计、地震物探以及线性预测等领域中应用的特别广泛.近几十年来,循环矩阵理论成为了矩阵论的一个十分热门的研究方向,并且在理论的研究方面取得了快速的发展.

由于特殊循环矩阵具有很多较好的性质和特别的结构,所以应引起我们的关注,并将其进行推广和研究.例如它们的代数性质、行列式、高次幂、秩、非奇异性、特殊结构、对角化、特征值、特征向量、各类多项式表示形式、谱分解、逆矩阵及Moore-Penrose逆的各种算法和相关方程组问题求解及相关算法的计算复杂性分析,等等.

循环矩阵是随着不同领域实际应用中遇到和解决的问题而逐渐发展起来的,其在解决实际问题中起到了中流砥柱的作用,因此吸引了国内外众多的学者进行研究.其中关于特殊循环矩阵的性质、判别法、逆和广义逆以及高次幂等一般表示形式的研究一直都是矩阵分析中重要的课题.那么通过何种方式解决这些问题,得到其性质、判别法、逆和广义逆以及高次幂的一般表达式,完成算法的实现,是近年来人们一直关心的问题并且是研究的热点.

2011年,卢诚波对循环矩阵的平方根问题进行了研究[3].其作者利用依次对矩阵分块降阶的方式给出循环矩阵求逆与循环矩阵相乘的算法,尤其是几类广义循环矩阵求逆与相乘的快速算法,并通过快速傅里叶变换(FFT)来求循环矩阵的逆与矩阵相乘的快速算法,例如用FFT计算鳞状因子循环初等平方根的算法.2013年,何承源教授等人对首尾差循环矩阵的逆和广义逆的快速算法进行了研究[4].2014年,何承源、王晓叶对矩阵

即H-循环矩阵的判别法及对角化进行了研究[5],得出6种H-循环矩阵的判别方法.

2015年,江兆林又对r-循环矩阵的正整数次幂进行研究,并且给出了一般表达式[6].同年,江兆林教授研究了关于Fibonacci数和Lucas数的g-循环矩阵的谱范数,得到‖AF‖2=Fn+1-1,‖AL‖2=Ln+1-1,‖AF2‖2=Fn-1Fn,‖AL2‖2=Ln-1Ln+2等六个等式[7].

对于特殊结构的循环矩阵,许多学者都在不断的进行探索,并且不断的提出新的循环矩阵,如今有近几十种特殊结构的循环矩阵,例如块循环矩阵、对称(向后)循环矩阵、块对称循环矩阵、r-循环矩阵、块r-循环矩阵、二重(r1,r2)循环矩阵、首尾差循环矩阵、首尾和循环矩阵、多重循环矩阵、块因子循环分块矩阵、置换因子循环矩阵、鳞状因子循环矩阵、g-(块)循环矩阵等.

本文在前人研究工作的基础上[8-11]进一步推广,提出一种新的循环矩阵,称之为首尾差r-循环矩阵(简记为FLDCMr).文章有5个章节,首先给出了首尾差r-循环矩阵的一些基本性质,其次研究了FLDCMr的求解逆和广义逆及开平方与开m次方的快速算法[12-15].

1 预备知识

定义1 对于矩阵A∈Cn×n,若有如下结构形式

则称A为n阶首尾差r-循环矩阵,记A=FLDC(a0,a1,a2,…,an-2,an-1)r,简记为A∈FLDCMr.

定义2 称n阶方阵

为基本首尾差r-循环矩阵.

显然,Δ,Δ2,Δ3,…,Δn都是FLDCMr,其特征多项式为g(x)=xn+x-r且

Δ0=In,Δn=rIn-Δ.

由FLDCMr的定义易证下面命题.

命题1 若矩阵A,B∈FLDCMr,则A+B,A-B以及kA(k为任意常数)都是FLDCMr.

定义3[16]设A∈Cn×n,称满足rankAk+1=rankAk的最小非负整数k为A的指标,记为lnd(A)=k.若A非奇异,则lnd(A)=0;若A奇异,则lnd(A)≥1.

定义4[14]设A∈Cn×n,如果存在X∈Cn×n矩阵,使AXA=A,XAX=X同时成立,则称X是A的自反广义逆,记作A{1,2}.

定义5[17]设A∈Cn×n,Ind(A)=k.如果存在矩阵X∈Cn×n满足AkXA=Ak,XAX=X,AX=XA,则称X为A的Drazin逆,记为A{d}.

定义6[18]设矩阵Y∈Cn×n,如果存在矩阵X∈Cn×n,使得X2=Y,则称X是Y的平方根矩阵,此时称Y可开平方,即Y有平方根.

2 首尾差r-循环矩阵的判别法

定理1 矩阵A∈FLDCMr当且仅当A有如下形式

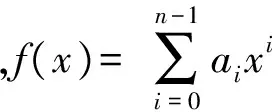
定理2 矩阵A∈FLDCMr当且仅当AΔ=ΔA,其中Δ为基本首尾差r-循环矩阵.

证明 必要性 因为A∈FLDCMr,所以由A和Δ的定义可直接验证得AΔ=ΔA.

充分性 设

由AΔ=ΔA知

所以可得

故A∈FLDCMr.

推论1 若矩阵A,B∈FLDCMr,则AB,BA∈FLDCMr且AB=BA.

证明 因为A,B∈FLDCMr,由定理2可得

AΔ=ΔA,BΔ=ΔB,

因此,ABΔ=AΔB=ΔAB,BAΔ=BΔA=ΔBA,

所以,AB,BA∈FLDCMr.

由定理1显然可得AB=BA.

3 首尾差r-循环矩阵的对角化

首先研究基本首尾差r-循环矩阵Δ的对角化问题.

因为Δ的特征多项式g(x)=xn+x-r有n个不同的根,可设Δ的n个不同的特征值如下:

λ0=ω0,λ1=ω1,…,λn-1=ωn-1.

令V=V(ω0,ω1,…,ωn-1),即

显然V是由ω0,ω1,…,ωn-1构成的非奇异Vandermonde矩阵,且有

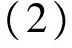
接下来研究一般首尾差r-循环矩阵A的对角化问题.

由定理1和式(2)可得

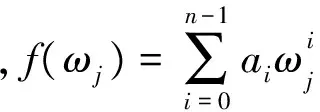
定理3 矩阵A∈FLDCMr当且仅当V-1AV是对角矩阵.

证明 必要性 若A∈FLDCMr,由上面的讨论可知

V-1AV=diag(f(ω0),f(ω1),…,f(ωn-1).

充分性 令V-1AV=P1,P1为对角矩阵,则A=VP1V-1.

令P2=diag(ω0,ω1,…,ωn-1),则Δ=VP2V-1,所以得AΔ=VP1V-1VP2V-1=VP1P2V-1,ΔA=VP2V-1VP1V-1=VP2P1V-1.

而P1和P2都是对角矩阵,所以有AΔ=ΔA,因此,A是首尾差r-循环矩阵.

定理4 矩阵A∈FLDCMr当且仅当其特征值满足条件f(ωi)≠0(i=0,1,2,…,n-1).

证明 必要性 因为A∈FLDCMr,由上面讨论可知

因此,若A∈FLDCMr且A非奇异,则有f(ωi)≠0(i=0,1,2,…,n-1).

4 首尾差r-循环矩阵的逆与广义逆及其数值例子

4.1首尾差r-循环矩阵的逆及广义逆

定理5 矩阵A是非奇异的首尾差r-循环矩阵当且仅当A-1∈FLDCMr.

证明 必要性 由矩阵A是非奇异的首尾差r-循环矩阵及定理2知AΔ=ΔA,则ΔA-1=A-1Δ,所以A-1∈FLDCMr.

充分性显然.

推论2 如果矩阵A是非奇异的首尾差r-循环矩阵,那么矩阵A*∈FLDCMr.

定理6 设矩阵A∈FLDCMr,则A非奇异当且仅当(f(x),g(x))=1.

证明 若A非奇异且A∈FLDCMr,由定理4可知f(ωi)≠0(i=0,1,2,…,n-1),所以f(x)和g(x)没有公共解,即(f(x),g(x))=1.

反之,若 (f(x),g(x))=1,则存在u(x),v(x)使得u(x)f(x)+v(x)g(x)=1,由于g(Δ)=0,f(Δ)=A,则有u(Δ)A=I.

因此,A非奇异且A-1=u(Δ),由定理1可知,A-1∈FLDCMr.

推论3 若矩阵A是非奇异的首尾差r-循环矩阵,则存在A-1=u(Δ).

推论4 如果矩阵A是奇异的首尾差r-循环矩阵,则存在H∈FLDCMr,使得A{1,2}=A{d}=H.

证明 由A奇异可知(f(x),g(x))≠1.

设(f(x),g(x))=d(x),g(x)=d(x)g1(x),f(x)=d(x)f1(x),则(f1(x),g1(x))=1.又g(x)无重根,故(d(x),g1(x))=1,所以(d(x)f(x),g1(x))=1.因此,存在u(x),v(x)使得

式(3)两边同乘f(x),整理得f(x)u(x)d(x)f(x)+f1(x)v(x)g(x)=f(x).由g(Δ)=0,f(Δ)=A得

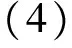
式(3)两边同乘u(x)d(x),同理可得

若H=u(Δ)d(Δ),由定理1可知,H∈FLDCMr,再由式(4),式(5)可知,H=A{1,2}.

又AkHA=Ak-1(AHA)=Ak-1A=Ak,AH=Au(Δ)d(Δ)=u(Δ)d(Δ)f(Δ)=HA,故H=A{d}.

4.2算法与数值例子

由引理1与推论3的证明,可以得到求解首尾差r-循环矩阵逆及广义逆的快速算法.步骤如下:

步骤1 求f(x),g(x)的最大公因式d(x);

例1 已知矩阵A=FLDC(1,-1,1)2∈FLDCM2,求矩阵A的逆矩阵.

解

因为

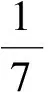
例2 已知矩阵A=FLDC(-2,1,0)10,求矩阵A的逆矩阵.

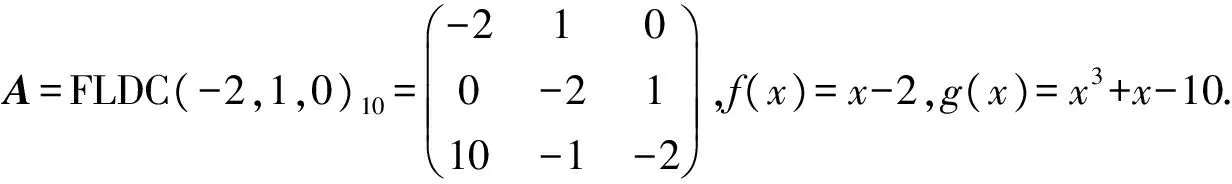
因为(f(x),g(x))=(x-2,x3+x-10)=x-2≠1,所以A奇异.

记(f(x),g(x))=x-2=d(x),则f1(x)=1,g1(x)=x2+2x+5.

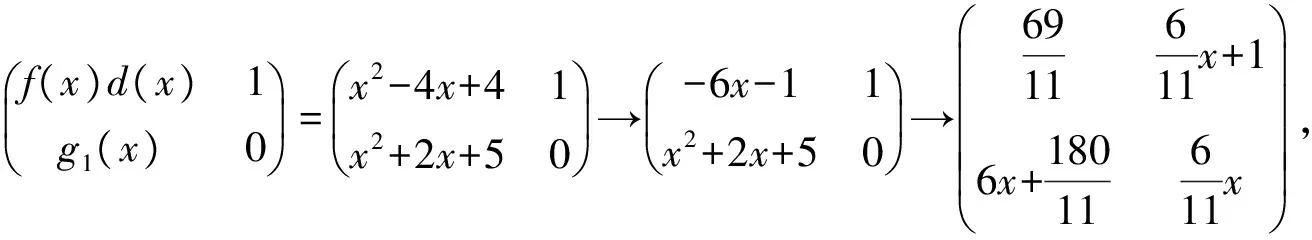
5 首尾差r-循环矩阵开方的快速算法

本章研究首尾差r-循环矩阵在复数域上开方的算法,分析了首尾差r-循环矩阵方根存在的条件与根的求解方法.因为首尾差r-循环矩阵开方所得的结果并非总是首尾差r-循环矩阵,且其个数并非也是有限的,所以这里只讨论方根依旧是首尾差r-循环矩阵的情况.

5.1首尾差r-循环矩阵开平方的快速算法

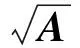
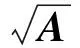
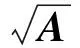
由于ωi(i=0,1,2,…,n-1)是方程xn+x-r=0的n个不同根,所以det(V)≠0,即det(VT)≠0.于是由式(3),可得

即

定理得证.

定理9n阶首尾差r-循环矩阵开平方,所得的根中仍为首尾差r-循环矩阵的有2n个.

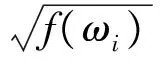
5.2首尾差r-循环矩阵开m次方的快速算法

这里仅研究复数域上首尾差r-循环矩阵的m次方根仍为首尾差r-循环矩阵的情况.

定理10 若矩阵A∈FLDCMr,那么对任意的整数m都存在矩阵B∈FLDCMr是A的m次方根.

证明 若A=FLDC(a0,a1,a2,…,an-2,an-1)r,则有

A=Vdiag(f(ω0),f(ω1),…,f(ωn-1))V-1,

所以得

易知上述矩阵是首尾差r-循环矩阵.

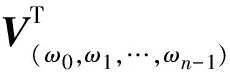
定理11n阶首尾差r-循环矩阵开m次方,所得的根中仍为首尾差r-循环矩阵的有mn个.

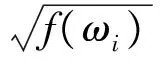
5.3算法与数值例子

(1) 首尾差r-循环矩阵开平方的快速算法及数值算例

快速算法:

① 求出方程xn+x-r=0的n个不同的根ωi(i=0,1,2,…,n-1);

⑤ 得到B=FLDC(b0,b1,b2,…,bn-2,bn-1)r.

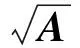
解 由x2+x-2=0解得ω0=-2,ω1=1,

(2) 首尾差r-循环矩阵开m次方的算法步骤

算法步骤:

① 求出方程xn+x-r=0的n个不同的根ωi(i=0,1,2,…,n-1);

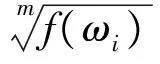
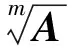
[1] 曾富红,司伟建,曲志昱.基于Hermitian矩阵的特征分解算法[J].沈阳大学学报(自然科学版),2016,28(6):511-516.

ZENG F H,SI W J,QU Z Y.Eigendecomposition algorithm based on Hermitian matrix[J].Journal of Shenyang University(Natural Science),2016,28(6):511-516.

[2] 李艳艳.关于M-矩阵最小特征值界的不等式[J].沈阳大学学报(自然科学版),2017,29(2):164-167.

LI Y Y.Inequality on minimum eigenvalue bounds ofM-matrix[J].Journal of Shenyang University(Natural Science),2017,29(2):164-167.

[3] LU C,GU C.The computation of the square roots of circulant matrices[J].Applied Mathematics and Computation,2011,217(16):6819-6829.

[4] 李静,何承源.求解首尾差循环矩阵逆与广义逆的快速算法[J].山东大学学报(理学版),2013,48(6):96-99.

LI J,HE C Y.A fast algorithm for finding the inverse and generalized inverse of the first and the last difference circulant matrices[J].Journal of Shandong University(Natural Science),2013,48(6):96-99.

[5] HE C Y,WANG X Y.The discriminance for a special class of circulant matrices and their diagonalization[J].Applied Mathematics and Computation,2014,238:7-12.

[6] JIANG Z L,XIN H X.On computing of positive integer powers forr-circulant matrices[J].Applied Mathematics and Computation,2015,265:409-413.

[7] ZHOU J W,JIANG Z L.The spectral norms ofg-circulant matrices with classical Fibonacci and Lucas numbers entries[J].Applied Mathematics and Computation,2014,233:582-587.

[8] SEARLE S R.On inverting circulant matrices[J].Linear Algebra and Its Applications,1979,25(1):77-89.

[9] ROJO O,ROJO H.Some results on symmetric circulant matrices and on symmetric centrosymmetric matrices[J].Linear Algebra and Its Applications,2004,392(1):211-233.

[10] TZOUMAS M G.On sign symmetric circulant matrices[J].Applied Mathematics and Computation,2008,195(2):604-617.

[11] HE C,WANG X.The discriminance for a special class of circulant matrices and their diagonalization[J].Applied Mathematics and Computation,2014,238(7):7-12.

[12] LIU Z,ZHANG Y,RALHA R.Computing the square roots of matrices with central symmetry[J].Applied Mathematics and Computation,2007,186(1):715-726.

[13] LU C,GU C.The computation of the square roots of circulant matrices[J].Applied Mathematics and Computation,2011,217(16):6819-6829.

[14] CARMONA A,ENCINAS A M,GAGO S,et al.The inverses of some circulant matrices[J].Applied Mathematics and Computation,2015,270:785-793.

[15] 潘雪,秦梅.首尾差r-循环矩阵的判别方法及逆和广义逆的快速算法[J].上海理工大学学报,2016,38(3):230-234.

PAN X,QIN M.Discriminance for FLDcircr matrices and the fast algorithm for their inverse and generalized inverse[J].Journal of University of Shanghai for Science and Technology,2016,38(3):230-234.

[16] 曹重光,张显,唐孝敏.高等代数方法选讲[M].北京:科学出版社,2011.

CAO C G,ZHANG X,TANG X M.Selected topics in advanced algebra[M].Beijing:Science Press,2011.

[17] 张凯院,徐仲.数值代数[M].西安:西安科技出版社,2000:28-37.

ZHANG K Y,XU Z.Numerical algebra[M].Xi’an :Xi’an Science and Technology Press,2000:28-37.

[18] 朱德高.一个Jordan块的平方根矩阵[J].数学物理学报,1999,19(3):318-321.

ZHU D G.On square-rooting matrices of a Jordan block[J].Acta Mathematica Scientia,1999,19(3):318-321.

SomePropertiesandAlgorithmsofaSpecialClassofCirculantMatrices

ShiYumei1,QinMei2

(Colloge of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

A new type of circulant matrices,called the first and the last differencer-circulant matrix(FLDCMr),is presented based on the theory of cyclic matrix and its related research results.Its discriminant and diagonalization problem is studied;the fast algorithm of inverse and generalized inverse is given;and the fast algorithm for its square and openm-th power is discussed.

FLDCMr;generalized inverse;diagonalization;root operation

2017-05-15

国家自然科学基金资助项目(11601332);沪江基金资助项目(B14005).

史雨梅(1990-),女,安徽安庆人,上海理工大学硕士研究生.

2095-5456(2017)05-0424-07

O 151.2

A

【责任编辑:肖景魁】