河南辉县南湖水库浆砌石重力坝三维有限元分析
张 龙,杨 鹏,张乐轩
(1.河南省水利勘测有限公司,河南 郑州 450008;2.河南立信工程咨询监理有限公司,河南 郑州 450000)
河南辉县南湖水库浆砌石重力坝三维有限元分析
张 龙1,杨 鹏2,张乐轩1
(1.河南省水利勘测有限公司,河南 郑州 450008;2.河南立信工程咨询监理有限公司,河南 郑州 450000)
构建了以抗拉强度为损伤判断标准的浆砌石本构模型和三维有限元数值模型,分析了河南辉县南湖水库浆砌石重力坝在正常水位、设计洪水位、校核洪水位3种工况下的应力和变形情况,得出在不同工况下该重力坝的应力条件均在规范允许范围之内,但岸坡坝段容易出现拉应力区,需要增加监控措施的结论。
河南辉县;南湖水库;浆砌石重力坝;应力变形;有限元分析;本构模型;数值模型
0 引言
随着计算机技术的发展,大型有限元计算分析软件越来越多地应用于水利工程建设的设计和施工中。大型商业软件如Ansys、Adina、Abaqus等虽然有很多使用上的便利,但是若用于水利工程特定的边界条件或者复杂的结构界面处理,仍有一定的缺陷。
浆砌石重力坝是一种常见的挡水建筑物,主要依靠自身的重量保持坝体稳定。由于其取材方便,施工成本低,适用范围广,在我国中小型工程中得到了广泛应用。由于浆砌石重力坝工程规模小,只要按照相关规范进行设计和建造,就可以满足要求。因此,即使在三维分析软件盛行的今天,对于浆砌石重力坝的分析依然未能深入。常规的重力坝分析体系对浆砌石材料的特点认识不足,因而导致其分析方法不够全面、合理。为此,笔者以河南辉县南湖水库浆砌石重力坝为例,进行了三维有限元数值模拟,分析了不同工况下溢流坝段和非溢流坝段的应力变形分布规律,旨在为工程实践提供一些有益的建议。
1 工程概况
1.1 大坝概况
南湖水库位于河南省辉县市沙窑乡南湖村附近的淇河支流南村河上游,是一座以灌溉、供水为主,兼有一定防洪功能的小(2)型水库。南湖水库大坝为浆砌石+土坝的复合坝型,大坝全长189m,由挡水坝、溢流坝、输水洞组成。主河槽段坝体为浆砌石重力坝,由挡水坝段和溢流坝段组成,挡水坝段分左、右侧两部分,左侧长19m,右侧长33m。浆砌石挡水坝段最大坝高为32.1m,坝长为52m,坝顶高程为560.10m,坝顶宽度为3m,坝顶上游侧设高1.0m、强度等级为C20的混凝土防浪墙,墙厚为0.4m。大坝上游直立, 自高程542.0m 以下坡度为1∶0.15,大坝下游侧自高程556.50m 以下坡度为1∶0.75,坝顶下游侧设置钢栏杆,坝内设排水管。建基面之上,设厚1.5m、强度等级为C20的混凝土垫层。挡水坝和溢流坝段上游防渗面板采用强度等级为C30的钢筋混凝土结构。溢流坝段最大坝高为28.50m,坝长为25m。左岸台地段为均质土坝,坝顶高程为560.80m,最大坝高为3.70m,坝长为112m。下游溢流坝段坝趾处设2m厚、3m宽的混凝土护底,以防止由于水流对坝趾处冲刷而造成破坏。
1.2 坝址区地质岩性
坝址区河道内岩层自上而下分别为表层土、卵石和泥质灰岩。由于高程528.0m至536.0m的卵石层透水率较大,因此拟对高程528.0m以上部分进行开挖清理。两岸坝肩位置岩层自上而下主要为表层土、角砾状灰岩和泥质灰岩。拟对泥质灰岩以上部分进行清除。对清除面的处理,基本上根据泥质灰岩分布情况进行,局部按照安全边坡标准削坡。
2 构建材料本构模型
很多学者都将浆砌石视同混凝土,按均质材料进行数值计算。但是,浆砌石作为砌体材料,具有明显的结构变异性。作为胶结材料的水泥浆在硬化过程中会存在大量微裂缝,砌体之间也会存在少量孔洞,这都会导致砌体结构的不均匀性[1~3]。虽然采用胶结材料的强度值进行计算是保守的算法,但是对于砌体结构产生损伤破坏的机理考虑不够充分。基于砌体结构抗压强度远远大于抗拉强度的特点,本文提出利用抗拉强度作为损伤判断标准的浆砌石本构模型。韦未提出了基于应变空间的混凝土破坏准则,该破坏准则是基于Hesih-Ting-Chen提出的应力空间本构模型的改进形式,如式(1)所示[4]。
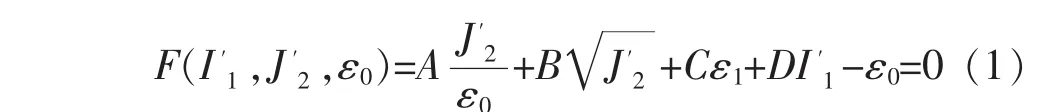
该破坏准则是对Ottosen准则的简化和修正,是Von Mise、Drucker-Prager、Rankine3个破坏准则的线性组合,能够很好地反映浆砌石抗拉破坏的现象。同时,该本构模型也适用于常规混凝土材料。
3 数值计算
3.1 参数选取
根据浆砌石坝体设计规范[5],南湖浆砌石重力坝应按照弹性介质考虑。为了进一步分析坝体的应力分布情况,本文采用了上述的弹塑性本构模型进行模拟,材料参数如表1所示。

表1 南湖浆砌石重力坝材料参数Tab.1 Material parameters of Nanhu reservoir masonry gravity dam
3.2 模型建立
为了消除坝基边界对坝体受力的影响,应尽可能扩大计算范围[6]。南湖浆砌石重力坝有限元分析计算范围为:右岸选取一倍坝高范围;左岸因为与土石坝相接,假定其周围也是山体,选取一倍坝高范围;底部选取1.5倍坝高范围。以顺水流方向为X轴、垂直水流方向为Y轴、竖直方向为Z轴,建立直角坐标系。在坝基周围施加法相约束。将重力坝整体离散为21707个六面体单元、27022个节点,进行有限元分析。坝体整体模型如图1所示。

图1 南湖浆砌石重力坝有限元模型Fig.1 FEM(Finite Element Model)of Nanhu reservoir masonry gravity dam
3.3 计算工况
在对南湖浆砌石重力坝进行分析时,分别对正常蓄水位(556.50m)、设计洪水位(558.78m)和校核洪水位(559.75m)3种工况进行计算。
3.4 计算结果分析
为了计算和分析方便,选取了右岸岸坡坝段(P1)、河床坝段(P2)、溢流坝段边墙(P3)3个典型剖面进行分析。
3.4.1 位移分析
经计算,在校核洪水位下,各剖面的位移等值线分布情况如图2所示,3种工况下各剖面的位移极值如表2所示。
由图2和表2可知,坝体位移与水位高度呈现一定的正相关关系,X方向和Z方向的位移随着水位的升高而增加。溢流坝段的位移增加得更加明显,在正常蓄水位工况下,溢流坝段X方向的最大位移为0.614mm,Z 方向的最大位移为0.715mm;在校核洪水位工况下,溢流坝段在X方向和Z方向的最大位移分别为3.174mm和1.218mm。非溢流坝段的位移变化较小,在正常蓄水位工况下,X方向的最大位移为0.376mm,Z 方向的最大位移为0.60mm;在校核洪水位下,X方向和Z方向的最大位移分别为1.041mm和0.627mm。竖向位移最大值和水平方向位移最大值均出现在坝顶处。总体看来,溢流坝段X方向位移大于非溢流坝段X方向位移,而两者沉降相差不大。

图2 不同坝段剖面位移云图(单位:m)Fig.2 Cloud pictures of different dam section displacement (Unit:m)

表2 不同工况下各典型剖面的位移极值Tab.2 Displacement extremums of each typical section under different working condition
3.4.2 应力分析
浆砌石重力坝主要需要考虑抗拉破坏,而在数值计算中,拉应力主要通过第一主应力反映出来。经计算,在校核洪水位下,各剖面的主应力分布情况如图3所示,3种工况下各剖面的应力极值如表3所示。
从图3和表3可以看出,浆砌石重力坝在正常蓄水位工况下的第一主拉应力最大值出现在溢流坝段,为50.00kPa,而在水位较高的设计洪水位和校核洪水位工况下,非溢流坝段的主拉应力反而变小,分别为19.872kPa 和27.678kPa。 岸坡坝段却呈现出相反的规律,在正常蓄水位工况下,其主拉应力最大值为23.776kPa,在设计洪水位工况下,其主拉应力最大值为69.648kPa,在校核洪水位工况下,其主拉应力最大值为117.85kPa。综合坝体的变形情况可以发现,溢流坝段坝体中部发生沉降较大,而坝踵和坝趾沉降较小,从而导致主拉应力不是在坝踵处出现,而是出现在坝体中部靠近坝踵的地方。在上游水位升高的情况下,坝体整体向下游倾斜,从而导致中部拉应力减小。这说明,在上游有强度较高的防渗结构的情况下,坝体与规范中材料力学法的平截面假定有所不同。而第三主压应力的变化也正好呈现了同样的规律,由于坝体中部沉降的增加,上下游的压应力均有减小的趋势。也正因如此,在校核洪水位工况下,岸坡坝段第一主拉应力达到了117.850kPa,按照损伤本构模型,已经出现了一定的损伤,但仍然在规范允许的范围之内。
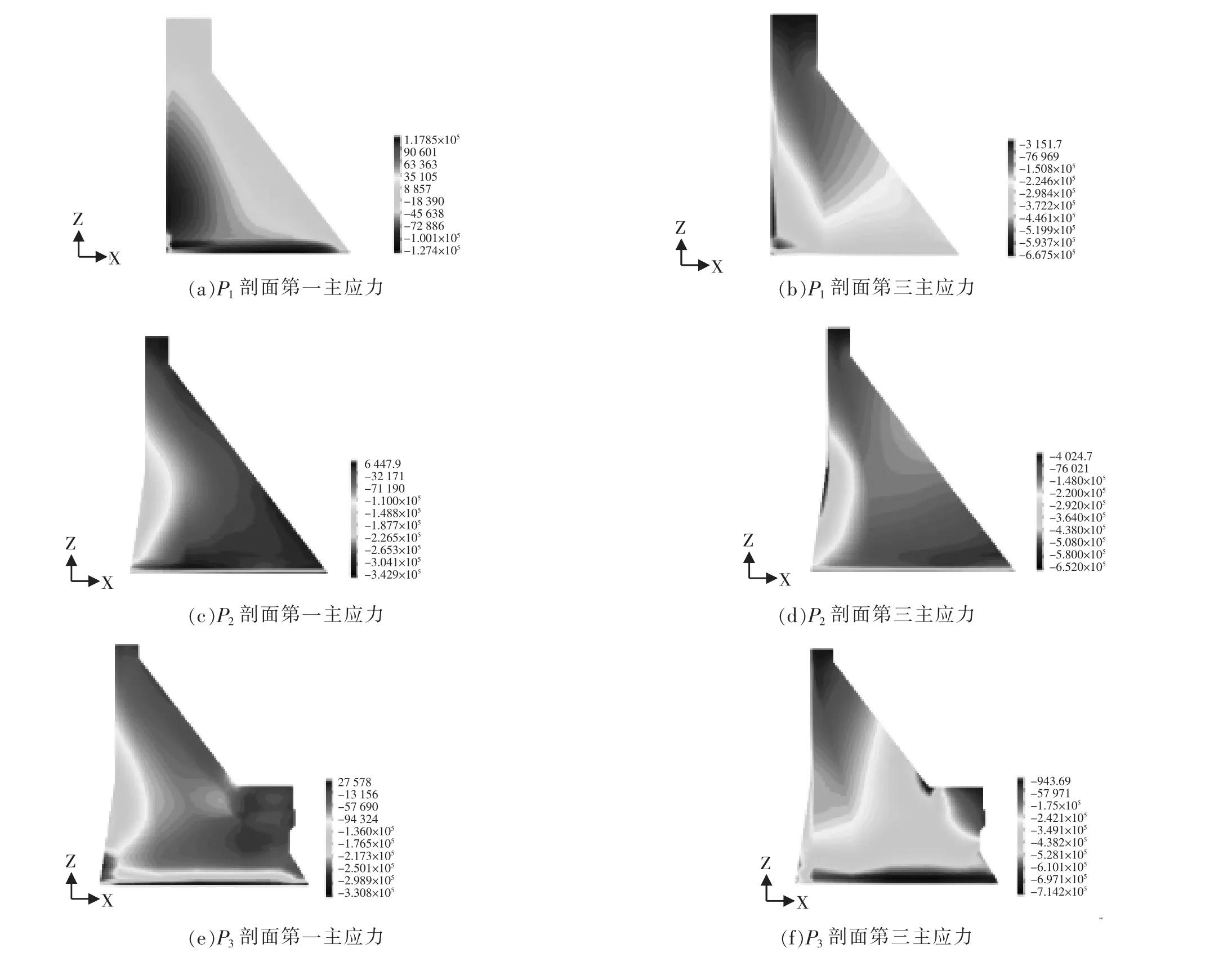
图3 不同坝段主应力分布情况(单位:Pa)Fig.3 Distribution of different dam section main stress (Unit:Pa)

表3 典型剖面在3种工况下的应力极值Tab.3 Stress extremums of typical section under three working condition
4 结语
(1)数值计算的结果表明,利用四参数本构模型分析浆砌石重力坝是适用的,得到的结论也符合一般重力坝的规律。

图3 溢流坝段整体变形云图(单位:m)Fig.3Overflow dam deformation cloud(Unit:m)
(2)在不同的工况下,南湖浆砌石重力坝的应力条件均在规范允许的范围之内。但是,岸坡坝段容易出现拉应力区,需要增加监控措施。
(3)由于浆砌石材料的特性,采用有限元分析法得到的应力分布规律与采用规范规定的材料力学法得到的分布情况有所不同,对这一情况,在以后的设计中应该加以关注。
[1] 许新勇,郭毅,刘宪亮.大型浆砌石重力坝三维有限元结构计算分析[J].黄河水利职业技术学院学报,2006,18(1):1-4.
[2] 朱强,张硕,彭成山.基于ADINA的浆砌石重力坝三维有限元分析[J].水电能源科学,2014,32(7):74-77.
[3] 黄世涛,郭丽朋,朱强,等.某浆砌石重力坝三维有限元分析[J].武汉船舶职业技术学院学报,2016(1):35-37.
[4] 韦未,李同春,姚纬明.建立在应变空间上的混凝土四参数破坏准则[J].水利水电科技进展,2004,24(5):27-29.
[5] 中华人民共和国水利部.砌石坝设计规范:SL25-2006[S].北京:中国水利水电出版社,2006.
[6] 彭成山,王甜,张东东.浆砌石重力坝应力分析研究[J].中国水运,2010,10(5):122-123.
3D FEA(Finite Element Analysis) of Nanhu Reservoir Masonry Gravity Dam of Hui County in Henan
Zhang Long1, Yang Peng2,Zhang Lexuan1
(1.Henan Hydraulic Investigation Co.,Ltd, Zhengzhou450008, Henan, China;2.Henan Lixin Engineering Consultation and Supervision Co.,Ltd, Zhengzhou450008, Henan, China)
According to damage criteria based on strength of extension, it establishes the masonry constitutive model and3D finite element numerical model,analyzes the stress and deformation of Nanhu reservoir masonry gravity dam of Hui country in Henan under three working conditions: ordinary water level,designed flood level and check flood level.It concludes that under different working conditions, this gravity dam stress condition vary in the norm allowed band.The bank slope section needs more monitoring measures because of the easily appearing tensile stress.
Hui County in Henan; Nanhu reservoir; masonry gravity dam; stress deformation;FEA(Finite Element Analysis); structure model; digital model
TV642.3
A
10.13681/j.cnki.cn41-1282/tv.2017.04.002
2017-07-14
张 龙(1988-),男,江苏徐州人,助理工程师,硕士,主要从事水利水电工程设计工作。
[责任编辑 杨明庆]

