信息熵与TOPSIS耦合模型在水利工程防渗设计中的应用

韩晓育 ，刘 迪

（1．黄河水利职业技术学院，河南 开封 475004；2．小流域水利河南省高校工程技术研究中心，河南 开封 475004；3.河南宏景水电工程有限公司，河南 开封 475003）

信息熵与TOPSIS耦合模型在水利工程防渗设计中的应用

韩晓育1，2，刘 迪3

（1．黄河水利职业技术学院，河南 开封 475004；2．小流域水利河南省高校工程技术研究中心，河南 开封 475004；3.河南宏景水电工程有限公司，河南 开封 475003）

建立科学合理的数学评估模型对水利工程防渗设计方案优选具有至关重要的作用。分析了构建信息熵与TOPSIS耦合模型的步骤：建立综合评价体系、确定评价指标权重、确定逼近理想解、确定相对贴近度等，应用该模型对某城市人工湖泊的防渗设计方案进行了综合评价，从而得到最优方案。

信息熵；TOPSIS法；耦合模型；防渗设计；最优方案

0 引言

水利工程防渗设计方案是多指标、多层次的优选过程，其比选信息代表性不强，部分只是统计信息，不能直接作为方案评价信息。当前的防渗设计方案优选多采用单一的优选方法，如基于可拓理论的评价法、灰色聚类分析法、模糊综合评判法等已被应用于设计方案优选中，但这些模型大多带有一定主观性权重赋值，容易导致评价过程信息不全和信息定量准确性不高［1～3］。

笔者试建立信息熵与TOPSIS的耦合模型，对模型中的评价指标进行客观数据挖掘和客观赋予权重，以期解决评价指标权重客观量化准确性不高和不能客观反映数据信息与实际方案之间联系等诸多问题。

1 构建信息熵与TOPSIS耦合模型

建立信息熵与TOPSIS耦合模型需要经历综合评价体系、体系权重赋值、确定方案的逼近理想解、确定方案的相对贴近度等步骤。

1．1 建立方案优选评价体系

此项工作包括两个方面，即对评价样本数据进行无量纲化处理，对方案评价值进行标准化处理。假设m个方案，n 个评价指标，决策矩阵为 X=（xij）m×n。原始数据按照标准化方法进行变换，如式（1）所示。然后，对不同量纲进行归一化处理，完成由实际值到指标评价值的转化。

对于极大型指标，如工程效果、施工工艺、投资等，按照式（2）将实际值转化为指标评价值。对于极小型指标，如施工难度、环境影响等，按照式（3）将实际值转化为指标评价值。

最后，确定归一化决策矩阵的理想解r*j，如式（4）所示。

其中，J+=（极大型指标），J-=（极小型指标）。

1．2 评价指标权重的确定

信息熵对方案中的数据信息量（如投资、施工工艺、工期等因素）和评价指标进行权重赋予［4］，综合考虑TOPSIS法，从各指标信息中获取隐含的指标权重，将各权重值进行综合，得到各评价指标的最终权重。信息熵求解各评价指标权值ωi的表达式如式（5）所示。采用TOPSIS法计算各指标权重ωj的表达式如式（6）所示。耦合模型采用综合权重对各评价指标进行权重赋予，其计算式如式（7）所示。

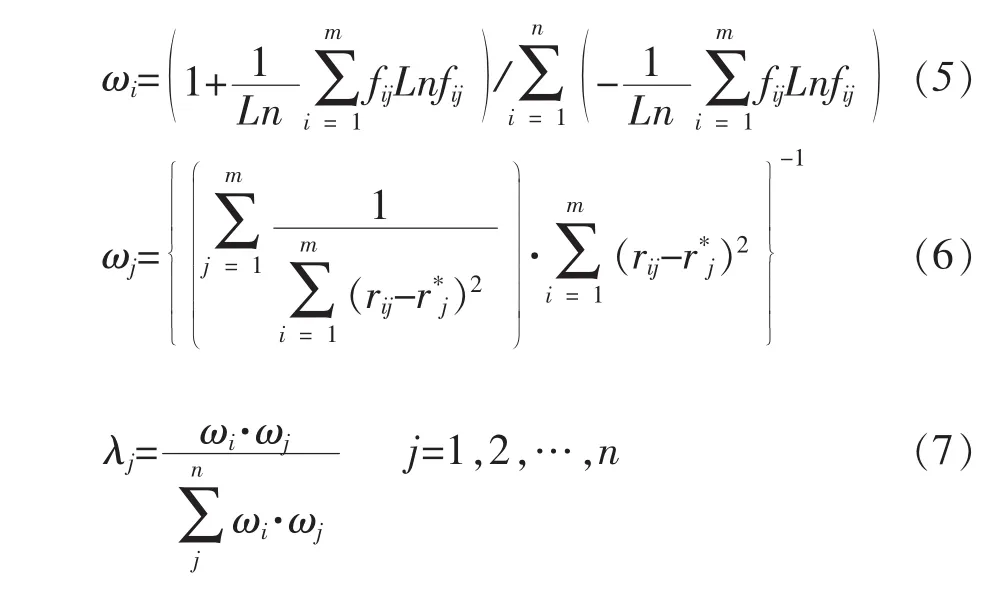
1．3 确定逼近理想解［5］

采用TOPSIS法对各评价方案Mi中相对最优方案的评价指标xij与相对最优方案M0的评价指标x0j之间的关联系数ξij的计算如式（8）所示。

关联度判断矩阵加权，得到关联评价矩阵，如式（9）所示。

逼近理想解V+是属性值，为各候选方案的最佳值，逼近理想解V-则相反，其计算式如式（10）所示。

1．4 确定相对贴近度和最优设计方案

采用信息熵与TOPSIS耦合模型求出各方案的相对贴近度，最终得到最优设计方案［6］。

用式 （11）计算各方案的欧式空间距离，用式（12）计算各方案相对贴近度。

2 案例分析

2．1 工程概况

某城市水系的人工湖泊兼顾防洪排涝、供水排水、景观蓄水和农业灌溉等功能，是水系工程发挥效力的关键所在。以下试采用本文所建立的信息熵与TOPSIS模型，对其渗流设计方案进行评估。

由工程地质勘探资料可知，在钻孔揭露的深度内，湖区地层主要为第四系全新统冲积层和上更新统冲积层根据地层成因类型、岩性及工程地质特性的不同，把勘探地层划分为7层，具体如表1所示。

表1 各层土渗透性指标Tab.1 Permeability index of each layer

经计算和现场监测发现，人工湖区渗漏主要发生在第3层粉沙层和第5层粉细沙层。大量的湖水渗漏会增加湖体运行成本，同时也会抬高周围地区的地下水位，造成部分地区浸没和盐渍化问题，影响生态环境。因此，必须对湖体进行防渗处理，并且防渗体设计要满足湖体运行期防渗的要求，以及防止湖周边地区由于地下水的抬升而引起的浸没盐渍化。同时，还应兼顾湖水与地下水的循环与交换。

2．2 湖体防渗设计方案

湖体防渗设计方案有水泥土搅拌桩（M1）、塑性混凝土防渗墙（M2）和壤土铺盖（M3）3种。水泥土搅拌桩和塑性混凝土防渗墙防渗效果较好，施工期防渗和永久防渗相结合，能够减少排水费用，并且后期运行管理方便。但是，它们对施工工艺要求较高。另外，塑性混凝土防渗墙防渗投资费用高，对环境也有一定影响。壤土铺盖施工工艺简单，可就地取材，对环境影响小，但防渗效果不理想，护体超挖工程量较大，投资费用较高，后期维护也较难。水泥土搅拌桩（M1）、塑性混凝土防渗墙（M2）和壤土铺盖（M3）3种防渗方案的渗漏量分别为209万 m3／a、156万 m3／a、420万 m3／a；主要工程量分别为：总进尺4350m，成墙29295m，超挖土方137．5万 m3、铺盖137．5万m3；总投资分别为574万、1201万、1850万。

2．3 防渗设计方案综合分析

利用信息熵与TOPSIS耦合模型对人工湖泊防渗设计方案进行综合分析，并对设计方案进行优化。选择的7位专家（来自水文、结构、地质、经济等相关领域）按照百分制对备选的防渗设计方案中的评价指标（工效、工期、施工工艺，投资、施工难度、环境影响等）进行了评分［7］，从而对设计方案进行了定量分析，所列评价矩阵如式（13）所示。

用MATLAB R2013B软件对信息熵与TOPSIS耦合模型进行编程，按照耦合模型步骤对上述评价矩阵进行求解，得到防渗方案的权重和相对贴近度［8］。

采用信息熵求得指标的权重ω1=（0.1820.1690.2280.1320.076）。

该防渗的3组设计方案M1，M2，M3对应的各方案的量化指标如表2所示。

表2 3种方案量化指标Tab.2 Quantitative index of three schemes

根据表2可以得出，相对最佳设计方案因素M0＝（0．94130．875740．710．65）。据此列出了方案集M对指标的属性矩阵。

采用TOPSIS法求得各指标的权重ωi=（0.3620.2110.2170.0510.0980.061），采用耦合模型求，得各指标的综合权重λj=（0.3720.1890.2750.0890.0570.014）。

3组设计方案以及对应的各指标组成的多目标决策的关联评价矩阵如式（14）所示。

对关联评价矩阵进行求解，得出相应数值：理想解 V+=[0.3680.1910.2830.0710.0590.016]，负理想解 V-=[0.2670.1340.1850.0310.0300.005]。

利用信息熵与TOPSIS耦合模型，计算出各方案的欧式空间距离：D+=[0.09730.10620.1052]，D-=[0.12310.11890.0703]。各方案的相对贴近度Ci=[0.5610.5020.382]。

根据耦合模型分析结果可知，M1的相对贴近度为0．561，合理性最佳。该耦合模型分析结果与实际相符。在实际评价过程中，往往很难找到有效的历史样本数据，因而对数据的挖掘和客观赋值、对评价方案进行贴近度分析是模型评价的关键。同时，该模型的评价结果受参数影响很小。

3 结语

本文根据水利工程防渗设计方案的不确定性以及评价指标间的关联性等特点，建立了基于信息熵与TOPSIS耦合模型，对设计方案各评价指标进行了量化分析。此外，由于采用客观的信息熵法来确定指标的权重，有效地避免了人为因素的过多干扰。同时，通过TOPSIS法对数据进行挖掘分析和权重赋值、对评价指标进行综合权重赋值，更为客观合理。基于信息熵与TOPSIS耦合模型从客观权重和计算贴近度出发，不需要向神经网络进行样本训练，适用范围广，且模型构建思路清晰，易于实现。

［1］ 郭生练，张俊，郭靖，等．基于气象模式的汉江流域洪水预报系统［J］．水利水电科技进展，2009，29（3）：1－5.

［2］ 王广月，牛之庚，王萌，等．地基处理方案评价的灰色关联逼近理想解法［J］．数学的实践与认识，2011（6）：115－120.

［3］ 李芬，孟刚．模糊综合评判法在围岩稳定性分类中的应用［J］．武汉大学学报：工学版，2011，44（6）：744－747.

［4］ 丁琨，金菊良，张礼兵，等．基于信息熵的污水处理厂规划改造决策评价投影寻踪模型［J］．给水排水，2010，36（5）：166－170．

［5］ 陈红艳．改进理想解法及其在工程评标中的应用［J］．系统工程理论方法应用，2004（10）：471－475.

［6］ 周会军，肖英杰，张浩．基于改进灰色关联分析法的码头设计方案优选［J］．上海海事大学学报，2011，32（3）：11－15.

［7］ 霍映宝，韩之俊．基于广义最大熵原理和遗传算法的多指标权重确定方法研究［J］．数理统计与管理，2005，24（3）：39-44.

［8］ 金菊良，吴永林，汪明武．城市防洪标准方案优选的组合权重方法［J］．四川大学学报：工程科学版，2004，36（4）：l－5.

TV543

B

10．13681／j．cnki．cn41－1282／tv．2017．04．005

2017-04-17

河南省科技攻关项目：基于统计模式识别技术的水工结构损伤诊断（142102310122、132102310320）；黄河水利职业技术学院青年科研基金项目：基于模糊层次分析法的水利工程投资风险管理研究（2016QNKY002）。

韩晓育（1984-），女，河南洛阳人，助教，硕士，主要从事水利工程造价及风险管理的教学与研究工作。

[责任编辑 杨明庆]