某型教练机下半框拓扑及尺寸优化

张勇，周恒，陈里根，袁平湘，陈龙辉

（航空工业洪都，江西南昌330024）

某型教练机下半框拓扑及尺寸优化

张勇，周恒，陈里根，袁平湘，陈龙辉

（航空工业洪都，江西南昌330024）

某型教练机因吊舱结构更改，需要对下半框进行重新设计，以利于载荷的传递。本文根据其受力形式，在一定强度和刚度约束条件下、在Optistruct中对其进行拓扑和尺寸优化。结构优化后与初始结构的有限元分析对比发现，其结构的应力水平下降、刚度提高，并减少了下半框的重量。

框；Optistruct；拓扑；尺寸优化

0 引言

飞机结构设计是一个反复迭代设计的过程，在满足飞机所需性能的前提下，减少重量是飞机设计师永恒的追求，航空领域中也有“为减少每一克重量而奋斗”的说法。在仿真技术成熟的今天，CAE技术的飞速发展，为产品生产前进行性能评估，提高产品品质、低成本设计提供了一个非常有效的工具。CAE不仅能起到性能分析的作用，还可通过先进的优化设计方法，实现结构的优化设计及减重。

本文针对某型教练机机身下半框结构采用两级优化，在一定强度和刚度条件下在Optistruct中进行一级拓扑优化和二级尺寸优化，极小化其重量。

1 下半框概述

因吊舱结构更改，采用倒装可投放形式安装在机身腹部，并在吊舱前段增加整流罩。因吊舱整流罩处的Y向载荷较大，将下半框补全，为吊舱整流罩提供支撑。

如图1所示，在机身腹部某框处增加一个框板，框板两端通过铆钉和抽钉与下大梁连接，同时框板通过螺钉和托板螺母与腹部口盖相连。为将吊舱的Y向载荷通过框板向上传递，在框板上端布置两个角盒，角盒下端通过螺栓和铆钉与框板连接，角盒上端通过螺栓与设备舱地板连接，将载荷向上传递，如图2所示。

下半框、角盒选用的材料为7050铝合金，其材料参数：抗拉强度σb=510MPa，弹性模量E=71000MPa，泊松比μ=0.33，密度ρ=2.8g/mm3。

2 拓扑及尺寸优化

2.1 拓扑优化

拓扑优化寻求结构的某种布局，使其能够在满足一定约束条件的情形下，让某种性能指标达到最优。即在一个确定的连续区域内寻求结构内部非实体区域位置和数量的最佳配置，寻求结构中的构件布局(如结构内有无孔洞，孔洞的位置、数量以及组合结构中构件的连接方式等等)及节点联结方式最优化，使结构能在满足应力、位移等约束条件下，将外载荷传递到结构支撑位置，同时使结构的某种性能指标达到最优，其示意如图3所示。

拓扑优化设计变量是单元的相对密度，相对密度是指伪密度，表征材料的有无，以区间[0,1]表示，0表示无，1表示有，区间内表示中间密度，图4中红色区域显示为高密度单元，绿色区域表示的是中间密度单元，这些区域显示了材料的最佳分布，即传力路径。

拓扑优化的数学模型：

式中：X是单元密度；f(x)是目标函数；g(x)是不等式约束函数；h(x)是等式约束函数。

2.2 尺寸优化

在保持结构的形状和拓扑结构不变的情况下，寻求结构组件的最佳截面尺寸以及最佳材料性能的组合关系，优化截面的最优面积（如图4桁架），选择板的最佳厚度等称为尺寸优化，其特点是：设计变量容易表达，求解理论和方法成熟[2]。

尺寸优化是一种细节优化设计方法，是设计人员在概念设计的基础上所进行的设计。它是通过改变结构单元的属性——例如壳单元厚度、梁单元的横截面属性、弹簧单元的刚度和质量单元的质量等以达到一定的设计要求（如应力、质量、位移等）。

3 下半框结构优化

3.1 载荷与约束处理

下半框为吊舱整流罩提供支撑，通过吊舱整流罩上的顶杆相互作用，并受到顶杆Y向正向3.5t的载荷，其大小：

由于顶杆与下半框框缘通过面与面之间接触，接触面如图5阴影所示，故将上述载荷转化为面压力，

接触面面积：

(3)课堂教学活动的开展：教师在课堂上可以先运用优慕课App的“在线测试”发布预先设置好的测试题对学生进行简单测试，了解课前自主学习情况，然后根据测试结果有针对性地对重点、难点知识进行详细讲解。讲解完成后，让学生分组进行实时练习和互教互学。最后，教师给学生简单说明下一次的课前自主学习任务。

对下半框进行结构力学分析，根据圣维南原理，外界约束对约束局部区域应力影响显著，对远处区域应力影响无显著差异。为避免局部约束对下半框应力的影响，在结构分析时将左右下大梁、角盒和下半框一起进行力学分析，约束左右下大梁两端和角盒顶部X、Y、Z三个方向的平动自由度。

3.2 初始结构有限元分析

对初始结构进行有限元建模，采用四面体网格对其进行网格划分，赋予网格壳单元属性，在顶杆与框缘接触面处施加压力载荷，并约束角盒顶部、左右下大梁两端X、Y、Z三个方向自由度后，将有限元模型（如图6所示）提交结构分析软件计算，其变形和应力结果如图7、图8所示。

对初始结构进行有限元分析，下半框最大应力为491MPa，最大变形1.85mm，初始结构总应变能16061J，应力水平小于材料7050的抗拉强度510Mpa，强度基本满足要求，但重量为1.283kg，重量太重，故在满足结构的强度和刚度条件下，对下半框进行结构优化，极小化其重量。

3.3 下半框拓扑优化

在满足结构的强度和刚度条件下，对下半框进行结构优化，首先对其进行拓扑优化。在给定的密度下，在一定强度和刚度条件下，极小化下半框的体积。结构的静刚度一般可以用在特定载荷下的柔度来度量，柔度越小，结构的静刚度越大[3]。柔度作为结构总刚度逆的度量，用结构的总应变能进行表征，定义为：

为保证下半框在满足强度要求的同时，能够提供一定的支撑刚度，建立如下下半框拓扑优化数学模型：

式中：V是结构体积，σ是结构的应力，C是结构的总应变能，K是结构的总体刚度矩阵，U是结构的位移，F是外载，X是设计变量，即拓扑优化的相对密度。

由于拓扑优化对应结构设计的概念阶段，是在给定的设计空间寻求材料的最佳分布，或者传力路径，从而在满足各种性能的条件下得到重量最轻的设计，故将下半框进行初始重新设计作为拓扑优化设计域，角盒、下大梁作为非设计域，并进行有限元建模，其模型如图9所示。

将建好的有限元模型提交Optistruct运算，经过35次迭代运算，得到拓扑优化材料单元密度云图、目标函数、总应变能迭代如图10～图12所示。

经过拓扑优化，得到下半框的材料分布形式，最佳传力路径。优化的目标函数、总应变能趋于稳定并收敛，下半框体积为10874mm3，结构总应变能为9792J。将拓扑优化结果导入CATIA对下半框进行三维重构，得到下半框结构如图13所示。

3.4 下半框尺寸优化

将下半框重构模型的上框缘、下框缘、腹板厚度、两筋条及筋条连接区域厚度作为设计变量进行尺寸优化，其尺寸定义如图14所示，设计变量初始值：X1=2、X2=3、X3=4、X4=6、X5=9、X6=1.5。

和拓扑优化外界约束和目标函数一样，在已知材料密度下，在一定强度和刚度条件下，最小化下半框体积，尺寸优化数学模型：

将重构后的下半框与角盒、下大梁建立有限元模型，其模型如图15所示。

将建好的有限元模型提交Optistruct运算，经过8次迭代运算，目标函数和结构总应变能趋于稳定并收敛，尺寸优化的目标函数、总应变能、设计变量迭代图如图16～图23所示。

经过尺寸优化，得到下半框框缘、腹板、筋条设计变量尺寸见表1。

根据尺寸优化后的设计变量，以此作为参考并考虑制造加工工艺，重新定义设计变量值，取X1=1、X2=4.5、X3=2、X4=5.5、X5=6、X6=1，将改变厚度后的框缘、加筋条、腹板的下半框与角盒、下大梁重新建立有限元模型并提交运算，得到尺寸优化后的结构变形与应力结果如图24～图25所示。

对尺寸优化后的结构进行有限元分析，下半框最大应力为472.8MPa，最大变形1.55mm，结构总应变能9584J，应力水平小于材料7050的抗拉强度510MPa，满足结构的强度要求，对比图7、图8，优化后的结构受力变形更均匀，尺寸优化后的模型如图26所示。

初始结构和优化后的结构数模、最大变形、应力、总应变能、重量对比如表2所示。

由表2可知，优化后下半框的应力下降了3.7%；变形下降了16.2%，总应变能下降了40.3%，相应的结构刚度得到提高；重量下降了67.6%，达到了在一定结构强度和刚度条件下，减小下半框重量的目标。

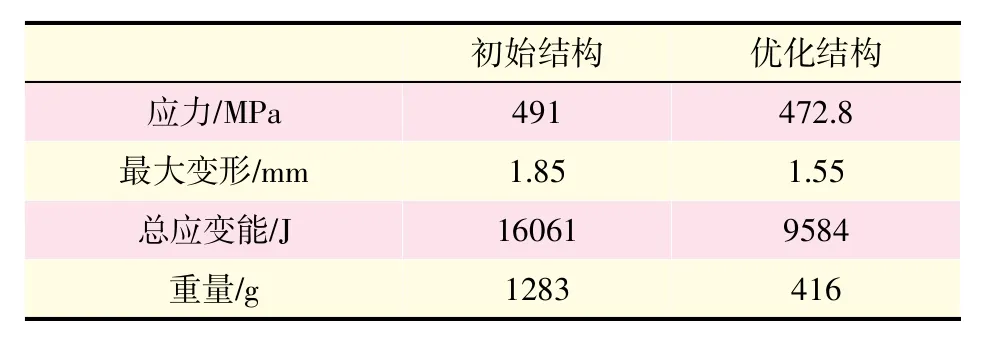
表2 初始结构和优化结构对比

4 结语

在满足一定强度和刚度约束条件下，采用拓扑优化方法对下半框进行优化设计，获得框的最佳材料分布形式；基于拓扑优化后的三维重构模型，对其进行尺寸优化，得到框缘、腹板、筋条设计尺寸。以此为参考并考虑制造加工工艺对结构进行改进设计，完成尺寸优化后的建模，得到详细设计阶段数模；对比初始结构和优化结构有限元分析结果，优化后结构受力更加均匀，应力水平下降，刚度提高，下半框结构的重量减少，达到了结构优化的目的，实现了下半框的重新设计。

[1]汤颖颖.基于变密度法的连续体拓扑优化设计[D].西安：长安大学,2008,1.

[2]左孔天.连续体结构拓扑优化理论和应用研究[D].武汉：华中科技大学,2004,9.

[3]李东泽，于登云，马兴瑞.航天器桁架结构拓扑优化设计[J].中国空间科学技术,2009,(4):1-7.

Topology and Size Optimization of Lower Half Frame of One certain Type of Aircraft

Zhang Yong,Zhou Heng,Chen Ligen,Yuan Pingxiang，Chen Longhui
(A灾IC-HONGDU,Nanchang,Jiangxi 330024)

Due to change on pod structure,one certain type of aircraft is required to re-design lower half frame to facilitate transfer of load.Based on its load bearing form and under certain restriction conditions for strength and rigidity,this paper makes topology and size optimization in optistruct.Finite element of the optimized structure and finite element of the original structure are analyzed and compared,which shows the optimized structure has reduced stress,improved rigidity,and reduced the weight of lower half frame.

Frame；Optistruct；Topology；Size optimization

2017-08-15）

>>>作者简介 张勇，男，1988年6月出生，2014年毕业于西北工业大学，工程师，主要从事飞机结构设计工作。