基于时间序列分析的人体摔倒过程预测

中国船舶重工集团公司第七一三研究所 潘文涛

基于时间序列分析的人体摔倒过程预测

中国船舶重工集团公司第七一三研究所 潘文涛

可穿戴式下肢助行机器人的稳定恢复性能对平衡能力较弱的穿戴者安全性至关重要。针对大干扰下的稳定恢复控制应用，对人体摔倒过程中的动力学及足底压力变化特征进行分析，通过计算足底压力中心点（CoP）与足底有效支撑区域多边形边界的距离，从而可以实现对人体的稳定性的定量描述。通过自回归(AR)时间序列模型、最小二乘法(LS)、AIC准则函数等相关理论，建立摔倒过程稳定裕度的时间序列预测模型，实现对人体摔倒过程的预测识别，为摔倒过程的稳定恢复控制策略研究提供依据。

助力机器人；摔倒过程；零力矩点；时间序列

引言

随着人口老龄化问题的加深，可穿戴式助力机器人在助老行走中具有很大的应用前景[1]。下肢助行机器人行走时，理想情况下可通过控制机器人快速跟随穿戴者运动，为穿戴者提供助力。然而，在穿戴者有摔倒的趋势时，助力机器人采取快速跟随的控制策略，会加速穿戴者的摔倒过程，加重对穿戴者造成的伤害。提前预测穿戴者的摔倒趋势，并采取相应的控制策略，协助穿戴者重新处于稳定状态，可避免摔倒对人机系统造成损伤，在摔倒趋势无法逆转时，可控制机器人采取相对安全的摔倒姿势，从而给予穿戴者一定的保护。本文针对大干扰下助行机器人的稳定恢复控制的需求，深入研究人体摔倒预测算法。

在外骨骼下肢助行机器人系统中，稳定性控制方法大部分都是基于ZMP理论，根据穿戴者或者机器人的关节角度、角速度以及加速度信息，计算实际的ZMP位置，再基于ZMP理论实现稳定控制[2]。这些方法存在一定的局限性，首先，基于ZMP稳定性控制方法，机器人的足底必须水平着地，这与人在行走过程中的特点相违背。其次，根据实际运动数据计算ZMP位置，是基于动力学模型，需要精确的参数，对于不同体型的穿戴者来说适应性受限。再有，这些方法是对当前时刻的稳定性进行分析，实时性很难保证，很难满足安全性需求。在穿戴者处于摔倒趋势时，如果提前能够预测识别出摔倒趋势，根据识别结果采取相应的控制策略，能够弥补目前稳定性控制方法的不足。

目前，许多学者采用加速度传感器、角速度传感器监测人体运动过程，选取合适的传感器测量阈值对人体摔倒进行判定，应用于对摔倒后的人体进行监测、定位及报警[3-5]。近年来更多的研究集中于对摔倒行为的预测，防止摔倒的发生。对摔倒进行预测，延长摔倒的筹备时间，是摔倒识别相关方向的发展趋势。针对辅助下肢健全老人行走应用，现有摔倒识别方法没有结合考虑摔倒过程的动力学稳定性变化情况，而人体的摔倒行为实际上是一系列变化的过程，在这个变化的过程中，人机系统的稳定性也随之变化，为了实现该过程的稳定恢复，需要根据摔倒过程中不同稳定程度采取不同的策略。因此，在摔倒预测研究中，除了在识别算法上基于历史数据建立预测模型外，应该对摔倒过程的稳定性进行分析，采用能直接反应动力学稳定性的方法，对摔倒过程各阶段稳定性进行定量的描述，为可穿戴式助力机器人的稳定恢复控制策略研究提供依据。

1 稳定性定量描述

基于摔倒过程稳定恢复控制应用，在对摔倒进行预测时，需要对稳定状况作定量的研究和分析。零力矩点（ZMP, Zero Moment Point）理论是目前类人机器人常用的稳定性分析方法。ZMP是指地面反力向水平面中某点的等效，合力矩为零的点。一般将ZMP与双足形成稳定支撑区域多边形边界的最短距离定义为稳定裕度，稳定裕度是描述人体运动过程稳定性最直观有效的指标。

ZMP在一定程度上可以由足底压力中心点(CoP)等效代替[6]。由于足底压力检测相对简单方便，且足底压力中心点计算简便，因此本文采用CoP代替ZMP的方式计算摔倒过程中的稳定裕度。

1.1 足底压力中心点

人体在运动过程中，CoP的位置处于不断变化的状态，平稳状态下处于小范围内移动；摔倒过程中CoP会沿着摔倒方向发生快速移动。

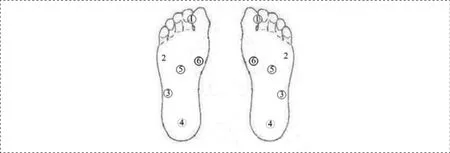
图1 足底压测量点

本文根据安装在足底的压力传感器信号，实时计算CoP与支撑各个边界的最短距离d，从而完成对人体运动中的稳定性状况进行定量描述。足底压力测量点位置如图1中所示。

由式（1）计算出压力中心点的坐标[XCoP,YCoP,]，其中Fi为压力传感器测量值，[xi,yi]为其对应的坐标值。

1.2 双足支撑多边形

如图2所示，人体在正常站立时，由图2所示的左右脚中的传感器1、2、3、4构成最大的支撑区域。在稳定裕度的计算中，依据足底压力的信息计算对应时刻的支撑区域多边形。

图2中外围多边形即为双足正常站立时的支撑区域，内部曲线为人体向前摔倒过程中CoP的变化轨迹，从图2中可以看出在前向摔倒过程中CoP沿摔倒方向与支撑区域边界的距离逐渐减小。

图2 摔倒过程CoP变化曲线

在计算稳定区域时，根据足底压力信息，除去足底压力为零的传感器，选择最外部的足底压力传感器，并确定其坐标[xi,yi]。将[xi,yi]作为支撑多边形的顶点，支撑区域多边形的边界采用直线方式进行拟合，由式（2）可以确定支撑区域的各个边界。

[x1,y1]，[x2,y2]为两相邻的足底压力传感器的坐标。定义变量：

从而可以得出CoP到各个边界的距离值：

2 摔倒预测算法

摔倒过程中，可以将稳定裕度看作是与时间相关的序列，可以建立合适的时间序列预测模型，通过预测模型对人体的稳定裕度进行多步预测，从而提高系统的响应速度，得到未来时刻人体稳定裕度的状况，作为助力机器人稳定恢复控制策略的依据。

相邻时刻的稳定裕度值存在一定的相关性，如图3中所示，通过过去时刻的稳定裕度值，可以预测未来时刻稳定裕度值。选择合适的时间序列预测模型，可以实现对摔倒过程的稳定裕度曲线进行快速准确的预测，从而预测出人体的稳定状态。

图3 预测原理示意

2.1 时间序列模型

采用时间序列进行预测时，选取不同的时间序列模型对预测结果的准确性和实时性有非常大的影响。常用的时间序列模型有：自回归(AR)、移动平均(MA)、自回归移动平均(ARMA)[7-8]。通过试验获取人体摔倒过程足底压力传感器数据，从而可以计算人体摔倒过程中稳定裕度的时间序列，计算该序列的自相关、偏相关系数，依据经验和现有理论可以选择最优的时间序列模型。各中时间序列模型所对应的自相关、偏相关系数特征如表1中所示：

表1 时间序列模型阶次

图4、图5分别为根据某次摔倒试验所计算的稳定裕度时间序列的自相关以及偏相关系数。

图4 稳定裕度曲线的自相关系数

图5 稳定裕度曲线的偏相关系数

从上图中可以看出人体在摔倒过程中稳定裕度的时间序列的自相关系数呈拖尾性，偏相关系数呈现截尾性，符合典型的AR时间序列模型特征，因此本文选择AR模型作为人体摔倒过程的预测模型。

AR(p)时间序列模型满足式（5）～式（7）的条件：

对于AR（p）时间序列模型来说，Xt仅与Xt-1，Xt-2，…，Xt-p有线性关系，在Xt，Xt-1，Xt-2，…，Xt-p已经确定的情况下，Xt与其它时刻观测值无关，εt是一个均值为零的白噪声，仅对Xt有影响。

2.2 模型定阶

AIC准则即最佳准则函数法是目前最常用的时间序列模型定阶方法。AIC准则是采用准则函数对预测模型和原始数据的拟合程度，以及模型中待定参数的个数进行描述。AIC准则函数的一般形式为：N为样本个数，为时间序列残差，P时间序列待定参数个数。

由图4、图5可知，AR(p)时间序列模型阶次不大于10。采用人体摔倒过程的稳定裕度训练数据计算AR时间序列模型各阶次的AIC函数值。实际计算可知，AR模型的AIC函数在6阶之后AIC函数不再减小，因此，采用AR(6)模型对稳定裕度时间序列进行预测。

2.3 模型参数辨识

确定时间序列模型参数是时间序列分析的一个最重要的环节，模型参数的选择直接影响到预测误差的大小和预测速度。最小二乘法是系统辨识理论中参数估计的最经典方法。最小二乘法进行参数估具有先验知识少、计算量小、收敛性能好，算法简单等优点。

对于AR（p）模型未来时刻的值y(t)可以由以下公式计算获得，y(t — p)为p时刻前的观测值，ε(t)为均值为零的白噪声[14]。

定义向量：

则AR(p)模型的残差可以表示为：

最小二乘法参数估计的原理就是寻求θ的估计值，使其极小化残差的平方和：

定义向量：

残差的平方和可以表示为：

由上式可以确定θ的估计值：

使得残差的平方和J最小，θ的估计值即为最优的AR(P)时间序列模型的参数。

2.4 预测流程

时间序列预测算法流程如图6中所示。首先选定训练数据，采用最小二乘法和AIC判别准则取定最优的时间序列模型阶次和参数，再由得到的预测模型测试数据进行预测。

图6 预测程序流程图

3 试验与结果分析

足底压力信号采集采用贴片式压力传感器，安装在鞋垫底部，具有轻便、精确、不影响人体运动状态的特点。

人体摔倒过程时间短暂，对人体摔倒过程的分析需要有较高的数据采样频率。DSP芯片相对于单片机具有功耗低、运算速度快、运算精度高的优点。足底压力采集系统由DSP芯片STMS320C2812及附属电路组成的最小系统构成，实现对双脚12个足底压力传感器的实时数据采集。

本文让试验者穿着鞋垫底部装有多个压力传感器的鞋进行多次摔倒试验。试验者身高165cm，体重55kg，选取了四个典型的摔倒过程：前向摔倒、后向摔倒、左摔和右摔，每组摔倒过程分别采集60组数据，选取40组摔倒过程信息作为训练数据，其它作为测试数据，每个完整的摔倒过程足底压力信息采样点约为2000个。

本文以前摔过程作为示例，整个摔倒过程足底压力变化曲线如图7所示，结合前文所述的稳定性判别方法，可以计算出摔倒过程中的稳定裕度变化曲线，将其视为与摔倒时间相关的一个时间序列。

图7 摔倒过程足底压力曲线

由最小二乘法计算得到AR(6)时间序列模型的参数如表2中所示：

表2 AR时间序列预测模型参数

由于摔倒过程时间比较短，为了提高频率响应，对摔倒过程的稳定裕度序列采取多步预测的方法。选取摔倒过程的稳定裕度样本N为1800，预测步长L为3。

图8 稳定裕度预测结果

稳定裕度的预测曲线和原始曲线如图8中所示，红色表示稳定裕度的预测值，灰色表示真实值，从图中可以看出预测曲线的拟合度可以达到93.2%。

4 结论

1) 分析摔倒过程中的运动学特征，采用足底压力中心点代替ZMP的方法确定人体稳定性的量化判别方法。

2) 通过摔倒过程中稳定裕度的自相关、偏相关系数，以及AIC判别准则，确定时间序列模型的类型和阶数；采用最小二乘法对AR模型进行参数辨识，获得最优的AR预测模型。

3) 采用AR时间序列模型对摔倒过程进行预测，获得了比较好的预测曲线，为摔倒过程的稳定恢复控制策略研究提供了依据和基础。

[1]伊蕾．助行康复机器人控制策略研究[D]．哈尔滨：哈尔滨工程大学,2012．

[2]Nishiwaki,K．and Kagami,S． Strategies for Adjusting the ZMP Reference Trajectory for Maintaining Balance in Humanoid Walking [C]．Proceedings of IEEE International Conference on Robotics and Automation,2010：4230-4236．

[3]Li．Q,Stankovic,J．A,Hanson,M．A, Barth．A．T,etc．Accurate．fast fall detection using gyroscopes and accelerometer-derived posture information[C]．In Proceedings of Sixth International Workshop on Wearable and Implantable Body Sensor Networks, Charlottesville,2009：138-143．

[4]佟丽娜,宋全军,葛云建．基于时序分析的人体摔倒预测方法[J]．模式识别与人工智能,2012,25/2：273-279．

[5]Q．Huang, K．Yokoi,S．Kajita,etc． Planning Walking Patterns for a Biped Robot [J]．IEEE Transaction on Robotics and Automation．2001：280-289．

[6]Peng Zhaoqin,Cao Chun,Huang Jiaoying．Human Moving Pattern Recognition toward Channel Number Reduction Based on Multipressure Sensor Network[J]．International Journal of Distributed Sensor Networks,2013．

[7]徐慧娟．自回归AR模型的整体最小二乘分析研究[D]．南昌：东华理工大学,2012．

[8]Peter J．Brockwell,Richard A．Davis． Time Series：Theory and Methods[M]．Second Edition．Beijing：China Higher Education Press,2007：130-151．