兰新高速铁路弓网系统动态接触电阻模型研究

赵施林



兰新高速铁路弓网系统动态接触电阻模型研究

赵施林

以动态接触压力、机车速度和牵引电流为主要输入变量，结合兰新高铁动车组实际运行环境，建立了动态接触电阻模型。分析了动态接触压力、机车速度和牵引电流在实际工况下的内部关系以及以弓网接触表面主要温升来源和动态接触电阻表征接触电阻的动态特性，并基于先进的高速铁路供电安全检测监测系统（CPCM和CCLM），采用差分进化算法对高速滑动温升模型和平均动态接触压力模型进行参数辨识，进而得出动态接触电阻模型，由此在机车3种运行状态下分析其动态接触特性。研究表明：速度和动态接触压力成为影响接触电阻大小最重要的因素，基于与实际运行的兰新高铁动车组同型号的高速综合检测车为实验载体建立的模型更加贴近实际工况。

兰新高速铁路；弓网系统；温升；动态接触电阻

0 引言

贯穿西北三省（甘肃、青海、新疆），世界上一次性建成通车里程最长的高速铁路—兰新高速铁路于2014年底正式通车。作为电气化铁路机车受流的唯一来源和重要三大核心关系之一的受电弓和接触网之间的接触（简称弓网接触）是电气化列车可靠、安全运行的基础。随着列车运行速度进一步提高，对机车电能的可靠传输提出了更高要求。对弓网接触而言，弓网振动、弓网结构柔性变形、接触线不平顺（硬点）等因素引起弓网磨损、弓网离线（产生电弧）等现象在高速铁路运营中时常发生，这将直接影响和制约机车受流系统的可靠性与稳定性。接触电阻作为弓网接触的一个基本参数，是衡量受流质量的重要指标，具体表现为接触电阻的阻值和稳定性，直接表征弓网接触受流质量和使用寿命。一方面，高速滑动虽然使磨损处于稳定的自润滑（低磨损）状态，但会导致弓网离线率的增加，以电弧热的方式加热并腐蚀弓网接触面；另一方面，大电流或过大的接触电阻会以焦耳热效应方式提升弓网接触部分的温度，直接影响接触线和滑板的物理性能。

1 弓网动态接触研究现状

弓网接触是一个动态关系，主要表现为：（1）弓网接触是典型的电接触，接触电阻在微观方面的物理机理为电流流过实际接触导电斑点产生的收缩电阻，在交流50 Hz工频以及大电流的工况下，会产生集肤效应，这是以牵引电流（）为主要表征参数的电接触理论；（2）弓网滑动接触产生摩擦热的同时，摩擦系数受温度和动态接触力等因素影响处于动态变化中，这是以速度（）和摩擦系数为主要表征参数的摩擦学理论；（3）在列车高速运行中，受电弓对接触线的抬升以及动态接触力受空气阻力和行车速度等因素的影响引起弓网振动，这是以动态接触力（）为主要表征参数的力学理论。上述3个方面以摩擦热、焦耳热和电弧热的形式构成动态弓网接触的主要温升来源。综上所述，动态弓网接触是一个以温度为强耦合参数的电、摩擦、力、热之间的耦合。

目前对弓网接触载流动态特性的研究主要集中在弓网系统载流磨损、动态接触热/传热模型及接触电阻等方面。载流磨损方面，文献[1～5]分别研究了高速、大接触压力、大电流、交流、弓网振幅以及电弧侵蚀对弓网系统磨损的影响，表明纯碳滑板更容易产生电弧放电；文献[6]充分考虑了摩擦热、焦耳热和电弧热，建立了弓网磨损模型；动态接触热/传热[7]方面，文献[8～10]建立了弓网接触面的稳态热模型，分别用来表征接触线、受电弓界面的温升；在接触电阻研究方面，文献[11]给出了静态接触电阻的表达式，表明接触压力与接触电阻呈反相关关系；在实际工况中，动态接触压力是一个包含风载、静态接触压力和其它力的矢量和[12]，当和一定时，引入载流效率和载流相对稳定系数求解最优接触压力[13，14]，发现载流效率随速度的增大而减小；文献[15～17]定量分析了弓网系统电接触特性，发现接触电阻与呈正相关关系，且在无载流时，硬度与收缩电阻成正比；文献[18]发现接触电阻随时间呈周期性波动，由此可知接触电阻的动态效应明显；温度变化是接触电阻动态效应的一个重要体现；文献[19]对热接触电阻的研究作了综述和展望；文献[20，21]建立了动态接触电阻模型，表明电流的增大会引起接触电阻的增大，该结论与文献[16]的结论相反；微观方面，文献[22，23]在阐述弓网接触特性时重点考虑了接触面的表面结构和外观特性。

然而，上述对接触电阻的研究所搭建的实验平台多为旋转式，其缺点是接触载荷波动较大[24]，同时考虑到接触线为“之”字形架设，加之列车的运行速度较高，对弓网接触面温升的冷却作用无法在现有的实验装置中实现，导致计算温升远远超出列车运行时弓网接触面的实际温升。同时，搭建的以电流、速度和接触力为主要输入变量的接触电阻模型忽略了该3个变量在机车运行中的内在动态关系。基于上述缺陷，本文充分考虑了兰新高速铁路的基本牵引环境，以、和为基本参数，建立了弓网动态接触模型。其中，以温度作为耦合参数，以温升模型为主线，充分考虑了电流、速度贡献的摩擦热和焦耳热。最后，采用国内先进、高效的高速铁路供电安全检测监测系统（下文简称6C系统），以高速综合检测车为实验载体，对、和以及接触面最高温度进行实时监测，并对模型参数进行校准，使建立的模型更加贴近实际工况。

2 动态接触电阻的数学模型

2.1 动态接触电阻数学模型的推导

根据弓网接触的物理机理，在直流工况下，弓网系统接触电阻由收缩电阻和膜电阻组成，即[25]

dc0=s+f（1）

式中，dc0为常温下的接触电阻，W；s为收缩电阻，W；f为膜电阻，W。

一个接触元件的收缩电阻可以表示为[26]

式中，w为接触线的电阻率，Ω·m；a为受电弓滑板的电阻率，Ω·m；为弓网接触区内导电斑点的半径，10-6m。

假设弓网接触区内导电斑点的形状为圆形，根据维氏硬度的定义，有

式中，为硬度较小（受电弓滑板）接触材料的洛氏硬度；为接触压力，N；为斑点数，令= 1，则可以表示为导电斑点的半径。

实际工况中，有一层覆盖弓网接触表面的表面污染膜，且污染膜的电阻率大于金属电阻率，形成的电阻称为膜电阻，可以表示为[27]

式中，f为薄膜电阻率，W·m；f为薄膜厚度， 10-6m。

弓网接触电阻对温度变化敏感，电阻随温度变化呈如下关系[9]：

式中，为电阻温度系数，1/K；Δ为温升，K。

考虑到兰新高铁设计速度为200～250 km/h，弓网属于高速滑动接触，其温升可以表示为[28]

因接触线为“之”字形架设，接触线与受电弓的接触为非永久性接触状态，考虑行车速度对弓网接触温度的冷却作用，引入一个冷却系数，即

=· (f+j) （7）

式中，f为滑动摩擦热流密度，J；j为焦耳热密度，J。可以分别表示为

f=（8）

j=2ac0（9）

式中，为摩擦系数。

因受电弓的静态接触力可调范围为50～ 120 N，隧道内导电膜电阻率af取值为2.75× 10−14W·m2，将其代入式（3）、式（4）中可得膜电阻的范围为[8.83×10−8，2.12×10−7]W，即在高速滑动过程中覆盖在弓网接触表面的薄膜被磨损，导致膜电阻的阻值非常小，此时可以忽略。

2.2 动态接触力模型

列车在运行过程中，任意时刻的接触力等于静态接触力0、空气动力a、受电弓铰接部位的摩擦阻力f和动态接触分力d的矢量和[29]，即

=0+a+f+d（10）

弓头向上运动时，出现动态接触力最小值，即

min=0+a-(çf÷+çd÷) （11）

弓头向下运动时，出现动态接触力最大值，即

max=0+a+ (çf÷+çd÷) （12）

故平均动态接触力ave为

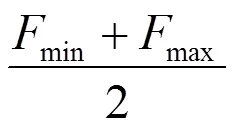
式中，0为升/降弓时静态接触力的平均值；a与的平方呈正比，即

a=2（14）

式中，为与受电弓弓头高度和运行位置无关的恒定系数。

3 实验系统与材料

该实验采用全方位、全覆盖的6C系统，6C系统由高速弓网综合性能检测系统（Comprehensive Pantograph and Catenary Monitor Device，CPCM）、接触网运行状态检测系统（Catenary-Checking on-Line Monitor Device，CCLM）等6个子系统组成。其中，CPCM的主要功能为对接触网参数（动态导高、拉出值）和弓网实时运行状态（弓网动态接触压力、接触线的硬点、弓网离线电火花、行车速度和公里标）进行综合检测；CCLM的主要功能为测量接触网动态几何参数（动态导高、拉出值）和采集弓网运行中最高温度。

采用CPCM和CCLM分别对行车速度、电流（由机车监控系统提供）、动态接触力（包括最大动态接触力、最小动态接触力和平均动态接触力）和弓网接触温度进行实时采集。实验载体为高速综合检测列车（Comprehensive Inspection Train，CIT）（牵引系统一般采用10个550 kW电机，其额定功率为5 500 kW，接触网电压为27.2 kV），采集区段为嘉峪关南站—哈密站（该区段路面平滑，无2‰坡道）。在实时采集过程中，还应注意以下几点：

（1）CPCM和CCLM的采集应保持在同一时间，同一区段；

（2）去除太阳与红外热相仪对射时间段内影响温度采集精度的数据；

（3）行车速度低于60 km/h，采集的最高温度未出现在弓网接触表面，故去除速度低于60 km/h时采集的温度数据。

兰新高铁采用CTS150型铜锡合金接触线和DSA250.30型纯碳滑板，其相应参数见表1和表2。

表1 接触线基本参数

表2 受电弓的物理参数

4 实验结果与分析

4.1 参数F、V和I的相互关系

对于兰新高速铁路，一般在190～200 km/h范围内，由于测试路段无2‰坡道，在实际测试过程中，在190～194 km/h范围内的概率较大，稳定在一个轻微波动范围内。

的大小取决于机车牵引力的大小。机车在加速过程或处于上坡阶段，牵引力增大，电流也随之增大；机车在制动过程中（包括下坡制动），牵引力为负，值非常小。根据兰新高铁机车监控系统的显示，机车从静止到最大速度过程中，增大，其最大值max= 260 A，当速度提升至稳定速度时，机车牵引力稳定在20 kN，稳定在100 A左右。

综上，机车运行稳定后，和的值保持稳定，可以视为常量。由于的引入导致弓网振动，动态接触力随时间不断变化。图1表示了在某一段时间内采集的动态接触压力变化曲线。

与0、和弓网振动振幅有关。通过CPCM实时采集的数据对表达式中模型未知参数进行辨识。

图1 平均动态接触压力随时间变化曲线

4.2 F模型未知参数辨识

图2 平均动态接触力与行车速度的关系

为了验证辨识参数的可靠度，表3给出了兰州铁路局兰西动车所测得的升弓状态下弓网静态压力的测试数据。由此计算出升弓状态下弓网平均静态压力为86.533 N，结合所辨识出0的值计算出降弓状态下弓网平均静态压力为93.447 N，其值满足受电弓升起状态（一级检修）标准：弹簧秤匀速向下运动时（降弓），压力不大于95 N（93.447 N），弹簧秤匀速向上运动时（升弓），压力不小于65 N（86.533 N）。验证了模型的可靠性。

表3 升弓状态下弓网静态压力的测试数据 N

4.3 弓网接触温升模型参数辨识

基于CCLM系统在不同速度、电流下实时采集的弓网接触表面最高温度/温升，根据机车在稳定状态下电流和速度恒定的原理，将采集的最高温度/温升、电流和速度代入式（6）—式（9），计算出冷却系数。图3和图4分别为CCLM系统采集的弓网接触实物图和红外热成像图。

图3 弓网接触实物图

图4 弓网接触红外热像图

机车稳定运行时，采集17：10到17：24时间段内数据，见图5。据图5可知，在17：13：20时刻，由于极短暂的弓网离线导致温升达到最大值108℃（在其他时刻，如17：11：20，温升29℃），由于接触网不平顺等因素导致温度骤升；在17：13：40—17：21：00时间段内，无弓网离线及接触网不平顺等影响因素，温度达到稳定状态。在实际计算中，去除弓网离线和接触网不平顺因素对温度影响的数据，求其平均值（7.98℃）作为最终温升。

由此，将= 100 A，= 192 km/h，Δ= 7.98℃代入式（6）—式（9），解得= 0.174 2。

图5 弓网接触面温升随时间的变化曲线

4.4 弓网接触电阻特性

结合上述参数辨识结果，采用Maple 2016软件，代入式（1）—式（9）可得在某一接触温度下，弓网动态接触电阻为

ac= 0.357 2×-0.5+ 0.00 022×0.5·-0.25+ 0.000 5×-1.75·2（15）

当= 0时，静态接触力0与静态接触电阻dc0的关系如图6所示。由图可知，随着0的增大，静态接触电阻减小。

图6 静态接触电阻随静态接触力的变化曲线

当≥0时，即机车处于动态，此时将机车的运行状态分为3个阶段：加速阶段、制动阶段和稳定阶段。当机车由静止开始加速时，机车牵引力逐渐增大，此时在短时间内达到最大值（max= 260 A）并保持稳定；当速度增加至194 km/h时，加速阶段结束，由此进入稳定阶段，在该阶段速度能够保持在190～198 km/h，此时稳定在100 A；当机车处于下坡制动或减速状态时，牵引力为负值，非常小，维持在0～40 A，取值为max= 30 A。在该过程中，不断变化，将的变化量（0～ 198 km/h）代入式（13）、式（14）中算出平均动态接触力ave的范围：89.99 N≤ave≤142 N。图7表示机车在加速（= 260 A）和制动状态（= 30 A）下动态接触电阻dc随ave和变化的三维曲面图，可以看出，dc随ave的增大而减小，随、的增大而增大。

图7 加速和制动状态下Rdc随Fave和V变化的三维曲面图

图8为机车在稳定状态下dc随ave和变化的三维曲面图。由图可知，在稳定状态下，dc随ave和变化较小（0.5 mΩ），考虑弓网振动导致动态接触力变化幅度较大，例如，在机车稳定时的高频状态下，ave= 139 N时（= 192 km/h），测得min= 86 N，max=191 N。代入式（10），计算得最大接触电阻dcmax= 0.039 1W，dcmin=0.026 2W。

图8 稳定状态下Rdc随Fave和V变化的三维曲面图

5 结论

（1）机车在持续加速时，焦耳热占弓网接触温升的比重为66%～94%，为主要温升来源；机车处于持续制动状态时，摩擦热占弓网接触温升的比重为75%～95%，为主要温升来源。

（2）在影响弓网系统接触电阻的3个参数中，的大小与0（已知）、、弓网振动振幅和受电弓型号有关，已知，为非大电流（轻载），故和弓网振动振幅成为影响dc的主要参数。

（3）弓网接触温升模型的参数辨识中引入差分进化算法，具有良好的全局搜索能力以及特殊而又简单的进化原则，辨识性能优于其他进化算法。

（4）交流频率成为影响弓网接触电阻的一个重要参数，当频率高于100 kHz时，集肤效应显著。但对于工频为50 Hz的低频交流供电系统的弓网接触电阻，笔者研究团队正在做后续研究。

[1] Ding T, Chen GX, Wang X, et al. Friction and Wear Behavior of Pure Carbon Strip Sliding Against Copper Contact Wire Under AC Passage at High Speeds[J]. Tribology International, 2011, 44(4): 437-444.

[2] Siopis MJ, Neu RW. The Effect of Tribomaterial Pairings on Wear of an Aluminum Slider Under High Sliding Speeds and High Contact Pressure[J]. Wear, 2016, 352-353(2016): 180-187.

[3] Argibay N, Sawyer WG. Low Wear Metal Sliding Electrical Contacts at High Current Density[J]. Wear, 2012, s 274–275(3): 229-237.

[4]陈伟，陈光雄，李红，等. 弓网振幅对纯碳及浸金属碳滑板载流摩擦磨损性能的影响[J]. 润滑与密封，2015，40（9）：25-29.

[5] Ding T, Chen GX, Li YM, et al. Arc Erosive Characteristics of a Carbon Strip Sliding Against a Copper Contact Wire in a High-speed Electrified Railway[J]. Tribology International, 2014, 79(11): 8-15.

[6] Bucca G, Collina A. Electromechanical Interaction Between Carbon-based Pantograph Strip and Copper Contact Wire: A Heuristic Wear Model[J]. Tribology International, 2015, 92(2015): 47-56.

[7] Raghupathi PA, Kandlikar SG. Contact Line Region Heat Transfer Mechanisms for an Evaporating Interface[J]. International Journal of Heat & Mass Transfer, 2016, 95(2016): 296-306.

[8] Plesca A. Thermal Analysis of Sliding Electrical Contacts with Mechanical Friction in Steady State Conditions[J]. International Journal of Thermal Sciences, 2014, 84(84): 125-133.

[9] Nituca C. Thermal Analysis of Electrical Contacts from Pantograph-Catenary System for Power Supply of Electric Vehicles[J]. Electric Power Systems Research, 2013, 96(2013): 211-217.

[10] Gao S, Wang Y, Liu Z, et al. Thermal Distribution Modeling and Experimental Verification of Contact Wire Considering the Lifting Or Dropping Pantograph in Electrified Railway[J]. IEEE Transactions on Transportation Electrification, 2016, 2(2): 256-265.

[11] Wang W, Dong A, Wu G, et al. Study on Characterization of Electrical Contact Between Pantograph and Catenary[C]// 2011 IEEE 57th Holm Conference on Electrical Contacts, Journal of Applied Physics, Minnesota, USA, IEEE, 2011: 1-6.

[12] Jürgens P, Wetzel T, Schieferstein H, et al. Influence of the Aerodynamic Forces on the Pantograph–catenary System for High-speed Trains[J]. Vehicle System Dynamics, 2009, 47(11): 1327-1347.

[13] 胡艳，董丙杰，黄海，等. 碳滑板/接触线摩擦磨损性能[J]. 交通运输工程学报，2016，16（2）：56-63.

[14] 陈忠华，唐博，时光，等. 弓网多目标滑动电接触下最优压力载荷[J]. 电工技术学报，2015，30（17）154-160.

[15] C. weißenfels, P. wriggers. Numerical Modeling of Electrical Contacts[J]. Computational Mechanics, 2010, 46(2): 301-314.

[16] 吴杰，高国强，魏文赋，等. 弓网系统滑动电接触特性[J]. 高电压技术，2015，41（11）：3635-3641.

[17] 朱宁俊，李春茂，吴广宁，等. 弓网系统接触电阻特性的研究[J]. 铁道科学与工程学报，2015，12（5）：1185- 1190.

[18] Wu G, Wei W, Gao G, et al. Evolution of the Electrical Contact of Dynamic Pantograph–catenary System[J]. Journal of Modern Transportation, 2016, 24(2): 132-138.

[19] Wang AL, Zhao JF. Review of Prediction for Thermal Contact Resistance[J]. Science China Technological Sciences, 2010, 53(7): 1798-1808.

[20] 李春茂，朱宁俊，吴广宁，等. 弓网系统动态接触电阻数学模型的研究[J]. 高电压技术，2015，41（11）：3554-3560.

[21] 陈忠华，石英龙，时光，等. 受电弓滑板与接触网导线接触电阻计算模型[J]. 电工技术学报，2013，28（5）：188-195.

[22] Zhou N, Zhang WH, Li RP. Dynamic Performance of a Pantograph-catenary System with the Consideration of the Appearance Characteristics of Contact Surfaces[J]. Journal of Zhejiang University-science (Applied Physics & Engineering), 2011, 12(12): 913-920.

[23] Holzapfel C. Contact Surfaces for Sliding Electrical Contacts[C]// 2014 IEEE 60th Holm Conference on Electrical Contacts, Journal of Applied Physics, San Diego, USA, IEEE, 2015: 1-7.

[24] Chikara yamashita, 周贤全. 接触导线与滑板在电流条件下的磨损模式[J]. 国外铁道车辆，2016，53（3）：35-39.

[25] Holm R. Electric Contacts: Theory and Application[M]. Boca Raton: CRC Press, 2013. 3-104.

[26] Holm R. Electric Contacts: Theory and Application; with 218 Fig[M]. Stockholm: Springer-Verlag Berlin Heidelberg GmbH 1967. 3-102.

[27] Braunovic Milenko, Konchits Valery-V, Myshkin Nikolai-K. 电接触理论，应用与技术[M]. 北京：机械工业出版社，2010. 1-32.

[28] Boubechou C, Bouchoucha A, Zaidi H, et al. Thermal and Tribological Analysis of the Dry Sliding Steel-steel Couple Traversed By an Electrical Current[J]. Physics Procedia, 2014, 55(2014): 165-172.

[29] 吴积钦. 受电弓与接触网系统[M]. 成都：西南交通大学出版社，2010：36-44.

The dynamic contact resistance model is established with dynamic contact force, locomotive speed and traction current as main variables, with connection of actual operation environment of electric multiple unit of Lanzhou-Xinjiang high speed railway. The paper analyzes internal relations of dynamic contact forces, running speed of electric locomotive and traction current under actual operation conditions, sources of temperature-rise on contact surface between pantograph and catenary as well as dynamic characteristics of contact resistance represented by dynamic contact resistance. The dynamic contact resistance model is obtained through parameter identification for high speed sliding temperature-rise model and average dynamic contact force model, on the basis of advanced power supply safety inspection and monitoring system (CPCM and CCLM) for high speed railway; and from this, the paper further analyzes dynamic contact characteristics of electric locomotive under three operation modes. The research results show: the train running speed and dynamic contact forces are becoming main factors affecting the contact resistance value. And the established model, with a high speed integrated inspection car whose model is identical to that of EMU for Lanzhou-Xinjiang high speed railway as the experimental carrier, is more close to the actual operation conditions.

Lanzhou-Xinjiang high speed railway; catenary-pantograph system; temperature-rise; dynamic contact resistance

10.19587/j.cnki.1007-936x.2017.05.011

U225.3

A

1007-936X(2017)05-0046-07

赵施林.兰州铁路局嘉峪关供电段，高级工程师。

2017-01-13