一种基于新共轭梯度方法的滑动平均模型参数估计优化法

(燕山大学理学院 河北 秦皇岛 066004)

一种基于新共轭梯度方法的滑动平均模型参数估计优化法

王美霞

(燕山大学理学院河北秦皇岛066004)

基于非线性规划的共轭思想，结合不同的共轭梯度法的优势，给出新的参数标量以及搜索方向，从而提出一种改进的共轭梯度法，并给出全局收敛性的证明。考虑将模型参数估计转换成无约束优化问题，然后利用改进的共轭梯度法来修正原始的ARMA(p,q)模型的参数估计值，从而提高模型的预测精度，并给出数值算例，来验证改进方法的有效性。

非线性规划；共轭梯度法；全局收敛性；ARMA(p,q)模型；参数估计

在时间序列的统计分析中，平稳时间序列是一类重要的随机序列，最常用的就是ARMA(p,q)模型，全称是自回归移动平均模型，简单记为ARMA(p,q)模型[1]是目前最常用的拟合平稳序列的模型。1927年，英国统计学家G.U.Yule首先提出自回归(autoregressive，AR)模型[2]。 1970年，Box与Jenkins联合发表了专著《时间序列分析：预测和控制》[3]对时间序列方法以及应用做了系统并且深入的论述。2003年，针对参数问题，熊渊博[4]提出了对ARMA(p,q)模型的参数进行分步估计的方法，此方法通过对AR(p)模型的两次估计来达成ARMA(p,q)模型的参数估计，再利用实例证明该方法的有效性；2009年，范菁[5]针对如何提高模型的拟合精度的问题，提出了三参数共轭梯度法，该方法是在原始共轭梯度法的原理上引入参数标量来确保迭代步长不小于零；同一年，郑彩萍[6]等人将非线性时序模型的参数估计法中融入了阻尼最小二乘法，提出了对于原始模型的参系数的改进方法，通过对t统计量的求解来验证改进方法的有效性。

本文在现有文献的基础上，结合非线性规划中的共轭思想，优化ARMA(p,q)模型中的参数估计，提出一种新的共轭梯度法：MHS-DY法。

一、MHS-DY法

(一)共轭梯度法

对于无约束优化问题

minf(x),x∈Rn

(1)

函数f:Rn→R1是连续可微的。

共轭梯度法是介于最速下降法与牛顿法之间的一种方法，不仅避免了最速下降法收敛速度慢的缺点，还克服了牛顿法求海赛矩阵的不足，还具有二次终止性，因此在求解上述无约束优化问题时，共轭梯度法更为合适，此方法尤其适合求解维数n较大的问题。主要迭代格式如下所示：

xk+1=xk+αkdk

(2)

其中，αk为步长因子。dk为下降搜索方向。βk为标量，标量参数不同产生的共轭梯度法不同。 常见的共轭梯度法算法有：FR算法，DY算法，HS算法，PRP算法。其中，FR算法与DY算法收敛性较好，但是数值表现并没有HS和PRP算法好，文献[5]提出使参数的标量满足：

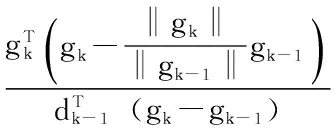
(3)

将该方法记为MHS算法，本文将结合MHS算法以及DY算法的优越之处构造出一种新的组合优化方法即MHS-DY法。

(二)MHS-DY法

针对前文中提到的无约束优化问题(1)，引用文献[5]中提到的含参数的共轭梯度法思想，公式(3)作为参数标量，再结合DY算法的全局收敛性优势，提出MHS-DY法：

(4)

其中

保证搜索方向为下降方向，综合考虑搜索方向：

(5)

式中，dk满足下降方向，并且不依赖任何线搜索。

二、基于新MHS-DY法的模型参数优化算法

(一)目标函数的确定

ARMA(p,q)模型结构为：

Xt-φ1Xt-1-...-φpXt-p=εt-θ1εt-1-...-θqεt-q

移项

Xt=φ1Xt-1+…+φpXt-p+εt-θ1εt-1-…-θqεt-q

记为

其中

ω=[φ1，φ2，…φp,-θ1,-θ2,…-θq]T

考虑到ARMA(p,q)模型中Xt与ω之间是非线性关系，定义目标函数为模型的残差平方和：

(6)

由无约束优化理论的数学模型得知，估计模型的参数ω的问题就转变成求使得S(ω)达到极小值的最优解ω*。

(二)初值的确定

本文采取的是AP(p0)长自回归模型，其计算原理是：以模型的等价系统传递函数为入手点，同时将逆函数的概念加入其中，并运用待定系数法得到如下公式：

(7)

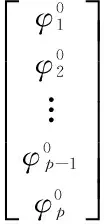
(8)

(9)

(三)参数估计步骤

1)对于ARMA(p,q)模型，令p+q=m，参数初值结构如下：

(10)

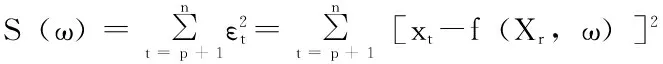
(11)

其中，

(12)

(13)

记为矩阵形式如下：

(14)

因此S0=S(ω0)，初始搜索方向d0=-g0，令k=0。

3)如果‖gk+1‖<ε，那么ωk+1就是极小值点，否则，进行下一步。

4)若k=p，则ω0=ωk+1,S0=Sk+1,g0=gk+1,d0=-g0,k=0，然后转向2)；否则，转向5)。

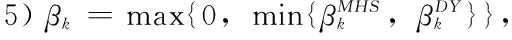
6)若(dk+1)Tgk+1≥0，则重复操作4)，转向2)；否则，k=k+1，转向2)。

三、收敛性分析

假设：(1)水平集Ω={∈Rn|f(x)≤f(x0)}有界。

(2)函数f在Ω的某个邻域Φ内连续可微，并且g(x)满足利普希茨连续条件，即∃L>0，使得下式成立：

‖g(x1)-g(x2)‖≤L‖x1-x2‖,∀x1,x2∈Φ

(15)

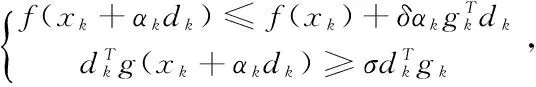
(16)

用反证法证明上述定理如下：

证明：假设结论不成立。已知∀k>0,∃ε>0,ε为常数，使(17)式成立

‖lk‖≥ε

(17)

由

(18)

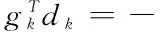
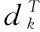
(19)

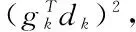
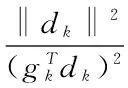
由此得出：

(20)

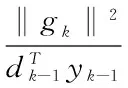
四、实例分析

MHS-DY算法经数值算例证实其在求解无约束问题时同样保持了良好的数值结果及收敛性，可将ARMA(p,q)模型的参数优化问题转换成无约束优化问题进一步求解，本文引用文献[5]中的算例(数据如表1所示)进一步检验本文算法的实用性。前100个数据用于模型的预测，101～103用于模型检验，利用MHS-DY算法对ARMA(1,1)模型进行参数估计，此时，初值β0=(1,0.5)，令δ=0.01，σ=0.1，同时利用Matlab[12]软件做编程，经过五次迭代后结果如下：

ω5=(0.8673,0.4898)T

模型结构为：

xt=0.8673xt-1+εt-0.4898εt-1

利用MHS-DY算法改进后的参数模型预测结果见表2

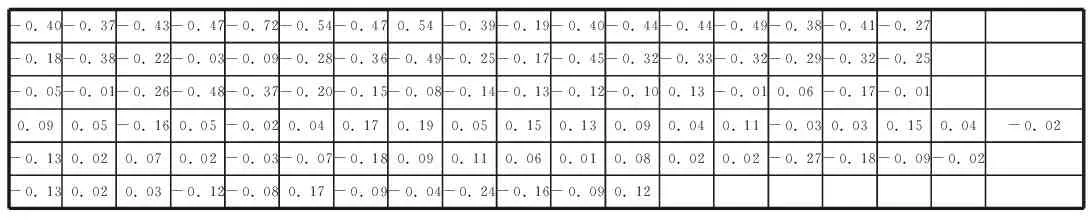
表1 平稳序列

表2 预测结果对比

注：n 的值表示平稳序列中第n个数。

五、结论

本文的核心思想是将模型的参数估计问题转换成无约束优化问题进行研究，参考文献[5]的思想上提出了一种新的共轭梯度法MHS-DY算法并运用该算法优化ARMA(p,q)模型参数，详细的证明了此方法具有全局收敛性以及充分下降性。最后，用实例进行验证分析，结果表明优化后的模型有更好的拟合效果。

[1]王燕.应用时间序列分析[M].北京:中国人民大学出版社,2005.145-147.

[2]S.Andreas.Weigend and A.Neil Gershenfeld.Time Series Prediction:Forecasting the future and Understanding the Past,eds.Reading,MA:Addison-Welsley,1993

[3]G.E.P.Box,G.N.Jenkins and G.C.Reinsel著.时间序列分析预测与控制.顾岚主译.北京:中国统计出版社,1997:45-49

[4]ARMA模型参数的分步估计方法[J].湖南大学学报(自然科学版),2003,30(2):12-13.

[5]范菁.ARMA模型的两种共轭梯度参数估计法及ARIMAX模型的应用[D].燕山大学,2009.

王美霞(1991-)，女，汉族，河北唐山人，硕士，燕山大学，最优化理论。

)