六自由度轻型机械臂的运动误差分析

，

(北京林业大学工学院，北京 100083)

研究与设计

六自由度轻型机械臂的运动误差分析

李亚奇，肖爱平*

(北京林业大学工学院，北京 100083)

轻型机械臂广泛应用于各个领域，其有许多优点，但也存在一些问题，如刚度低、易产生柔性变形等。建立了机械臂的运动误差模型，分析了其在弹性变形时产生的误差，同时讨论了减小误差、提高末端精度的方法。

轻型机械臂；误差模型；运动误差；柔性误差

轻型机械臂在我们的日常生产、生活中发挥着越来越重要的作用，其具有许多优点，如质量轻、功耗低、操作灵活、运输方便等，但也存在刚度较低，容易产生柔性变形等问题，这样就使得轻型机械臂末端的位置和姿态误差较大，定位精度较低。

机械臂的运动误差是衡量机械臂性能的重要指标之一，目前在计算机械臂的运动时一般是假设构件为刚性体，各个运动副之间都是零误差的理想状态来构建模型，但实际应用中构件往往会发生变形，构件的柔性会对系统的运动过程产生影响，如果不考虑构件的柔性，在运动学分析中就会产生很大的误差。本文采用D-H参数法来分析机械臂的运动误差[1]。

1 坐标系的建立

机械臂的构型如图1所示，根据构型建立的各连杆坐标系如图2所示，相应的连杆参数见表1。利用齐次变换矩阵表示相邻两个坐标系之间的相对位姿和运动关系，将这些矩阵依次相乘得到的变换矩阵就是末端坐标系相对于基坐标系的齐次变换矩阵。

图1 机械臂构型

图2 各连杆坐标系

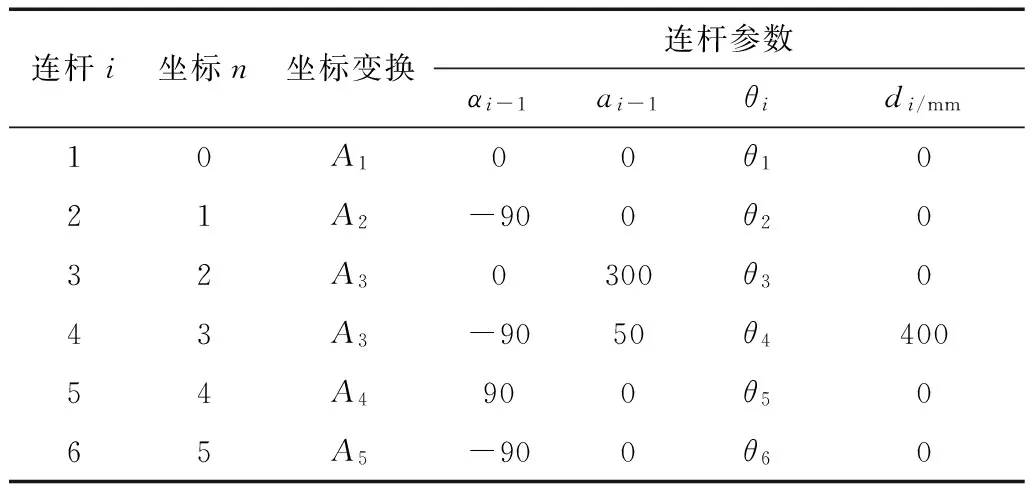
表1 连杆参数

连杆i坐标n坐标变换连杆参数αi-1ai-1θidi/mm10A100θ1021A2-900θ2032A30300θ3043A3-9050θ440054A4900θ5065A5-900θ60

表中：αi-1为从Zi-1到Zi绕Xi-1旋转的角度；ai-1为从Zi-1到Zi沿Xi-1偏移的距离；di为从Xi-1到Xi沿Zi偏移的距离；θi为从Xi-1到Xi绕Zi旋转的角度。

2 微分运动

(1)

因此，第i个杆件相对于末端坐标系的变换矩阵Ti等于各变换矩阵右乘。从而得到的结果如下：

末端执行器的变换矩阵为：

变换矩阵可表示为：

(3)

nx6=C1[C23(C4C5C6-S4S6)-S23S5C6]

+S1(S4C5C6+C4S6)

ny6=S1[C23(C4C5C6-S4S6)-S23S5C6]

-C1(S4C5C6+C4S6)

nz6=-S23(C4C5C6-S4S6)-C23S5C6

ox6=C1[C23(-C4C5S6-S4C6)+S23S5S6]

+S1(C4C6-S4C5S6)

oy6=S1[C23(-C4C5S6-S4C6)+S23S5S6]

-C1(C4C6-S4C5S6)

oz6=-S23(-C4C5S6-S4C6)+S23S5C6

ax6=-C1(C23C4S5+S23C5)-S1S4S5

ay6=-S1(C23C4S5+S23C5)+C1S4S5

az6=S23C4S5-C23C5

px6=C1[300C2+50C23-400S23]

py6=S1[300C2+50C23-400S23]

pz6=-50S23-300S2-400C23

式中：Cn=cosθn，Sn=sinθn，C23=C2C3-S2S3，S23=C2S3+S2C3

假设机械臂的第i根杆件发生弹性变形的坐标系统相对于没有发生弹性变形坐标系统的微分变化为：

式中：di为第i根杆发生的微分位移；δi为第i根杆发生的微分旋转。

现在假定只有第i根杆件发生了微变形，其余的杆件均保持不变，则这根杆件引起末端坐标系的微分变化为：

(4)

式中：JΔ为第i根杆件的坐标系与末端坐标系的微分转换方程，[2]其表达式为：

(5)

通过式(1)～(5)可以求出末端的微分变化，再将其进行叠加就可以得到微分变化下末端坐标系总的位置和姿态的误差，表达式为：

6δx=(C1δx1+S1δyi)+(C1C2δx2+S1C2δy2-S2δz2)

+(C1C23δx3+S1C23δy3-S23δz3)

+[(C1C23C4-(-C1S2-S1)S4)δx4+(S1C23C4

-(-S1S2+C1)S4)δy4+(-S23C4+C2S4)δz4]

+[((C1C23C4-(-C1S2-S1)S4)C5-C1S23C5)δx5

+((S1C23C4-(-S1S2+C1)S4)C5-S1S23C5)δy5

+((-S23C4+C2S4)C5-C23S5)δz5]

+[(C1(C23(C4C5C6-S4S6)-S4S6)-S23S5C6)

+S1(S4C5C6+C4S6))δx6+(S1(C23(C4C5C6

-S4S6)-S23S5C6)-C1(S4C5C6+C4S6))δy6

+(-S23(C4C5C6-S4S6)-C23S5C6)δz6]

由于6dx、6dy、6dz、6δy、6δz的表达式都很复杂，这里不再详细列出。

3 连杆柔性误差

在刚性机械臂中只需要考虑几何误差即可，但在柔性连杆中，不仅存在几何误差，同时还存在柔性误差。连杆的柔性对于机械臂的影响非常复杂，要想分析其产生的误差，首先要知道其在受力情况下是如何变形的。图3所示为梁受到均布载荷Q、集中作用力F及弯矩τ三种典型力的作用，当梁受到不同的载荷影响时，可以通过对不同载荷造成的变形进行叠加，从而得到总的变形量。图中l为梁的长度、θ为梁的末端转角，ω为梁末端的挠度[3-6]。

图3 梁的变形

在集中载荷F的作用下，末端的挠度和转角分别为：

式中：E为弹性模量，I为梁的截面惯性矩。同理，在其他载荷作用情况下的挠度和转角也可以求出。

图3所表示的只是连杆在平面内的受力情况，但实际情况下连杆受到的力往往是在空间范围内的，它引起的变形不仅产生位置误差，而且还会产生姿态误差。连杆受到空间力旋量作用示意图如图4所示。

图4 连杆受到空间力旋量作用示意图

将连杆一端固定，并在其上固连一个坐标系OXYZ，另一端为O′X′Y′Z′，其中O′X′Y′Z′是由OXYZ沿X轴平移得到的，在坐标系原点受到外力F=(fx,fy,fz,τx,τy,τz)T的作用时，利用有限元法对机械手进行分析，ei=Si·Fi。

式中：E为弹性模量，G为剪切模量，Iz为连杆截面相对于z轴的惯性矩，Iy为连杆截面相对于y轴的惯性矩，Ip为连杆截面相对于坐标系原点的极惯性矩，A为连杆的截面。

根据以上公式，忽略连杆自重引起的变形，可以得到连杆坐标系的弹性变形矢量，表达式为：

式中：ei为连杆坐标系i的弹性变形矢量；Si为连杆坐标系i的柔度矩阵；Fi为连杆i末端所受的外力矩阵。

将上式的弹性变形矢量转化到机械手末端坐标系中，可得：

式中：C为变换矩阵的旋转矩阵。

机械手末端的弹性变形为所有杆件的变形之和，则弹性变形的位置向量DN和方向向量ψN分别为：

式中：k=1，2…N。

根据以上的位姿误差模型，给出运动参数和对应的原始误差就可以求得机器人末端坐标系在杆件发生弹性变形时在绝对坐标系中的位置误差和姿态误差[7]。

4 减小运动误差的方法

机械臂误差产生的原因很多，因此要确定误差的变化规律有一定的难度，根据以上的理论和误差模型主要分析了由于杆件弹性变形引起的误差变化。在实际应用中可得到每个杆的变形量，然后带入相关公式即可得到机械臂末端的位置和姿态误差。

在实际工作中也可以通过以下方法来减小运动误差。

(1)软件补偿。通过控制软件进行补偿，从而减小运动误差的影响，提高机械臂的运动精度。

(2)通过实际测量结果与理论计算来分析误差产生的原因，明确哪些是系统误差、哪些是随机误差，对随机误差要通过最小二乘法来计算其均值，从而在实际的路径规划中减小这些误差的影响。

(3)在每个杆件上安装传感器来测量杆件的弹性变形，再通过控制器在每个关节中增加一个补偿量，以达到减小误差的目的。

(4)利用宏/微型机器人减小误差。在一个大的机械臂末端安装一个微型机器人，从而使整体的精度得到提高。

(5)选用质量轻、刚度好的材料来制造机械臂的杆件。

[1] 熊有伦.机器人学[M].北京：北京工业大学出版社，1992.

[2] 谭月胜，孙汉旭，肖爱平，等.模块化柔性臂空间机器人运动误差分析[J].机械设计，2004，9(21)：14-16.

[3] 张蔓，高宇博，李军，等.教学用双足步行机器人前向运动建模与研究[J].林业机械与木工设备，2017，45(5)：32-34+39.

[4] 杨红梅，熊晓航.RV-MI型机器人的误差分析[J].辽宁工学院学报，1999(3)：31-34.

[5] 王兴松.机器人柔性臂动态运动误差的实时测量[J].机械科学与技术，1997，26(5)：55-57.

[6] 韩晓建，杨卫杰，高寰宇，等.基于连杆机构的四足仿生机器人运动学分析及足迹优化[J].森林工程，2017，33(1)：52-58.

[7] 金仁成，赵继，杨红梅，等.RV-MI型机器人的运动误差分析[J].汽车工艺与材料，1999(11)：31-33.

AnalysisofMotionErrorsofSixDOFLightMechanismArms

LIYa-qi，XIAOAi-ping*

(College of Technology，Beijing Forestry University，Beijing 100083，China)

Light mechanisms are widely used in various areas，with many advantages，involving some problems as well like low stiffness and easy flexible deformation.A motion error model has been established for mechanical arms，with errors produced during elastic deformation analyzed and the methods to reduce errors and improve end precision discussed.

light mechanical arm；error model；motion error；flexible error

TM301；TP242

A

2095-2953(2017)11-0015-05

2017-07-01

李亚奇(1991-)，男，河北石家庄人，在读硕士研究生，研究方向为现代制造工艺及自动化装备，E-mail：1098085384@qq.com。

*通讯作者：肖爱平(1971-)，男，湖南株洲人，副教授，博士后，主要从事智能机器人的研究，E-mail：xxaapp@sina.com。

(责任编辑 张雅芳)