边攻击下非对称相依作战网络级联失效模型
韩海艳,杨任农,王 哲,宋晓鸥
(1.空军工程大学 航空航天工程学院,西安 710038;2.武警工程大学 信息工程系,西安 710086)
边攻击下非对称相依作战网络级联失效模型
韩海艳1,杨任农1,王 哲1,宋晓鸥2
(1.空军工程大学 航空航天工程学院,西安 710038;2.武警工程大学 信息工程系,西安 710086)
复杂网络理论在作战网络中的应用是一个全新的研究视角,也是探索网络结构和功能之间关系的有力手段.为研究负荷作用下相依作战网络的级联失效过程,首先依据军事系统的实际交联关系构建了非对称双层相依作战网络模型;然后改进了基于本地负荷重分配的非线性“负荷-容量”模型来研究连边的失效及负荷传递,计算了级联失效模型的计算复杂度;最后仿真分析了连边遭受蓄意攻击时,连边负荷及容量与网络级联抗毁性的关系,并与WS-WS对称网络模型进行对比.仿真结果表明:无论是孤立状态还是相依状态下,网络的级联抗毁性与连边容量变化呈正相关,而与负荷的变化呈负相关;相依网络的级联抗毁性比孤立网络要差,并且相依网络级联失效的过程更缓慢;孤立C2网络中的层级加权结构使得级联失效过程中出现短暂的平台期;与对称WS-WS相依网络相比,非对称作战网络的级联抗毁性更差.在非对称相依网络中,子网之间的级联抗毁性不同,而在相依对称网络中,子网的级联抗毁性几乎相同.
非对称相依作战网络;“负荷-容量”模型;边蓄意攻击;负载重分配;级联抗毁性
小世界网络[1]和无标度网络[2]模型的提出标志着网络科学进入了一个新时代,探索网络结构和网络整体功能之间的关系,成为各领域的研究热点.学界对复杂网络[3]的研究正逐步由无权、孤立网络向加权、相依网络方向[4-6]发展.网络的整体特性源于其组件之间的复杂交互作用.在现实世界中并不存在完全孤立的网络,一个网络都或多或少地与其他一个或多个网络存在耦合关系,例如电力网络和计算机网络相互依赖,一方面电力网络为计算机网络的正常运行提供了电力支持,另一方面计算机网络反过来又控制电力网络的发电运行,这种子网之间存在相互依赖关系的网络称为相依耦合网络.
级联抗毁性综合考虑了网络的结构及其动力学行为.2010年,Buldyrev等[7]发表在Nature上的一篇文章开启了相依网络级联失效研究的浪潮,当一个网络中的节点(边)故障时,将会影响到另一个网络中与其相互依赖的节点(边).研究成果表明,随机攻击下,相依网络中的级联故障更严重.Gao等[8]则对相互依赖关联网络的研究进行了全面综述.陈世明等[9]基于BA、WS、ER这3种基本网络模型,建立了对称和非对称相依网络模型,研究了网络级联抗毁性与耦合强度之间的关系.而这些针对级联抗毁性的研究主要集中在网络拓扑结构方面,还应考虑网络中的动力学因素,例如电力网、交通网、物流网等实际网络的节点或边都承载着负荷并且有一定的容量限制.节点或边故障将会导致负荷以一定规则在网络中分配,进而可能导致更多节点或边上的负荷超出其最大承载能力而过载,最终将导致网络部分功能异常甚至整个网络的崩溃[10-12],这种类型的级联故障被认为是负荷作用下的级联失效.
结合复杂网络理论进行作战网络的研究是一个全新的视角,是网络化作战研究的有力推手.之前有一些学者基于复杂网络理论对作战网络进行了相关研究.Dekker[13]研究了规则网络、WS网络、ER网络以及BA网络等模型与作战结果之间的关系;田旭光等[14]将指挥控制系统组成看作一种复杂网络结构,借鉴网络修复及重构机制,结合作战指挥原则,建立了自适应重构模型;张强等[15]为动态评估作战组织结构对作战效能的作用影响,采用复杂网络分析了信息化条件下作战组织结构的网络化特性.而这些模型以及算法往往忽略了“网络中心战”背景下,作战网络是一个动态的复杂的相依网络,各子网之间更是紧密联系、相互支持.因此,网络上非常小的一部分节点的失效甚至会造成系统中多个相依网络的完全崩溃,这在军事系统中会是灾难性的.
本文首先依据军事系统的实际交联关系选择C2网和传感器网构建非对称双层相依作战网络模型.其次,考虑网络中连边的失效及负荷传递,提出基于局部分配的非线性“负荷-容量”模型;最后仿真分析连边遭受蓄意攻击时,负荷及容量与网络级联抗毁性的关系,并与WS-WS双层对称网络模型进行对比.仿真结果验证了模型的合理性,并且为负荷作用下非对称相依作战网络的级联抗毁性研究提供有价值的参考.
1 非对称双层相依作战网络模型
作战网络之间的交互关系如图1所示,由传感器节点组成的传感器网,指挥控制节点组成的指挥控制(command and control,C2)网,以及由各类武器组成的火力打击网之间是相互沟通、互相依赖的.传感器网是一个四通八达、功能强大的信息网络,负责完成战场信息的集成;C2网是整个作战网络的中枢,对整体作战效能的发挥起着关键性作用.C2单元根据传感器单元提供的态势信息以及火力打击单元反馈的作战效果,动态地调整作战指令,保证各作战平台的同步进行,并动态分配任务;火力打击单元基于传感器网快速生成的高质量战场态势分析,以及指挥控制网提供的作战意图,最终实现对目标的实时精确打击,而打击后的效果又以情报信息的方式反馈回传感器网络[16].

图1 作战网络交互关系
依据上述指挥控制关系构建非对称双层相依作战网络模型,如图2所示,由具有层级加权结构的C2网(子网A)和单一层级结构的传感器网(子网B)构成.各子网内的节点连接关系称为内部边,子网间的连接表示两者之间的相互依赖关系,称为耦合边.两子网的节点数目相等,并且建立“一一对应”的随机连接关系.例如,子网A中的一个节点iA只随机与子网B中的一个节点jB耦合,节点耦合概率设为p1.
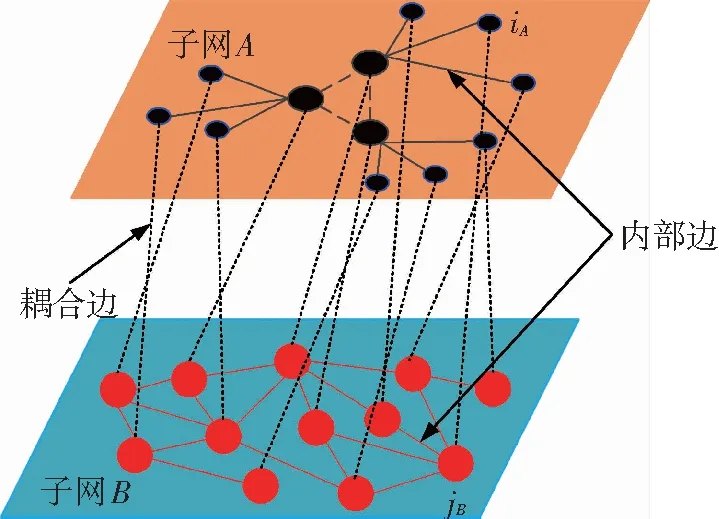
图2 非对称双层相依作战网络模型
Fig.2 Model of asymmetrical two-layered interdependent operational networks
该模型可由集合G(V,E,W)来描述,其中,V=VA∪VB表示网络中两个子网节点数之合;E=Einternal∪Ecoupling表示内部边和耦合边的集合;W为邻接矩阵,表示为

式中:矩阵元素wij为相邻两点间连接关系的权重,wij∈[0,).当节点不相连时,wij=0;子矩阵WA、WB分别为子网A和B的内部连接关系;WAB、WBA分别为两子网间的耦合连接关系.本文考虑无向网络,因此,邻接矩阵W是对称矩阵,每个子矩阵都是对称的,对于任一元素wij=wji.在此,定义节点强度si表示与网络中任意点i相连的所有连边权重之和,表示为
式中:Γi为节点i的邻居集合,包含同子网的邻居节点与相依子网中的邻居节点;si既考虑了节点的邻居节点数目,又考虑了与邻居节点之间连边的权重.
1.1 C2子网构建
C2子网(子网A)中各指挥层之间的不同权重和隶属关系,使得网络具有层级加权的特性.子网A中存在纵向的指挥信息流,而无横向的协同信息流,即除最高层节点之间存在连接之外,其余同层节点之间无连接.给定指挥控制层数L和指挥跨度M,就可以生成一个类似树状结构的网络.指挥跨度M是一个节点能够直接指挥的下级节点个数.算法步骤如下:首先,设定网络最高层次节点数量n1,层次号标志l=1,建立全连通网络,连边权重值设为w1.然后,按跨度M生成第2层,置层次号标志l=2,重复上一步骤,直至l=L,具有层级加权结构的C2子网生成.除第1层之外其余层内不存在连边,设置层间连边的权重值为
wl,l+1=w1-f(l)·(l-1),
式中f(l)为与层级l相关的函数,控制层间连边的权重值.同时考虑耦合边的权重等于所连接的子网A中节点连边权重的最大值.
1.2 传感器子网构建
传感器子网(子网B)按照WS小世界模型演化生成.小世界网络相比于其他网络而言,具有最短及最有效的路径[17],同等条件下可以提高网络信息流的传输.子网内节点处于同等地位,网络内连边的权重值相同.通过调节随机重连概率p2∈[0,1]实现从规则网络到ER网络的过渡.p2=0时生成最近邻耦合网络;p2=1时生成随机网络;当p2∈(0,1)生成的网络为不同调节比下的WS小世界网络模型.
2 级联失效模型
目前,针对级联抗毁性的研究绝大多数假设网络节点上承载负荷[18-20],而忽略在现实中连边通常也承载负荷,例如交通网中链路上的交通流等.本文的研究考虑连边负荷的存在,当连边受到攻击失效时,其负荷依据一定规则分配,不仅分配给内部边,同时也会分配给与之耦合的耦合边,进而可能造成某些连边负荷超过其容量而故障,引起新一轮的级联故障,直到网络中不再有新的连边失效.
早期Motter[21]提出了一种“全局定义,全局分配”的级联故障模型.以全局变量介数定义初始负荷Li,当节点因故障而被移除时,网络介数随机发生变化,可能导致部分节点负荷超出其容量而故障,节点的去除引起介数的进一步变化,并将引发新一轮的级联故障.节点i的容量Ci与其初始负荷Li呈线性关系,可表示为
式中β0为容量系数.基于全局变量进行分析的级联故障模型需要获取网络全部拓扑结构的实时信息,计算量大,对时间要求较高.Wang等[22]则提出了一种“局部定义,局部分配”的级联故障模型.采用基于局部变量度定义初始负荷Li,并且初始负荷首先分配给其邻居节点,再通过邻居节点传递到它的二阶邻居节点,二阶邻居节点负荷进一步传递给更高阶的邻居节点.
由于作战网络拓扑结构庞大且实时变化,本文借鉴“局部定义,局部分配”的思想,定义连边的初始负荷为与两端节点强度相关的函数,则节点i与节点j之间的连边的初始负荷Lij可表示为
Lij(0)=(si·sj)γ,
式中γ>0为可调参数,控制连边初始负荷的分布.当网络中的某个连边遭到摧毁或出现故障时,失效边的负荷将会传递给邻居连边.
而Kim等[23]对航空网、交通网、电力网等实际网络的分析发现,网络中容量较小的节点(边)反而具有较大的空闲容量,即大多数实际网络中,负荷和容量并非简单的线性关系.本文采用改进的非线性的“负荷-容量”模型,连边容量与初始负荷之间的关系,可以表示为
Cij=Lij(0)+βLij(0)θ,
式中β>0、θ>0分别为容量参数.该模型包含两个可变参数,灵活性更高.在初始负载较小时,拥有较大的额外容量,而在初始负荷较大时,容量C趋向于负载,额外容量逐渐减小,更符合实际网络的情形,如图3所示.当θ=1时退化为文献[21]提出的线性“负荷-容量”模型.
图4展示了连边失效后所引发的局部负荷重分配过程.其中实直线表示内部边,虚直线表示耦合边.当子网A中的内部边eiAhA失效时,其上的负荷分配给两端点的邻居连边,包括内部边和耦合边,用弧形箭头表示.
当邻居连边自身的负荷加上分配给它的负荷超出了自身的容量时,例如,内部边eiAkA和耦合边eiBkB的负荷超过其容量导致失效,并引发新一轮的负荷重分配.依据局域分配原则,当耦合边eiAjB失效后,其负荷分配给iA在网络A中的邻居边iAjA的比例为
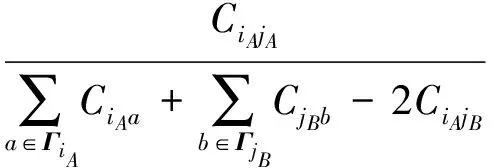
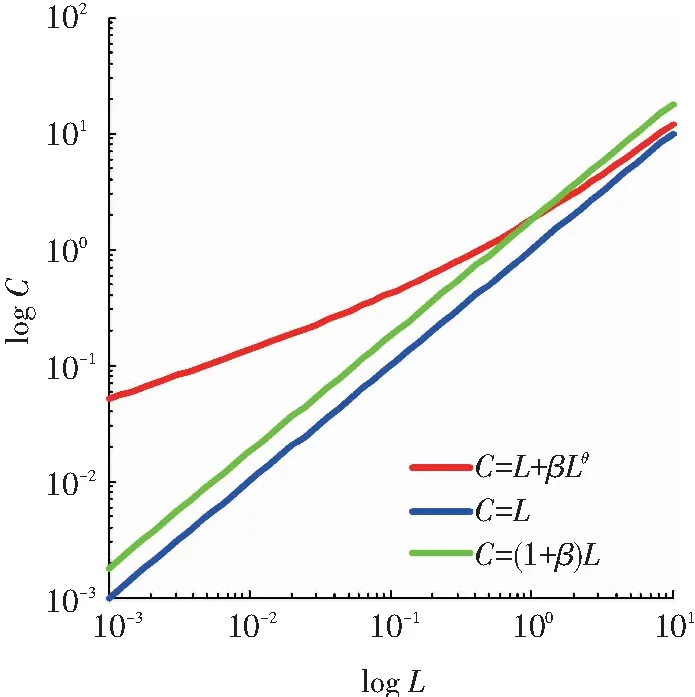
图3 “负荷-容量”模型关系
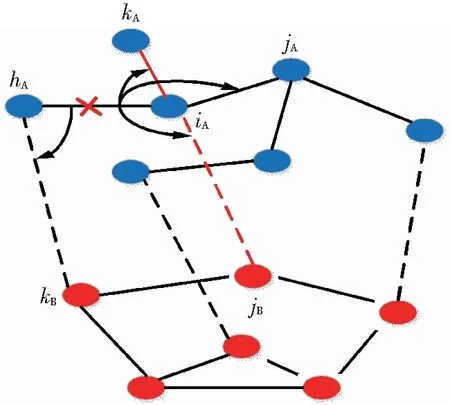
图4 局部负荷重分配示意
分配给节点jB在网络B中的邻居边jBkB的比例为
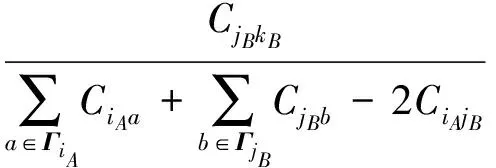
式中:ΓiA、ΓjB分别为节点iA(jB)的邻居集合;LiAjB为连边eiAjB的初始负荷;ΔLiA→jA为分配给连边eiAjA的负荷;ΔLjB→kB为分配给连边ejBkB的负荷.当对于任意边存在Cmn>Lmn+ΔLm→n时,网络中的级联故障才终止.同时,定义连边失效对应的网络抗毁性的指标为
式中:Eij为级联故障后网络中的连边总数;E为级联故障前网络的连边总数.显然,R越大,网络的抗毁性越好.
模型的计算步骤及复杂度分析如下.
1)初始化3个邻接矩阵:传感器子网邻接矩阵WA、C2子网邻接矩阵WB、耦合连接子邻接矩阵矩阵WAB(WBA);计算复杂度均为O(VA)或者O(VB).其中,VA=VB.
2)计算耦合网络中每个节点的节点强度Si,并计算连边的初始负荷L和容量C;计算复杂度分别为O(VA2)和O(E).
3)攻击子网A中初始负荷最大的边,将其归入失效连边集合E′;计算复杂度为O(E).
4)依据连边负荷局部重分配原则将失效边的负荷重新分配给相邻的所有连边,将失效边删除,同时置集合E′为∅.
5)遍历审核每条邻居连边的负荷,当负荷超过容量时,删除该连边,将其归入失效连边集合E′.判断集合E′是否为∅,当E′≠∅时,继续执行步骤4).当E′=∅时,级联失效终止,计算步骤结束.步骤4)、5)的计算复杂度最大为O(VAE).
综上所述,级联失效过程的计算复杂度为:O(VA2+VAE).
3 结果及分析
初始参数设置为:子网节点数目VA=VB=340,耦合连接概率p1=0.7,耦合边的权重与所连接的子网A中节点连边的最大权重值一致.子网A中最高层节点数n1=4、层次数L=4、跨度M=4,则下属各层节点数分别为16、64、256;设f(l)=C0=2为常数,最高层内部边权值为10,层间权值分别为8、6、4.子网B中随机重连概率p2=0.1.
攻击策略为蓄意攻击C2网中初始负荷最大的连边.如果某些连边恰巧具有相同的负荷,将从中随机选择.子网A中的故障会引发相依子网B中的故障,反过来子网B中的故障又会传递给子网A,此过程不断迭代直至不再有新的故障产生.所有仿真结果均为1 000次蓄意攻击后的统计平均值.
图5显示的固定负荷参数γ=0.8时,分析网络容量与级联抗毁性之间的关系,并且将子网A为孤立状态时的抗毁性与相依状态时的抗毁性进行对比分析.仿真结果表明,无论是在孤立网络状态还是相依网络状态下,随着容量参数β和θ的增大,抗毁性指标R的曲线不断上升,表明连边容量越大,网络的级联抗毁性更好.
图6显示的固定容量参数θ=0.8,分析连边初始负荷与级联抗毁性之间的关系,并且将子网A孤立状态时的抗毁性与相依状态时进行对比分析.值得注意的是,负荷参数γ越大,R曲线越靠下,即子网A的级联抗毁性与负荷呈负相关关系.同样验证了子网A的级联抗毁性与容量参数β呈正相关.
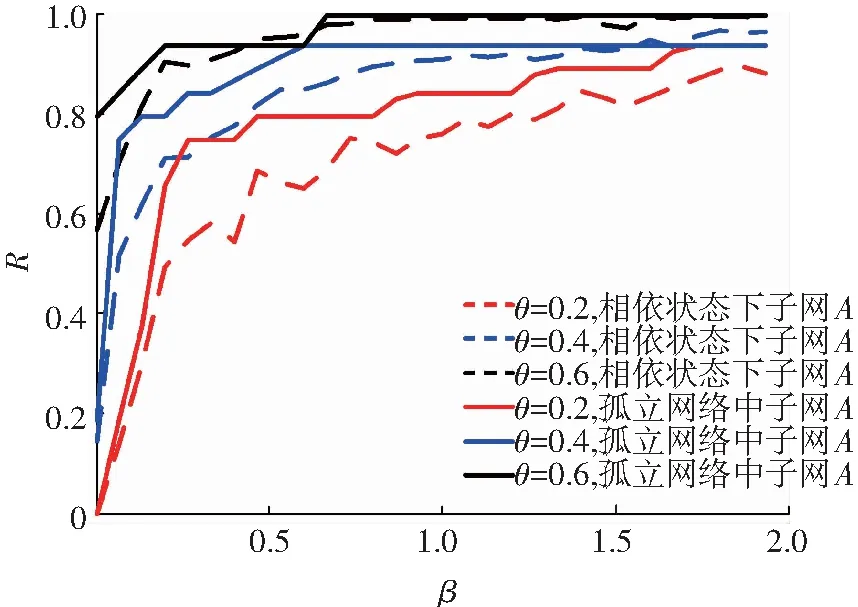
图5 级联抗毁性与容量之间的关系(γ=0.8)
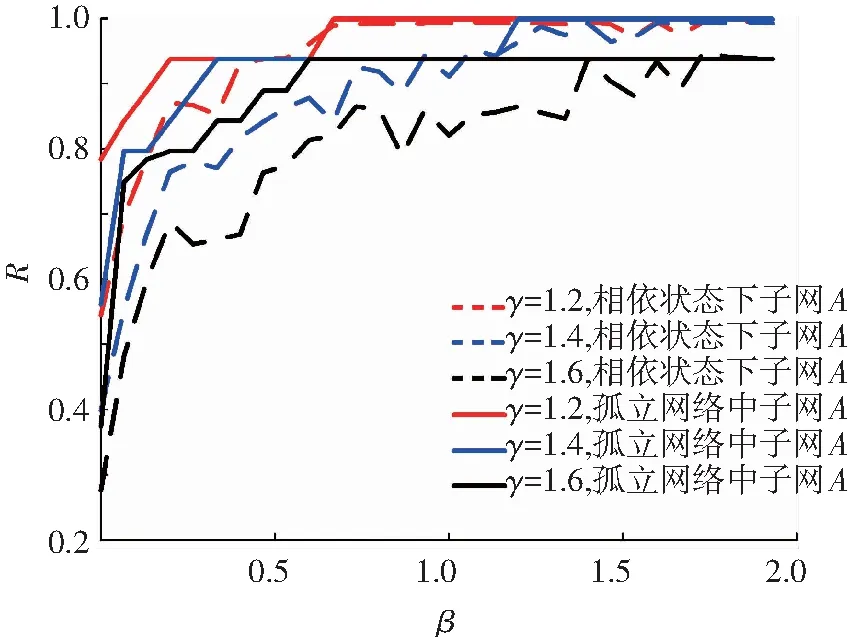
图6 级联抗毁性与初始负荷之间的关系(θ=0.8)
分析图5、6发现,同等参数状况下,相依状态下子网A的级联抗毁性曲线比孤立网络状态时的R小,且变化更缓慢.说明相依关系使得网络的级联抗毁性变差,同时使得级联失效过程变缓慢.除此之前,观察曲线R中的平台现象,分析其原因是子网A的层级权重结构导致的.因为连接相同层级邻居节点的连边占大多数,导致往往具有相同的初始负荷和容量,被分配新负荷的比例几乎相等,失效概率也几乎相等.而那些连接非同层节点的连边只是少数,具有不同的失效概率.当大部分连边失效时就导致了R曲线的急剧变化,而随着连边容量的增加,仅存在极少数连边的失效,导致R曲线出现一个平台期.
图7显示的是选取两组不同的参数γ=0.8,θ=0.6和γ=0.6,θ=0.8时,对称相依网络WS-WS与非对称相依作战网络的子网级联抗毁性的对比.WS-WS相依网络中参数的配置与非对称相依网络中子网B的参数配置相同.图7(a)、(b)显示,在对称相依网络中,两子网的级联失效曲线几乎一致,而在非对称相依网络中,子网A和B的级联失效曲线出现了分离.非对称相依网络的级联抗毁性要比对称相依网络的级联抗毁性差.层级加权结构的子网A的级联抗毁性比子网B要差.
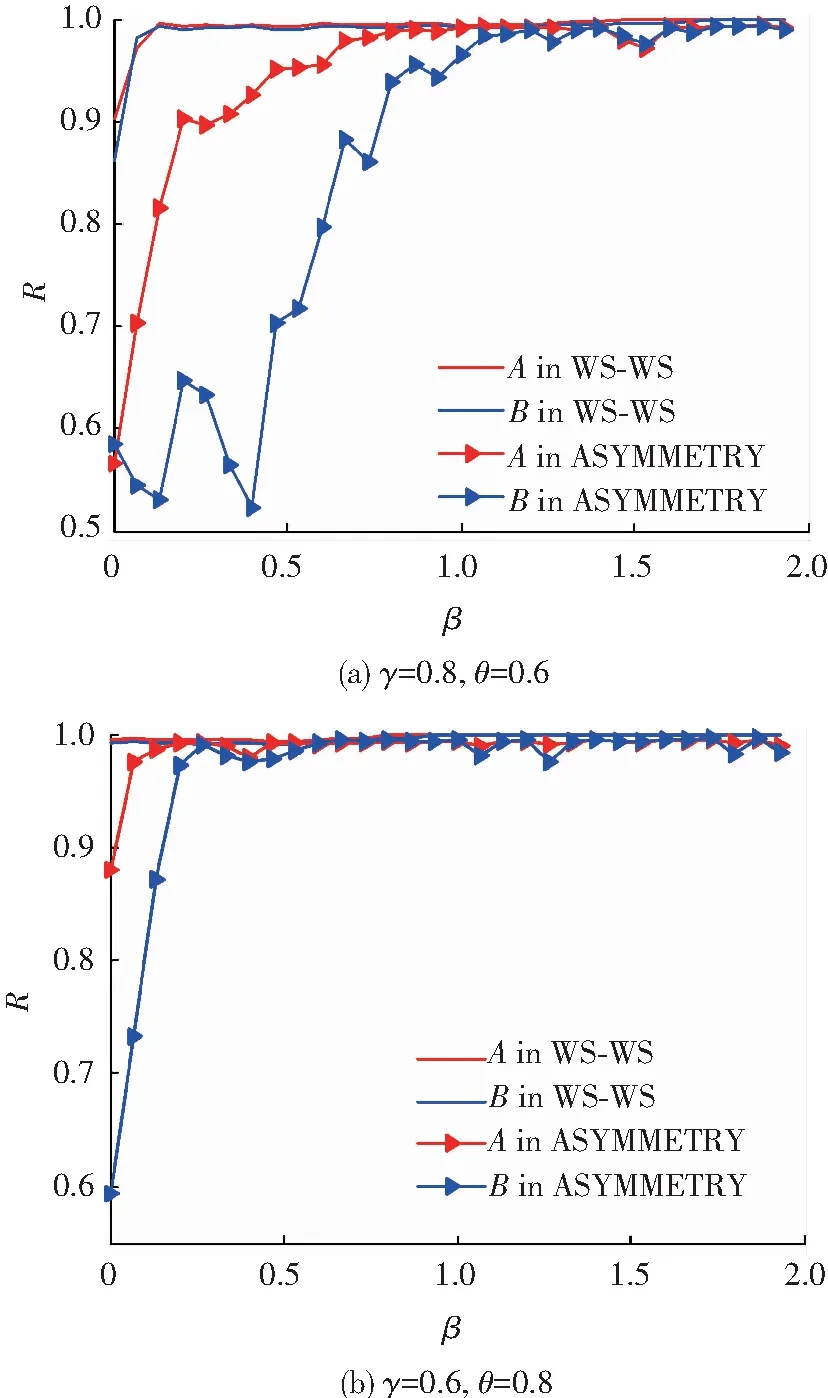
图7对称相依网络与非对称相依网络的级联抗毁性对比
Fig.7 Comparison between symmetrical and asymmetrical interdependent networks
4 结 论
1)无论是孤立状态还是相依状态下,相依网络的级联抗毁性与连边容量变化呈正相关,而与负荷的变化呈负相关.
2)相依网络的级联抗毁性比孤立网络要差,并且相依网络级联失效的过程更缓慢.孤立C2网络中的层级加权结构使得级联故障中出现短暂的平台期.
3)与对称WS-WS相依网络相比.非对称作战网络的级联抗毁性更差.在非对称相依网络中,子网之间的级联抗毁性不同,而相依对称网络中子网的级联抗毁性几乎相同.
[1] WATTS D J, STROGATZ S H. Collective dynamics of “small-world” networks[J]. Nature, 1998, 393(6684):440-442.DOI:10.1038/30918.
[3] 周涛, 张子柯, 陈关荣, 等. 复杂网络研究的机遇与挑战[J]. 电子科技大学学报, 2014, 43(1):1-5. DOI:10.3969/j.issn.1001-0548. 2014.01.001.
ZHOU Tao, ZHANG Zike, CHEN Guanrong, et al. The opportunities and challenges of complex networks research[J]. Journal of University of Electronic Science and Technology of China, 2014, 43(1):1-5. DOI:10.3969/j.issn.1001-0548.2014.01.001.
[4] 王甲生,吴晓平,陈永强. 不同信息条件下加权复杂网络抗毁性仿真研究[J]. 中南大学学报(自然科学版), 2013,44(5):1888-1894.
WANG Jiasheng, WU Xiaoping, CHEN Yongqiang. Invulnera-bility simulation of weighted complex networks with different information[J].Journal of Central South University (Science and Technology), 2013,44(5):1888-1894.
[5] BULDYREV S V,SHERE N W, CWILICH G A. Interdependent networks with identical degrees of mutually dependent nodes[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics,2011,83(1):016112. DOI:10.1103/PhysRevE.83.016112.
[6] 彭兴钊, 姚宏, 肖明清,等. 加权网络的级联故障建模及其抗毁性分析[J]. 系统工程与电子技术, 2014,36(6):1096-1102. DOI: 10.3969/j.issn.1001-506X.2014.06.13.
PENG Xingzhao, YAO Hong, XIAO Mingqing, et al. Cascading failure model for weighted networks and invulnerability analyses[J]. Systems Engineering and Electronics, 2014, 36(6): 1096-1102. DOI:10.3969/j.issn.1001-506X.2014.06.13.
[7] BULDYREV S V, PARSHANI R, PAUL G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7291): 1025-1028. DOI: 10.1038/nature08932.
[8] GAO Jianxi, BULDYREV S V, STANLEY H E, et al. Networks formed from interdependent networks[J]. Nature Physics, 2012, 8(1):40-48. DOI: 10.1038/NPHYS2180.
[9] 陈世明, 邹小群,吕辉,等.面向级联失效的相依网络鲁棒性研究[J]. 物理学报, 2014,63(2):028902(1-10). DOI:10.7498/aps.63.028902.
CHEN Shiming, ZOU Xiaoqun, LÜ Hui, et al. Research on robustness of interdependent network for suppressing cascading failure[J]. Acta Physica Sinica, 2014,63(2):028902(1-10). DOI:10.7498/aps.63.028902.
[10]WANG Jianwei, JIANG Chen, QIAN Jianfei. Robustness of interdependent networks with different link patterns against cascading failures[J]. Physica A, 2014,393:535-541. DOI:10.10 16/j.physa.2013.08.031.
[11]TAN Fei, XIA Yongxiang. The robust-yet-fragile nature of interdependent networks[J]. Physical Review E, 2015,91(5):052809. DOI:10.1103/PhysRevE.91.052809.
[12]韩海艳, 杨任农, 李浩亮, 等. 双层相依指挥控制网络级联失效研究[J]. 中南大学学报(自然科学版), 2015, 46(12): 4542-4547. DOI: 10.11817/j.issn.1672-7207.2015.12.022.
HAN Haiyan, YANG Rennong, LI Haoliang, et al. Cascading failure on two-layered interdependent command and control network[J]. Journal of Central South University (Science and Technology), 2015, 46(12): 4542-4547. DOI:10.11817/j.issn.1672-7207. 2015.12.022.
[13]DEKKER A H. Network topology and military performance[C]//Proceedings of the International Congress on Modeling and Simulation. Australia: [s.l.], 2005: 2174-2180.
[14]田旭光,朱元昌,罗坤,等. 基于复杂网络理论的指挥控制系统自适应重构模型[J]. 系统工程与电子技术, 2013, 35(1): 91-96. DOI: 10.3969/j.issn.1001-506X.2013.01.15.
TIAN Xuguang, ZHU Yuanchang, LUO Kun, et al. Adaptive reconstruction model for command and control and control system under information age based on complex network theory[J]. Systems Engineering and Electronics, 2013, 35(1): 91-96. DOI:10.3969/j.issn.1001-506X.2013.01.15.
[15]张强,李建华,沈迪,等. 复杂网络理论的作战网络动态演化模型[J].哈尔滨工业大学学报, 2015, 47(10):122-128. DOI: 10.11918/j.issn.0367-6234.2015.10.023
ZHANG Qiang, LI Jianhua, SHEN Di, et al. Dynamic evolution model of operational network based on complex network theory[J].Journal of Harbin Institute of Technology, 2015, 47(10): 122-128. DOI:10.11918/j.issn.0367-6234.2015.10. 023.
[16]金伟新,肖田元.作战体系复杂网络研究[J]. 复杂系统与复杂性科学, 2009,6(4):12-25.
JIN Weixin, XIAO Tianyuan. Research on the combat SoS complex network[J]. Complex System and Complex Science, 2009, 6(4): 12-25.
[17]LÜ Linyuan, CHEN Duanbing, ZHOU Tao, et al. The small world yields the most effective information spreading[J]. New Journal of Physics, 2011, 13(12):123005(1-10). DOI:10.1088/1367-2630/13/12/123005.
[18]BRUMMITT C D, D’SOUZA R M, LEICHT E A, et al. Suppressing cascades of load in interdependent networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109(12): E680-E689. DOI: 10.1073/pnas.1110586109.
[19]QIU Yuzhuo. Optimal weighting scheme and the role of coupling strength against load failures in degree-based weighted interdependent networks[J]. Physica A: Statistical Mechanics and its Applications, 2013, 392(8): 1920-1924.DOI:10.1016/j.physa.2013.01.014.
[20]GOH K I, KAHNG B, KIM D, et al. Universal behavior of load distribution in scale-free networks[J]. Physical Review Letters, 2001, 87: 278701. DOI:10.1103/PhysRevLett.87.278701.
[21]MOTTER A E. Cascade control and defense in complex network[J].Physical Review Letter, 2004, 93(9): 098701. DOI: 10.1103/PhysRevLett.93.098701.
[22]WANG Wenxu, CHEN Guanrong. Universal robustness characteristic of weighted networks against cascading failure[J]. Physical Review E, 2008,77:026101.DOI:10.1103/ PhysRevE. 77.026101.
[23]KIM D H, MOTTER A E. Resource allocation pattern in infrastructure networks[J]. Journal of Physics A: Mathematical and Theoretical, 2008, 41(22): 224019. DOI: 10.1088/1751-8113/ 41/22/224019.
Cascadingfailuremodelofasymmetricalinterdependentoperationalnetworksunderedgeattack
HAN Haiyan1, YANG Rennong1, WANG Zhe1, SONG Xiaoou2
(1.School of Aeronautics and Astronautics Engineering, Air Force Engineering University, Xi’an 710038, China;2.Information Engineering Department, Armed Police Force Engineering University, Xi’an 710086, China)
The complex network theory provides a new perspective in the study of operational network, a powerful method to investigate the relationship between network structure and function. To study the load-induced cascading failure of interdependent operational networks, two-layered asymmetrical interdependent network is constructed according to the interactive relationship of military system. Then, an improved “load-capacity” model based on local load redistribution is proposed to study the edge failure and load transfer, and the computation complexity of the cascading model. Thirdly, the influence of edge load and capacity on the cascading invulnerability is simulated under malicious edge attacks and compared with a WS-WS symmetrical interdependent network. The results show that the robustness against malicious attacks is positively related to the capacity, yet negatively to the load either in isolated or interdependent state. A short plateau appears in the progress of cascading due to the hierarchical weighted structure of C2 subnet under isolated status. The cascading invulnerability of asymmetrical interdependent operational networks is worse than the symmetrical one. The two subnets in the former network have different invulnerability performances, while the subnets in the latter system almost have the same performance.
asymmetrical interdependent operational networks; “load-capacity” model; malicious edge attack; load redistribution; cascading invulnerability
10.11918/j.issn.0367-6234.201604029
TP391;N945.1
A
0367-6234(2017)10-0120-06
2016-04-07
陕西省科学技术研究发展项目(2013kjxx-82)
韩海艳(1988—),女,博士研究生;
杨任农(1969—),男,教授,博士生导师
杨任农,yangrn6907@foxmail.com
(编辑张 红)
—— “T”级联

