超高速弹丸膛口流场结构分析
李子杰,王 浩,陈健伟
(南京理工大学 能源与动力工程学院,南京 210094)
超高速弹丸膛口流场结构分析
李子杰,王 浩,陈健伟
(南京理工大学 能源与动力工程学院,南京 210094)
为了计算和分析超高速弹丸膛口流场的分布状况,建立了超高速弹丸从膛底飞离出炮口整个过程的膛口流场二维轴对称数值仿真模型.基于有限体积法,采用分块网格划分的整体运动处理方法,结合结构动网格技术及Realizablek-ε湍流模型,耦合内弹道及后效期过程,利用六自由度运动方程控制弹丸运动,以300 mm平衡炮为例,研究了1 730 m/s发射速度下的超高速膛口流场特性.计算结果表明:超高速运动的弹丸在距膛口3.3 m远处便形成了清晰的初始流场,弹前激波到达炮口处压力达到了3.8 MPa左右.喷射出的火药燃气速度达到2 500 m/s,但火药燃气仍未能追赶并包围弹丸,因此膛口流场对超高速弹丸运动的影响不同于对中低速弹丸运动的影响;膛口形成了由冠状冲击波、弹底激波、反射激波、马赫盘构成的多层次激波、间断面相互叠加的完整波系,该发射条件下的膛口流场异常强烈,波系结构更加明显.
超高速;膛口流场;动网格;二维轴对称;特性分析
膛口流场是非定常、带有强激波间断的复杂流场.在膛内火药燃气推动作用下,加速运动的弹丸不断压缩弹前空气,形成弹前冲击波和初始流场[1-2].在火炮射击的后效期,高温高压燃气迅速释放,进入初始流场,膛口周围出现各种复杂的物理和化学现象,弹丸在火药燃气推力作用下继续加速,膛口附近形成了复杂的瞬态膛口流场波系结构,并在远场产生冲击波和噪声[3-4].大口径高超速平衡炮炮膛口流场的有害扰动是极其强烈的,而且对弹丸的稳定飞行影响较大,但通过试验直接测量膛口流场的特性参数非常困难,因此,通过数值模拟分析大口径高超速平衡炮的膛口流场特性,是一个经济有效的方法[5].
目前,国内外已经对膛口流场进行了相关的试验和研究[6-8].Jiang等[9]用基于ALE方程及动网格技术对44 mm口径弹丸由膛内到膛外直到飞离初始流场的整个过程进行数值模拟.江坤等[10]利用结构网格对122 mm车载火炮的膛口流场进行数值模拟,对初速为713 m/s的弹丸发射过程中的流动现象进行了分析,得到了较为可信的结果.代淑兰等[11]采用三维非定常化学反应流控制方程组对带制退器的7.62 mm口径、735 m/s初速的弹丸膛口燃烧流场进行了数值模拟,清晰的描述了膛口流场的发展过程结构和性质及弹丸与流场的相互影响.Love[12]通过实验和理论方法对轴对称自由射流进行了研究,分析了射流马赫数、喷管形状等因素对轴线上的膛口气流参数分布的影响.高树滋等[13]采用MUSCL差分格式对膛口流场进行了分析,得到了由空气冲击波和射流近场结构所组成的全流场流动图像.乐贵高等[14]利用Osher 格式及非结构网格对二、三维可压缩欧拉流动方程组对某型号火炮膛口气流现象进行分析和计算.
上述所做的研究均基于155 mm口径以下的火炮,多以常规初速或低速发射弹丸为研究对象.由于弹丸初速相对较低,多以膛口附近处开始计算,并将膛口压力或弹丸速度简化为定值.而对于300 mm大口径超高速弹丸的初始流场及火药燃气流场的射流结构的分析未见报道.本文建立该发射条件下膛口流场的二维轴对称数值仿真模型,耦合内弹道过程,研究超高速弹丸自膛底飞出膛口时的初始流场和火药燃气流场的射流结构,并对结果进行了分析,为大口径高超速火炮的设计与试验提供理论指导,为深入研究奠定良好基础.
1 数学模型
1.1 控制方程
当不考虑外加热和彻体力的影响时,笛卡尔坐标系下的二维轴对称可压缩非定常的N-S方程组为[15]

式中:Q为守恒变矢量;F、G分别为坐标方向的通量;S为轴对称源项,具体表达式为:
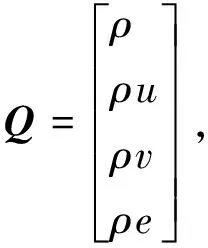
其中应力项为:
压力由理想气体方程给出,即
式中:ρ为气体密度;u、v分别为x、y方向的速度分量;e为总能量;γ为气体比热比;μ为层流黏性系数;τθθ、τxx、τyx、τyy分别为不同方向的黏性力;k为热导率;qx、qy分别为单位质量的体积加热率;系数σ决定流动的类型,当σ=1时,为二维轴对称流动模型,当σ=0时,为二维平面流动模型.
1.2 湍流模型
本文所利用的湍流模型为Realizablek-ε模型.该模型比起标准k-ε模型有两个主要的不同点:1)Realizablek-ε模型为湍流黏性增加了一个公式;2)为耗散率增加了新的传输方程.
引入Boussinesq的线性涡黏假设,雷诺应力表达式为
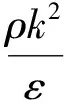
2 动网格与边界条件
2.1 动网格方法
为了处理计算过程中由于弹丸运动所引起的网格变化,需要采用动网格技术.动网格算法主要用来计算内部网格节点的调节,有3种算法:铺层法、弹性光顺法和局部重构法.由于本文中考虑到弹丸只沿一个方向做平移运动,所以采用铺层法即可实现对弹丸运动的模拟.铺层法中需要对网格的分割因子和合并因子进行设定.由于弹丸的运动,使得弹后网格随弹丸沿x轴向前平移,靠近膛底的一层网格被拉长,网格边长为hs,网格超出计算域边界部分被截断,靠近计算域边界的一层网格长度为hc,假设给定的理想网格尺寸为hi,当新生成的网格尺寸满足h≥(1+cs)hi时,网格被分割成两个,当网格尺寸满足h≥cchi时,网格将合并为一个网格.本算例中取hi=5 mm,cs=0.4,ci=0.1.
2.2 网格划分与边界条件
对复杂流场进行模拟时,很多情况下很难生成单块高质量结构网格,此时可以采用分区拼接网格的方法进行处理.将整个计算域分为3个区域:弹后Ⅰ区、弹前Ⅱ区、膛口周围流场Ⅲ区,炮管总长29.6 m,管壁厚度为50 mm,如图1(a)所示.初始时,弹丸距膛底100 mm,膛口周围流场区域长13 m,宽3 m.最小网格尺寸为2 mm,为避免非结构网格带来过多的计算量与格式耗散,本文均采用结构化网格进行划分,共28万个网格.为验证本文所采用的网格划分方法及网格尺寸合理,以总网格数35万模型作为对比,两种情况下弹底压力最大误差不超过1%,证明结论与网格划分无关.
图1(b)给出了镜像后的初始网格划分模型.计算域中,设定身管、膛口为固壁边界条件,弹丸为移动固壁边界,弹丸在膛内运动阶段由内弹道UDF程序控制,出膛口后由六自由度UDF程序控制其运动,膛底设为压力入口边界条件,计算域边界为压力出口边界条件.壁面均假定为绝热,壁面上温度为临近壁面网格点温度.

图1 超高速弹丸膛口流场物理模型示意
Fig.1 Physical model of the hyper-velocity projectile muzzle flow field
2.3 计算模型
本文模型中,弹丸质量为160 kg,平衡体重2 000 kg,总装药量为240 kg,图2(a)、(b)分别给出了此平衡炮内弹道过程的弹底压力随时间的变化曲线和速度随时间的变化曲线.由计算结果得出,弹丸出膛口速度为1 730.4 m/s,膛口压力为46.34 MPa,运动时间为37.6 ms[16-17].弹丸后效期的膛口压力随时间呈指数分布[18-19],其压力分布如图2(c)所示.身管外流场区域始压力为101 325 Pa,初始温度为300 K.

图2 内弹道及后效期计算参数分布曲线
3 结果与分析
3.1 数值验证
本文主要对300 mm大口径超高速平衡炮的发射过程进行了数值模拟,采用分块网格划分的整体运动处理方法及Realizablek-ε湍流模型,耦合内弹道过程及六自由度程序控制弹丸运动.为了验证本文算法的可靠性,模拟以往研究采用分层动网格技术结合Roe的迎风格式得到的某48 mm口径530.0 m/s枪炮的膛口流场特性[20],并得到了一致的结果,图3、4给出了膛口流场压力等值线图与速度矢量图的对比,证明了本文算法的正确性.
3.2 初始流场分析
根据耦合内弹道过程的膛口流场数值计算,得到了大口径超高速平衡炮初始流场结构分布.弹丸在膛内推动弹前的空气柱,形成一系列压缩波,压缩波不断向膛口方向传播,由于后一个压缩波的传播速度总比前一个大,这些压缩波相互叠加形成了激波,激波在膛内逐渐加强,随着弹丸的加速运动,弹前空气被挤出膛口形成初始流场.典型的膛口流场的波系结构如图5所示.

图3 数值验证压力等值线图对比

图4 数值验证速度矢量对比
Fig.4 Comparison of velocity wectors for numerical verification
图6(a)~(h)显示了超高速弹丸初始流场的形成过程.当弹丸运动至34.3 ms时,初始流场即将形成,此时弹丸距膛口5.5 m,弹丸速度为1 658.3 m/s.初始冲击波的强度主要由弹丸初速的大小决定,弹丸初速越高,弹前激波及初始冲击波就越强.当弹丸初速在1 000 m/s左右时,弹前激波到达膛口时的气体压力一般为1~2 MPa,而由图6(a)可以看出,当弹丸以1 730 m/s超高速运动时,此压力达到了3.8 MPa左右,高于中小口径中低速发射条件下的1倍.压缩波在膛内形成轴对称涡流环,并随气流一起做轴向运动.由于波后的压力比外界压力高的多,于是形成了膨胀不足的初始流场.随着弹丸继续向前运动,初始流场逐渐形成并发展.
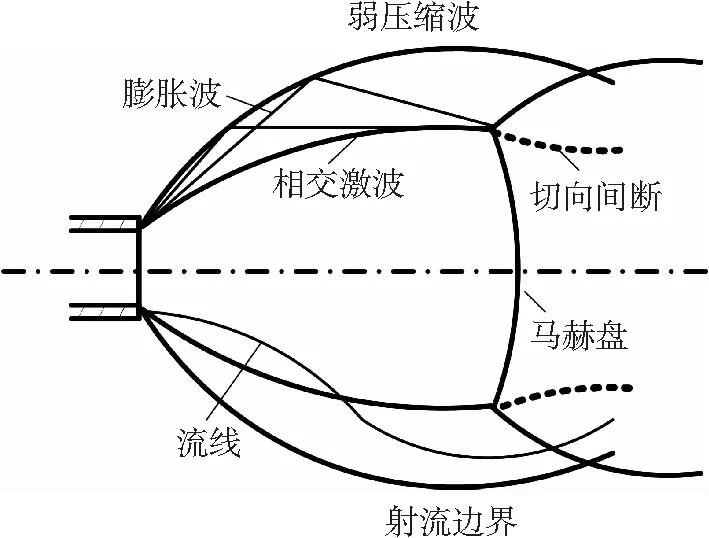
图5 膛口流场波系结构
当弹前空气被压缩流出膛口后,气体迅速膨胀,速度增大,压力降低,并向周围传播,在身管固壁处形成涡流,涡流所在位置出现负压.由图6(d)所示,在弹丸距膛口3.3 m处,已形成了清晰的初始流场.图6(f)可以较清楚的观察到初始冲击波、初始瓶状激波、马赫盘以及三波点.膛口附近的涡流也不断变大并向侧前方运动.由图6(g)可以看出,弹丸的圆柱部已运动出膛口,使膛内的弹前气体全部压出,气体不断膨胀向四周传播.被压缩的空气向前传播使得后方压力降低,周围空气流向该区域,并使弹丸周围涡流继续向前运动.
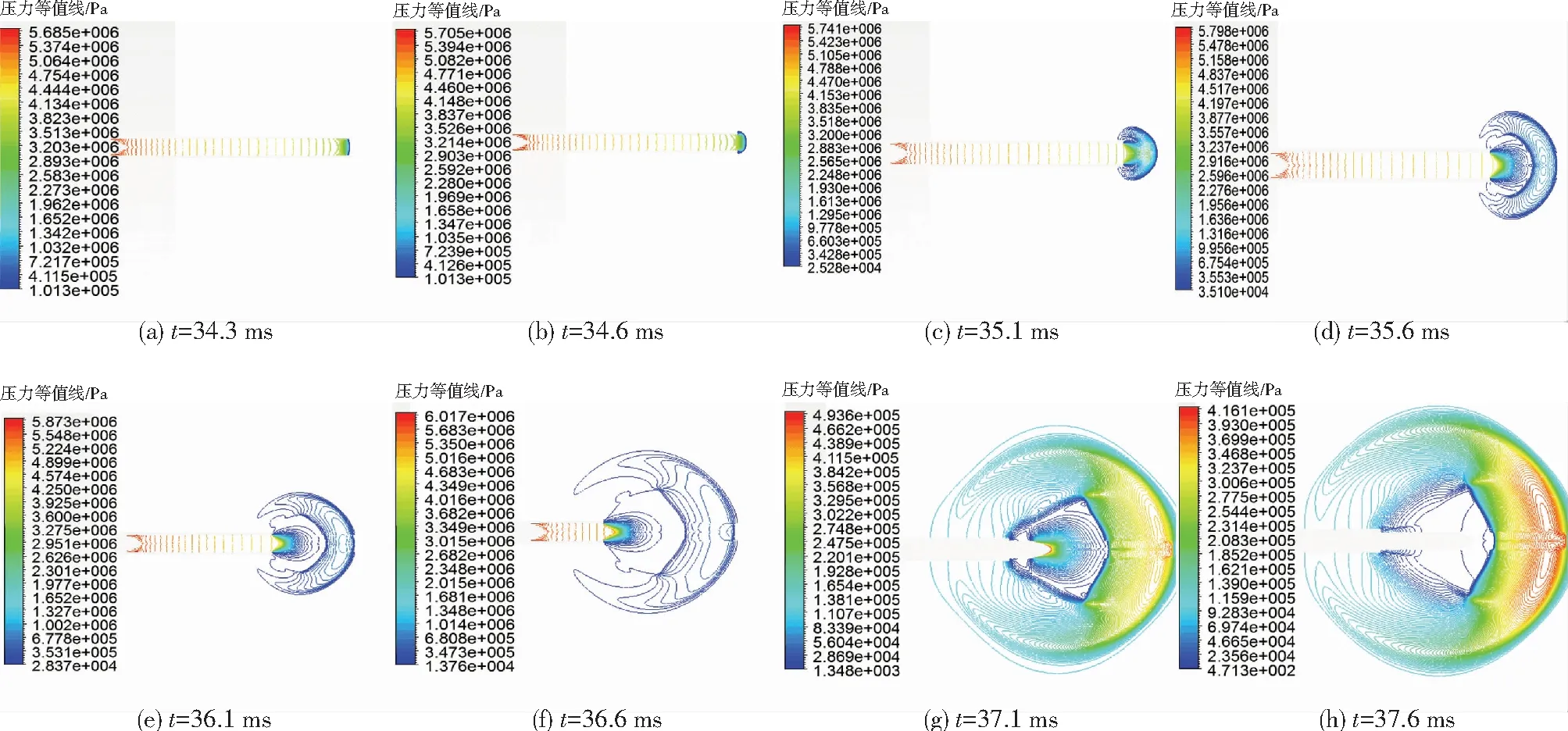
图6 超高速弹丸初始流场压力等值线
3.3 火药气体流场分析
随着弹丸运动出膛口,耦合后效期过程及弹丸六自由度运动方程,得到了火药燃气流场的分布状态.图7(a)~(g)给出了膛口流场的波系结构及其形成过程.由图7(a)所示,大口径超高速弹丸膛口冲击波异常强烈,高温高压火药气体首先从弹尾周围逸出,向侧前方迅速发展传播,速度高达2 500 m/s以上,而中小口径中低速发射状态火药燃气速度仅为1 500~1 800 m/s.由火药气体的速度矢量图(图8)可以清晰的看到火药气体的运动方向.气体推动膛口周围已被初始流场扰动过的空气,形成了膛口冲击波,由图7(b)可以看到清晰的膛口冲击波的形成.
图7 超高速弹丸流场压力等值线
火药气体向前运动追赶弹丸,由于弹丸初速高,2 500 m/s速度的火药气体不能包围弹丸.而对于中小口径中低速弹丸,由于弹丸弹身短、口径小、初速低,从膛口喷出的高温高压气体相对于弹丸初速高出几倍,很快将弹丸包围.图7(c)、(d)可以看到随着弹丸的运动逐渐摆脱了火药气体对其的包围.图7(d)可以清晰的看到弹底激波的形成,这是因为喷射出的火药气体射流大于弹丸的速度.由于初始流场主漩涡的作用,膛口冲击波波阵面在主漩涡环的中心处出现褶皱,弹底激波在膛口冲击波的作用下进一步加强并阻碍马赫盘的生长,随着弹底激波的作用越来越弱,马赫盘逐渐增大,瓶状激波不断扩大,膛口冲击波不断向远处传播并衰减.但膛口冲击波在不同方向上的衰减规律不同,膛口冲击波前方的强度要大于侧后方的强度.由图7(e)所示,弹丸侧面形成了起始于弹丸头部并脱离弹丸侧面向外延伸的剪切层,随着火药燃气持续喷出空气接触发生复杂的变化,射流的结构更加明显.
图7(f)可以清晰的看到膛口冲击波的三波点,膛口形成了由冠状冲击波、弹底激波、反射激波、马赫盘构成的多层次激波、间断面相互叠加的完整波系.图9(a)、(b)给出了弹丸出膛口后弹底压力及Ma随时间的变化情况,由图9可以看出,在1.0 ms以后火药燃气作用在弹底的压力基本为零,弹丸Mamax可以达到4.0以上.

图8 火药气体速度矢量

图9 弹丸压力与Ma随时间变化曲线
4 结 论
1)超高速运动的弹丸在膛内距膛口5.5 m处初始流场开始形成,距膛口3.3 m处已形成了清晰的初始流场,且冲击波到达膛口时压力高于中小口径中低速发射状态下1倍.
2)火药燃气流场异常强烈,火药燃气速度达到2 500 m/s以上,其波系结构更加明显,膛口射流结构更加剧烈.
3)弹丸以1 730 m/s初速运动时弹后气体不能追赶并包围弹丸,故对弹丸运动的影响不同于中小口径中低速发射状态.
[1] 王柏秋, 王聪, 魏英杰, 等. 超空泡射弹阻力系数数值模拟[J]. 哈尔滨工业大学学报, 2013, 45(3): 22-27.
WANG Baiqiu, WANG Cong, WEI Yingjie, et al. Drag coefficients of supercavitating projectile based on dynamic mesh[J]. Journal of Harbin Institute of Technology, 2013, 45(3): 22-27.
[2] GUHA A, SENGUPTA S. The fluid dynamics of the rotating flow in a Tesla disc turbine[J]. European Journal of Mechanics B/Fluids, 2013, 37: 112-123. DOI: 10.1016/j.euromechflu.2012.08.001.
[3] 张辉, 谭俊杰, 崔东明. 带膛口装置的流场数值模拟[J].火炮发射与控制学报, 2007, 2: 48-51. DOI: 10.3969/j.issn.1673-6524.2007.02.013.
ZHANG Hui, TAN Junjie, CUI Dongming. Numerical simulation method of flow field with muzzle attachments [J]. Journal of Gun Launch & Control, 2007, 2: 48-51. DOI: 10.3969/j.issn.1673-6524.2007.02.013.
[4] JONES A R, MEDINA A, SPOONER H, et al. Characterizing a burst leading-edge vortex on a rotating flat plate wing[J]. Experiments in Fluids, 2016, 57:52. DOI: 10.1007/s00348-016-2143-7.
[5]孙得川, 蔡体敏. 超声速流动中横向射流流场的影响参数[J]. 推进技术, 2001, 22(2): 147-150. DOI: 10.3321/j.issn:1001-4055.2001.02.017.
SUN Dechuan, CAI Timin. Effecting parameters of supersonic flowfield with secondary injection[J]. Journal of Propulsion Technology, 2001, 22(2): 147-150.DOI: 10.3321/j.issn:1001-4055.2001.02.017.
[6] MEGHDADI-ISFAHANI A H, TASDIGHI I, KARIMIPOUR A, et al. A joint lattice Boltzmann and molecular dynamics investigation for thermohydraulical simulation of nano flows through porous media[J]. European Journal of Mechanics-B/Fluids, 2016, 55: 15-23. 10.1016/j.euromechflu.2015.08.002.
[7] 何枫, 谢峻石, 郝鹏飞,等. 应用S-A模型的自由射流和冲击射流数值模拟[J]. 推进技术, 2001, 22(1): 43-46. DOI: 10.3321/j.issn:1001-4055.2001.01.012.
HE Feng, XIE Junshi, HAO Pengfei, et al. Computation of axisymmetric jet flow with Spalart-Allmaras turbulence model[J]. Journal of Propulsion Technology, 2001, 22(1): 43-46. DOI: 10.3321/j.issn:1001-4055.2001.01.012.
[8] 苏晓鹏, 钱林方, 戴劲松.带炮口装置时某火炮膛口流场数值仿真[J].计算机仿真, 2009, 26(9): 15-18. DOI: 10.3969/j.issn.1006-9348.2009.09.007.
SU Xiaopeng,QIAN Linfang,DAI Jinsong. Muzzle flow field simulation of gun with a muzzle attachment [J]. Computer Simulation, 2009, 26(9): 15-18. DOI: 10.3969/j.issn.1006-9348.2009.09.007.
[9] JIANG Xiaohai, CHEN Zhihua, FAN Baochun, et al. Numerical simulation of blast flow fields induced by a high-speed projectile[J]. Shock Waves, 2008, 18(3): 205-212. 10.1007/s00193-008-0155-9.
[10]江坤, 王浩. 基于动网格技术的膛口流场数模拟[J].火炮发射与控制学报, 2010, 3: 1-4. DOI: 10.3969/j.issn.1673-6524.2010.03.001.
JIANG Kun,WANG Hao. Numerical simulation of muzzle flow field based on dynamic meshing technique[J]. Journal of Gun Launch&Control, 2010, 3: 1-4. DOI: 10.3969/j.issn.1673-6524.2010.03.001.
[11]代淑兰, 许厚谦, 肖忠良. 带制退器的膛口燃烧流场并行数值模拟[J].弹道学报, 2009, 21(4): 84-87.
DAI Shulan,XU Houqian,XIAO Zhongliang. Numerical simulation of gun muzzle flow field including movable boundary[J]. Journal of Ballistics, 2009, 21(4): 84-87.
[12]LOVE E S. Initial inclination of the mixing boundary separating an exhausting supersonic jet from a supersonic ambient stream[J]. Ugeskrift for Laeger, 1999, 161(36):5038-5039.
[13]高树滋, 赵润祥, 马大为. 火炮计算流体力学[M].北京: 兵器工业出版社, 1995: 165-172.
GAO Shuzi, ZHAO Ruixiang, MA Dawei. Cannon computational fluid dynamics[M]. Beijing: Weapons Industry Press, 1995: 165-172.
[14]乐贵高, 马大为, 冯勇,等. 某火炮膛口流场数值仿真[J]. 兵工学报, 2004, 25(1):19-22. DOI: 10.3321/j.issn:1000-1093.2004.01.005.
LE Guigao, MA Dawei, FENG Yong, et al. Numerical simulation of muzzle blast flowfields of large caliber guns[J]. Acta Armamentarii, 2004, 25(1):19-22. DOI: 10.3321/j.issn:1000-1093.2004.01.005.
[15]刘昕, 姜宗林, 王春,等. 欠膨胀超声速射流不稳定性机理的数值研究[J].力学学报, 2008, 40(5): 577-584.
LIU Xin, JIANG Zonglin, WANG Chun, et al. Numerical investigation into the mechanism of under-expanded supersonic jet instability[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(5): 577-584.
[16]翁春生,王浩.计算内弹道学[M].北京:国防工业出版社,2006.
WENG Chunsheng, WANG Hao. Computing interior ballistics[M]. Beijing: National Defense Industry Press, 2006.
[17]陶如意,孙继兵,黄明,等. 高低压室平衡炮内弹道数值模拟及试验研究[J]. 南京理工大学学报, 2006, 30(4): 478-485. DOI: 10.14177 /j.cnki.32-1397n. 2006.04.019.
TAO Ruyi, SUN Jibing, HUANG Ming, et al. Interior ballistics numerical simulation and experiment of balance gun with low and high pressure chamber[J]. Journal of Nanjing University of Science and Technology, 2006, 30(4): 478-485. DOI: 10.14177 /j.cnki.32-1397n. 2006.04.019.
[18]徐流恩, 李永池, 高乐南. 大口径高速平衡炮不同发射药应用探讨[J]. 弹道学报, 2009, 21(2): 15-18.
XU Liuen, LI Yongchi, GAO Lenan. The application discussion of propellant in large caliber and high speed counter-mass propelling gun[J]. Journal of Ballistics, 2009, 21(2): 15-18.
[19]王宝元,董文祥,邵小军,等. 弹丸后效期时间和距离测量方法[J]. 兵工学报,2013, 34(10): 1229-1333. DOI: 10.3969 /j.issn.1000-1093.2013.10.021.
WANG Baoyuan, DONG Wenxiang, SHAO Xiaojun, et al. A method for measuring the after-effect duration and operating range of projectiles[J]. Acta Armamentarii, 2013, 34(10): 1229-1333. DOI: 10.3969 /j.issn.1000-1093.2013.10.021.
[20]姜孝海, 范宝春, 李鸿志. 基于ALE 方程的动网格膛口流场数值研究[J]. 计算力学学报, 2008, 25(4): 563-567.
JIANG Xiaohai, FAN Baochun, LI Hongzhi. Numerical investigation on the muzzle flow with dynamic mesh based on ALE equation[J]. Chinese Journal of Computational Mechanics, 2008, 25(4): 563-567.
Themuzzleflowfieldinducedbyhyper-velocityprojectile
LI Zijie, WANG Hao, CHEN Jianwei
(School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)
To analyze the muzzle flow field of hyper-velocity projectile, we established a 2-D axisymmetric numerical simulation model based on the finite volume method. The Navier-Stokes equations are solved on an extended mesh covering the whole computational domain. The holistic movement of a partitioned mesh processing method and realizablek-epsilon turbulence model is used coupling the process of interior ballistic and the Six-DOF UDF program which controls the projectile moving. Taking the 300 mm balanced gun as an example, the simulation results indicate here that the initial flow field has been formed clearly when the projectile is 3.3 m away from muzzle, and the pressure is about 3.8 MPa when the shock wave gets to the muzzle. It is noteworthy that the propellant gas velocity reaches 2 500 m/s but it is still unable to catch up and surround the projectile. So the impact of muzzle flow on the hyper-velocity projectile movement is different from the impact on the low-speed projectile. Subsequently it is formed a completely wave system composed of the multilayer shock wave including coronary blast, shock wave, reflected shock wave, Mach disk and the discontinuity surface, which makes the wave structure and the jet flow field more obvious.
hyper-velocity projectile; muzzle flow field; dynamic mesh; 2-D axisymmetric; characteristic analysis
10.11918/j.issn.0367-6234.201605088
V211.3
A
0367-6234(2017)10-0053-07
2016-05-20
国家自然科学基金(51305204)
李子杰(1990—),女,博士研究生;
王 浩(1961—),男,研究员,博士生导师
王 浩,wanghao@mail.njust.edu.cn
(编辑张 红)

