基于PMU的分布式次同步振荡在线辨识方法
陈 剑 周宇植
基于PMU的分布式次同步振荡在线辨识方法
陈 剑1周宇植2
(1. 国家电网江苏省电力公司生产技能培训中心,江苏苏州 215004;2. 国家电网江苏省电力公司苏州供电公司,江苏苏州 215004)
为减轻WAMS主站端的软硬件开销,同时也为了避免WAMS主站端对PMU数据进行采样时产生的频率混叠现象,本文在分析了WAMS/PMU通信架构和同步相量测量的算法原理的基础上,提出了在PMU装置上实现分布式次同步振荡在线参数的辨识方法。本文深入分析和比较了两种不同的参数辨识方法,基于相量数据的次同步振荡参数辨识方法和基于原始采样值的次同步振荡参数辨识方法,讨论了基于相量数据的次同步振荡参数辨识方法的局限性,指出了基于原始采样值的次同步振荡参数辨识方法,既可避免对次同步振荡分量的误判,提高次同步振荡分析监测的准确性和适应性,同时又更易于实现超同步振荡等扩展性应用需求。
次同步振荡;分布式测量;FFT;同步相量测量单元
我国经济的不断发展促进了电网规模的不断扩大,大容量、远距离输电是我国电力系统发展的客观需求。为提高线路输送能力、控制并行线路之间的功率分配、增强电力系统暂态稳定性,电力系统中安装了串联补偿装置、高压直流(HVDC)控制系统、动态无功补偿装置等设备。然而,这些设备和技术的发展也带来了次同步振荡问题[1]。电网次同步振荡对发电机组和系统稳定危害很大,当次同步振荡频率与发电机组扭振的固有频率满足特定互补关系时可引发发电机组轴系扭振迅速增大甚至机组轴系损坏事故。及时发现并采取措施抑制系统中的次同步振荡[2-4],是保障电力系统安全、稳定运行亟待解决的关键问题之一。
基于同步相量测量技术的广域测量系统(wide area measurement system, WAMS)在电网安全稳定运行中扮演着越来越重要的角色,它在动态监测、动态安全分析和控制、状态估计等方面取得了广泛的应用[5],同步相量测量单元(phasor measure unit,PMU)作为WAMS子站系统的核心担负着原始数据采集、测量和传输的任务。尤其是近年来,随着低频振荡、次同步振荡等现象的增加,PMU为各网省级调度中心在基于WAMS系统基础上分析各振荡现象时提供了高精度、高密度原始数据源,因此日益取得了广泛重视。但随着电网规模的不断扩大,PMU布点数目的不断增多,使得网络结构日益复杂,一方面在WAMS主站端进行低频振荡、次同步振荡分析将会大大增加WAMS主站端的软硬件开销,另一方面由于WAMS主站对PMU数据采样存在的频率混叠现象,使得在WAMS主站分析次同步现象存在一定的弊端[6]。
因此,本文通过对PMU采样的原始电流数据进行频谱分析,从而准确计算出次同步振荡的频率成分,实现了次同步振荡参数的辨识与告警。并与文献[6]提出的“对PMU测量的相量数据进行频谱分析的方法”进行了对比,尤其深入分析了在幅值调制的动态条件下两种辨识方法的区别,指出了通过对原始采样数据进行分析,既可避免对次同步振荡分量的误判,提高次同步振荡分析监测的准确性和适应性,同时又更易于实现超同步等扩展性应用需求。
1 WAMS/PMU系统构架
文献[7]阐述了国内的WMAS/PMU系统采用通信网络结构,其中,PMU子站采用TCP/IP协议通过电力数据调度网按照WAMS主站下发的传输频率向WAMS主站以恒定频率实时发送动态数据,其网络结构如图1所示。
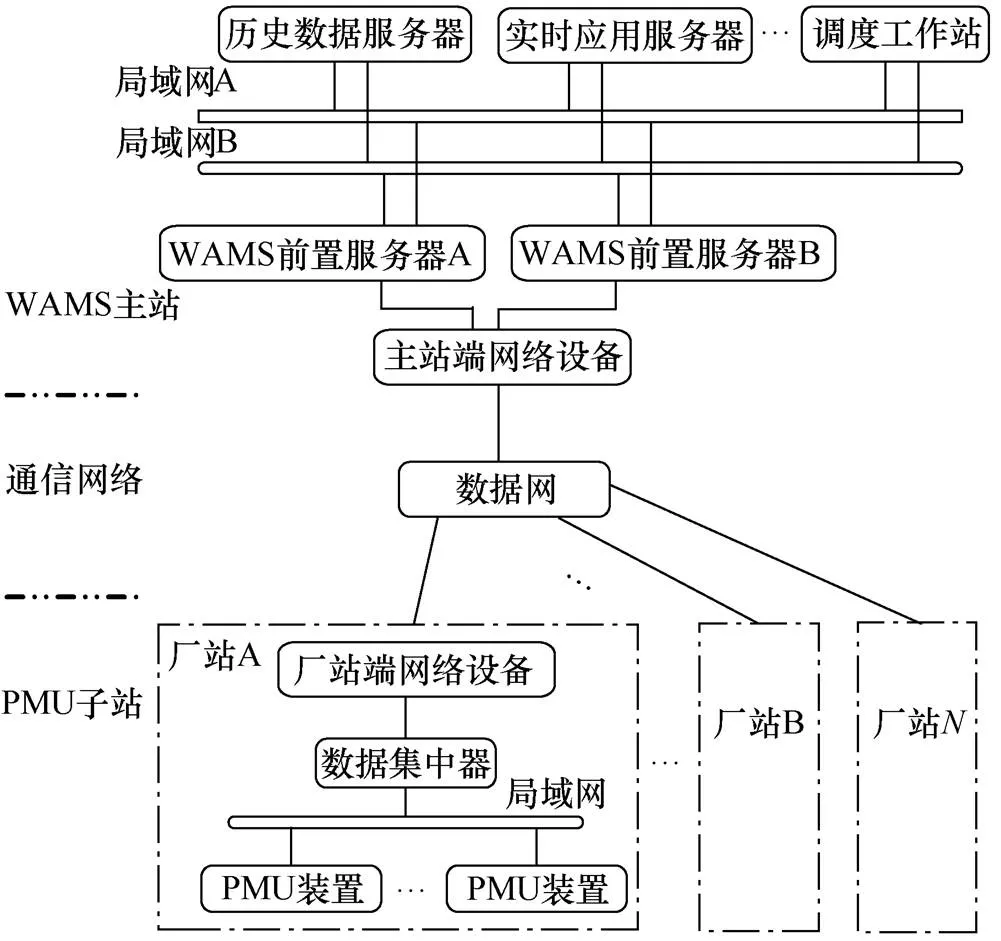
图1 WAMS/PMU系统构架
在该架构下,WAMS主站对PMU的数据也是一个数据采样频谱分析的过程,其采样率即为PMU上送同步相量的速率。IEEE Std C37.118—2011规 定[8],其传输速率最高为100Hz。但实际工程应用中,国内大多采用了50Hz甚至25Hz的传输速率。以25Hz为例,根据香农采样定律,WAMS主站在取得PMU数据后,只能分析出不超过12.5Hz的次同步振荡分量。因此,这极大限制了在WAMS主站分析次同步振荡现象的应用前景。
2 次同步振荡对PMU的测量影响
电力系统次同步振荡是电力系统中的电气系统与发电机组以低于同步频率的某个或多个自然振荡频率交换能量的一种不正常运行状态。电力系统中安装的串联补偿装置、高压直流(HVDC)控制系统、动态无功补偿装置等设备均有可能引起次同步振荡问题[9]。文献[6]指出,无论是何种产生机理,对于PMU装置而言,产生次同步振荡时均表现为所测量的电流信号中叠加了次同步振荡分量。其数学模型为

式中,0为基波频率;为各次同步振荡分量的频率;1为基波信号初相角;为各次同步振荡分量的初相角;为基波的幅值;DA为各次同步振荡分量幅值。频率范围通常在低频振荡频率(0.2~2.5Hz)和同步频率(50Hz)之间。
文献[10]中,作者对使用DFT方法计算相量的方法做了详细的推导,文中指出对于含有谐波输入的信号为
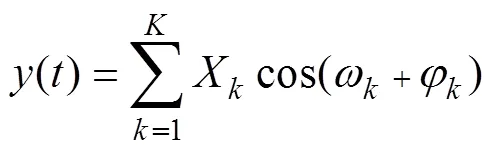
其相量计算结果中会存在0+和0的频谱分量,其中0频谱分量的幅值最大。由此,可以推导出,对于式(1)所示的含有次同步分量的输入信号而言,其PMU相量结果中将存在0+和0的频谱分量,这为使用PMU相量结果进行FFT分析,从而得到次同步分量的频率和幅值奠定了理论基础。
3 基于相量数据的次同步振荡参数辨识
3.1 辨识流程
文献[6]基于相量数据实现了次同步振荡参数的辨识和告警,其辨识流程如图2所示。

图2 次同步振荡分析辨识流程
本文对文献[6]提出的“基于相量数据分析次同步振荡参数”的方法进行了如下Matlab仿真。其中根据FFT基本理论,FFT的频率分辨率为

本文中,选取s=100Hz、=256,则频率分辨率可达0.390625Hz。图3是对含有幅值为0.1,频率为15Hz的次同步分量信号的PMU相量数据进行FFT分析结果的Matlab仿真图,其原始信号为
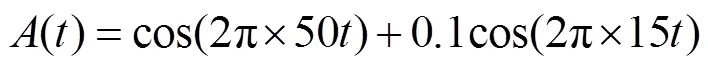
由图3可知,PMU相量中含有35.55Hz的频率分量,因此次同步振荡的频率为14.45Hz。

图3 次同步振荡参数辨识
3.2 幅值调制的影响
IEEE Std C37.118—2011标准对PMU的动态性能提出了明确的规范要求[11],幅值调制是其中的一种,其定义为

式中,a为幅值调制深度;a为调制频率。本文选择如下信号对其PMU测量相量进行FFT频谱分析,其幅值调制深度为0.1,调制频率为5Hz。

其FFT频谱分析结果如图4所示。

图4 幅值调制的FFT频谱分析
根据FFT的频谱分析结果,在相量数据中存在5.469Hz的频谱分量,根据基于相量数据的次同步振荡辨识流程,PMU装置将认为系统中存在44.531Hz的次同步振荡分量,但实际系统中则是5Hz的幅值调制信号。因此在幅值调制的条件下,根据PMU相量数据进行FFT频谱分析从而辨识次同步振荡分量参数会出现异常。由此可见,在幅值调制的条件下,基于相量数据的次同步振荡参数辨识将会引起装置的误判,从而实现错误的次同步振荡振荡告警。
4 基于原始采样值的次同步振荡参数辨识
4.1 辨识流程
如前所述,对于PMU装置而言,产生次同步振荡时均表现为所测量的电流信号中叠加了次同步振荡分量,因此可对电流输入信号做FFT分析,从而计算出次同步振荡分量的频率和幅值。因此本文修改了文献[6]提出的PMU相量计算模型,如图5所示。

图5 基于原始采样值的次同步振荡参数辨识
4.2 FFT频谱分析
基于原始采样值的次同步振荡参数辨识方法其优点是在进行FFT频谱分析后,可直接根据其频谱的频率分量判断出次同步振荡的频率分量,这是与基于PMU相量数据进行次同步振荡参数辨识方法不同之处。也正是因为如此,幅值调制对基于原始采样值的次同步振荡参数辨识没有任何影响。因此避免了对次同步振荡分量的误判,提高了次同步振荡分析监测的准确性和适应性。本文选取的采样率为200Hz,采样点数512点,则根据式(3),可得其频率分辨率为0.390625Hz。再根据香农采样定理该方法可分析输入频率最高为100Hz的输入信号,因此,基于原始采样值的FFT分析方法还可用于分析50~100Hz之间的超同步振荡现象,若进一步提高采样频率,则可分析更高频率的超同步振荡分量。
本文对式(6)所示的信号直接进行了FFT频谱分析,其结果图6所示。可知,基于原始采样值的次同步振荡参数辨识方法正确的识别出了振荡分量。

图6 FFT频谱分析结果
5 结论
随着电网规模地不断扩大,电力系统中安装的串联补偿装置、高压直流(HVDC)控制系统、动态无功补偿装置等设备有可能会引起电力系统次同步振荡等现象。而随着PMU布点数目的不断增多,使得WAMS主站端的软硬件开销越来越多,因此提出了在PMU装置上实现分布式的次同步振荡参数在线辨识方法,指出了与基于相量数据的次同步振荡参数辨识方法相比,基于原始采样值的次同步振荡参数辨识方法更适合进行次同步振荡参数辨识,而且其扩展性更好。但对数据直接进行FFT分析,其结果精度尚不是很高,还需做进一步研究,以提高FFT算法的频谱分析精度。
[1] 徐政, 罗惠群. 电力系统次同步振荡问题的分析方法概述[J]. 电网技术, 1999, 23(6): 36-39.
[2] 张学群, 康积涛, 李林, 等. 基于SVC利用远端信号缓解次同步谐振研究[J]. 电气技术, 2010, 11(12): 21-23.
[3] 蔡婷婷, 徐青山, 刘瑜俊, 等. TCR型SVC抑制电力系统次同步振荡研究[J]. 电测与仪表, 2015(15): 26-33.
[4] 李伟, 肖湘宁, 赵洋. 无功发生源抑制次同步振荡的机理分析[J]. 电工技术学报, 2011, 26(4): 168-174.
[5] 许树楷, 谢小荣, 辛耀中. 基于同步相量测量技术的广域测量系统应用现状及发展前景[J]. 电网技术, 2005, 29(2): 44-49.
[6] 张敏, 沈键, 侯明国, 等. 相量测量单元实现次同步振荡在线辨识和告警的探讨[J]. 电力系统自动化, 2016, 40(16): 143-152.
[7] 侯明国, 沈健, 檀永, 等. 相量测量装置实时数据的三段式变频传输方法[J]. 电力系统自动化, 2015(21): 93-98.
[8] IEEE Std C37.118 Standard for Synchrophasor Measurements for Power Systems[S]. 2011.
[9] 王亮, 谢小荣, 姜齐荣, 等. 大规模双馈风电场次同步谐振的分析与抑制[J]. 电力系统自动化, 2014, 38(22): 26-31.
[10] 沈健, 周斌, 汪昀, 等. 提升PMU动态测量性能的若干方法[J]. 电力系统保护与控制, 2015, 43(19): 89-94.
[11] 毕天姝, 刘灏, 杨奇逊. PMU算法动态性能及其测试系统[J]. 电力系统自动化, 2014, 38(1): 62-67.
On Line Identification Method of Sub Synchronous Oscillation based on Distributed PMU
Chen Jian1Zhou Yuzhi2
(1. State Grid Jiangsu Technican Training Center, Suzhou, Jiangsu 215004; 2. State Grid Suzhou Power Supply Company, Suzhou, Jiangsu 215004)
In order to reduce the overhead of software and hardware of WAMS main station, and to avoid the frequency aliasing, this article imposed an method of online parameter identification on sub synchronous oscillation, based on the analysis of the communication architecture of WAMS/PMU system and the principle of synchronized phasor measurement algorithm. Two different parameter identification methods are analyzed and compared in this paper, including parameter identification method based on phasor data and parameter identification method based on the original sample value. The limitations of the parameter identification method based on phasor data are discussed in this paper. It pointed out that the parameter identification method based on the original sample value avoids miscarriage of justice of the sub synchronous oscillation, and improves the accuracy and adaptability of the analysis and monitoring of the sub synchronous oscillation.
sub synchronous oscillation;distributed measurement;FFT;PMU
陈 剑(1972-),女,本科,工程师,主要研究方向:智能变电站二次运维及变电站自动化。

