Spark计算节点同构环境下Executor的内存分配优化模型

(重庆市北碚区中医院 重庆 400700)

Spark计算节点同构环境下Executor的内存分配优化模型

朱蓉

(重庆市北碚区中医院重庆400700)

在对Spark云计算平台的作业执行机制进行研究分析的基础上，针对目前Spark处理作业时Executor的人为请求资源机制，提出了一种Spark计算节点同构环境下Executor所需内存资源的优化分配算法，该算法能够基于处理数据的数据量对分布式内存资源进行弹性分配，达到了Spark在数据量变化情况下合理利用分布式内存资源这一目的，并对此进行了仿真实验验证。

Spark；Executor；内存资源；资源分配

一、前言

近几年来，云计算技术成为人们讨论的热点，随着云计算研究的不断深入和发展，Spark大数据处理平台受到了越来越多的关注。通过依靠Scala强有力的函数式编程、Actor通信模式、闭包、容器、泛型等手段，借助统一资源分配调度框架Mesos和YARN[2]，并融合了MapReduce和Dryad[3]等技术，使得Spark站在巨人的肩膀上，成为一个简洁、直观、灵活、高效的分布式大数据处理框架。

本文对Spark中任务调度和资源分配机制进行了研究，提出了一种基于计算节点同构，即计算节点硬件环境一致下的资源分配优化算法SMAO(Spark’s memory allocation optimizing)，能够基于作业的数据量对分布式内存资源进行弹性分配，达到内存资源合理分配的目的，并对此进行了仿真实验验证。

二、Spark内存计算框架

Spark在实时计算方面速度卓越的一个核心原因就是因为有统一的RDD(Resilient Distributed Datasets，弹性分布式数据集)，Spark中使用了RDD抽象的分布式计算，即使用RDD对应的transform/action等操作来执行分布式计算；并且基于RDD之间的依赖关系组成lineage以及checkpoint等机制来保证整个分布式计算的容错性[4]。与Hadoop不同，Spark一开始就瞄准性能，将数据(包括中间结果)放在内存中进行计算，并且将用户重复利用的数据也缓存到内存中进而提高计算效率，因此Spark尤其适合迭代型和交互性任务的计算，虽然Spark架构下的计算需要大量的内存，但其性能可随着机器的数目呈现线性的增长，其内存计算速度比Hadoop的MapReduce要快100倍左右[5]。下面我们先看一下RDD，再对Spark运行架构进行了解。

(一)弹性分布式数据集

在Spark中一切运算都是以RDD为基础和核心的，而RDD的核心是RDD的分区存储和RDD的有向无环图的执行[6]。在提交Job后，Spark依照对Job分解后的RDD之间的依赖关系形成Spark的调度顺序，并结合任务的分发、跟踪、执行等过程，最终形成了整个的Spark应用程序的执行。

(二)Spark的应用程序执行机制

Spark应用程序的执行是基于SparkConf、SparkContext等环境信息的，在Spark 1.3.0中，可以人为设置参数spark.Executor.memory的大小来定义每一个Executor所需的内存资源生成SparkConf配置变量，并通过val sc=new SparkContext(new SparkConf())来实例化该应用程序的SparkContext上下文信息，Driver主控进程会在SparkContext中构建DAGScheduler等重要对象，负责对应用进行解析、stage切分并调度Task到Executor执行。

Executor的运行[8]是通过Spark的Akka消息机制向Master注册程序后发送SparkConf配置信息给Worker进而触发启动的。在Master的消息响应中会调用schedule方法和launchExecutor方法，在schedule方法中要启动Driver程序，然后调用Worker，而在launchExecutor内部，Master会发送消息(消息即为LaunchExecutor)给Worker节点让它发起一个Executor，从Spark1.3.0的Executor消息处理源码可以看出，ExecutorRunner负责分配Worker节点请求的CPU核数和Memory大小，实时地维护executor进程，并负责executor的开始和消亡。

三、采用SMAO对Executor内存请求量进行弹性分配

Executor执行所占用内存基本上是Executor内部所有任务共享的，而每个Executor可以支持的任务的数量取决于Executor所管理的CPU Core资源和内存资源的多少，目前的资源分配方式是是用户了解每个任务的数据规模的大小，主观地推算出每个Executor大致需要多少内存和CPU。而在一般应用中，Spark需要处理的数据量大小是变化的，比如本论文的基金项目中使用Spark来分析三峡库区的水质监测数据，我们提出一种Spark计算节点同构环境下的Executor内存资源分配的优化模型，能够基于监测数据量对Spark计算节点Executor所需的分布式内存资源进行弹性分配，达到内存资源合理分配的目的，如下描述:

Executor所消耗的内存，除了用于RDD数据集本身的开销，还包括算法所需各种临时内存空间的使用，即

SE≈SR+Sn

(1)

SE表示Executor所消耗的内存，SR表示Executor中RDD数据集所占用的空间大小，Sn表示算法执行所需要的各种空间，包括JVM的临时空间消耗等各种计算消耗。默认情况下，Spark采用整体物理内存(spark.executor.memory)的60%来管理SR产生的RDD Cache数据，这表明在任务执行期间，最多有40%的内存可以给Sn用来保证任务运行，用户可以通过设置参数spark.storage.memoryFraction来改变这个比例大小。在使用Executor的过程中，如果数据量增大或分配的SR不够则会报程序运行空间不足，如果分配的Sn不够，则会影响GC效率甚至报java.lang.OutOfMemoryError:Java heap space的错误。用SF来表示频繁发生Full GC时候的Sn的临界值，在对Executor内存资源分配时候中要保证以下条件：

k*SE≥SR,且(1-k)*SE≥SF

(2)

k表示参数spark.storage.memoryFraction，用户可以自己设置这个参数来调整SR和Sn的比例。

用SF作为Sn的临界值的时候，公式(1)变为

SE≈SR+SF

设X为原始数据的数据量，原始数据经HDFS文件系统再转换为Spark环境下的RDD数据集的转换，RDD数据集所占空间即SR与原始数据的数据流大小呈现线性关系：

SR=p1X+p2

(3)

而算法执行所需要的的开销Sn包含数据集本身的开销及各种算法的开销，算法不同，开销也不同，虽然这种开销难以统计。但是Sn与SR近似地呈现出Spark程序算法的空间复杂度的关系，也就意味着临界值SF与原始数据X也近似地呈现Spark程序算法的空间复杂度的关系。对于SR，可以将RDD cache在内存中，从Spark的log日志输出或者UI输出中可以看到每个Cache分区的大小，从而计算某数据量对应的SR，对于SF，可以使用测试GC的方法来获得。

本文提出一种Spark计算节点同构情况下的Executor执行时的内存消耗优化算法SMAO(Spark’s memory allocation optimizating)，计算步骤如下：

1.根据该应用程序所运行的作业量及RDD内存消耗量的历史记录SR采用最小二乘法拟合得到公式(3)的参数p1和p2，进而计算下一个作业的任务量X’对应的SR’。

2.计算Spark所运行的该应用程序所消耗RDD的空间复杂度S(X)，根据该应用程序所运行的历史作业的SF，进而计算下一个作业X’，所产生的SF’。

3.由SR和SF代入公式1和公式2，计算SE’

4.在计算节点同构情况下，对Spark提交下一个作业时候可以使用SE’的资源量作为每一个Executor的内存分配请求，此时的SE’即Executor的内存优化分配的阈值。

此优化算法相比没有使用该算法优化而言，使得Spark在处理数据时候随着数据量的变化而弹性分配内存资源，达到内存资源合理分配的目的，下面将进行仿真实验。

四、算法仿真与分析

(一)仿真实验环境及数据集

实验环境为由搭建的3个节点组成的虚拟机集群环境，使用ubuntu-12.04的64位版本的linux操作系统，产生一个主节点nameNode和两个从节点dataNode1和dataNode2。虚拟机nameNode主节点的内存为4GB，处理器数量为2，双核，两个dataNode内存为2GB，处理器数量为2，单核。Java版本为JDK1.7.0_71，Hadoop的版本为2.4.0版本，Spark版本为1.3.0，实验的程序是根据Spark自带的PCA程序而改写的带有标准化处理的PCA程序(SNPCA,Spark’s Normalized Principal Component Analysis)。

前面讲过，在Executor中所消耗的内存，除了用于RDD数据集本身的开销外，还包括算法所需各种临时内存空间Sn的使用，SF表示频繁发生Full GC时候的Sn的临界值，SF受系统环境影响，我们可以假设实验程序SNPCA引起的SF开销符合以下空间复杂度：

S(x)=q1x3+q2x2+q3x+q4

(4)

使用最小二乘法对SF的历史数据来进行多项式拟合，进而计算后三个测试集数据[131,143,155]MB实际的SF量为[361,379,482]MB，而依照SMAO算法计算得[414.9,498.5,599.1]MB，对比如下：

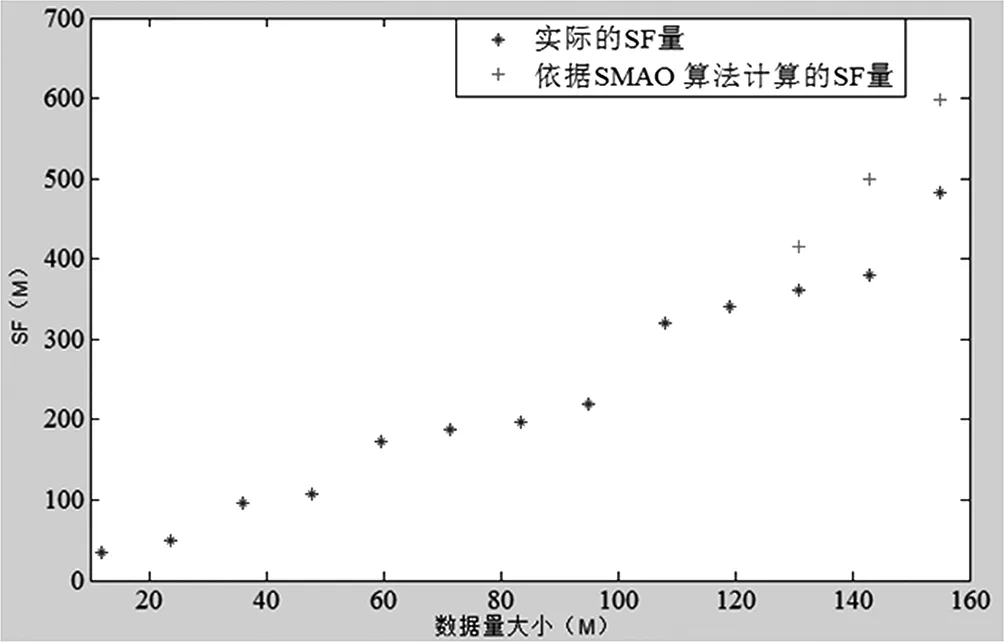
实际的SF量与依据SMAO算法计算的SF量对比图

使用最小二乘法对SF的历史数据来进行多项式拟合的结果，即公式4的系数为：[0.0002,-0.0347,4.0694,-17.0236]，也能看出来实验程序SNPCA算法的空间复杂度基本上还是一个线性函数。

计算出SR量和SF量后，可以依照公式1、公式2计算计算节点同构环境下的SE’，但是对于实验的SNPCA程序，Executor中SF开销与原始数据量呈线性关系，并且SR与数据量X(公式1)也是线性关系，所以此时Executor的分配量与数据量也呈线性关系，所以仍然可以使用公式4对数据量X’和Executor的开销SE’进行分析，为充分起见，可以对Executor的内存分配“盈余”一定比例，比如“盈余”0.1时，取Executor内存优化分配量为1.1*SE’，来充分提供除

(二)实验结果分析

理论上给Executor的内存分配当然是多多益善，实际受机器配置、以及运行环境、资源共享、JVM GC效率等因素的影响难以具体衡量，但是还是可以使用SR和SF的历史数据来进行内存合理分配。

从以上可以看出，依据SMAO算法计算的SR与实际大小相比几乎一样，Spark在作业处理时候的内存消耗量除了RDD数据集本身的SR开销之外，还包括所需各种临时内存空间的使用带来的其他消耗量SF。

需要注意的是，SMAO算法目前应用于计算节点同构的情况下，SRAO算法的使用需要预先知道Spark应用程序产生RDD数据集的空间复杂度，因此对于不同的作业程序，需要人为地事先计算空间复杂度，另外，如果Executor执行的时候频繁发生Full GC，可以考虑减小这个spark.storage.memoryFraction比值来减少Full GC发生的次数，来改善程序运行的整体性能。

五、结束语

本文首先对Spark的架构和应用执行机制进行了介绍，并引出了Spark 1.3.0在Executor的内存分配方面还不太令人满意，目前采用的是人为的任务分配机制，针对此问题，提出了基于Spark的同构计算节点环境下Executor的内存分配优化算法，并展开实验验证该优化方案，实验结果显示优化方案的有效性。

[1]http://spark.apache.org/.Accessed Oct,2015

[2]Hindman B,Konwinski A,Zaharia M,et al.Mesos:A Platform for Fine-Grained Resource Sharing in the Data Center[C].NSDI.2011,11:22-22.

[3]Isard M,Budiu M,Yu Y,et al.Dryad:distributed data-parallel programs from sequential building blocks[C].ACM SIGOPS Operating Systems Review.ACM,2007,41(3):59-72

[4]Zaharia M,Chowdhury M,Das T,et al.Resilient distributed datasets:A fault-tolerant abstraction for in-memory cluster computing[C]//Proceedings of the 9th USENIX conference on Networked Systems Design and Implementation.USENIX Association,2012:2-2.

[5]Zaharia M,Chowdhury M,Franklin M J,et al.Spark:cluster computing with working sets[C]//Proceedings of the 2nd USENIX conference on Hot topics in cloud computing.2010:10-10.

[6]Zaharia M,Chowdhury M,Das T,et al.Resilient distributed datasets:A fault-tolerant abstraction for in-memory cluster computing[C].Proceedings of the 9th USENIX conference on Networked Systems Design and Implementation.USENIX Association,2012:2-2.

[7]高彦杰.Spark大数据处理技术、应用与性能优化[M].北京：机械工业出版社，2014

[8]王家林.大数据Spark企业级实战[M].北京：电子工业出版社，2015