同心异径管最佳超应变度研究

，

2(1.西南石油大学 机电工程学院， 四川 成都 610500; 2.沐川县高笋乡人民政府， 四川 乐山 614504)

同心异径管最佳超应变度研究

陶春达1，钟云龙

2(1.西南石油大学 机电工程学院， 四川 成都 610500; 2.沐川县高笋乡人民政府， 四川 乐山 614504)

基于同心异径管的轴对称性建立了相应的力学模型，计算了同心异径管在32.0 MPa工作内压作用下的应力，讨论了同心异径管的径向、轴向、周向和相当应力的变化特征，确定了同心异径管应力的危险部位及其变化规律，并分析了基于静强度的同心异径管的最佳超应变度,得到了最佳自增强压力。对于以静强度失效为主要失效形式的同心异径管 R(C)-100×50-Sch80S, 其最佳自增强内压为64.3 MPa，危险点所对应的最佳超应变度为73.08%。

异径管； 应力； 有限元计算； 超应变度； 自增强

异径管俗称大小头，常用于石油、化工及制药等装置中，通常在高温、高压和腐蚀环境中工作。因此，时有失效破坏出现，并带来一定的人员伤亡和财产损失，对安全生产带来了很大的影响[1]。目前国内外对异径管的分析研究报道还不多[1-6]，这些报道中既有理论分析，还有实验研究，但对如何提高异径管强度的研究较少。

对于承受高温、高压和在腐蚀环境中工作的异径管，提高强度的措施之一就是对其实施自增强处理[7-12]。其原理是对服役前的设备施加比工作压力高得多的内压，使其内壁产生塑性变形，外壁产生弹性变形。由于塑性变形不可恢复而弹性变形可以恢复，故卸载后在内壁上形成有利的残余应力分布，内壁面为较高的压应力而外表面为较低的拉应力。由于构件的危险部位在内表面的应力集中处，故残余压应力的存在使得构件危险部位的工作应力降低，构件的强度得以大幅度提高。

异径管通常可分为同心异径管、偏心异径管和异径弯管3种形式。偏心异径管和异径弯管几何构成和应力分布较复杂，文中仅对结构相对简单的同心异径管进行了分析研究，找出同心异径管径向、轴向、周向和相当应力的分布规律后来确定应力危险点，并对内压作用下同心异径管的最佳超应变度进行了分析，确定了同心异径管自增强处理的最佳超应变度，以期大幅度提高异径管的强度。

1 同心异径管计算模型

同心异径管R(C)-100×50-Sch80的材料为Q345钢，其弹性模量E=206 MPa，泊松比μ=0.3，公称压力32.0 MPa。

同心异径管大头外径114.3 mm，大头内径97.18 mm，小头外径60.3 mm，小头内径49.5 mm，大头直管段长度25 mm，小头直管段长度15 mm，其结构示意图见图1。

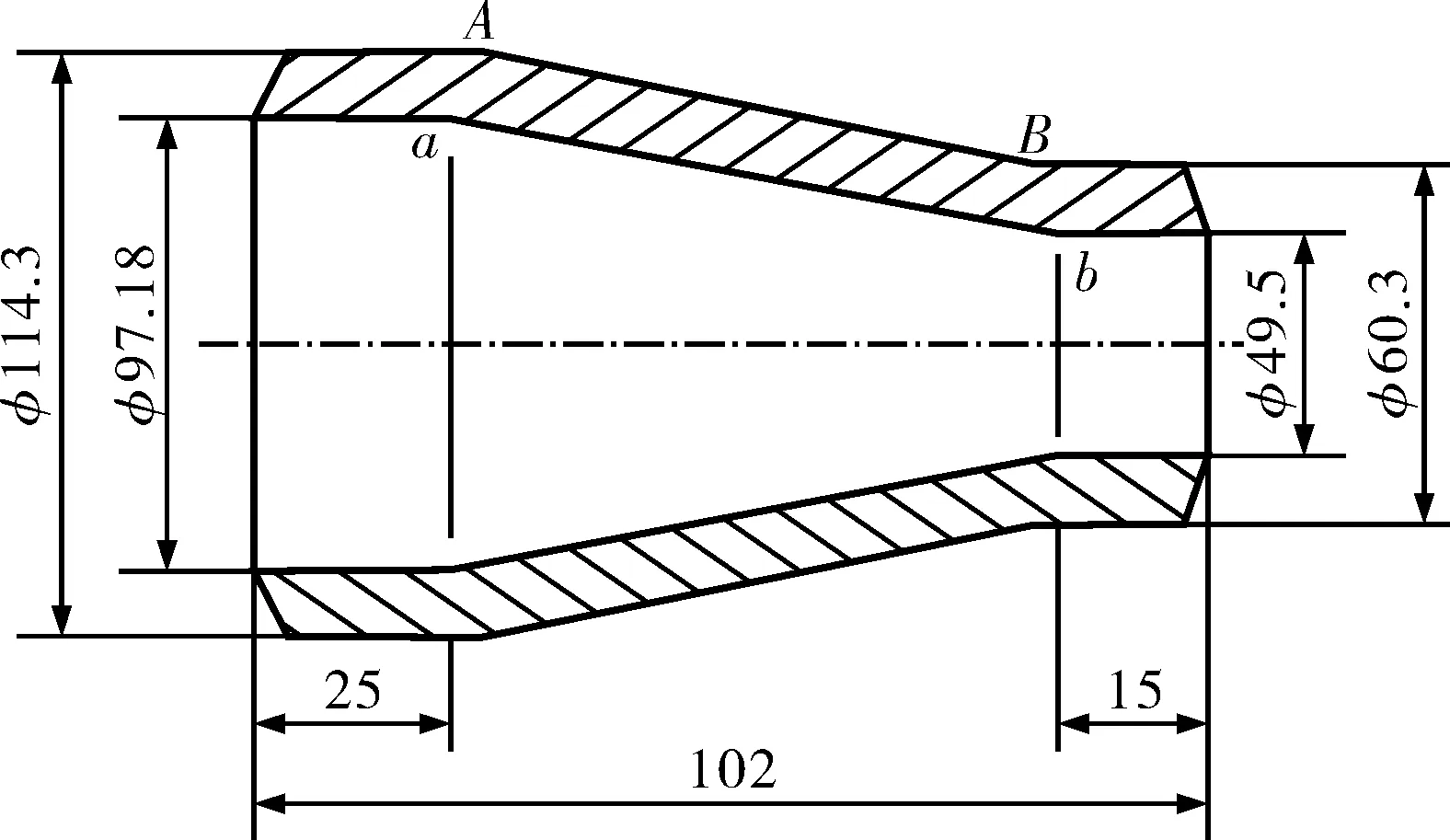
图1 计算示例同心异径管结构示图

根据对称性，取同心异径管的1/4作为研究对象，并对其划分有限元网格，见图2。

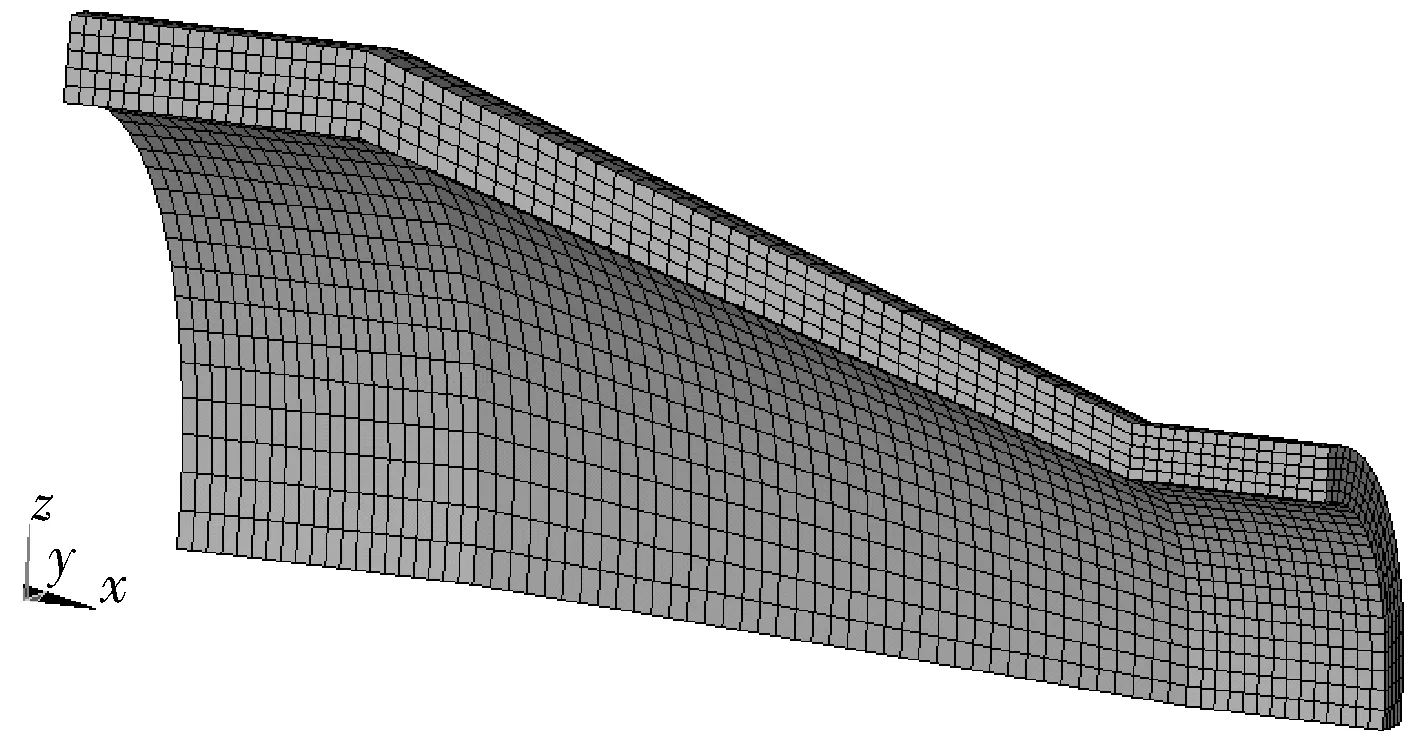
图2 同心异径管模型网格划分

由于对称，在对称面上施加法线方向的约束，在大端直管端面施加轴向约束。本文只对内压作用下的同心异径管进行分析。

2 计算结果分析

2.1

弹性应力分析

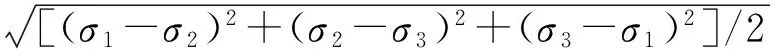
图3 同心异径管模型相当应力分布云图

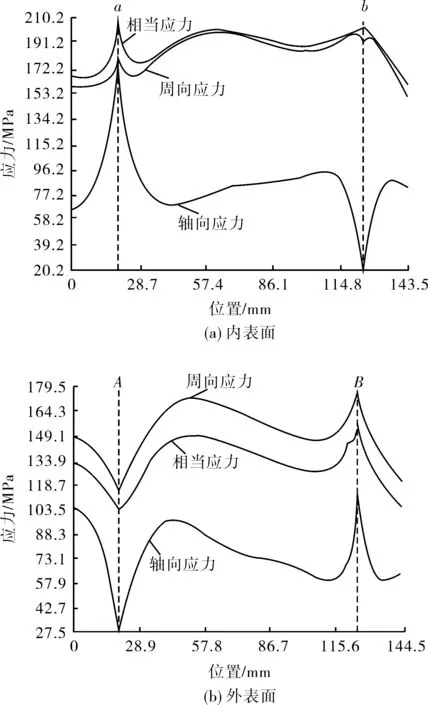
图4 同心异径管模型内、外表面轴向路径上应力分布曲线

由图3、图4可以看出，①同心异径管的各应力分量中，周向应力占主导地位，轴向应力次之，径向应力较小，可以不予考虑。②内表面应力比外表面应力大。③同心异径管变径段大端与小端之间内外表面的相当应力相对较大，内表面的危险点出现在变径段大端与直管段连接部位(图1中的a点)，最大相当应力为210.0 MPa；外表面的危险点出现在变径段小端与直管段连接部位(图1中的B点)，最大相当应力为158.0 MPa。

2.2弹塑性应力分析

针对屈服强度为345 MPa的Q345钢，采用多线性随动强化模型(图5)，利用ANSYS对同心异径管 R(C)-100×50Ⅰ-Sch80S进行弹塑性有限元分析计算。同心异径管内、外表面危险点的周向残余应力随自增强压力的变化曲线见图6。

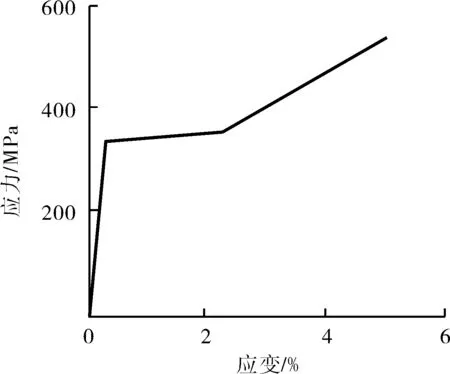
图5 Q345钢应力-应变曲线

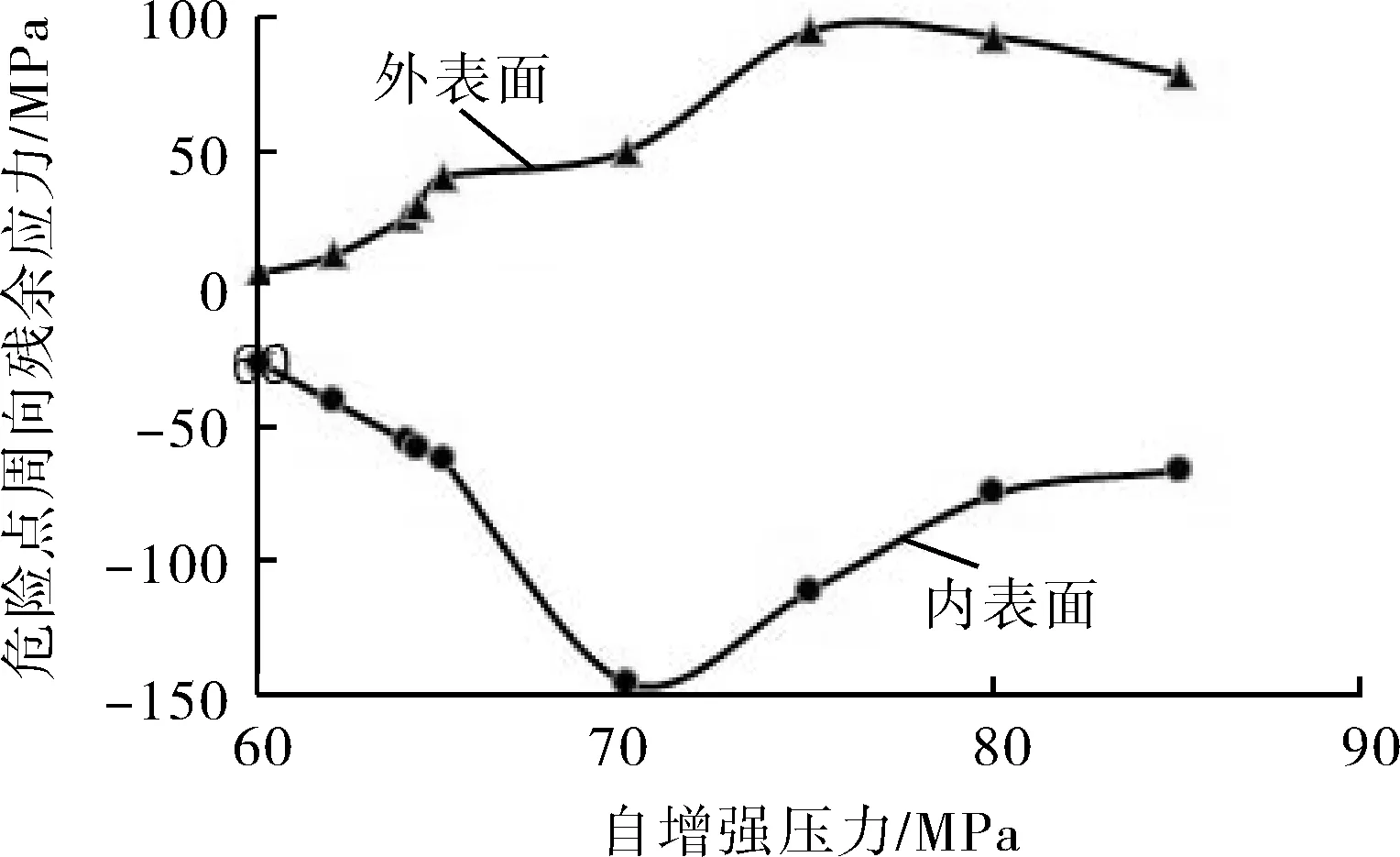
图6 同心异径管模型内、外表面危险点周向残余应力随自增强压力变化曲线

从图6可以看出，内表面产生残余压应力，外表面产生残余拉应力，随着自增强压力的增加，同心异径管内、外表面危险点处的周向残余应力的大小并不是一直增加，增加到一定值后反而减小，可见并不是自增强压力越大残余应力越高。

3 最佳超应变度分析

自增强内压何时为最佳，也就是最佳的自增强超应变度是多少，关于这个问题已经有很多的文献进行了相关的研究[13-17]。

应用第四强度理论可以得到在32.0 MPa工作内压作用下同心异径管内外侧危险点的相当应力分别为(σr)o和(σr)i。自增强处理后, 在同心异径管内侧危险点的残余应力为压应力,外侧危险点的残余应力为拉应力, 残余应力和工作应力的迭加会改变相当应力，使内侧危险点的应力降低，外侧危险点的应力升高。因此，同心异径管内、外侧危险点均有可能成为危险部位, 最佳的超应变度应该是使同心异径管内、外侧危险点有相等的强度, 即有：

(σr)o=(σr)i

(1)

式(1)是基于静强度而提出的确定最佳超应变度的公式。

对于疲劳强度，最佳超应变度就是当内表面和外表面危险点的等效相当应力幅相等时。或者，如果它们不可能相等，就要使危险点的等效相当应力幅值之差达到最小。同心异径管模型内、外表面危险点的相当应力随自增强压力变化曲线见图7。

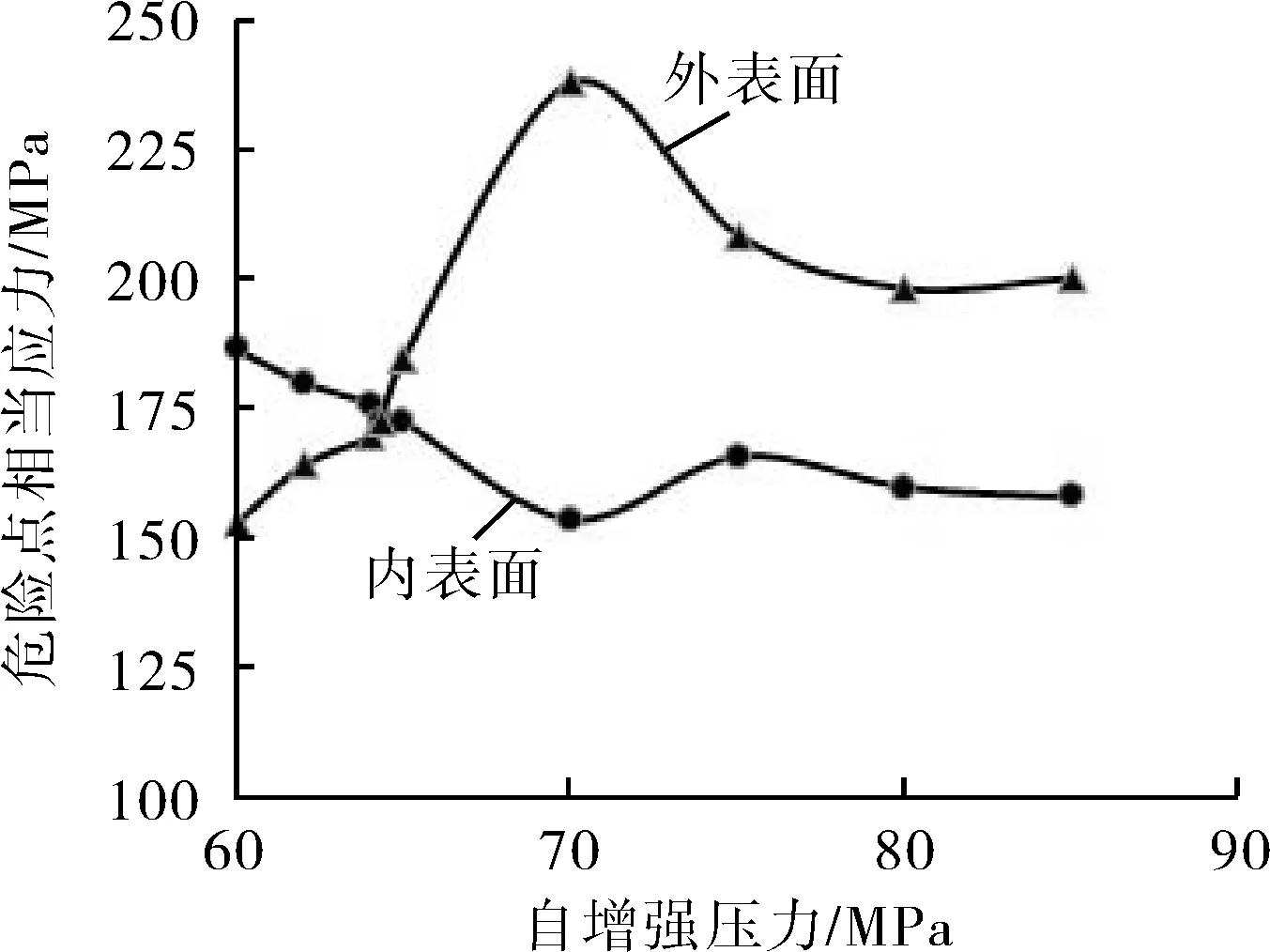
图7 同心异径管模型内、外表面危险点相当应力随自增强压力变化曲线

从图7可以看出，当自增强压力为64.3 MPa、工作压力32.0 MPa时内外表面危险点的相当应力分别为172.12 MPa和172.31 MPa，近似相等。

由式(1)知，此时R(C)-100×50I-Sch80S同心异径管处于最佳的受力状况，64.3 MPa的自增强压力为最佳的自增强压力。通过弹塑性有限元分析，此时危险点处壁厚方向的塑性层厚度为5.35 mm，此处壁厚为7.32 mm，则其最佳的超应变度为φ=5.35/7.32=73.08%。

4 结语

(1)对于R(C)-100×50I-Sch80S同心异径管，在32.0 MPa内压作用下，最大相当应力出现在变径段大端与小端之间。内表面的危险点出现在变径段大端与直管段连接部位，危险点最大相当应力为210.0 MPa；外表面的危险点出现在变径段小端与直管段连接部位，危险点的最大相当应力为158.0 MPa。

(2)同心异径管经自增强处理后其内表面产生残余压应力，外表面产生残余拉应力，随着自增强压力的增加，同心异径管内、外表面危险点处的周向残余应力增加到一定值后反而减小，可见并不是自增强压力越大残余应力越高。

(3)对于R(C)-100×50I-Sch80S同心异径管，其最佳的自增强处理压力为64.3 MPa，此时危险点所对应的最佳超应变度为73.08%。

[1] 陈孙艺.异径管的标准及其失效分析[J].化工设备与管道，2005,42(6)：25-29.

(CHEN Sun-yi. Standard and Failure Analysis of Reducers[J]. Process Equipment and Piping, 2005,42(6)：25-29.)

[2] 陈孙艺，柳曾典.异径管特点的研究及其设计选用[J].石油化工设计,2005,22(3):52-54.

(CHEN Sun-yi，LIU Zeng-dian. Study on the Characteristics of Reducer and Its Selection in Engineering [J]. Petrochemical Design, 2005,22(3):52-54.)

[3] 陈孙艺，柳曾典，陈进. 内压作用下的异径管的应力分析及验证[J].中国机械工程,2007,18(3):365-369.

(CHEN Sun-yi, LIU Zeng-dian, CHEN Jin. Stress Analysis and Experimental Proof of Reducer under Internal Pressure[J].China Mechanical Engineering, 2007,18(3):365-369.)

[4] 陈孙艺.异径管应力分析及极限载荷的研究[D].上海:华东理工大学，2006.

(CHEN Sun-yi. Analysis and Study for Stress and Limited Load of Reducer [D]. Shanghai: East China University of Science and Technology, 2006.)

[5] 陶春达，李强.内压作用下异径弯管的应力分析[J].应用数学和力学, 2014，35(S1):50-54.

(TAO Chun-da, LI Qiang. Stress Analysis on Reducing Bend under Internal Pressure[J].Applied Mathematics and Mechanics，2014，35(S1):50-54.)

[6] 陶春达，李宗涛，吴明.内压作用下偏心异径管的应力分析[J].石油机械,2012,40(7):89-92.

(TAO Chun-da，LI Zong-tao，WU Ming. Stress Analysis of the Eccentric Reducing Pipe under the Effect of Internal Pressure[J].China Petroleum Machinery，2012，40(7):89-92.)

[7] 陈国理.压力容器及化工设备(上册)[M].广州：华南理工大学出版社，1988.

(CHEN Guo-li. Pressure Vessel and Chemical Equipment (Volume one) [M]. Guangzhou: South China University of Science and Technology, 1988.)

[8] 化工设备设计编辑委员会.超高压容器设计[M].上海：上海科学技术出版社，1983.

(Chemical Equipment Design Editorial Board. Design of Super High Pressure Vessel[M].Shanghai：Shanghai Science and Technology Publishing House，1983.)

[9] 赵国珍，战人瑞，陶春达，等.超高压设备的自增强方法——爆轰自增强[J].石油机械，1991，19(9)：1-9.

(ZHAO Guo-zhen, ZHAN Ren-rui ,TAO Chun-da, et al. Explosive Autofrettage for Extra-High-Tension Units[J]. China Petroleum Machinery，1991，19(9):1-9.)

[10] 战人瑞，陶春达，韩林,等.爆炸自紧残余应力及对构件疲劳强度的影响[J].爆炸与冲击，2005，25(3)：239-243.

(ZHAN Ren-rui ，TAO Chun-da，HAN Lin，et al. Influence on the Fatigue Strength with Residual Stress Induced by Explosive Autofrettage[J]. Explosion and Shock Waves，2005，25(3)：239-243.)

[11] 陶春达，战人瑞，韩林.100 MPa自增强压裂泵阀箱疲劳强度分析[J].机械强度，2005，27(1)：104-107.

(TAO Chun-da，ZHAN Ren-rui，HAN Lin. Research on Fatigue Strength of 100 MPa Autofrettaged Fluid Pump End [J]. Journal of Mechanical Strength，2005，27(1):104-107.)

[12] 战人瑞，陶春达，赵国珍，等.爆轰自增强弹塑性动力分析[J].西南石油学院学报，1999，21(4):82-85.

(ZHAN Ren-rui，TAO Chun-da， ZHAO Guo-zhen，et al. Elasto-plas Dynamic Analysis of Explosive Autofrettge[J].Journal of Southwest Petroleum Institute, 1999，21(4):82-85.)

[13] 战人瑞，陶春达.自增强设备最佳超应变度研究[J].石油学报，1996，17(4):128-136.

(ZHAN Ren-rui，TAO Chun-da. Study on Optimum Overstrain Extent of Autofrettaged Thick-walled Cylinder[J]. Acta Petrolei Sinica，1996，17(4):128-136.)

[14] 陶春达，战人瑞，赵国珍.高压注水泵泵头体最佳超应变研究[J].石油机械，1997, 25(1):15-18.

(TAO Chun-da, ZHAN Ren-rui，ZHAO Guo-zhen. Optimum Overstrain Extent Hydraulic End of High Pressure Water Flood Pump [J]. China Petroleum Machinery, 1997, 25(1):15-18.)

[15] 邓夕胜，陶春达.自增强超高压弯管最佳超应变研究[J].石油机械，2009，37(8):45-47.

(DENG Xi-sheng, TAO Chun-da. Study on the Optimum Overstrains Extent of Extra-high Pressure Elbow [J]. China Petroleum Machinery, 2009，37(8):45-47.)

[16] 战人瑞，陶春达，韩林，等.内壁带缺口的设备自增强超应变研究[J].石油化工设备，1996，25(3):7-12.

(ZHAN Ren-rui ,TAO Chun-da, HAN Lin,et al. Investigation in Optimum-overstrain of Autofrettaged Equipment with a Notch[J]. Petro-chemical Equipment，1996，25(3):7-12.)

[17] 战人瑞，陶春达，吕瑞典.自增强容器最佳超应变数值分析[J].石油化工设备，2003，32(6)：23-26.

(ZHAN Ren-rui，TAO Chun-da，LU Rui-dian. Numerical Analysis of Autofrettaged Vessel for Optimum Overstrain Extent[J]. Petro-chemical Equipment，2003，32(6)：23-26.)

(许编)

StudyonOptimumOverstrainExtentofAutofrettagedConcentricReducer

TAOChun-da1,ZHONGYun-long2

(1.School of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, China; 2. People′s Government of Muchuan Country Gaosun Township, Leshan 614504, China)

The mechanical model of concentric reducer was established based on axial symmetry, the stress of concentric reducer under 32.0 MPa internal pressure was calculated, and the characteristics of concentric reducer were discussed about the radial, axial, circumferential, and equivalent stress, the distribution rule of stress and the dangerous point were obtained. The optimum overstrain extent of autofrettaged concentric reducer was researched based on static strength, and the optimal autofrettaged pressure was obtained. For concentric reducer such as R(C)-100×50-Sch80S, the optimal autofrettaged pressure is 64.3 MPa, the optimum overstrain extent at dangerous point is 73.08%.

reducer; stress; finite element computation; overstrain extent; autofrettage

TQ050.2； TE969

A

10.3969/j.issn.1000-7466.2017.04.002

1000-7466(2017)04-0007-04①

2017-02-02

陶春达(1964-)，男(汉族)，四川渠县人，教授，主要从事工程力学教学与科研工作。