方法标准验证实验数据中离群值的识别

李玉武，任立军，闫 岩，殷惠民

国家环境分析测试中心，北京 100029

方法标准验证实验数据中离群值的识别

李玉武，任立军，闫 岩，殷惠民

国家环境分析测试中心，北京 100029

对方法标准验证实验中测量数据进行合格性审核，对于后续方法精密度计算是一个重要环节。文献中识别离群值的Grubbs法、Dixon法等经典方法有时不能满足要求。探讨了用稳健统计法识别离群值的可行性。基于2套文献数据和XRF方法标准验证实验精密度测量数据，对Grubbs法、Dixon法、Mandelh检验法、质控指标法和稳健统计法(四分位法、迭代法、合格数据范围判定法)进行了比较。结果表明：稳健统计法可有效识别离群值。但四分位法存在过度“检出”现象。综合考虑多种方法识别结果有利于提高离群值判定结论的可靠性。对于个别难以判断的情形，可借助质控指标、技术要求以及数据是否剔除对实验室间标准偏差的影响进行取舍。

方法标准验证；离群值识别；稳健统计法；X射线荧光光谱法

方法标准验证实验中，判断协作实验室精密度测量数据是否合格，对于后续方法精密度计算是一个重要环节。环境监测方法标准制修订技术导则[1]对此有明确要求，所有数据在进行数理统计处理之前均应通过合格性检查，以排除各种非随机因素的影响，增强数据统计分析结果的有效性和可靠性。实际工作中，从环境保护部官方网站上发布的标准编制说明附件“方法验证报告”中很难看到这一环节。大多数报告假定全部数据均合格，全部采用。有的报告中参与方法精密度计算的数据有缺失，但未见剔除离群值依据和说明[2-3]。

文献中常见的离群值识别方法有Grubbs法、Dixon法和Mandelh检验法[4-6]。有文献[7]指出，其中Grubbs法、Dixon法存在对离群值剔除不足的问题，不能满足标样协作定值对数据质控需求。Mandelh检验法是标准[4]推荐的协作实验室数据一致性检验方法。四分位法和稳健统计-迭代法在实验室检测能力验证数据处理中已有广泛应用[8-12]，但用于多家实验室方法标准验证实验数据中离群值处理，文献中鲜见报导。

研究基于2套文献数据和10家实验室对环境空气颗粒物中无机元素测定波长色散(WD-XRF)和能量色散X射线荧光光谱法(ED-XRF)标准验证实验中的精密度测量数据，探讨了用稳健统计法识别离群值的可行性。比较了多种识别离群值的方法结果。结合分析化学专业经验，提出了离群值剔除原则。

1 计算方法

1.1Mandelh检验法[4]

Mandelh统计量，常用于方法标准验证多家实验室数据一致性检验。h统计量计算公式为

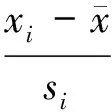
(1)

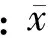
查表[4]可得Mandelh检验临界值：当α=0.01，实验室个数(L)分别为5、6、7、8、9、10时，h临界值等于1.72、1.87、1.98、2.08、2.13、2.18。当α=0.05，L分别为5、6、7、8、9、10时，h临界值等于1.57、1.66、1.71、1.75、1.78、1.80。临界值与重复测定次数无关。将hi与临界值比较，如果h统计量大于h临界值，95%则判为可疑值，如果h统计量大于h临界值，99%则判为离群值。可疑值也可称之为在95%置信水平下的离群值。

1.2四分位法[8]

将参与检验的数据从小到大排列：x1，x2，…，xn。中位值是一组数据的中间值，即有一半的结果高于它，一半的结果低于它。四分位法的稳健标准偏差用标准化IQR表示，它是结果变异性的量度，等于四分位间距(IQR)乘以因子0.741 3，与正态分布的标准偏差相类似。中位值和标准化IQR可以用Excel®的公式(2)方便求得：Q1=PERCENTILE(x1:xn, 0.25);Q3=PERCENTILE(x1:xn, 0.75);NIQR=0.7413×(Q3-Q1); 中位值=PERCENTILE(x1:xn, 0.50)，其中(x1:xn)表示数据组，n表示数据个数。

根据中位值和标准化IQR计算统计量(Z)：

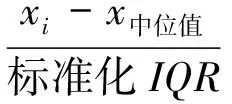
(2)

式中：如果Z≤2为正常值，Z>2为可疑值，Z≥3则为离群值。

1.3稳健统计-迭代法[9,13-14]

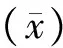
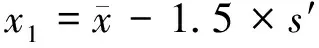
(3)

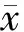
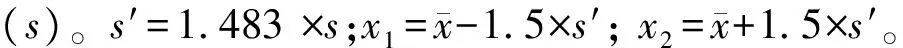
取得稳健平均值和稳健标准偏差后，数据可疑值和离群值的识别方法同四分位法。

1.4合格数据范围评定法

1.5质控指标法[7]

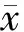
1.6经验模型法[15]

通过经验模型公式计算再现性标准偏差：sR=0.080×x0.85，x取各家实验室测定结果的中位值。然后计算Z比分数。如果Z≤2为正常值，Z>2为可疑值，Z≥3则为离群值。此经验模型适用范围是固体样品(如土壤、沉积物等)。

2 实验部分

XRF测量数据源于10家实验室对环境空气颗粒物中无机元素用WD-XRF和ED-XRF测定进行的方法标准验证实验，符合标准制修订技术导则[1]要求。

2.1颗粒物实际样品

参与方法验证协作实验的样品1#、5#、13#、2#、9#、14#均为环境空气颗粒物样品，H6#、154#为无组织排放颗粒物样品。元素Si基于采集在聚丙烯滤膜(2#、9#、14#)的环境空气PM2.5样品测试数据，其他元素为石英滤膜(1#、5#、13#、H6#、154#)上的TSP样品测试数据。原始测量数据见文献[3]。

2.2分析方法

取相同颗粒物样品由协作实验室分别用WD-XRF或ED-XRF测量。校准样品统一采用美国某公司提供的薄膜标样[3]。各家实验室根据仪器厂商提供的数据库选择最佳工作条件。测试步骤和测量条件示例见文献[3]。

2.3分析仪器

方法验证协作实验室涉及下列公司及仪器型号。WD-XRF:布鲁克(北京)科技有限公司 S4、S8；帕纳科公司Axios；岛津公司1800；理学公司RIX 3000。ED-XRF：天瑞公司EHM X100；帕纳科公司 E3、E5；岛津公司8000。

3 结果与讨论

3.1稳健统计法与经典方法概述及结果比较

文献中常见的识别离群值的经典方法有Grubbs法、Dixon法和Mandelh检验法。其中协作实验室方法标准验证实验数据的处理，文献[3]推荐采用数值法(Grubbs法)和作图法(Mandelh检验法)。计算中发现，Grubbs法和Mandelh检验法的计算公式完全相同。其区别是Grubbs法仅对参与检验的数据系列中最小或最大值进行检验，而Mandelh检验法同时对所有数据进行h统计量计算，不需要对数据按大小进行排列。比较2种方法临界值发现(表1)，Grubbs法与Mandelh法相比，对离群值的判断依据更宽松。

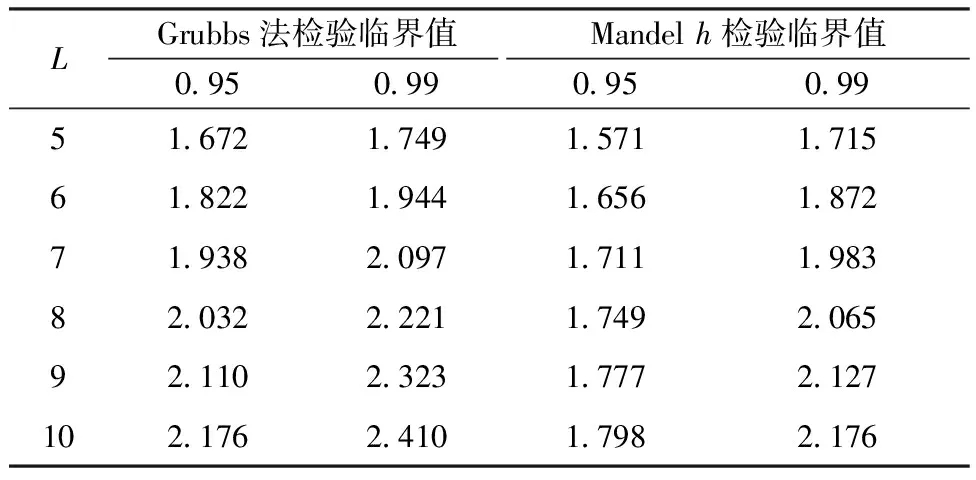
表1 Grubbs法检验[5]与Mandel h法检验临界值[4]比较Table 1 Critical values comparison betweenGrubbs and Mandel h test

四分位法和迭代法均属于稳健统计法，在实验室检测能力验证数据处理中已有广泛应用。这2种方法对于实验室检测能力是否合格的判断，就是基于对统一发放的样品上报结果合格值与异常值(包括可疑和离群值)的识别。由于这2种方法均属于稳健统计法，可疑值和离群值对统计参数(平均值和标准偏差)的计算过程没有影响，或影响较小，不像经典的Grubbs法和Mandelh检验法，平均值和标准偏差的计算要求包括异常值在内的所有数据。因此，四分位法和稳健统计-迭代法对异常值的识别更敏感。判别标准也很简单，根据Z比分数数值，就可将数据分为合格(Z≤2)，可疑(Z>2)和离群(Z≥3)。

表2是基于标准附录[4]离群值识别示例数据，3种稳健统计方法与经典方法的比较结果。标准附录[4]示例计算结果指出，3#样品中17.15，4#样品中19.23是离群值，5#样品中24.14是可疑值。对这3个数据，Mandelh检验法、Grubbs法和Dixon法、四分位法和稳健统计-迭代法、范围判定法均有相同或基本相同的结论。但四分位法、稳健统计-迭代法和范围判定法还识别出1#样品中4.42是可疑值，5#样品中17.57是离群值。结果表明，稳健统计法(四分位法、迭代法、范围判定法)比经典的Mandelh检验法、Grubbs法和Dixon法更容易发现异常值。异常值的检出率大小顺序为四分位法、迭代法、范围判定法>Mandelh检验法、Dixon法>Grubbs法，检出个数分别为5、5、5、4、4、2。

表2 木馏油热滴定数据[4]离群值识别经典方法与稳健统计法结果比较Table 2 Comparison between classical and robust statistical method to detectoutliers based on titration data of wood distillate

注：①Mandelh检验临界值为1.78(α=0.05，L=9), 2.13(α=0.01，L=9)；②Dixon检验临界值为0.512(α=0.05，L=9)，0.635(α=0.01，L=9)；③Grubbs检验临界值为2.110(α=0.05，L=9)，2.323(α=0.01，L=9)；④统计结果一列中“范围判定法”给出测量数据正常值范围;异常值字体加粗处理，可疑值右上角标注“*”，离群值右上角标注“**”；“—”表示无相应值。

3.2稳健统计法与质控指标法结果比较

标准样品协作定值、方法标准验证实验对数据质量要求较高时，经典的Grubbs法和Dixon法识别离群值能力有时不能满足需要。文献[7]在黄金标准样品定值实验数据处理中，参考日常质控指标提出了相对偏差允许限为依据的离群值统计识别方法(以下简称质控指标法)。离群值剔除是否合理用剔除离群值后数据的平均值与黄金标准样品的标称值之间的误差大小来衡量。据文献作者介绍，采用此方法后数据质量分数等级有了明显提高，增强了数据统计分析的有效性。表3列出了文献[7]全部15个样品，每个样品10个独立实验室上报的共计150个测量数据中的离群值6种方法的识别过程统计量及结果(全部原始测量数据见文献[7])。所有这些离群值用Grubbs法和Dixon法识别，均无检出[7]。

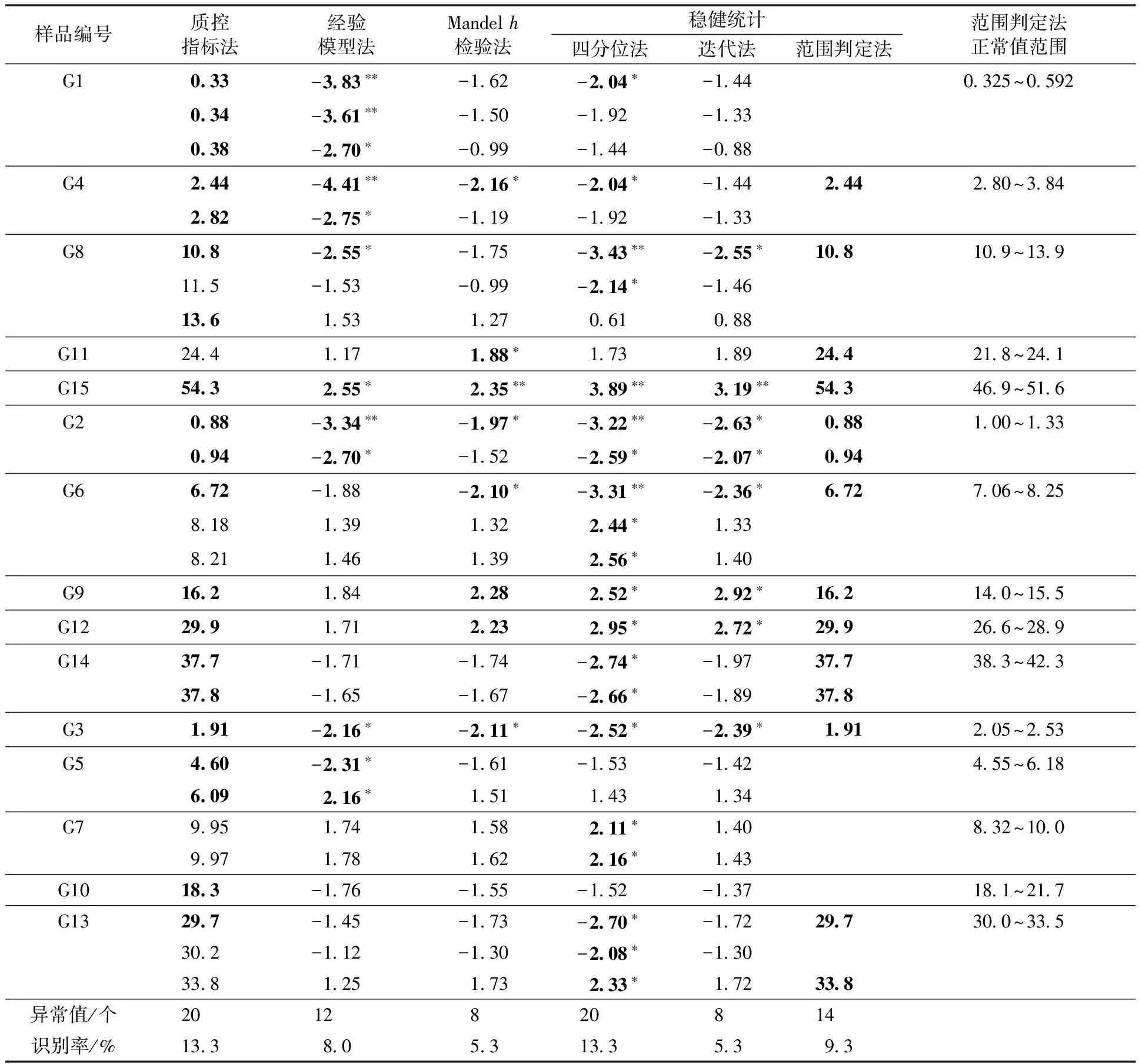
表3 基于文献[7]数据离群值识别多种方法结果比较Table 3 Comparison of different method to detect outliers based on literature data[7]

注：异常值字体加粗处理，可疑值右上角标注“*”，离群值右上角标注“**”。

从表3可见，离群值的检出个数大小顺序为四分位法(20)、质控指标法(20)>范围判定法(14)>经验模型法(12)>Mandelh检验法(8)>迭代法(8)。括号内的数字是已识别异常值的个数。除了文献[7]方法识别了20个异常值外，还有8个异常值分别被其他方法识别。从异常值识别率来看，6种方法大致可以分为3类：四分位法、质控指标法为第1类；范围判定法、经验模型法为第2类；Mandelh检验法和迭代法为第3类。全部可疑值和离群值被不同方法累计识别次数统计见图1。从图1可以看出，28个测定结果中，被2种以上方法识别的有20个，3种以上方法识别的有13个，4种以上方法识别的有9个。显然，同时被几种方法检出的，其结果可靠性更高。

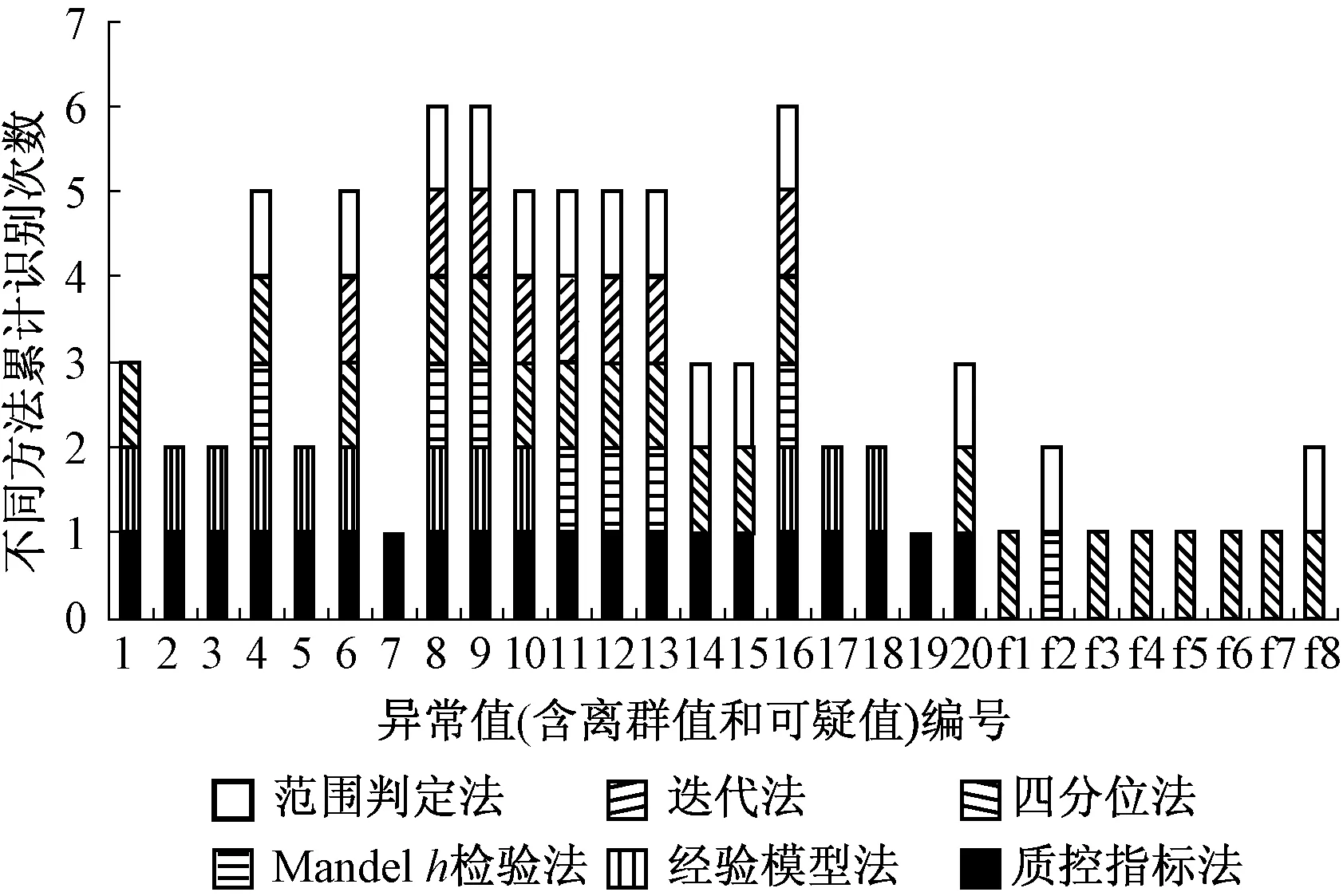
图1 不同方法对异常值(含离群值和可疑值) 识别累计次数统计图Fig.1 Cumulative count diagram of differentmethod to detect outliers

文献[7]指出，根据判别依据，20个异常值中，有17个被准确识别，有3个属于过度剔除。由此推断，四分位法肯定也存在过度剔除情况。Mandelh检验法和迭代法识别结果偏低。基于四分位法处理实验室检测能力数据经验，当各家实验室提交的数据离散程度较低时，有可能出现个别实验室的数据从技术要求角度评判是合格的，而依据Z比分数却被判为离群值的情况；反之，当数据的离散程度较大时，有可能出现虽然某实验室数据从技术要求角度评判是不合格的，但依据Z比分数却被判为合格结果的情况。合格数据范围判定法识别率合适，值得关注。

经验模型法从原理上讲与质控指标法一样。不同点是前者适用于所有固体样品，而后者是总结黄金样品测试结果而得，针对性更强。从识别离群值结果看，质控指标法对数据质量的要求更严格。

3.3用稳健统计法识别XRF方法标准验证实验数据中的离群值

文献研究结果表明，质控指标法是识别离群值的一条有效途径。但对于方法标准验证数据处理，如果缺乏长期积累的用于判断数据质量的质控指标模型，很难应用质控指标法。3.2节比较结果表明，稳健统计法可以有效识别离群值，得到与质控指标法基本相符的结果。

用3种稳健统计法(四分位法、迭代法和范围判定法)对XRF方法标准验证实验精密度测量数据进行合格性审核并与经典的Grubbs法、Dixon法、Mandelh检验法进行了比较。精密度测量数据中选择了大于等于定量限(4倍方法检出限)的样品元素测定数据(以下简称有效测量数据)。考虑到篇幅所限，表4列出了每个元素5个样品测定数据(3个环境样品、2个无组织排放样品，Si仅涉及3个环境样品)各方法识别离群值、可疑值或异常值。检出率统计数据包括了可疑值和离群值(2种置信水平和Z>2、Z≥3的情况)。不同方法检出率和数据采用率见表4最后2行。各元素测量数据采用率(保留数据与有效测量数据之比)列入表4最后1列。

表4 XRF方法精密度测量数据不同方法离群值识别结果比较Table 4 Comparison of different method to detect outliers in XRF precision measurement data

从表4可以看出，多种方法对异常值的识别率顺序为四分位法(14.2%)>范围判定法(11.9%)>迭代法(9.0%)>Mandelh检验法(7.0%)>Dixon法(5.3%)>Grubbs法(4.0%)。此例再次证实，对于标准定值和方法标准验证实验数据，由于对数据质量要求较高，经典的Grubbs法、Dixon法对离群值检出率较低，不能满足需要。Mandelh检验法检出率虽有改善，但仍不能满足要求。四分位法对离群值(和可疑值)很敏感，有时有“过度”检出之嫌。其结果需要和其他方法结果一起考虑。范围判定法结果较合理，是最终决定是否剔除离群值的主要依据。综合判断后得到的数据采用率(89.0%)在迭代法(91.0%)和范围判定法(88.1%)之间。

表5是从表4数据中选出的离群值4种方法判断示例。显示了不同方法识别离群值过程的统计量。各示例简要说明如下：

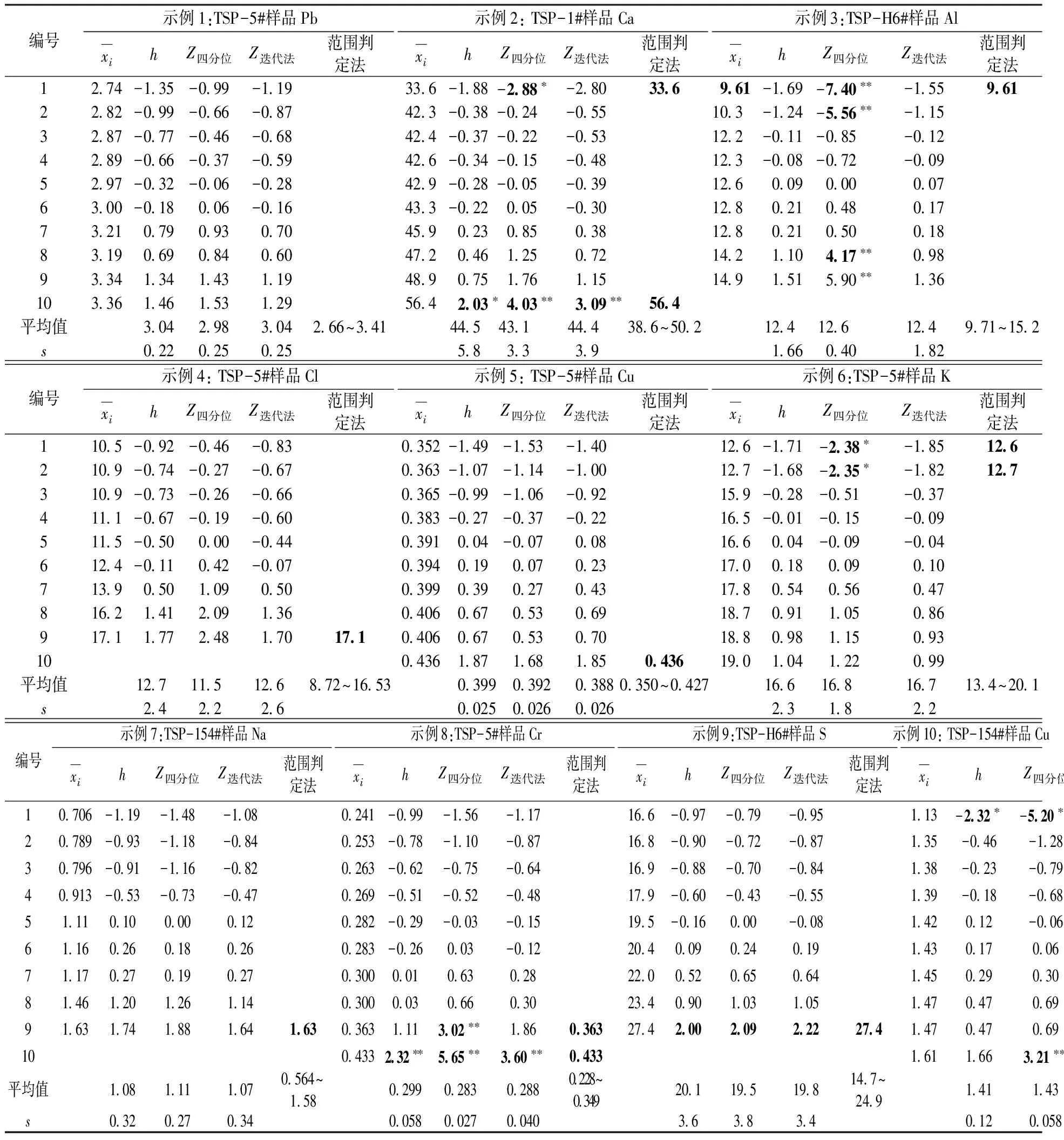
表5 4种方法识别离群值示例Table 5 Examples for detection of outliers in XRF precision measurement data based on four methods

注：Mandelh检验临界值为1.80(α=0.05，L=10), 2.18(α=0.01，L=10)；1.78(α=0.05，L=9), 2.13(α=0.01，L=9)；异常值字体加粗处理，可疑值右上角标注“*”，离群值右上角标注“** ”。

示例1：4种方法结果完全一致。其特点是不同方法统计量距离临界值较远。不存在离群值。

示例2：存在2个异常值，与正常值距离较远。这2个数据Mandelh检验法均判断为可疑值；四分位法和迭代法判断结果为1个可疑值，1个离群值；范围判定法结果是这2个数据均为离群值；综合判断结果为2个数据均剔除。

示例3：Mandelh检验法与迭代法结果基本一致，未检出。范围判定法检出1个，四分位法判断有4个离群值。其原因是正常数据中中位值附近数据精密度较好。 四分位法结果为过度检出。综合判断结果：采用范围判定法结果，剔除9.61这个数据。

示例4：Mandelh检验法判断均为合格数据，但其中有1个数据在临界值附近。四分位法判断存在有2个可疑值，迭代法与Mandelh检验法一致。范围判定法有1个异常值，另外1个值也在边界附近。结合分析测试技术要求及实验室间标准偏差判断，这2个数据均删去。

示例5：数据0.436被Mandelh检验法判断为可疑值，略微超出了范围判定法划定的范围，但其他3种方法均判断为正常值。其原因是数据精密度较好，各家实验室测量数据均在中位值附近。结合技术要求及删去此数据后对实验室间标准偏差结果影响，综合结论为保留。这个例子表明，Mandelh检验法识别的离群值结果不一定准确，也存在偏严的现象。

示例6：Mandelh检验法和迭代法判别结果基本一致，但均在临界值附近。同样的2个数据四分位法和范围判定法判断为可疑值和异常值。综合结论为删去这2个数据。

示例7：Mandelh检验法、四分位法和迭代法对数据1.63判断结果基本一致，均为合格，但均在临界值附近。其原因是此系列数据离散度较大。范围判定法结果为离群值。综合结论：剔除。

示例8：4种方法均判断数据0.433为离群值。0.363被四分位法和范围判定法判为离群值。综合判定结果：剔除0.433和0.363。

示例9：4种方法均判断数据27.4为离群值。综合结论为剔除。此种情况判定结论可靠性高。

示例10：4种方法均判断数据1.13为离群值，而对于1.61，Mandelh检验法判断为正常，但位于临界值附近。其他3种方法均判断为离群值。综合结论为这2个数据均剔除。

上述10个示例可归纳为3种情况：① 4种方法一致判定为合格值(如示例1)； ② 4种方法一致判定为离群值(如示例2、8、9)；③ 4种方法判定结果不一致，此种情况数据有3个特征：第一，可疑数据在一些判别方法的临界值附近(如示例4、6、10)；第二，数据波动较小(如示例3、5)，四分法和Mandelh检验法易产生过度“检出”的误判；第三，数据波动较大(如示例7)。

综合上述示例可以总结出下列基本原则：①不同方法判别结论一致时，其结果可靠性高；②四分位法有过度“检出”的风险；③几种方法识别结论不一致时，合格数据范围判定法是主要参考依据；④对于个别难以判断的情形，可借助实验室日常质控指标、技术要求以及数据剔除是否对实验室间标准偏差产生影响进行取舍。

4 结论

识别离群值的经典方法(如Grubbs法、Dixon法等)有时不能满足方法标准验证实验数据合格性审查要求。合格数据范围判定法可有效识别方法精密度测量数据中的离群值。其结果可以作为综合判断结果的重要参考依据。四分位法也可以用于识别离群值，但有时存在“过度”识别现象。综合考虑多种方法识别结果有利于提高离群值判定结论的可靠性。对于个别难以判断的情形，可借助质控指标、技术要求和数据剔除是否对实验室间标准偏差产生影响进行取舍。

致谢：XRF方法标准验证实验得到下列实验室的大力支持：湖南省环境监测中心、北京市环境保护监测中心、中科院地球环境研究所、上海市环境科学研究院、天津市环境监测中心、环保部标准样品研究所、江苏天瑞仪器股份有限公司、布鲁克(北京)科技有限公司、上海思百吉仪器系统有限公司(帕纳科业务部)和岛津企业管理(中国)有限公司上海分公司，在此一并表示感谢。

[1] 环境保护部科技标准司. 环境监测-分析方法标准制修订技术导则: HJ 168—2010 [S]. 北京：中国环境科学出版社，2012.

[2] 环境保护部科技标准司. 空气和废气-颗粒物中金属元素的测定-电感耦合等离子体发射光谱法编制说明 [EB/OL]. (2015-03-05) [2016-04-07].http://www.mep.gov.cn/gkml/hbb/bgth/201503/W020150305644878339248.pdf.

[3] 国家环境分析测试中心.《环境空气-无机元素的测定-X射线荧光光谱法》(征求意见稿)编制说明[EB/OL]. (2016-03-22) [2016-07-15].http://www.zhb.gov.cn/gkml/hbb/bgth/201603/W02016032237 4754088793.pdf.

[4] 全国统计方法应用标准化技术委员会. 测量方法与结果的准确度(正确度与精密度)第2部分：确定标准测量方法重复性与再现性的基本方法：GB/T 6379.2—2004 [S].北京：中国标准出版社，2009.

[5] 全国统计方法应用标准化技术委员会. 数据的统计处理和解释-正态样本离群值的判断和处理：GB/T 4883—2008[S].北京：中国标准出版社，2008.

[6] 全国统计方法应用标准化技术委员会. 利用实验室间比对进行能力验证的统计方法: GB/T 28043—2011 [S].北京：中国标准出版社，2011.

[7] 杨理勤，穆新华，郑振云. 常量金标准物质定值中离群值的统计识别[J].岩矿测试，2013，32(3)：483-486.

YANG Liqin, MU Xinhua, ZHANG Zhenyun. Statistical identification of outliers in ore gold refenrence material to determine the optimal value [J]. Rock and Mineral Analysis，2013，32(3)：483-486.

[8] 中国合格评定国家认可委员会. 能力验证结果的统计处理和能力评价指南: CNAS-GL02[EB/OL].(2014-09-15)[2016-09-28].https://www.cnas.org.cn/images/rkgf/sysrk/rkzn/2015/06/04/2E558652D DEE55F50EDEE49E64499797.pdf.

[9] 中国合格评定国家认可委员会. CNAS T0476低合金钢中化学成分分析能力验证计划结果报告：附录D[R].北京：中国合格评定国家认可委员会，2010.

[10] 邢小茹，马小爽，田文，等. 实验室间比对能力验证中的两种稳健统计技术探讨[J].中国环境监测，2011，27(4)：4-8.

XING Xiaoru， MA Xiaoshuang， TIAN Wen，et al.Two robust statistic techniques in proficiency testing by interlaboratory comparisons[J].Environmental Monitoring in China，2011，27(4)：4-8.

[11] 吴忠祥.实验室能力验证中的分割水平检测样品与稳健统计技术[J].中国环境监测，2003，19(4)：8-10.

WU Zhongxiang.Split-level test sample and robust statistical techniques in laboratory proficiency testing[J].Environmental Monitoring in China，2003，19(4)：8-10.

[12] 滕曼，付强，吴晓凤，等. 环境监测实验室水中砷、汞监测能力考核结果评价[J].中国环境监测，2014，30(4)：183-187.

TENG Man， FU Qiang，WU Xiaofeng， et al.Results analysis of proficiency assessment of As and Hg monitoring in ground water[J].Environmental Monitoring in China，2014，30(4)：183-187.

[13] 狄一安，孙海容，李玉武，等. 用质控图和稳健统计迭代法评估环境检测实验室测量不确定度[J].岩矿测试，2014，33(1)：57-66.

DI Yi’an, SUN Hairong,LI Yuwu, et al. Evaluation of measurement uncertainty in environmental test laboratory by quality assurance and control charting and robust statistics [J].Rock and Mineral Analysis, 2014，33(1)：57-66.

[14] Analytical Methods Committee. Robust statistics: A method of coping with outliers[R]. London：Royal Society of Chemistry(ISSN 1757-5958),2001.

[15] 李玉武，狄一安，孙海容，等. 用经验模型评估环境样品测量不确定度[J].中国无机分析化学，2012，2(1)：1-6.

LI Yuwu, DI Yi’an, SUN Hairong,et al.Study on evaluation of measurement uncertainty of environmental sample by empirical model[J].Chinese Journal Inorganic Analytical Chemistry，2012，2(1)：1-6.

StudyonDetectionofOutliersinInter-LaboratoryCollaborationExperimentalDataforValidationofAnalysisMethodStandard

LI Yuwu,REN Lijun,YAN Yan,YIN Huimin

National Research Centre for Environmental Analysis and Measurements,Beijing 100029,China

It is an important for the calculation of the analysis method precision index to check the measurement data in inter-laboratory collaboration experiment. The Grubbs method and Dixon method, which are used to identify the outliers, can not meet the requirements sometimes. It is proposed to detect outliers by robust statistical method.The results of several methods to detect outliers based on two literature data and XRF precisions experimental data from inter-laboratory collaboration are compared. It is shown that the qualified data range judgment method based on robust statistical method can effectively identify outliers.Quartile method sometimes exists “excessive” identification phenomenon.The reliability of the conclusion can be improved by considering the results of several methods at same time.For some difficult situation in judgment, it is effective ways with the help of quality control indicators, technical requirements and whether the data deleted the impact on standard deviation between the laboratories.

collaboration experiment for analysis method validation;detection of outliers;robust statistical method;X-ray Fluorescence Spectroscopy(XRF)

X830.3

A

1002-6002(2017)05- 0167- 09

10.19316/j.issn.1002-6002.2017.05.24

2016-09-28；

2016-12-05

国家重大科学仪器设备开发专项(2014YQ060773，2011YQ170065)

李玉武(1956-)，男，湖北武汉人，博士，研究员。

殷惠民