基于IDA-MC方法的公路边坡震害风险概率评价

于 伟，折学森

(1. 长安大学公路学院，陕西 西安 710064；2. 长安大学特殊地区公路工程教育部重点实验室，陕西 西安 710064)

基于IDA-MC方法的公路边坡震害风险概率评价

于 伟1,2，折学森1,2

(1. 长安大学公路学院，陕西 西安 710064；2. 长安大学特殊地区公路工程教育部重点实验室，陕西 西安 710064)

为提高公路边坡抗震能力，本文开展了公路边坡震害风险概率评价研究。选取210国道K359+440处公路边坡为研究对象，采用增量动力分析方法研究了边坡震害易损性，绘制了边坡震害易损性曲线并得到了边坡在一定地震动峰值加速度作用下超越(发生)某等级震害的概率；在边坡所在场地地震动分布特征研究的基础上，采用蒙特卡罗方法计算了边坡未来50年内超越(发生)各等级震害的风险概率。研究结果表明：当地震动峰值加速度达到0.7 g时，边坡超越严重损伤的概率为53.188%，达到0.8 g时，边坡超越严重损伤的概率高达99.086%；未来50年内边坡超越严重损伤的风险概率为29.07%，发生毁坏的风险概率为7.62%。

公路边坡；地震灾害；增量动力分析；易损性；蒙特卡罗方法；风险概率评价

0 引言

边坡是公路最常见的结构物之一，在唐山地震、汶川地震等破坏性地震中，公路边坡滑塌、开裂和防护设施损坏等震害十分普遍，在极震区，大规模滑坡、崩塌和泥石流等严重震害也时有发生，由此造成的道路中断经常成为陆路救援的“死结”[1]，因此，研究公路边坡在地震作用下的破坏机理和损伤程度对提高公路抗震能力和区域防灾减灾能力具有重要意义[2]。

在地震作用下，某一公路边坡的震害程度取决于两方面，一是边坡本身的抗震性能，属于边坡震害易损性评价的内容；二是公路边坡所在场地遭遇地震的强度和可能性大小，属于地震危险性评价的内容[3]。公路边坡震害风险概率评价以边坡震害易损性评价和地震危险性评价为基础并分析两者的耦合特征，其评价结果以某一特定边坡在未来一定时间内超越(发生)各等级震害的概率表征[4]。

国内外学者对结构的震害风险评价进行了大量研究。徐光兴等[5]分析了地震作用下边坡动力响应规律以及地震动参数对边坡动力响应的影响。Yoshihisa等[6]采用经验方法开展了多条高速公路路堤的震害易损性评价。Luisa等[7]分析了某钢筋混凝土结构震害易损性的时变特征。谷音等[8]基于Monte Carlo方法计算了典型矮塔斜拉桥各震害等级的风险概率。吕大刚[9]分析了本质不确定性和知识不确定性对结构震害风险评价结果的影响并推导了有关公式。贾兴利等[10]研究了公路边坡在地震动荷载作用下永久动力位移的响应规律。陈鲲等[11]采用风险积分法耦合了结构倒塌能力的不确定性。Melani等[12]绘制了低层钢筋混凝土框架结构震害易损性曲线并进行了震害经济损失评估。

通过已有研究可知，虽然公路边坡震害十分严重，但系统性的边坡震害易损性、地震危险性和风险概率评价还鲜有报道；另一方面，我国公路抗震遵循“小震不坏、中震可修、大震不倒”的设计原则[13]。这一原则初步体现了基于性能的抗震设计思想，但其地震强度指标和地震损伤指标缺乏明确定义，在实际应用中受到了很大限制。而公路边坡震害风险概率评价是定量研究边坡抗震可靠性的有力工具，在指导公路抗震设计中具有独特优势。鉴于此，本文以210国道K359+440边坡为例进行震害易损性、地震危险性和风险概率评价研究，为提高公路抗震能力提供理论基础。

1 公路边坡震害易损性评价

震害易损性评价最早是从核电站和大坝等结构开始的，并通过易损性曲线或易损性矩阵的形式体现评价结果[14]。

1.1理论性震害易损性评价

震害易损性评价主要有经验法和理论法两种。理论性震害易损性评价采用理论方法反应结构某特定损伤程度与地震动强度的概率关系。理论性震害易损性评价的优点有[6]：

(1)易于控制加载水平

理论性震害易损性评价采用计算机人工加载，可以选择不同强度和不同振型的地震动记录，不但可以充分体现结构所在场地遭受地震动的不确定性，还可以减小主观因素对评价结果的影响。

(2)实现对震害损伤参数的定量控制和研究

在理论性震害易损性评价中，震害状况通过软件自动输出，避免了人工震害调查确定结构损伤状况的误差，从而实现对震害损伤的定量控制和研究。

(3)实现对单体结构的精确研究

理论性震害易损性评价通过建立有限差分模型进行仿真，能够充分体现不同结构抗震性能的差异，实现对单体结构的精确研究。

本文采用理论方法进行公路边坡震害易损性评价，主要内容包括：公路边坡震害损伤判别、边坡结构形式确定、地震动输入确定、增量动力分析、概率性地震需求分析(PSDA)和易损性曲线的绘制等。

1.2公路边坡震害损伤判别

公路边坡震害损伤判别是进行边坡震害易损性评价的基础和前提，应从定性和定量两方面进行，即划分边坡震害等级和选取边坡震害损伤参数。

中国《生命线工程地震破坏等级划分(GB/T 24336—2009)》和美国HAZUS99将公路和桥梁震害进行了5级划分[15-16]。本文参照上述划分方法和公路边坡震害的特点，将公路边坡震害分为基本完好、轻微损伤、中等损伤、严重损伤和毁坏5级。

由于公路边坡顶面对地震动的放大作用最为强烈，本文基于位移破坏准则选取边坡顶面横向最大永久位移dmax作为震害损伤参数。作者于2008年6月调查了汶川地震震区的149处受损公路边坡，调查区域的地震烈度为Ⅶ～Ⅻ度。根据149处受损边坡的震害状况，总结了场地PGA与dmax的对应关系，见式1。

(1)

根据汶川地震的监测资料，震中映秀镇的PGA达到了0.977g，参照汶川地震公路边坡的整体受损状况，可以认为边坡在震中会发生最严重等级的震害，即毁坏；另一方面，由式1可知，当PGA=0.977g时，dmax达到了1.226%，即超过了1.2%，因此，将dmax=1.2%作为严重损伤与毁坏的界限是合理的。在此基础上，建立dmax与公路边坡震害等级的对应关系(表1)。

表1 公路边坡震害等级与震害损伤参数对应关系Table 1 Corresponding relationship between highway slopeseismic disaster levels and seismic damage parameter

1.3边坡结构形式和地震动输入确定

(1)边坡结构形式确定

本文选取210国道K359+440公路路堑边坡进行研究，根据我国第四代地震区划图，该边坡所在场地位于PGA的0.15g分区，即基本烈度Ⅶ度区。该边坡坡度1∶0.5，坡高14.5 m，边坡土体为Q4黄土(图1)。

在对该边坡建模时，对路基土和边坡土体选用弹塑性本构关系，屈服准则选取摩尔-库伦准则[17]。通过查阅210国道地勘资料和室内试验，确定了路基土和边坡填土的各项参数(表2)。

图1 210国道K359+440公路边坡基本形式

材料弹性模量/MPa泊松比体积模量/MPa剪切模量/MPa密度/(kg·m-3)粘聚力/kPa内摩擦角/(°)路基土48000345000179119700034003300边坡土体42000344375156716300031002800

(2)地震动输入确定

由于PGA直接与地震的惯性作用有关，即地震对公路边坡作用力的最大值为PGA与边坡质量之积，且PGA的测定可以避免烈度等其他指标测定中的主观因素，因此本文选取PGA作为地震动强度指标。

借鉴文献[18]的研究成果，论文选取美国太平洋地震工程研究中心(PEER)提供的一般中硬场地的15条地震动记录进行IDA分析，并将各地震动记录的PGA调整至0.2g、0.4g、0.6g、0.8g、1.0g和1.2g，持时调整至15.0 s，共计得到90条地震动记录。

1.4概率性地震需求分析

将各地震动记录输入已建立的公路边坡模型进行90次动力响应分析，分别记录各地震动对应的边坡顶面横向最大永久位移值dmax(图2)。

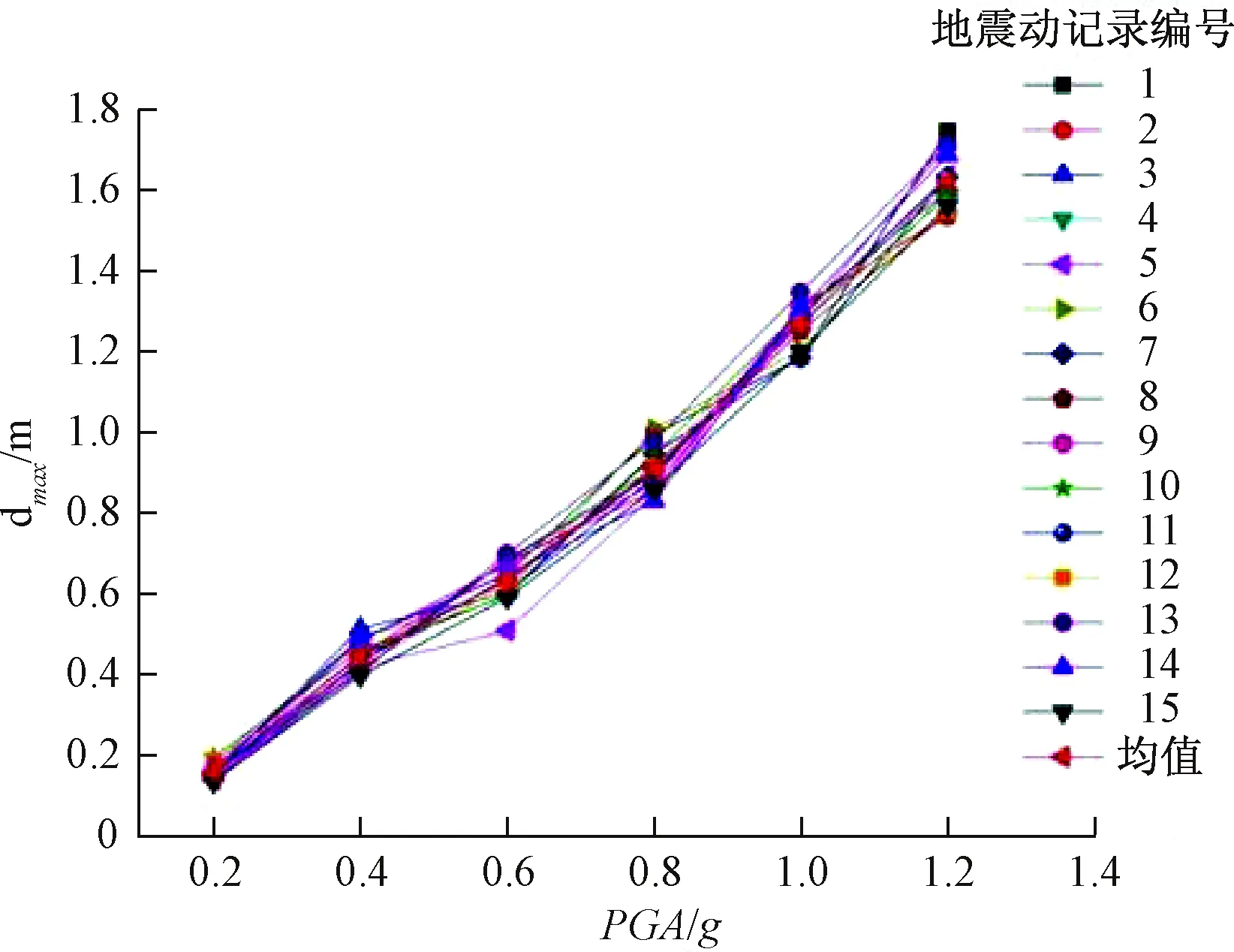
图2 公路边坡IDA分析结果

根据文献[19]，dmax均值与PGA的关系见式2。

(2)

式中：a、b——待估参数，根据边坡IDA分析结果对a、b进行回归，得：a=1.265 4、b=1.268 7。

则式2可改写为式3。

dmax=1.265 4PGA1.2687

(3)

边坡在地震作用下超越第j级震害的概率，即发生第j级或比第j级更严重震害的概率见式4。

(4)

式中：Pj——边坡在地震作用下超越第j级震害的概率；

Rj-——边坡发生第j级震害时对应的dmax取值下限(表1)；

S——地震造成的边坡震害损伤，即dmax的实际取值。

根据文献[20]，lnRj-和lnS均服从正态分布，因此式4可改写为式5。

(5)

式中：β——边坡震害损伤对地震动强度的离散程度。β采用式6计算。

(6)

式中：N——PGA取值数量，本文中N=6。结合IDA分析结果和式6，可计算得β=0.074 3，将不同PGA和Rj-代入式6可绘制边坡震害易损性曲线(图3)。

图3 边坡震害易损性曲线

由图3可知，PGA越大，边坡震害越严重，即边坡发生更严重等级震害的概率越大；当PGA达到0.7g时，边坡超越严重损伤的概率为53.188%，PGA达到0.8g时，边坡超越严重损伤的概率高达99.086%，即边坡几乎必然发生严重损伤和毁坏，可见该边坡的震害易损性较高。

2 公路边坡震害风险概率评价

2.1公路边坡震害风险概率计算方法

特定公路边坡的震害风险概率在数值上等于边坡所在场地地震危险性与边坡震害易损性的卷积，即未来t年内对边坡在所有地震事件作用下超越各等级震害概率的积分见式7。

(7)

式中：Pj,T=t——未来t年内边坡超越第j级震害的风险概率；

f(S)——风险事件对边坡综合效应的概率密度函数，即未来t年内dmax取值的概率密度函数。

f(S)的计算方法见式8。

f|S)=f|S|E)f(E)

(8)

式中：E——地震事件；

f(S|E)——给定E下dmax取值的条件概率密度，即边坡震害易损性评价结果。

f(E)为地震事件发生的概率密度函数，即场地地震动分布模型，是地震危险性评价结果。

结合式7和式8，可得边坡超越某等级震害的风险概率计算方法见式9。

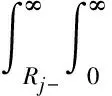
(9)

2.2场地地震动分布模型

场地地震动分布模型包括场地地震烈度概率分布模型和地震烈度与PGA的转换关系两方面。

(1)场地地震烈度概率分布模型

文献[21]对我国“三北”地区数十个场地的地震危险性评价结果进行了分析，结果表明，某一场地未来50年内的地震烈度服从极值Ⅲ型分布，其分布函数见式10。

(10)

式中：ω——最高烈度值，根据我国通用的烈度划分方法，ω=12；

ε——众值烈度，即未来50年内超越概率63%的烈度值；

K——形状参数。

确定形状参数有3种方法，即分位值法、最小二乘法和极大似然法，从拟合的角度看，最小二乘法最佳，但从工程实用的角度，取基本烈度，即未来50年内超越概率10%所对应的K值即可满足要求，论文采用后者计算K值。

由式10可得，未来任意t年内场地地震烈度的概率分布函数见式11。

(11)

对式11求导，可得未来t年内场地地震烈度的概率密度函数见式12。

(12)

(2)地震烈度与PGA的转换关系

本文采用世界地震工程之父——刘恢先提出的地震烈度与PGA的转换关系见式13。

PGA=10Ilg2-0.01

(13)

式中：I——地震烈度。

需要指出的是，虽然地震烈度取值是1～12的整数离散变量，但考虑到计算的精确性和模型的适用性，将式13中的地震烈度作为连续变量进行研究。

2.3基于Monte Carlo方法的公路边坡震害风险概率评价

结合式5、式9、式11和式12可知，若直接采用数值方法计算边坡震害风险概率，将不可避免的进行复杂的积分运算，且不能保证在积分域上实现收敛，鉴于此，论文采用Monte Carlo方法进行边坡震害风险概率评价。

(1)基本思想

根据Monte Carlo方法的基本思想，采用Matlab软件按式12对地震烈度进行n次抽样，并根据式13对地震烈度和PGA进行转换，则每单个PGA样本在整体样本中出现的概率为1/n。定义Pj(PGAi)为在PGAi作用下边坡超越第j级震害的概率，则当n足够大时，根据大数定理，式9可以转化为式14。

(14)

(2)实例分析

本文以210国道K359+440边坡为例进行未来50年内边坡震害风险概率评价。采用CPSHA方法评价该边坡所在场地的地震危险性，可得研究场地未来50年内一定超越概率水准的PGA，结合式13，可得相应的地震烈度值(表3)。

表3 研究场地一定概率水准的PGA与地震烈度值Table 3 PGA and seismic intensity of the research site

注：1gal=1 cm/s2

根据表3和式10，采用未来50年超越概率10%的地震烈度和未来50年超越概率63%的众值烈度对形状参数K进行待定，可得：

解得：K=8.397。则研究场地未来50年内的地震烈度概率分布函数见式15。

(15)

由式15可知，研究场地未来50年内的地震烈度概率分布见图4。

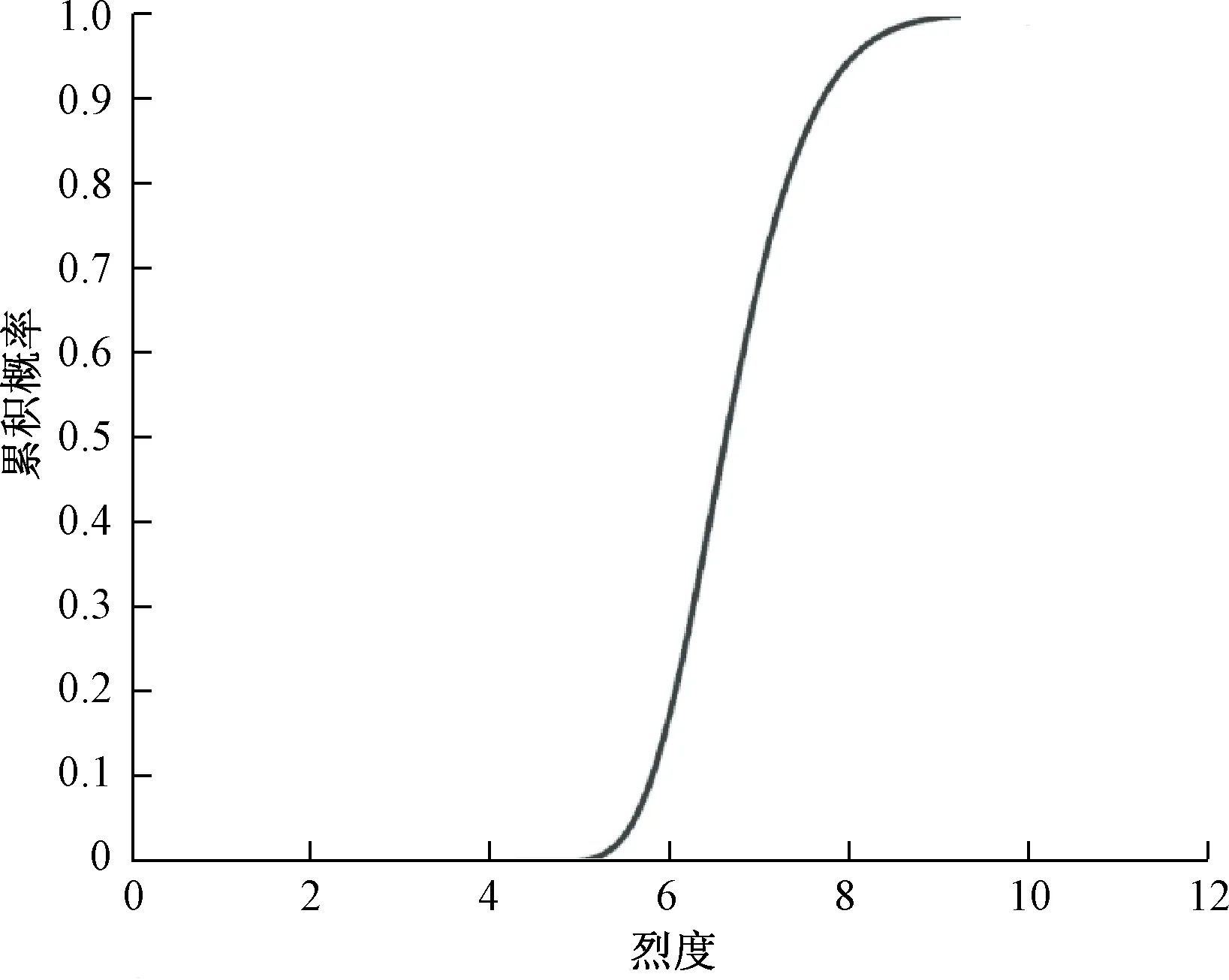
图4 研究场地未来50年内的地震烈度概率分布图

对式15求导，得到研究场地未来50年内地震烈度的概率密度函数见式16。

由式16可知，研究场地未来50年内的地震烈度概率密度函数见图5。

(16)

图5 研究场地未来50年内的地震烈度概率密度图

按照式16所示的研究场地地震烈度概率密度，采用Matlab软件根据Monte Carlo方法进行抽样，得到1 000个随机数I1、I2、I3、……、I1 000，这1 000个随机数表示研究场地未来50年内可能遭遇的1 000个地震烈度的可能，且这1 000个随机数符合场地地震危险性评价结果，即服从式16所示的概率分布函数。将I1、I2、I3、……、I1 000带入式14中，可得研究场地未来50年内可能遭遇的PGA1、PGA2、PGA3、……、PGA1 000。

根据图3，可得在PGA1、PGA2、PGA3、……、PGA1 000作用下，边坡超越轻微损伤的概率分别为P2(PGA1)、P2(PGA2)、P2(PGA3)、……、P2(PGA1 000)，则根据式14可得边坡未来50年内超越轻微损伤的风险概率式17。

P2,T=50=

(17)

经计算得P2,T=50=98.22%，同理，可得边坡未来50年内超越中等损伤的风险概率P3,T=50=68.03%，超越严重损伤的风险概率P4,T=50=29.07%，发生毁坏的风险概率P5,T=50=7.62%。在此基础上，可计算得边坡未来50年内发生各等级震害的风险概率，(表4)。

表4 边坡未来50年内震害风险概率评价结果Table 4 Risk probability assessment results ofthe highway slope in the next 50 years

3 结论

(1)以210国道K359+440边坡为研究对象，采用理论方法开展了边坡震害易损性评价，采用Monte Carlo方法开展了边坡震害风险概率评价。当PGA达到0.7g时，边坡超越严重损伤的概率为53.188%，PGA达到0.8g时，边坡超越严重损伤的概率高达99.086%，未来50年内边坡超越严重损伤的风险概率为29.07%，发生毁坏的风险概率为7.62%。

(2)本文系统地进行了公路边坡震害易损性、地震危险性和风险概率评价，但仍存在以下不足。a:选取边坡顶面横向最大位移dmax作为震害损伤参数，虽具有一定的可行性，但不能全面反应地震对边坡的破坏特点；b:采用Monte Carlo方法进行边坡震害风险概率评价，该方法通过经验公式得到研究场地的PGA分布模型，这种分布模型与研究场地的实际地震危险性存在一定差异。

[1] 甘建军,黄润秋,范崇荣,等.都江堰-汶川公路边坡地震破坏模式研究[J].水文地质工程地质,2011,38(3): 59-65.

GAN Jianjun, HUANG Runqiu, FAN Chongrong, et al. A study of the slope failure along the Dujiangyan to Wenchuan highway after the Wenchuan earthquake[J]. Hydrogeology & Engineering Geology, 2011,38(3): 59-65.

[2] 苏生瑞,李松,程强.汶川地震后公路边坡崩塌灾害发育规律[J].山地学报,2012,30(3):321-327.

SU Shengrui, LI Song, CHENG Qiang. Characteristics of the post-earthquake rock falls of highway slopes in Wenchuan-earthquake stricken areas[J]. Journal of Mountain Science,2012,30(3): 321-327.

[3] LIU Jingwei, WANG Zhenming, XIE Furen, et al. Seismic hazard assessment for greater North China from historical intensity observations [J]. Engineering Geology, 2013(164):117-130

[4] Yiannis T, Nikos L, Prodromos N. Simulating the seismic response of slopes via artificial neural networks [J]. Advances in Engineering Software,2008(40): 640-651.

[5] 徐光兴,姚令侃,李朝红,等.边坡地震动力响应规律及地震动参数影响研究[J].岩土工程学报,2008,30(6):918-923.

XU Guangxing, YAO Lingkan, LI Zhaohong, et al. Dynamic response of slopes under earthquakes and influence of ground motion parameters[J]. Chinese Journal of Geotechnical Engineering,2008, 30(6):918-923.

[6] Yoshihisa Maruyama, Fumio Yamazaki, Kiku Mizuno. Fragility curves for expressway embankments based on damage datasets after recent earthquakes in Japan[J]. Soil Dynamics and Earthquake Engineering, 2010(30):1158-1167.

[7] Luisa Berto, Anna Saetta, Paola Simioni. Structural risk assessment of corroding RC structures under seismic excitation [J]. Construction and Building Materials, 2012(30): 803-813.

[8] 谷音,郑文婷,卓卫东.基于LHS-MC方法的矮塔斜拉桥地震风险概率分析[J].工程力学,2013, 30(8):96-102.

GU Yin, ZHENG Wenting, ZHUO Weidong. Analysis of seismic risk probability assessment of lower-tower cable-stayed bridge based on LHS-MC method [J].Engineering Mechanics, 2013, 30(8):96-102.

[9] 吕大刚,于晓辉.基于地震易损性解析函数的概率地震风险理论研究[J].建筑结构学报,2013,34(10):41-48

LYU Dagang, YU Xiaohui. Theoretical study of probabilistic seismic risk assessment based on analytical functions of seismic fragility [J].Journal of Building Structures,2013,34(10) :41-48

[10] 贾兴利,许金良,武丽娜,等.地震动荷载作用下公路边坡永久位移[J].长安大学学报(自然科学版),2014,34(6):13-18.

JIA Xingli, XU Jinliang, WU Lina, et al. Permanent displacement analysis of road slope under earthquake load[J].Journal of Chang’an University (Natural Science Edition),2014,34(6): 13-18.

[11] 陈鲲,高孟潭.中国大陆地区一般建设工程抗地震倒塌风险研究[J].建筑结构学报,2015, 36(1):23-29.

CHEN Kun, GAO Mengtan. Controlling seismic collapse risk of general construction projects in China mainland [J]. Journal of Building Structure, 2015, 36(1):23-29.

[12] A. Melani, R.K. Khare, R.P. Dhakal. Seismic risk assessment of low rise RC frame structure [J]. Structures, 2016(5):13-22.

[13] 沈怀至,金峰,张楚汉.基于性能的重力坝-地基系统地震易损性分析[J].工程力学,2008,25(12):86-91.

SHEN Huaizhi, JIN Feng, ZHANG Chuhan. Performance based seismic fragility analysis of concrete gravity foundation system [J]. Engineering Mechanics, 2008, 25(12):86-91.

[14] Karthik R, Jamie P, Reginald D. Temporal evolution of seismic fragility curves for concrete box-girder bridges in California Engineering [J].Structures, 2015(97): 29-46.

[15] 生命线工程地震破坏等级划分(GB/T 24336—2009)[S].北京:人民交通出版社,2009.

Seismic damage hierarchies of lifeline engineering (GB/T 24336—2009) [S].Beijing: People’s Transportation Press, 2009.

[16] 宗亮,王元清,杨赛霓,等.基于HAZUS平台的中国公路桥梁震害评估模型研究[J].土木工程学报,2014,47(s1):263-268.

ZONG Liang, WANG Yuanqing, YANG Saini, et al. Research on highway bridges seismic damage assessment system for China based on HAZUS [J].China Civil Engineering Journal, 2014, 47(s1): 263-268.

[17] 汪旭,康飞,李俊杰.土石坝地震永久变形参数反演方法研究[J].岩土力学,2014,35(1):279-286.

WANG Xu，KANG Fei，LI Junjie. Back analysis of earthquake-induced permanent deformation parameters of earth-rock dams [J].Rock and Soil Mechanics, 2014, 35(1): 279-286.

[18] 孙发权.公路填方路基结构的振动台模拟试验研究[J].重庆:重庆交通大学,2010.

SUN Faquan. The vibration of highway subgrade filled physical simulation tests [D]. Chongqing: Chongqing Jiao Tong University, 2010.

[19] TANG Chuan, ZHU Jing, LIANG Jingtao. Emergency assessment of seismic landslide susceptibility: a case study of the 2008 Wenchuan earthquake affected area [J]. Earthquake Engineering & Engineering Vibration, 2009 (8): 207-217.

[20] Wu D, Tesfamariam S, Stiemer S F, et al. Seismic fragility assessment of RC frame structure designed according to modern Chinese code for seismic design of buildings [J]. Earthquake Engineering & Engineering Vibration, 2012(11): 331-342.

[21] WANG Qiang, WU Ziyan, LIU Shukui. Seismic fragility analysis of highway bridges considering multi-dimensional performance limit state [J]. Earthquake Engineering and Engineering Vibration, 2012(11):185-193.

RiskprobabilityassessmentofhighwayslopeseismicdisasterbasedonIDA-MCmethod

YU Wei1,2,SHE Xuesen1,2

(1.HighwaySchool,Chang′anUniversity,Xi′an,Shaanxi710064,China; 2.KeyLaboratoryforSpecialAreaHighwayEngineeringofMinistryofEducation,Chang′anUniversity,Xi′an,Shaanxi710064,China)

A risk probability assessment method of highway slope seismic disaster was proposed, which can enhance highway slope seismic capacity. K359+440 slope of G210 was selected as the research object, Incremental Dynamic Analysis(IDA) was used to carry out the highway slope seismic fragility assessment, the fragility curve was obtained, as well as the damage probabilities under certain Peak Ground Accelerations(PGAs). The risk probabilities of all seismic damage levels of the highway slope in the next 50 years were calculated using Monte Carlo(MC) method based on study of the distribution characteristics of ground motion. The results show that when PGA is 0.7 g, the probability exceeding severe damage is 53.188%, when PGA is 0.8 g, the probability is 99.086%; In the next 50 years, the risk probability exceeding severe damage is 29.07%, the risk probability of destruction is 7.62%.

highway slope; seismic disaster; Incremental Dynamic Analysis(IDA); fragility; Monte Carlo(MC) method; risk probability assessment

U416.02

A

1003-8035(2017)03-0024-07

10.16031/j.cnki.issn.1003-8035.2017.03.04

2016-10-08;

2017-02-17

西部交通建设科技项目(2009353361420)

于 伟(1980-)，男，山东潍坊人，博士研究生，主要从事岩土工程方面的研究。E-mail：chdyuwei1@163.com