膨胀土分类的改进TOPSIS法及应用
赵国彦,李 鑫,梁伟章
(中南大学资源与安全工程学院,湖南 长沙 410083)
膨胀土分类的改进TOPSIS法及应用
赵国彦,李 鑫,梁伟章
(中南大学资源与安全工程学院,湖南 长沙 410083)
针对传统TOPSIS法的不足,提出一种膨胀土分类的改进TOPSIS法。选取能充分反映膨胀土胀缩特性的液限、塑性指数、小于2 μm胶粒含量与自由膨胀率为指标进行分析。综合考虑样本数据的波动信息与独立信息,采用独立信息数据波动(DIDF)赋权法确定权重。然后将灰色关联分析(GRA)与TOPSIS法融合,结合指标权重计算指标分类标准与待分类样本的贴近度。通过比较样本与各类别贴近度的大小确定所属类别,同时还可对同一类别膨胀土胀缩性进行排序,为工程建设提供更详细的参考依据。最后,选取2个工程实例共32个膨胀土样本对所建立模型进行验证。结果表明,该方法分类结果与实际较吻合,准确率平均达90.63%,能满足工程需要。
膨胀土;逼近理想解排序法;灰色关联分析;独立信息数据波动赋权法;分类
0 引言
膨胀土是我国分布广泛的一种富含强亲水性矿物的高塑性黏土[1-2]。由于它具有长期、反复随湿度变化的胀缩特性,常给工程建设带来巨大挑战与危害,素有“工程癌症”之称[3]。对膨胀土分类目的是将胀缩性相同的膨胀土分为同一类型,为工程建设提供指导[4]。若对膨胀土类别进行了漏判或误判,将给工程建设埋下隐患,甚至造成重大灾害事故[1-4]。
国内外关于膨胀土分类已有诸多研究,主要分为单因素分类法与多因素分类法。单因素分类法简单、易于工程应用,如风干含水量分类法[5]、塑性图分类法[6]等。由于影响膨胀土胀缩性的因素较多,且指标取值往往存在随机性与模糊性,故单因素分类法具有一定片面性。多因素分类法综合考虑了多个指标,应用模糊数学[7]、多元回归分析[8]、距离判别分析[9]、Fisher判别分析[10]、物元可拓模型[11]、云模型[12]等进行分析,被证明是一种有效的膨胀土分类手段。以上方法取得了一定效果,但由于膨胀土本身的复杂性与相关理论的局限性,目前仍未有一种方法适用于所有的工程环境。
TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)法是一种有效的多目标决策分析法[13-15]。通过比较决策对象与最优、最劣解的接近程度进行排序,具有较好的客观性,已广泛应用于岩爆预测[13]、水质评价[14]、风险控制[15]等领域。为此,笔者借鉴TOPSIS法的思想,并针对其不足,提出一种膨胀土分类的改进TOPSIS模型。通过采用独立信息数据波动(DIDF)赋权法确定指标权重,应用灰色关联分析(GRA)对TOPSIS法进行改进,然后采用Euclidean距离计算决策方案与理想方案的贴近度,最后引用相关文献实例验证该方法的可行性,为膨胀土分类提供一个新思路。
1 TOPSIS法及其改进
1.1传统的TOPSIS法
TOPSIS法是由C.L.Hwang和K.Yoon于1981年首次提出。其基本原理是:依据决策方案各指标属性,分别选择一组最优与最劣指标值为正、负理想方案,通过比较各方案与正、负理想方案的距离确定最优方案[16]。传统的TOPSIS法在多目标决策领域取得了较好效果,但也存在一些问题,主要如下:
(1) 由于样本资料有限,且存在人为因素影响,许多指标数据波动较大,无典型分布规律。若直接采用样本数据进行分析,难以保证结果的准确性;
(2) 对各指标权重的确定需充分考虑指标数据自身提供的信息,应同时分析同一指标数据间及不同指标数据间的客观差异性。
1.2改进的TOPSIS法
针对上述问题,笔者对传统的TOPSIS法进行改进,提出一种改进的TOPSIS分类法。
该方法针对问题(1),引入灰色关联分析(GRA)思想。灰色关联分析是一种通过比较各样本数据间变化态势来判断各指标间关联程度的多因素统计分析法,对数据要求较低且计算量小,无需数据具有典型分布规律,其核心是计算关联度[17]。将GRA与TOPSIS法相结合,既保留 TOPSIS 法客观性好的优点,又充分利用GRA在贫信息下易于挖掘数据规律的优势。
该方法针对问题(2),引入独立信息数据波动(DIDF)赋权法确定权重。样本指标数据自身可提供2种信息:①数据波动信息,指同一指标在均值附近的波动程度。一般用离差系数表示,即标准差与平均值之比。离差系数越大,表示数据波动越大,提供信息越多。反之,提供信息越少;②独立信息,指各指标间的相关程度。指标之间往往存在一定相关性,在决策过程中会带来重复计算而降低精度。若某指标与其他指标间拟合优度为R2,则该指标提供的独立信息程度为1-R2。若R2为0,则该指标可提供完全信息。若R2为1,则该指标不能提供任何信息,可将其取消[18]。
改进的TOPSIS法计算步骤如下:
(1) 建立标准化决策矩阵
选取指标分类区间下限值与样本指标值构成决策矩阵Amn=(aij)mn。
(1)
式中:k——类别总数,矩阵中前k行为各分类区间下限值,其它为各样本指标实测值,共(n-k)个样本。
对矩阵A进行无量纲处理,得到标准化决策矩阵Bmn=(bij)mn。
对于越大越优型指标
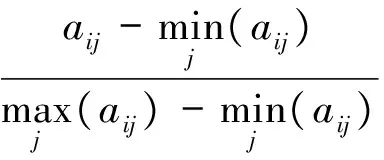
(2)
对于越小越优型指标
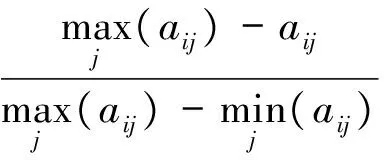
(3)
(2) DIDF赋权法确定指标权重
结合数据波动信息与独立信息确定指标权重,具体步骤如下:
①计算各指标离差系数Vj

(4)
式中:δj——标准差;


(5)
③计算各指标纯信息量Ij
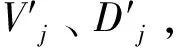
(6)
(7)
(8)
④计算各指标权重

(9)
(3) 构建加权标准化决策矩阵
将标准化矩阵B与权重Wj相乘,得到加权标准化决策矩阵Cmn=(cij)mn。
cij=bij×Wj
(10)
(4) 确定加权标准化决策矩阵正理想解
对于越大越优型指标
(11)
对于越小越优型指标
(12)
(5) 计算决策对象与正理想解的灰色关联系数Rmn=(rij)mn
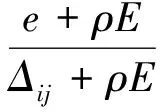
(13)

(6) 确定灰色关联系数矩阵正、负理想解
(14)
(7) 计算决策对象与正、负理想解的Euclidean距离
(15)
(8) 计算决策对象与正理想解贴近度
(16)
(9) 计算趋近度以确定各样本隶属类别
通过比较样本与各等级贴近度大小确定样本所属级别。若样本贴近度值小于1级或大于k级,则样本所属等级为1级或k级;若样本贴近度值位于两相邻等级之间,则通过计算样本贴近度与两相邻等级的趋近度α来确定等级归属。
(17)


若α>1,样本类别为第t级;
若α<1,样本类别为第t+1级;
若α=1,设越大越优型指标权重和为S1,越小越优型指标权重和为S2,当S1>S2,样本类别为第t+1级;当S1 影响膨胀土胀缩性指标多达十几个,主要有直接指标法与间接指标法[4]。直接指标法直观,但测试手段复杂,要求测试人员具有较高专业技能,如选用膨胀量、收缩量、矿物含量等指标;间接指标法不够直观,但测试方法简单,具有一定合理性,如选用液限、塑限、自由膨胀率等指标。工程中常选用间接指标法进行分类。 对国内外膨胀土分类采用的指标进行统计分析[1-12],结果表明:液限、塑性指数、粒度组成与自由膨胀率4个指标被选用频率最高。液限表示土体呈可塑状态的上限含水率,塑性指数表示土体呈塑性状态的含水量范围,两者均与土的粒径组成、黏性矿物含量、比表面积等关系密切[7];粒度组成是反映膨胀土物质组成特性的基本指标,土中小于2 μm胶粒含量越高,表明蒙脱石成分越多,亲水性越强,膨胀性越大[4];自由膨胀率直接反映土的胀缩特性,黏性矿物含量越高,亲水性越强,自由膨胀率越大[10]。 因此,文中选用液限X1、塑性指数X2、小于2 μm胶粒含量X3与自由膨胀率X4作为分析指标。参考《膨胀土地区建筑技术规范(GBJ112-87)》[19]、《公路路基设计规范(JTG D30-2004)》[20]以及相关文献[4-7],将膨胀土分为强膨胀土(I)、中等膨胀土(II)、弱膨胀土(III)与非膨胀土(IV)四个类别,各指标分类标准见表1。 为验证所建立的改进TOPSIS膨胀土分类方法的有效性,文中以2个膨胀土工程实例进行分析。 选取文献[7]中当-宜高速公路与文献[10]中合-六-叶高速公路共32个膨胀土样本进行分析,样本实测值见表2。依据表1各指标分类区间下限值及表2样本实测值建立决策矩阵A。 表1 胀缩土分类标准Table 1 Classification standard of expansive soil 表2 膨胀土样本与分类结果Table 2 Samples of expansive soils and classification results 由式(2)~(3)对矩阵A进行无量纲处理,得到标准化决策矩阵B。 由式(4)~(9)计算指标权重,结果见表3。由于液限是指土体由流动状态变为可塑状态的界限含水量,与土的粒径组成、黏性矿物含量、比表面积等关系较密,因而与其他指标相关性较高。文中计算的相关性达0.958,可能取用了与其他指标包含的重复信息,且该指标提供的独立信息程度较低,故权重较小;而自由膨胀率是反映土胀缩特性的直接指标,与其他指标的相关性较低,且提供的独立信息程度较高,因而权重较大。 表3 权重计算结果Table 3 Calculation results of weights 由式(10)构建加权标准化决策矩阵C。 由式(11)~(13)计算决策对象与正理想解的灰色关联系数R。 由式(14)得灰色关联系数矩阵正、负理想解。 r+=[1.0000,1.0000,1.0000,1.0000] r-=[0.3333,0.3333,0.3333,0.3333] 由表2可知,文中方法分类与引用文献中分类结果基本一致,文献[7]中当-宜高速公路实例只有样本3、9分类结果不同,准确率为86.67%;文献[10]中合-六-叶高速公路实例只有样本28分类结果不同,准确率为94.12%;两个工程实例平均分类准确率达90.63%。同时,文中对评判有误的样本3、9、28应用模糊综合评判法[7]进行判别,得到判别向量分别为:G3=(0, 0.545 2, 0.275 6, 0.179 2)、G9=(0, 0, 0, 1)、G28=(0.574 1, 0.235 9, 0.190 0, 0),根据最大隶属度原则,样本3、25、28所属类别应分别为中等膨胀土、非膨胀土、强膨胀土,与文中方法判别结果一致。同时,文中还与传统TOPSIS法进行了对比分析,计算结果见表2。当-宜高速公路分类准确率为73.33%,合-六-叶高速公路分类准确率为64.71%,两个工程实例平均分类准确率为69.02%。由于计算过程中未考虑各指标权重的差异性,指标权重取值均为0.25,且未采用灰色关联法对原数据进行进一步关联处理,故计算结果存在较大偏差。因此,文中建立的膨胀土分类模型误差在可接受的范围内,能满足工程要求,可作为一种有效的膨胀土分类方法。 同时,该方法还可对同一类别的膨胀土胀缩性进行排序,为工程建设提供更详细的指导。以非膨胀土为例,样本9、16、17、18分类结果均为非膨胀土类型,但与正理想解的贴近度并不一致,各样本膨胀性大小也不相同。可根据贴近度大小对其进行排序,膨胀性由大到小排序结果为:样本17>18>9>16。其中,样本17与正理想解的贴近度为0.217 7,接近弱膨胀土类型的下限值0.237 6,在工程中易转化为弱膨胀土,因此需更加重视。其它类型膨胀土可采用类似方法进行排序,对具有较强膨胀性趋势的膨胀土需加强管理,并采取有效处理措施。 针对传统TOPSIS法存在的不足,提出一种改进的TOPSIS分类方法,并将其应用于膨胀土分类中,提高了判别精度,得出如下结论: (1) 运用TOPSIS法计算膨胀土样本、各分类区间下限值与正理想解的贴近度,不仅可对膨胀土胀缩性进行分类,还可根据贴近度的大小对同一类别膨胀土进行排序,为工程建设提供更详细的参考依据; (2) 将GRA与 TOPSIS 法相结合,保留了两者的优点,克服了在样本资料有限的情况下,指标数据波动较大且无典型分布规律的缺陷; (3) 采用DIDF赋权法确定指标权重,综合考虑了样本数据的波动信息与独立信息,是一种有效的客观赋权法; (4) 结合2个膨胀土工程实例,对所建立的改进TOPSIS膨胀土分类法进行验证,分类结果与文献结果具有较高的一致性,平均准确率达90.63%,可满足工程需要。 [1] SHI B, JIANG H, LIU Z, et al. Engineering geological characteristics of expansive soils in China[J]. Engineering Geology, 2002, 67(1-2): 63-71. [2] 张连杰, 武雄, 谢永, 等. 含水量及上覆压力对重塑膨胀土抗剪强度的影响分析[J]. 中国地质灾害与防治学报, 2015,26(4): 138-143. ZHANG Lianjie,WU Xiong,XIE Yong, et al. Influence of water content and overlying pressure on shear strength of remolded expansive soil[J]. The Chinese Journal of Geological Hazard and Control, 2015,26(4): 138-143. [3] WANG M, LI J, GE S, et al. Moisture migration tests on unsaturated expansive clays in Hefei, China[J]. Applied Clay Science, 2013, 79: 30-35. [4] 陈善雄, 余颂, 孔令伟, 等. 膨胀土判别与分类方法探讨[J]. 岩土力学, 2005, 26(12): 1895-1900. CHEN Shanxiong, YU Song, KONG Lingwei, et al. Study on approach to identification and classification of expansive soils[J]. Rock and Soil Mechanics, 2005, 26(12): 1895-1900. [5] 谭罗荣, 张梅英,邵梧敏,等. 风干含水量W65用作膨胀土判别分类指标的可行性研究[J]. 工程地质学报, 1994, 2(1): 15-26. TAN Luorong, ZHANG Meiying, SHAO Wumin, et al. The practicability research on use of air dry moisture contentW65as identification index of the swelling soil[J]. Journal of Engineering Geology, 1994, 2(1): 15-26. [6] 马桂芝. 应用塑性图对陕西特殊土的判别[J]. 西安地质学院学报, 1995, 17(2): 87-89. MA Guizhi. The application of plasticity chart to shanxi special soils distribution[J]. Journal of Xi’an College of Geology, 1995, 17(2): 87-89. [7] 郭昱葵, 熊友山, 姚海林, 等. 模糊数学在当宜高速公路膨胀土判别和分类中的应用[J]. 岩土力学, 1999, 20(3): 61-65. GUO Yukui, XIONG Youshan, YAO Hailin, et al. Application of fuzzy mathematics in classification of expansive soils for expressway from Dangyang to Yichang[J]. Rock and Soil Mechanics, 1999, 20(3): 61-65. [8] YILMAZ I. Indirect estimation of the swelling percent and a new classification of soils depending on liquid limit and cation exchange capacity[J]. Engineering Geology, 2006, 85(3-4): 295-301. [9] 宫凤强, 李夕兵. 膨胀土胀缩等级分类中的距离判别分析法[J]. 岩土工程学报, 2007, 29(3): 463-466. GONG Fengqiang, LI Xibing. Distance discriminant analysis to the classification of the grade of shrink and expansion for the expansive soils[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 463-466. [10] 余颂, 陈善雄, 余飞, 等. 膨胀土判别与分类的Fisher判别分析方法[J]. 岩土力学, 2007, 28(3): 499-504. YU Song, CHEN Shanxiong, YU Fei, et al. Fisher’s discriminant analysis method for identification and classification of expansive soil[J]. Rock and Soil Mechanics, 2007, 28(3): 499-504. [11] 李颢, 张风安. 物元可拓模型对内蒙古地区膨胀土判别的应用[J]. 中国地质灾害与防治学报, 2010, 21(1): 114-116. LI Hao,ZHANG Fengan. Application of matter-element extension model in grading expansive soils in Inner Mongolia Areas[J]. The Chinese Journal of Geological Hazard and Control, 2010, 21(1): 114-116. [12] 汪明武, 李健, 徐鹏, 等. 膨胀土与石灰改良膨胀土胀缩性的云模型评价[J]. 东南大学学报(自然科学版), 2014(2): 396-400. WANG Mingwu, LI Jian, XU Peng, et al. Cloud model for shrinkage-swelling property classification of untreated and lime-treated expansive clays[J]. Journal of Southeast University(Natural Science Edition) , 2014(2): 396-400. [13] 周科平, 雷涛, 胡建华. 深部金属矿山RS-TOPSIS岩爆预测模型及其应用[J]. 岩石力学与工程学报, 2013(S2): 3705-3711. ZHOU Keping, LEI Tao, HU Jianhua. Rs-topsis model of rockburst prediction in deep metal mines and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2013(S2): 3705-3711. [14] BHUPINDER S, SUDHIR D, SANDEEP J, et al. Use of fuzzy synthetic evaluation for assessment of groundwater quality for drinking usage:a case study of southern Haryana, India[J]. Environmental Geology, 2008, 54(2): 249-255. [15] 张志峰, 白焱. 基于综合赋权C-TOPSIS法的航天器研制风险控制[J]. 东北大学学报(自然科学版), 2015, 36(5): 626-630. ZHANG Zhifeng, BAI Yan. Risk control of the spacecraft development based on comprehensive weight C-TOPSIS[J]. Journal of Northeastern University(Natural Science), 2015, 36(5): 626-630. [16] 徐玖平, 吴巍. 多属性决策的理论与方法[M]. 北京: 清华大学出版社, 2006. XU Jiuping, WU Wei. Multiple attribute decision making theory and methods[M]. Beijing: Tsinghua University Press, 2006. [17] 刘思峰, 郭天榜, 党耀国, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 1999. LIU Sifeng, GUO Tianbang, DANG Yaoguo, et al. Frey system theory and its applications[M]. Beijing: Science Press, 1999. [18] 俞立平, 潘云涛, 武夷山. 一种新的客观赋权科技评价方法——独立信息数据波动赋权法DIDF[J]. 软科学, 2010, 24(11): 32-37. YU Liping, PAN Yuntao, WU Yishan. A new objective weighting method of sci-tech evaluation —— independent information data fluctuation weighting method DIDF[J]. Soft Science, 2010, 24(11): 32-37. [19] GBJ112-87, 膨胀土地区建筑技术规范[S]. GBJ112-87, Architectural technical code of expansive soil area[S]. [20] JTGD30-2004, 公路路基设计规范[S]. JTGD30-2004, Specification for design of highway subgrades[S]. ImprovedTOPSISmethodfortheclassificationofexpansivesoilsanditsapplication ZHAO Guoyan,LI Xin,LIANG Weizhang (SchoolofResourcesandSafetyEngineering,CentralSouthUniversity,Changsha,Hunan410083,China) Aiming at the issues of traditional TOPSIS method, an improved TOPSIS method for the classification of expansive soils was proposed. Four classification indexes which can reflect the swell-shrink characteristics of expansive soils including liquid limit, plasticity index, clay particles, free swell ratio were chosen. Both wave information and independent information of samples data were considered comprehensively, and a new independent information data fluctuation weighting method was used to calculate the weights. Then, the grey relational analysis and TOPSIS method were integrated, and the closeness degrees of the classification standards of indexes and samples were calculated by combining with the weight values. The classification of expansive soils was specified by comparing the magnitude of closeness degrees. This method can also arrange the order of swell-shrink characteristics in the same category, which can provide more detailed reference for engineering construction. Finally, the classification method of expansive soils was validated with 32 testing examples from 2 engineering projects. The results show that the classification results satisfyingly agree with the measured data at the average accuracy of 90.63%, which can satisfy the engineering demand. expansive soil; technique for order preference by similarity to an ideal solution; grey relational analysis; independent information data fluctuation weighting method; classification TU443 A 1003-8035(2017)03-0130-07 10.16031/j.cnki.issn.1003-8035.2017.03.20 2016-12-02; 2017-01-20 国家自然科学基金面上项目(51374244);国家重点基础研究发展计划(973)项目(2010CB732004) 赵国彦(1963-),男,博士,教授,主要从事矿山安全与岩石力学等领域研究。E-mail: gy.zhao@263.net2 分类指标的选取
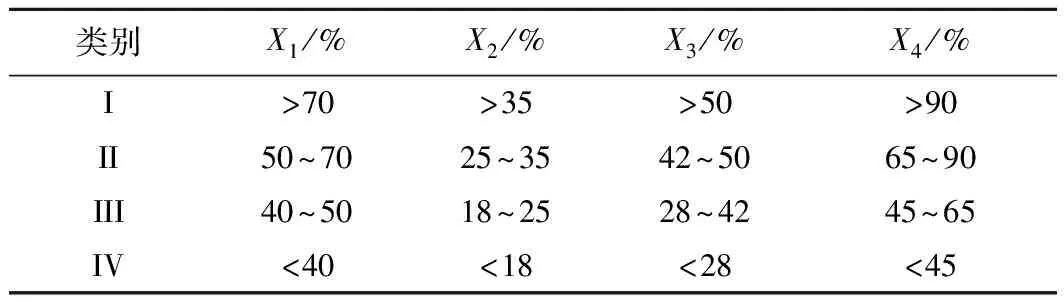
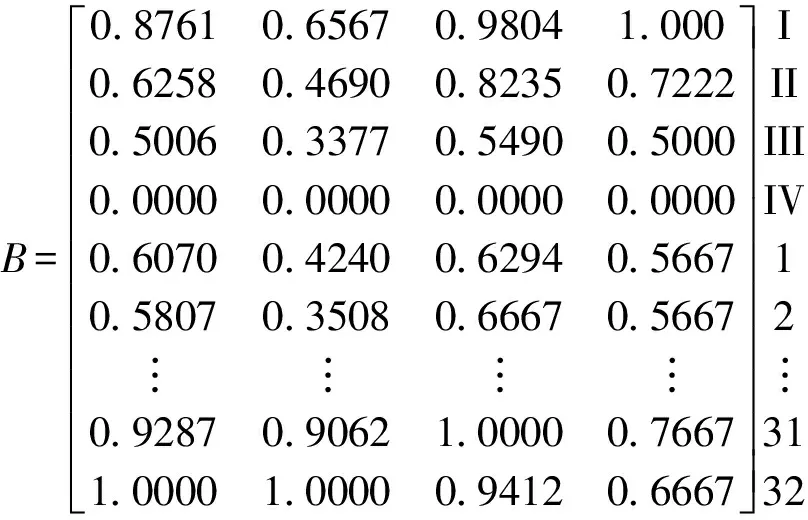
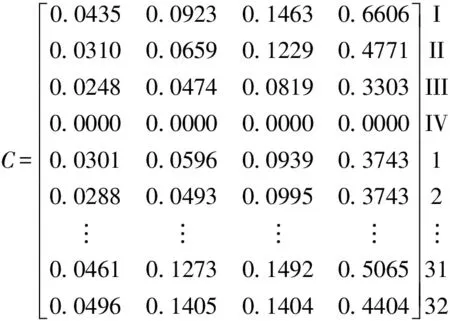
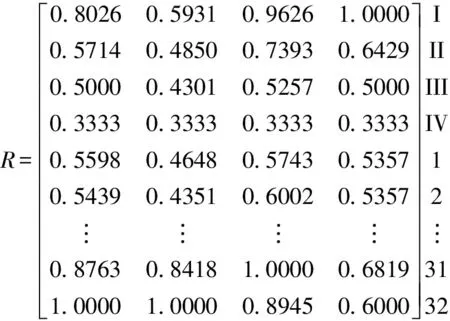
3 工程应用




4 结论

