竖井钢罐道受力体系影响因素分析
王建中,郭相参,姚 心
(中国恩菲工程技术有限公司,北京100038)
综合技术
竖井钢罐道受力体系影响因素分析
王建中,郭相参,姚 心
(中国恩菲工程技术有限公司,北京100038)
竖井钢罐道水平荷载受多种因素的影响,设计中一般采用简化的经验公式进行计算,但随着高速、深竖井的应用,经验公式已无法满足设计要求。基于此,分析了影响钢罐道水平力的各种因素,并利用仿真软件FLUENT对空气动力的影响进行了重点分析,通过分析总结出水平荷载的通用函数,为相关从业者提供借鉴。
水平荷载; 影响因素; 仿真软件; 通用函数
1 前言
随着井筒深度的不断增加,以及提升终端荷载和提升速度的大幅提高,现行用于确定钢罐道水平荷载计算的经验公式已难以满足提升竖井井筒装备的设计计算要求。基于竖井提升容器采用钢罐道时以水平力为主进行井筒装备的设计,本文对钢罐道所受水平力及其影响因素进行分析和研究,给出了水平力的函数表达式。
2 水平荷载设计现状
提升容器在竖井中运行时与钢罐道发生不间断的碰撞,该作用力即为钢罐道水平荷载。设计中常将该空间受力体系简化为平面受力体系,见图1。

图1 钢罐道受力图
多年来,钢罐道的设计荷载一般按照原联邦德国在《竖井与斜井装备的技术规程》(1977年)中提出的水平力经验公式确定。该公式源于20世纪30年代初别尔教授对30多个井筒的调查,是基于当时的井筒装备技术条件和罐道梁层间距(3m)得出的经验公式:
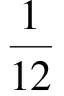
(1)
Fz=0.8Fh
(2)
Fv=0.25Fh
(3)
式中:G——最大终端提升荷载,kN;
γo——结构重要性系数,取γo=1.1;
γQ——活荷载分项系数,取γQ=1.4;
Fh——正面水平力,kN;
Fz——侧面水平力,kN;
Fv—垂直力,kN。
我国从1977年至1986年对11个竖井井筒装备进行了水平力测试,文献[2]给出了水平力测试结果的汇总表,见表1。

表1 钢罐道正面水平力测试结果汇总表
罐道及罐道梁上所受的设计荷载按下列公式计算:
Fh=γoγQFhk
(4)
Fz、Fv计算同上述(2)、(3)式。
式中:Fhk——水平力,按表1选取,kN;
其它符号同前。
工程设计中,对于小型矿山,最大终端提升荷载较小时,采用公式(1)~(3)计算水平力;对于大、中型矿山,最大终端提升荷载小于30t,提升速度小于14m/s时,采用公式(4)、(2)、(3)计算水平力。
3 水平力影响因素分析
如果钢罐道是一个绝对垂直、光滑的平行轨道,且在上面运行的设备没有偏心和摆动,则罐道的水平力很小,但实际情况并非如此。考虑到钢罐道水平力主要受侧向和正向两个方向的作用且两者关系一定,本文仅对钢罐道正面水平力(Fh)进行研究,综合国内外研究成果,该力主要受井筒装备安装和提升设备的缺陷、设备终端荷载、设备提升速度等因素的影响。
3.1 井筒装备安装和提升设备的缺陷δ
井筒装备安装精度和提升设备的制造缺陷是产生水平力的主要原因。罐道接头处的突起或凹陷、滚轮罐耳缺陷、提升容器不平衡、提升容器与罐道的不合理配合以及提升设备结构的不合理均会引起提升设备的摆动。设备的摆动均会引起罐道梁水平力的增加。其本质是设备在运行过程中因外部干扰而导致重心与形心不能完全重合或出现较大偏差而导致设备产生偏心。设备偏心越严重,设备与罐道之间的碰撞越明显,水平力越大。
随着设备加工技术的不断提高,因设备本身产生的偏心问题可以得到有效控制,但井筒装备的安装因受人为因素的影响,很难完全消除。多个国家对井筒水平力进行过现场实测,中国矿业大学在1991年对大屯副井水平荷载现场实测见图2,南非金山大学教授G.J.Krige于1986年对南非的两条主井水平荷载现场实测见图3。
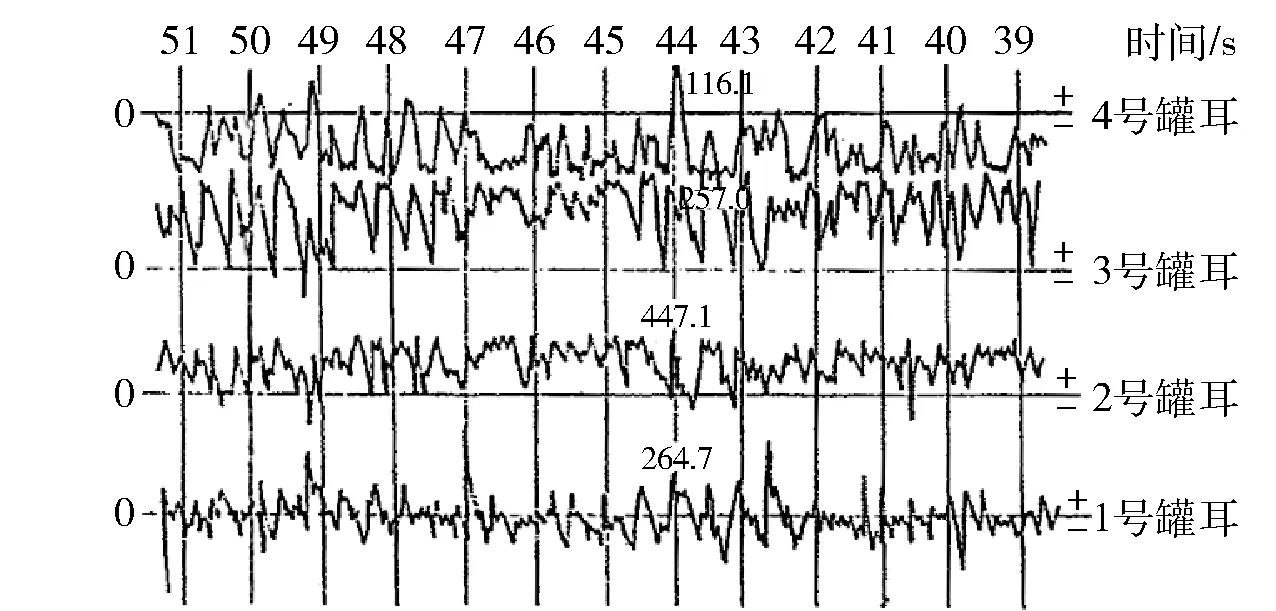
图2 大屯副井水平荷载实测波形图
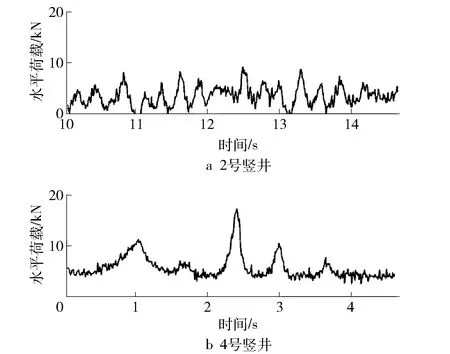
图3 滚轮荷载实测波形图
由图2和图3可知,水平力具有随机性和不确定性的特点,但均在一定的范围内波动,这主要是因为井筒安装须按照相应的安装规范进行,因此,水平力也具有一定的规律性,这为水平力的计算提供了依据。
3.2 设备终端荷载Q
西德在1957年《采矿工程》中提出罐道梁水平力与终端荷载有关。国内在此研究基础上并结合本国情况,总结出了与提升速度和终端荷载有关的水平力经验公式(见公式(4)、(2)、(3))。国内外的研究和现场实测均表明终端荷载是影响水平力的主要因素,且随着终端荷载的增加而增加。
3.3 设备提升速度v
中国矿业大学在20世纪90年代对大屯副井的实测表明,在相同终端荷载情况下(Q=16.1t),v=8.4m/s时,水平力为10.9kN;v=3.1m/s时,水平力为5kN。水平力受提升速度影响较大,且随着提升速度的增加而增加。
前苏联对井筒装备的动态分析表明,水平力与提升速度的平方成正比;国内中国矿业大学现场实测资料表明水平力与提升速度的一次方成正比;图4为南非金山大学教授G.J.Krige于1986年对南非5条竖井的实测和预测结果对比图,从图中可知,除竖井4中水平力与提升速度呈指数关系外,其余竖井中水平力与提升速度基本呈线性关系。
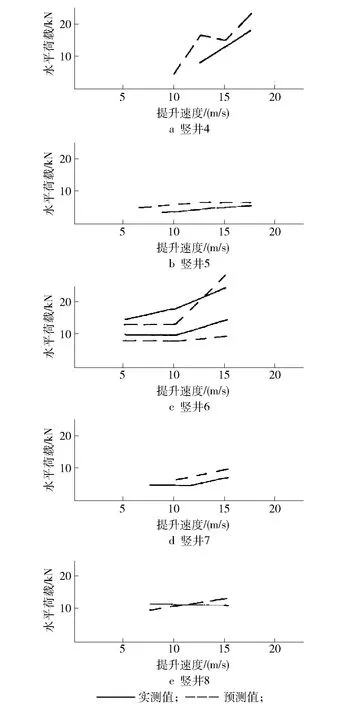
图4 速度与水平力关系图
3.4 罐道梁层间距L
层间距L对井筒装备的承载力有影响,层间距越大,跨度越大,承载能力越小。国内外研究表明,增大层间距对减小水平力有一定的作用,这是因为L增大时井筒装备的整体刚度C减小,刚度的减小能够吸收容器的部分冲击力,与水平荷载呈非线性关系,图5为南非金山大学教授G.J.Krige于1986年对南非主井现场实测结果。
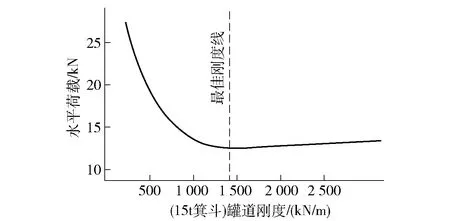
图5 罐道刚度与水平力关系图
3.5 井筒装备整体刚度C
井筒装备的整体刚度是一个综合指标,它反映的是单位变形条件下在变形方向所施加力的大小。刚度与井筒装备布置型式、材料性质、几何形状、边界支持情况以及外力作用形式有关。国内外研究中对刚度的处理不尽相同,中国矿业大学研究认为井筒内不同区段由于装配不同,刚度是一个不确定量,同时考虑到罐道梁层间距对刚度的影响很大,在研究中利用层间距反应井筒装备的结构性能包括刚度;南非、波兰、澳洲几家研究机构在水平力计算中单独考虑了刚度的影响,但表现形式多样,并不局限于装备的整体刚度。水平荷载分析时,尤其是在物理模拟时,为减小各种因素对计算结果的影响,可以不考虑该因素的影响。
3.6滚轮罐耳预压力Fj
该力通过滚轮罐耳预先施加在罐道上,该力不大,为定值,对水平力有一定的影响,但影响有限,可以作为水平力的额外受力进行考虑或者作为综合系数统一考虑。
3.7提升钢丝绳开捻力矩的作用Fn
普通钢丝绳一般由数根(通常是6根)钢绳捻制而成,顺捻钢丝绳承重后会产生一定的扭力,即为钢丝绳开捻力矩。该力在提升容器上产生一个平面力偶导致提升容器横向摆动,与罐道间发生不断的作用,这是一个反复作用的过程,但多绳提升钢丝绳一般通过布置方式减小开捻力矩的影响,根数一般为偶数,且一半采用左捻,另一半采用右捻,并相互交错并列,钢丝绳的开捻力矩基本可互相抵消,因此在水平力分析时暂不考虑该力的作用。
3.8科里奥利(Coriolis)力Fg
科里奥利(Coriolis)力,简称科氏力,是旋转体系中进行直线运动的质点由于惯性作用产生的力。将地球作为研究对象,设备沿罐道上下运动可简化为直线运动,地球的自转便产生了科氏力,此力作用在容器质心,大小和方向由下式确定:
(5)
(6)
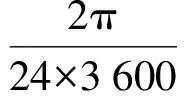
(7)
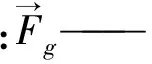
m——容器加载荷总质量,kg;


α——容器运行速度矢量正向与地球转动角速度矢量正向的夹角。
由公式(5)~(7)可知,科氏力Fg主要受Q(Q=m·g)和v的影响,且与Q和v呈线性关系。
由可控源地震学数据分析得出的模型可用地下弹性/非弹性性质(特别是P波速度VP、S波速度VS和密度ρ)表示。将弹性地球模型分解为背景变量(即长波长)和短波长波动(通常被称作反射率,速度和密度的乘积,称为地震波阻抗),可得出可控源地震学的两个主要分支。第一个是广角反射/折射(WARR)法(有时也被称为深地震探测方法),可以提供有关全球构造的信息(该方法的近期历史回顾见Prodehl and Mooney,2012)。第二个是地震勘探的典型手段——所谓的近垂直入射反射法(NVI),它能提供高分辨率的地球反射系数图像。
以位于北纬41°的某高速、深竖井为例计算科氏力。该竖井深1 445m,井筒内配30m3双箕斗,箕斗有效载荷56t,箕斗自重约60t,最大提升速度18.025m/s,则:
m=(60+56)×103=1.16×105kg
Fg=2mωrvsinα
=2×1.6×105×2.314×10-5π×18×sin41°
=199 N
容器上行时,方向由西向东;容器下行时,方向由东向西。该力远远小于钢罐道水平力,公式计算时可忽略不计,设计时稍加考虑即可。
3.9空气动力Fa
提升设备在井筒中运行时,由于气流对井壁和提升设备的摩擦作用,致使井筒内产生较大的活塞风流和瞬态变化的井筒压力,引发相应的空气动力学效应,从而引起流场对提升设备产生压力差。由于提升设备周围的压力并不一致,因此在设备周围产生了压力差,在该压力差的作用下,提升设备会向压强较弱侧摆动并与罐道梁发生碰撞从而产生水平力。随着提升深度的增加,设备运行速度也在增加,空气动力对设备的影响更为明显。
综上所述,钢罐道正面水平力(Fh)主要受井筒装备安装和提升设备的缺陷(δ)、设备终端荷载(Q)、设备提升速度(v)、罐道梁层间距(L)、井筒装备的整体刚度(C)、滚轮罐耳预压力(Fj)的影响,提升钢丝绳开捻力矩的作用(Fn)和科里奥利(Coriolis)力(Fg)的影响可以忽略不计;但对于空气动力(Fa)却无法通过简单的分析和计算判断其对水平力的影响,通常需要通过模拟来确定。
4 基于FLUENT的空气动力模拟
为了更好地分析空气动力对水平力的影响,利用仿真软件FLUENT模拟了双箕斗在井筒中的运行情况。模拟中假定箕斗的规格一致,变化的仅是井筒直径和提升速度。
FLUENT是目前国际上比较流行的商用CFD(Computational Fluid Dynamics)软件包,在航空航天、汽车设计、石油天然气和涡轮机设计等方面都有着广泛的应用。FLUENT可用来模拟从不可压缩到高度可压缩范围内的复杂流动,凡是和流体、热传递和化学反应等有关的工业均可使用,它具有丰富的物理模型、先进的数值方法和强大的前后处理功能,由于采用了多种求解方法和多重网格加速收敛技术,因而能达到最佳的收敛速度和求解精度。
4.1 计算模型简化
通过上述分析可知,水平力的主要影响因素为:安装和设备缺陷δ、提升终端荷载Q、提升速度v、罐道梁层间距L、装备整体刚度C和空气动力Fa。
提升终端荷载Q的模拟效果可由提升速度v表示,所以模拟时忽略Q的影响;层间距L的影响见图6,从图中可知,罐道连接的部位会引起力的突变,但不会影响水平力的变化规律及其最大值,所以模拟中不考虑L的影响;C主要受L的影响,暂不做模拟;δ模拟难度很大且本身不具有规律性,暂不考虑;结合FLUENT软件的特点,模拟中仅考虑v和Fa的影响。
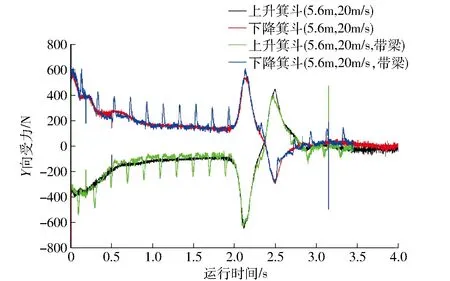
图6 罐道梁对水平力的影响图
初步模拟可知,箕斗受到的水平荷载,除在相遇的50m范围内存在较大波动外,其余均平稳运行,因此井筒建模范围取100m,模拟参数见表2。

表2 数值模拟参数表
4.2 建模
箕斗实际模型总网格数为600万~700万个,见图7。
4.3 箕斗运行状态模拟
箕斗相遇过程的受力状态见图8~图11(井筒直径5.6m,提升速度20m/s),箕斗在相遇过程中活塞风有增大的趋势,在远离过程中活塞风有减小的趋势,但总体过渡平稳。

图8 箕斗相遇过程图

图9 箕斗运行中Y向受力变化曲线
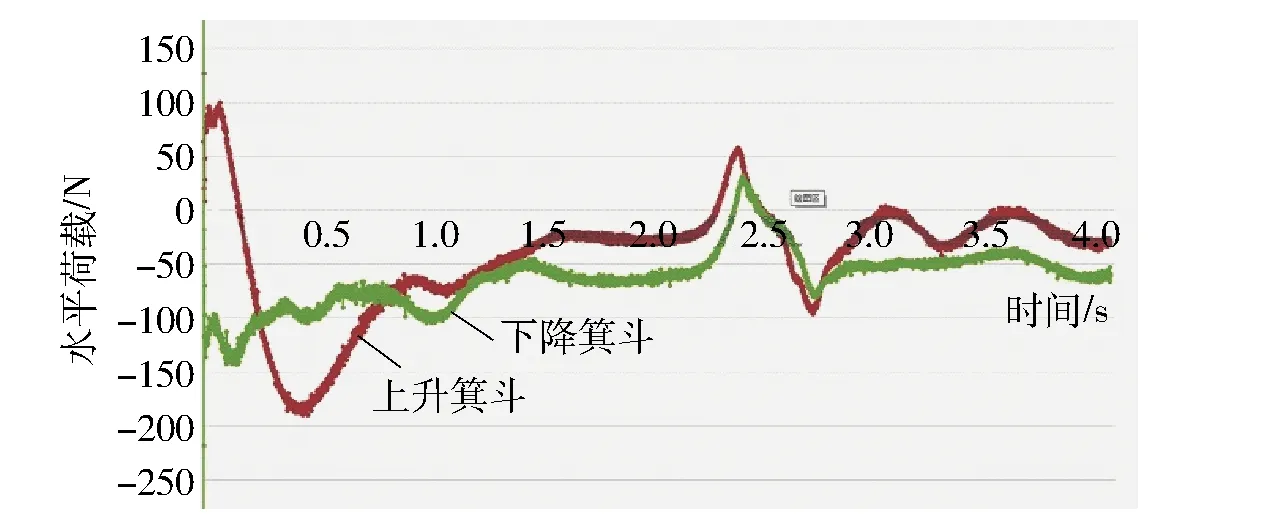
图10 箕斗运行中X向受力变化曲线
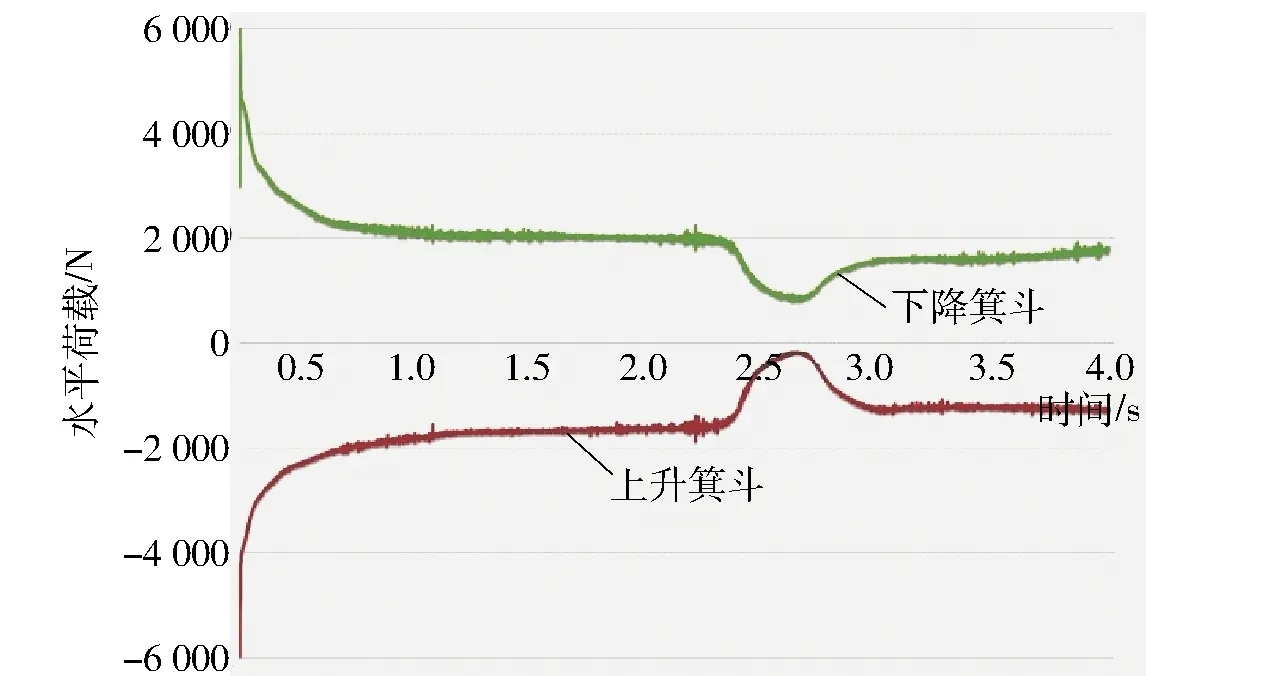
图11 箕斗运行中Z向受力变化曲线
箕斗相遇时在X、Y和Z3个方向上均有力的突变(X、Y和Z的方向示意见图1),该力在X向和Y向上有瞬间的增加,设备之间形成推力,最大为600N;该力在Z向上有瞬间的减小,设备之间形成吸力,该值从6 000N减小到200N,Z向力主要是设备运行时产生的风阻力,对钢罐道水平荷载Fh的影响较小。因此空气动力Fa对水平力的影响很小。
(1)提升速度的影响。提升速度越大风阻越大,水平力也越大,提升速度与水平力为正线性相关,但总体影响较小,见图12和图13。
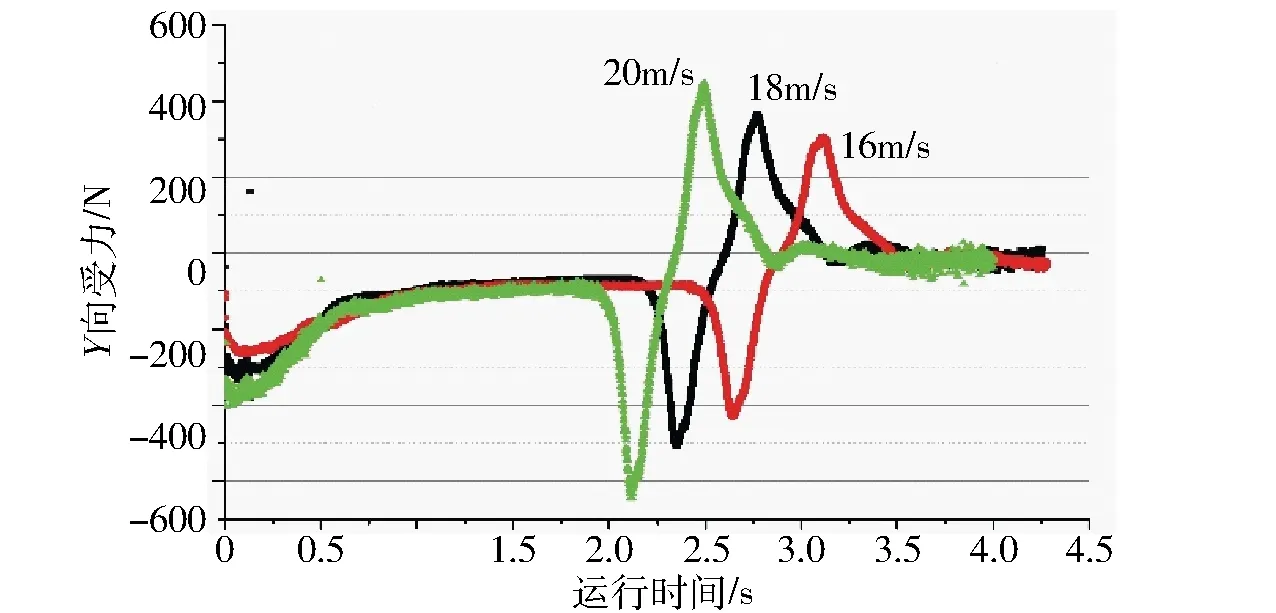
图12 不同速度Y向受力变化曲线(井筒直径5.6m)
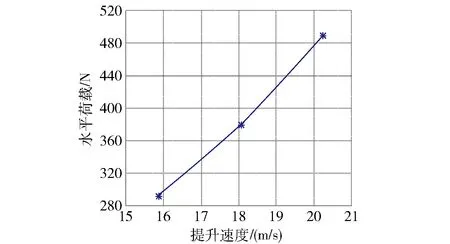
图13 提升速度与水平力关系曲线
(2)井筒直径的影响。箕斗所占井筒面积比越大,箕斗受到空气动力的影响越大,见图14,但该因素的影响很小。
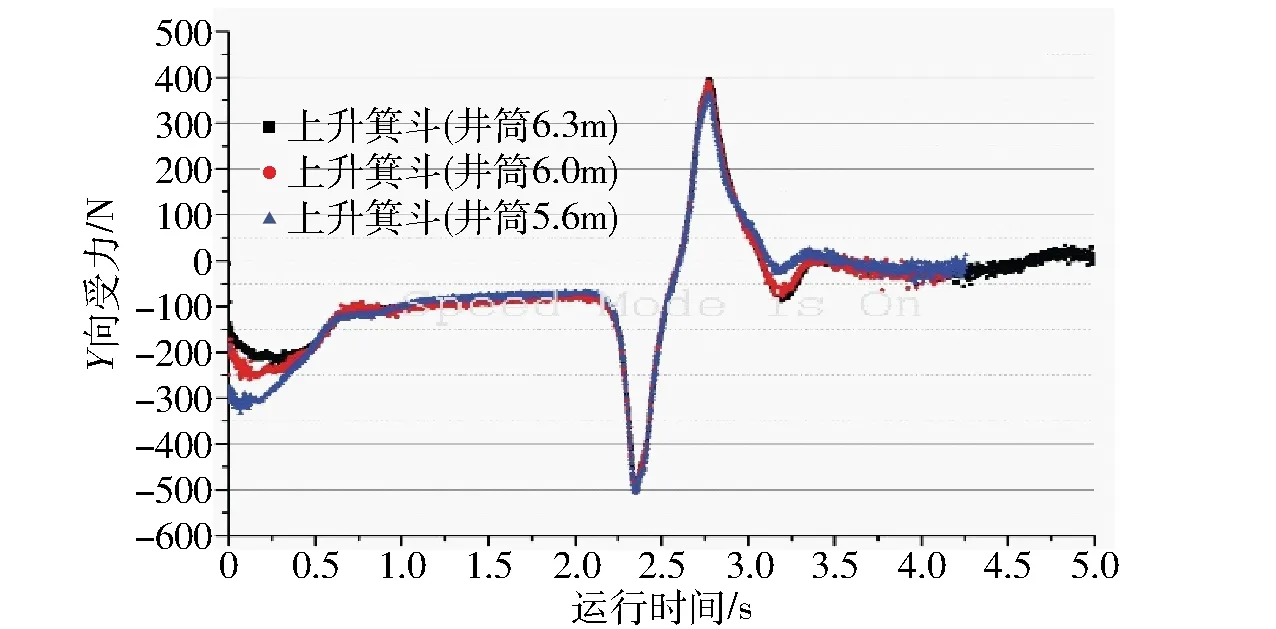
图14 不同井筒直径Y向受力变化曲线(箕斗运行速度18m/s)
通过模拟可以看出,作用于提升容器的空气动力主要与容器的外形和提升速度有关,受井筒面积和罐道层间距的影响较小;同时,空气动力引起的水平荷载较小且为瞬时荷载,在井筒装备设计中可不予考虑。
5 小结
综上所述,罐道正面水平力Fh受多种因素的影响,且具有一定的随机性,归纳起来Fh可用以下函数表示:
Fh=f(Q,v,L,δ,C,Fj)
式中:Fh——提升容器运行时的正面水平力,kN;
Q——提升终端荷重,kN;
v——提升速度,m/s;
L——罐道梁层间距,m;
δ——安装偏差,mm;
C——井筒装备的整体刚度,在具体的公式中有不同的表达方式;
Fj——滚轮罐耳预压,N。
国内外不同的计算公式虽然在表现形式上有所不同,但不会脱离上述函数表达式的范围。同时考虑到公式的实际应用,以及各影响因素之间的相互关系,上述函数也可以简化为Fh=f(Q,v,L,δ)。
6 结语
多年来,设计中一直采用经验公式对钢罐道的水平力进行计算,但这些公式只适用于井筒深度较浅、终端荷载和提升速度较小的情况,当外部环境发生较大变化时,水平力的计算超出了经验公式的使用范围,该公式不能满足井筒深度更大、提升速度更快和终端荷载更重的情况。本文通过分析、FLUNT模拟等手段,对可能影响钢罐道水平力的多种因素进行了研究,给出了科学、合理的钢罐道正面水平力计算函数,可供相关从业者借鉴和探讨。
[1] 张荣立,何国伟,李 铎.采矿工程设计手册(中册)[M].北京:煤炭工业出版社,2003.
[2] 《采矿设计手册》编委会.采矿设计手册·井巷工程卷[M].北京:中国建筑工业出版社,1989.
[3] 史天生,田建胜,郭晋蒲.刚性井筒装备水平作用力的研究[J].煤炭学报,1993,(6).
[4] 史天生,王东权,刘志强.深立井刚性井筒装备的发展与展望[J].煤炭设计,1997,(12).
[5] [苏]H.K 沙弗拉诺夫.立井井筒安装工艺[M].北京:煤炭工业出版社,1987.
[6] SANS 10208- 4:2011,South African National Standard[S].Design of structure for the mining industry,Part 4:Shaft system structures. SABS Standards Division.2011.
[7] AS/NZS 3785.6:2015,Australian/New Zealand Standard[S].Underground mining-Shaft equipment,Part 6:Fixed guides,rope guides and rubbing ropes for conveyances. Joint Technical Committee ME- 018,Mining Equipment.15 April 2015.
[8] KRIGE G J.Some initial findings on the behavior and design of mine-shaft steelwork and conveyances[J].J.S.Afr.Inst.Min.Metall.,1986,86(6):205-215.
[9] SME Mining Engineering Handbook[M].Society for Mining,Metallurgyand Exploration,Inc.,December,1996:1651-1672.
Influence factors analysis of steel guide load system in shaft
Horizontal load of steel guide in vertical shaft is impacted by kinds of factors, commonly used an empirical formula in designing. With the development of speed and depth higher in shaft, the empirical formula can’t satisfy the engineering requirement. As for, in this paper sorts of factors might affect guide horizontal load was analyzed, especially a simulation software FLUENT was used to simulate the impact of aerodynamic. In the end a universal function is given, which can provide reference for the designer.
horizontal load; influence factors; simulation software; universal function
1672-609X(2017)05-0054-06
TD531
A
王建中(1980-),男,山西大同人,高级工程师,从事金属矿山井巷工程及岩土工程的相关咨询设计、科研工作。

