Y型微通道中压力驱动幂律流的流动分离
郭松灿,朱庆勇,陈耀钦
(中山大学应用力学与工程系, 广东 广州 510275)
Y型微通道中压力驱动幂律流的流动分离
郭松灿,朱庆勇,陈耀钦
(中山大学应用力学与工程系, 广东 广州 510275)
基于Poisson-Boltzmann方程、修正的Cauchy动量方程和流体连续性方程,对压力驱动下的幂律流在Y型微通道中的流动过程进行了数值模拟。分析了不同的幂律指数、压强差下双电层电场、速度场的分布,以及双电层对速度场的影响。计算结果表明:① 在Y型微通道的某些位置会发生流动分离(回流);② 发生回流时的临界压强差和分叉角关系曲线表明:增大分叉角或降低幂律指数可使临界压强差下降;③ 幂律指数越小,双电层影响越明显;④ 增大压强差、降低幂律指数和增大分叉角度,均可使回流区域变大。
Y型微通道;幂律流体;双电层;回流
固体壁面与电解质溶液接触时,壁面会发生电离而带电并产生壁面电位势,从而使溶液中同种电荷受到排斥,异种电荷受到吸引聚集到壁面附近。固体壁面附近的带电液体薄层即为双电层[1]。双电层厚度极小,一般只有几百纳米。在宏观流动中,双电层作用可以忽略。而在微通道内,双电层对流动的影响却不容忽视。这是因为在压强差的作用下,流体会与带电颗粒一起运动,形成电流。流动的电荷随即在微通道内诱导出一个电位差(流动电位势)[2],电荷因流动电位势的作用而受到一个与运动方向相反的电场力。流动电位势的作用效果与增大流体黏性相似,所以这种现象被称为双电层的电黏性效应[3]。
早有学者研究了双电层作用下的流体在无限长等截面微通道中的流动。Li[4]研究了矩形微流道内流体流动的机理,得到关于二维流动的解析解。Wu等[5-7]研究了无限长平行板微流道中各种复杂边界条件下牛顿流体的流动特性,并给出了相应的解析解。工业中大部分的流体并不是牛顿流体,如橡胶溶液、工程塑料等[8],仅研究牛顿流体的微流动不能完全满足实际需要。随后,Jian等[9-11]研究了在矩形、圆形截面等微通道中的非牛顿流体的流动及传热特性。Zhu等[12]研究了矩形微通道内受周期性压力驱动的幂律流体的流动特性,发现:幂律指数影响流体在微通道内的速度分布,且幂律指数越小双电层作用越明显。与此同时,更接近实际情况的复杂微通道内的流体流动研究也在不断开展。例如,段娟等[13]探讨了微扩张管道内幂律流体非定常电渗流动,给出了恒定电场下流场随时间的变化情况。龚磊等[14]模拟了微扩散通道中的压力驱动流,给出了从瞬态到稳态的发展过程中流动电位势和流场的变化,并对电黏性作出了分析。也有学者对更为复杂的微通道内的流体流动进行模拟,如T型微混合器等[15]。但少有学者深入研究非牛顿流体在复杂微通道中的流动特性。
因此,本文选取平面Y型通道作为几何模型,结合双电层电黏性和幂律流体本构关系,讨论了Y型微通道内回流产生的临界条件,及回流区域大小与各参数间的关系。研究结果揭示了非牛顿流体在Y型微流道中的流动机理,对工程和实际应用都有重要的意义。
1 物理和数学模型
1.1 物理模型
本文的研究对象为二维Y型微通道,其结构如图1所示。
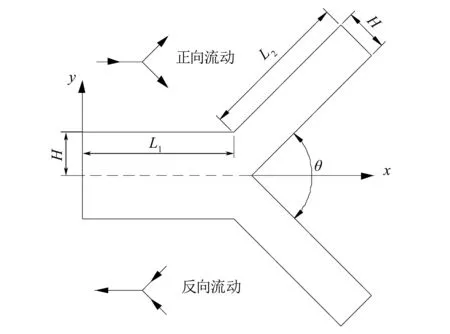
图1 Y型微通道模型Fig.1 Y-shaped microchannel model
如图所示,θ为两分支通道的夹角(分叉角)。计算模型中,假设两分支通道与主通道夹角相等。若流体从主通道向分支通道流动,则称为正向流动;反之称为反向流动。流动方向不同,流体所受到的阻力不同,并产生不一样的流场。
1.2 数学模型
幂律流体的本构模型如下[16]:
τij=-pδij+2μaDij
(1)
其中τij为应力张量,p为压力,δij为单位张量,即
Dij为速度变形张量,μa为表观黏度。在二维平面流动中,Dij和μa定义如下:
(2)

(3)
式中n为幂律指数,是无量纲量。μ0为稠度系数,量纲为N·sn/m2。显然,当n=1时,μa为常数,流体为一般牛顿流体;n<1时流体呈剪切变稀,n>1时流体呈剪切变稠。将幂律流体本构关系代入动量方程中,忽略电场力以外的体积力。因此,流体控制方程如下:

(4)
(5)
其中,(4)式为二维不可压缩流体连续性方程。ρ为流体密度, (5)式最后一项为作用于流体的电场力,其作用方向总与流体运动方向相反,表现为流动附加阻力。双电层电位势以及电荷体积密度满足Poisson-Boltzmann方程[17]:
(6)

(7)
其中,ψ为双电层电位势,ρe为电荷体积密度,ε为溶液介电常数,n∞表示不受双电层影响处单位体积所含离子个数,z为溶液离子价,kb是Boltzmann常数,T为绝对温度,e为电子电荷量。式中F=Eρe,E为微通道内流动电场强度。根据电流密度平衡条件[18],E应满足:

(8)
式中,λ为微通道总电导率。所以:
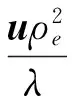
(9)
1.3 控制方程的无量纲化和边界条件
为了便于计算,将控制方程进行无量纲化,即引入以下无量纲量
(10)

(11)
(12)

(13)
速度和电势场在进出口取第二类边界条件,压力在进出口取第一类边界条件,通道壁面处取无边界滑移条件,对称边JH取对称边界条件。(11)、(12)式的边界条件为:
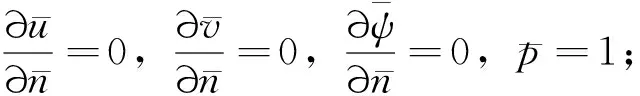
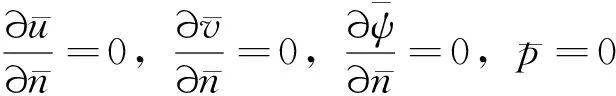
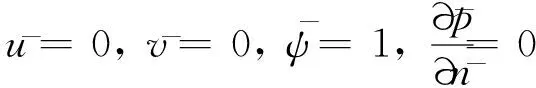
2 数值分析
2.1 数值离散
本文所研究几何模型具有对称性,在Re数不太大的情况下,流动也具有对称性。故取主通道中线为对称轴,仅对上半部分进行计算分析,计算区域如图2所示。时间方向上,采用三阶Runge-Kutta法离散。空间方向上,使用边界拟合坐标,将物理平面上的网格变换到计算平面中的规则矩形网格,其网格步长为1。采用四阶紧致差分格式进行离散[19]:
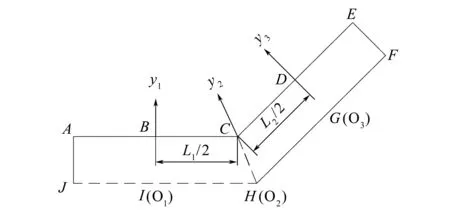
图2 计算区域Fig.2 Computational domain
(14)
(15)
其中,算子I满足:
Imf(x)=f(x+mΔx)
(16)
而,Fi(f),Fj(f)为一阶偏导的差分逼近,Si(f),Sj(f)为二阶偏导的差分逼近,下标i,j分别表示水平方向第i节点和竖直方向第j节点,f表示式(11)、(12),中的
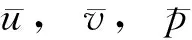
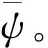
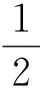
(17)

(18)
S1(f)=2f1-5f2+4f3-f4
(19)
Sn(f)=2fn-5fn-1+4fn-2-fn-3
(20)
(18)、(20)式中各项的下标表示一行(列)中的节点号,n为一行(列)中最后一个的节点的节点号。(11)式的半离散形式为:
(21)
其中




(12)式半离散形式为:
(22)
部分文献对方程(12)右端的源项进行线性化处理,这使得在Zeta电位较大时误差明显。为扩大动量方程适用范围,本文求解式源项采用以下格式[21]:
sinh(φk+1)=sinh(φk)+(φk+1-φk)cosh(φk)
(23)
2.2 数值模拟结果
[12,18,22],本文各算例中的参数取值如表1所示。正向流动时,Δp取正值;反向流动时,Δp取负值。

表1 计算中各参数取值Table 1 Value of parameters used for simulation
2.2.1 模型验证 将分叉角设为0°,HF边设为对称边,本文模型即为二维均匀微通道内的流动。文献[5]中给出了对应的牛顿流体的解析解。EF边的模拟结果与文献[5]中解析解如图3所示,其中横坐标表示CH截面的无量纲高度,纵坐标表示沿水平方向的无量纲速度。可以看出,模拟结果与解析解高度吻合,模拟算法是有效的。
2.2.2 双电层电势场 图4为无量纲双电层电势在计算区域内的分布图。在本文所选取的数学模型中,双电层电势依赖于求解式,与其它流体参数无关。电势沿通道径向变化快慢依赖于κH,本文取κH=32。如图4所示,在壁面附近电势迅速变化,在计算区域的其它位置,电势几乎不变化,符合双电层理论假设。

图3 牛顿流体数值解与解析解对比Fig.3 Results comparison of the numerical of Newtonian fluid with the analytical solution
2.2.3 不同幂律指数下的流动特性 图5给出牛顿流体在Y型微通道中的流线图,其中背景色表示速度值的大小。如图5表明:相同的压差(|Δp|=100 Pa)下,幂律指数不同或流动方向不同时,呈现不同的流动形态。基于幂律流体的本构关系,n>1(胀流型流体)流体剪切率越高表观黏度越高;n<1(拟塑性流体)流体剪切率越高表观黏度越低。且,相同条件下,胀流型流体受到壁面的粘性力作用较大。从图5的(c)和(d)可以看出,胀流型流体在远离分叉处的流动基本与壁面平行;在分叉处附近的速度等值线轮廓较为相似。与之相反,相同条件下拟塑性流体受到较小的壁面粘性力,受壁面的约束能力较弱,所以有较高的速度峰值并且容易产生涡结构,如图5(b)所示。由于正向流动中FH边提供阻力,可有效约束在分叉点后的流体流动。同时,由于流体会保持原有的惯性,使得分支通道中轴线偏H点一侧的平均流速大于偏C点一侧的平均流速。在反向流动中,JH边为对称边界,在下游不提供壁面粘性力约束流体流动。所以,相同情况下H点附近和C点下游的区域更容易产生回流,如图5(b)所示。
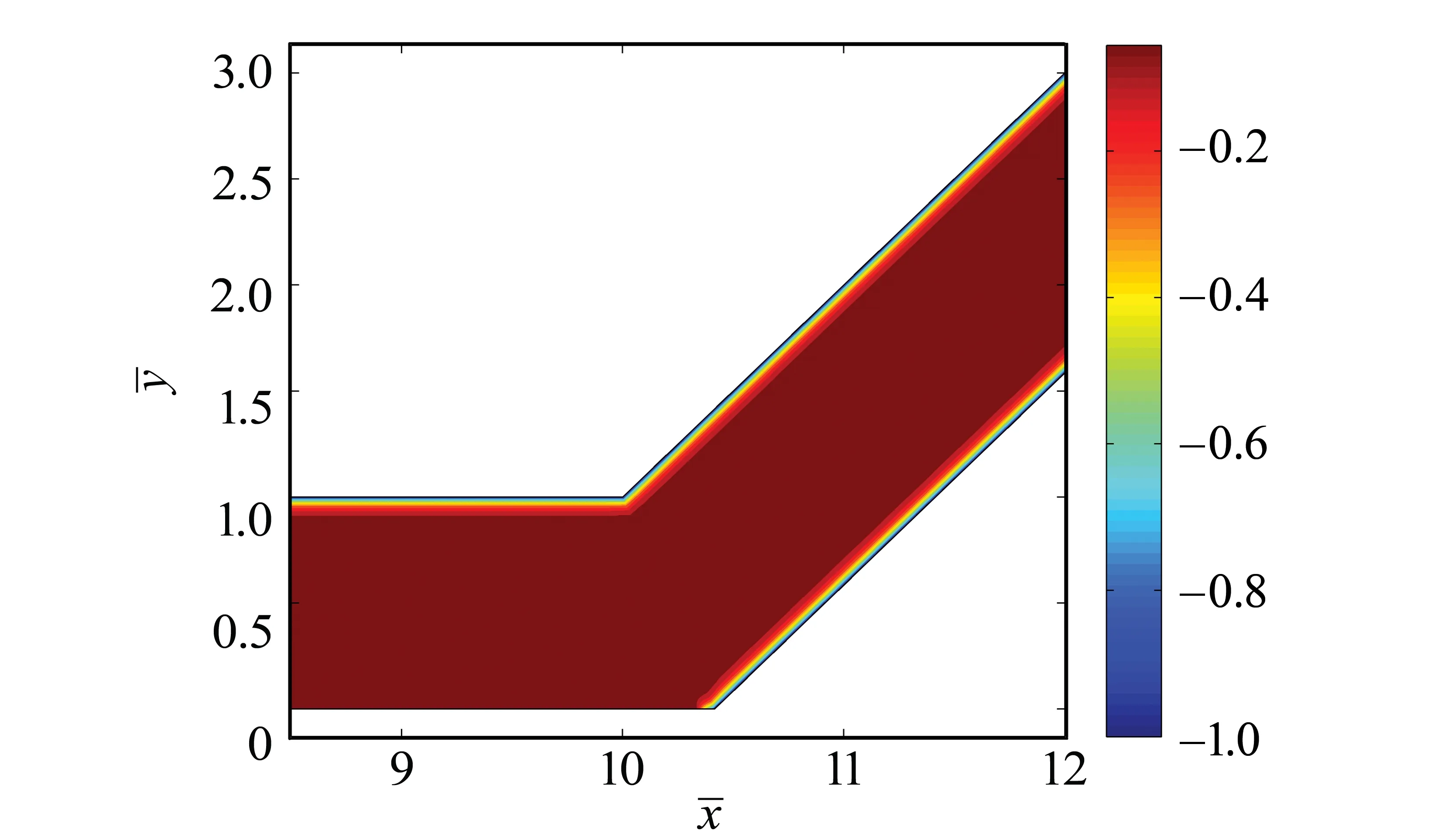
图4 双电层无量纲电势场Fig.4 Dimensionless potential of electric double layer

图5 不同幂律指数和流动方向的流线图Fig.5 Streamline of different power-law index and the flow direction
图6为n=0.8和n=1.2的幂律流体正(反)向流动的无量纲表观黏度分布图。在计算区域中,主通道与分支通道截面积相同,流体不可压缩,结合流体连续性可知,主通道和分支通道的截面平均流速相同。但是分支通道有两侧边界提供壁面约束流动(壁面上流速为零),而主通道只有一侧,所以一般情况下分支通道内流体剪切率比主通道的大。剪切率最大的位置并不在通道壁上。如图6中的 (a)和(c)所示,壁面附近,由于有双电层作用,降低壁面附近流速,导致壁面附近的流体剪切率较低。离开双电层后,速度迅速变大,流体剪切率达最大值。对比图5 (b)和图6 (b),可以看出:涡结构附近流速较低、有较低的剪切率,所以在拟塑性流体的黏度分布图中表现为获得较大的表观黏度。图6中的(c)和(d)黏度等值线的轮廓相似度较高,表明胀流型流体流动受壁面约束作用明显,在低压(|Δp|=100 Pa)状态下,正向、反向流动有相似的速度等值线,所引起的流体剪切率分布几乎相同。

图6 无量纲表观黏度Fig.6 Dimensionless apparent viscosity
压强差是流体流动的主要因素。进出口压差相反,则流动方向相反。图7给出不同幂律指数下,正(反)方向流动的无量纲压强分布。在分支通道有两边壁面提供流动阻力,而在主通道只有一边提供流动阻力。所以分支通道的压力梯度比主通道的大,这在胀流型流体中尤为明显,如图7(c)和(d)所示。由于流体动量的作用,在H点产生了局部的高压;同时,由于流体保持其原有流动惯性,在C点及C点下游产生了局部的低压。这在拟塑性流体中尤为明显,如图7(a)和(b)所示。所以,相同条件下,惯性力对拟塑性流体的作用比胀流型流体要显著;粘性力对胀流型流体作用比拟塑性流体要显著。对比图7的(c)和(d),可以看出:胀流型流体在远离分叉处的压强等值线几乎相互平行。这说明:在该条件下,流体受粘性力显著,表现为层流流动。
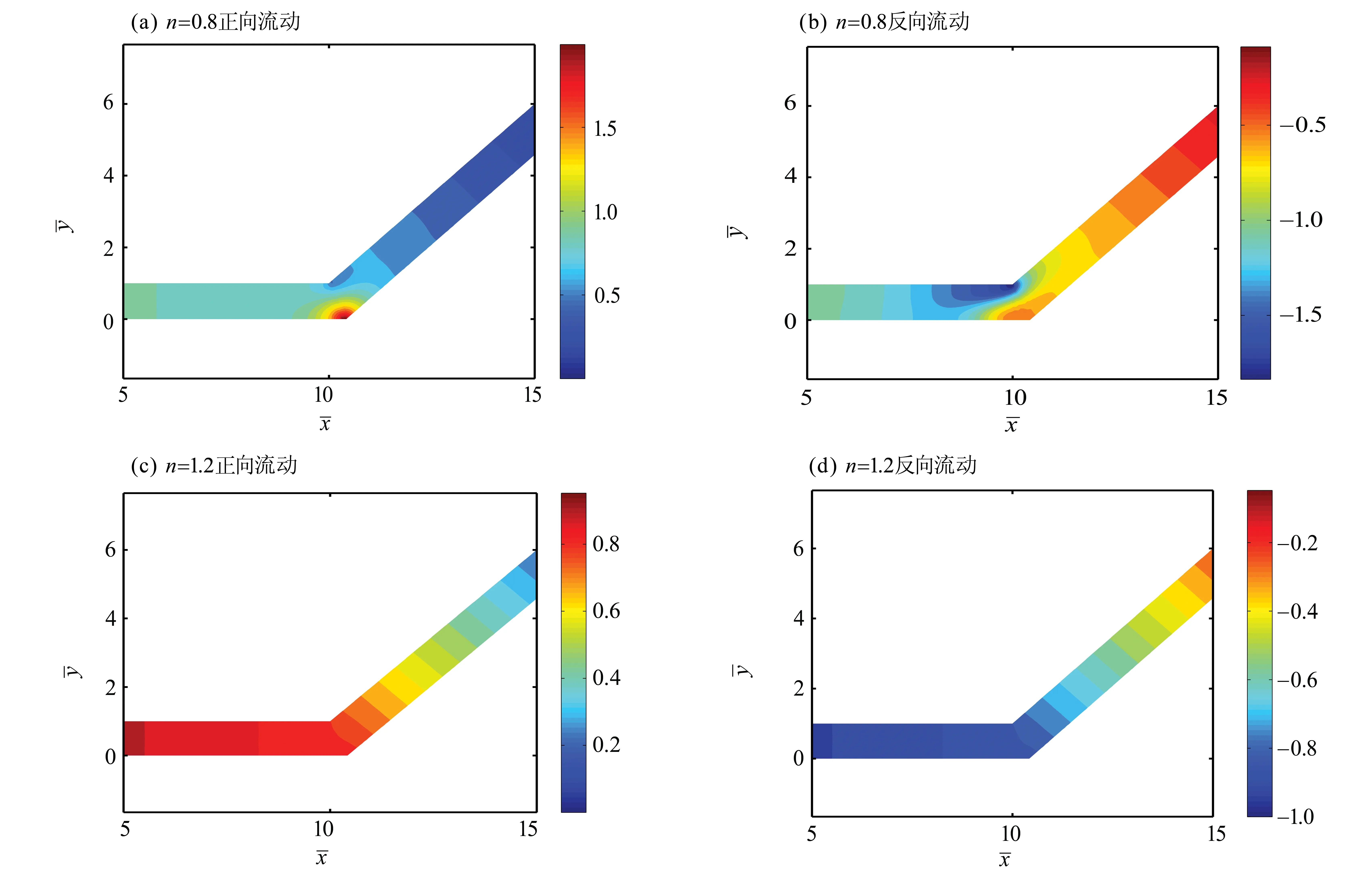
图7 无量纲压强Fig.7 Dimensionless pressure

如图8所示,由于双电层的作用,考虑双电层时的整体速度相对于无双电层时的整体速度有所减小。拟塑性流体受粘性阻力作用较小,其可获得较高速度峰值。从而受较大的电场力,所以拟塑性流体的双电层作用尤为明显。与之相反,在本文算例中胀流型流体所获得的速度较低、受到的电场力极小,在所选取的观察截面中双电层作用并不十分明显。这与文献[12]的结论相符。本文基于无壁面滑移假设进行模拟,结合(9)式可知,在壁面处电场力为零。所以本文计算结果中,如图8(d),未出现采用截面均匀流动电位势所致的非物理的局部回流现象,与文献[18]结论相符。结合图8(a)、图8(b)和图5(b)分析拟塑性流体反向流动,在H点附近发生回流,且在回流区域中流速较低。
2.2.5 各参数对回流区域的影响 在一定条件下,C点下游和H点附近会产生回流涡。下面讨论产生回流的临界条件,以及幂律指数、压强差和分叉角对回流区域大小的影响。
1) 产生回流的临界条件。观察流场时,根据各节点速度方向判断是否发生回流。将各节点速度投影至其最近的壁面上,若平行于壁面的速度分量与微通道内主要流动方向相反,则认为发生回流。计算结果表明,一般情况下,在三处发生回流,分别为:正向流动CD附近、反向流动BC附近、反向流动H点附近。获得各组临界压强后,对数据进行回归分析。正向流动使用幂函数模型,反向流动使用指数模型,效果较好。计算结果如图9,圆点为数值结果,曲线为对应的拟合结果。
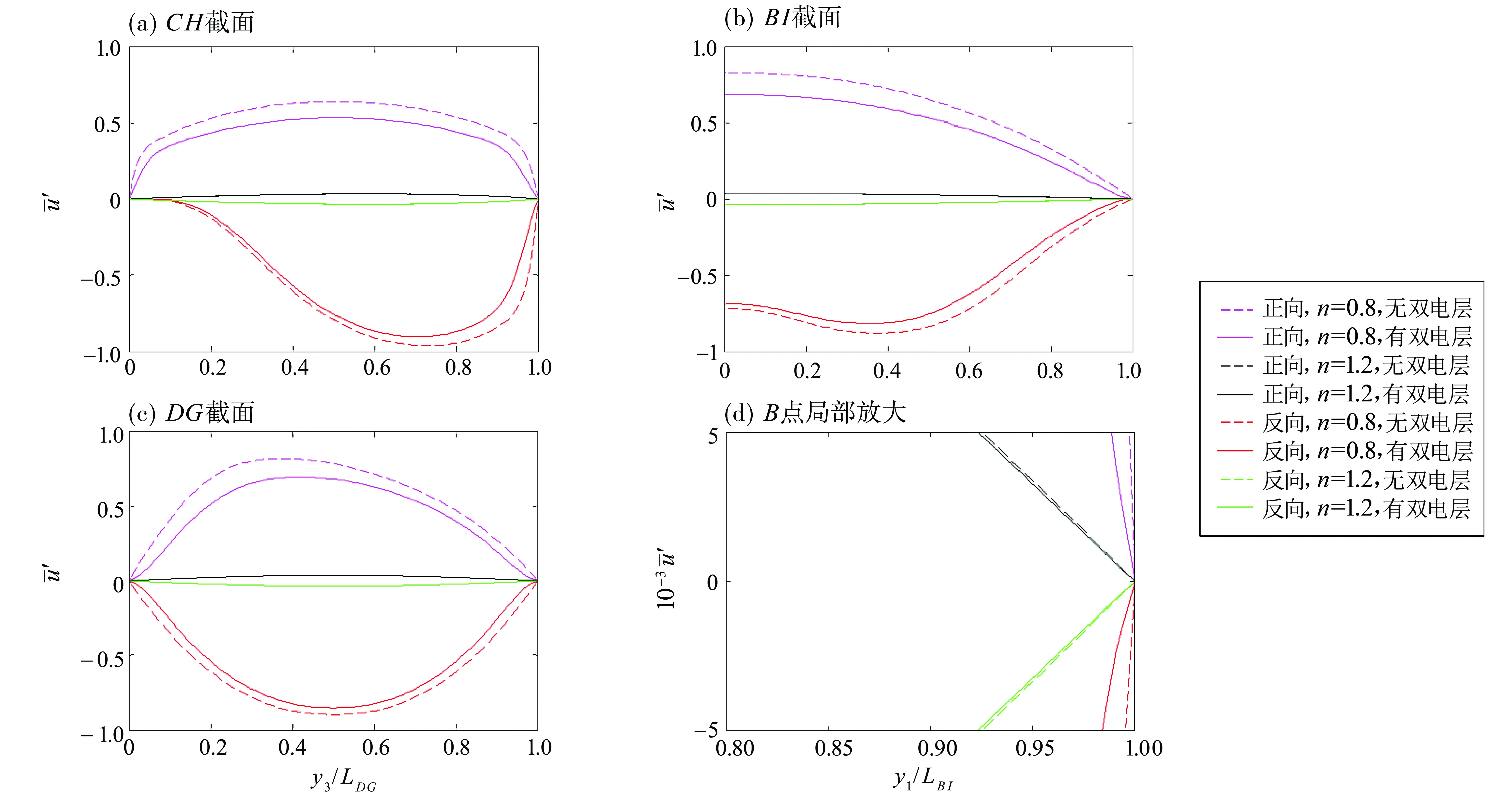
图8 不同幂律指数下不同截面的无量纲速度轮廓Fig.8 Dimensionless velocity profiles of different power-law index and different section (a) section C-H; (b) section B-I; (c) section D-G; (d) detail view of point B

图9 分叉角与发生回流的临界压强的变化曲线Fig.9 Branching angle and the vortex generating critical pressure (a) normal flow, nearby CD; (b) reversed flow, nearby BC; (c) reversed flow, nearby point H
流动分离主要由惯性力、粘性力和压强梯度共同作用产生。在C点上游,流体的惯性力与压强梯度共同克服流体的粘性力,使流体顺利地沿固壁往下流动。流体进入逆压区,惯性力要克服粘性力和逆压强,惯性力不足时流体就会回流。从图9可以看出,幂律指数越小越“容易”产生回流(相同条件下,产生回流所需的临界压差较低),幂律指数越大越“不容易”产生回流(相同条件下,产生回流所需的临界压差较高)。
当分叉角变大时,流动方向改变的角度变大,C点下游附近平行于壁面的速度分量越小,即惯性力平行于壁面方向的分量越小,同时由于流体动量的作用,逆压区变大。惯性力不足以克服粘性力和逆压强。所以分叉角越大,越“容易”发生回流。分叉角变小,惯性力在壁面方向的分量迅速变大,同时由于流体动量分布不均匀引起的逆压区迅速变小,导致发生回流所需压强差急剧上升。
主通道宽度较大,导致主通道中流动的Re数较大,并且电黏性影响较小;相反分支通道宽度较小,流动Re数较小,并且电黏性影响较大。所以如图9(a)和(b),反向流动更“容易”发生回流。H点附近回流涡的鞍点在H点的下游一侧对称边上,该点的剪切应力为零。把无阻力边设置在H点下游一侧,是H点附近发生回流的有利条件,所以正向流动时在H点附近一般不发生回流。对比图9的(b)和(c),可以看出:一般情况下,BC附近比H点附近更“容易”发生回流。
2)回流区域的大小。为方便探究回流区域的大小,记流动分离的再附点为S点。在S点上,流体对壁面的剪切力为零,在垂直于壁面的方向上速度梯度为零。根据边界附近节点的速度,使用线性插值的方式近似地找出S点的位置。进一步求出S点与C点的无量纲距离,记为LS,用来衡量回流区域的大小。n和θ分别取(0.97,110°),(1.00,110°),(1.00,120°),(1.03,120°),在适当的压强差下求出LS,计算结果如图10所示。

图10 不同参数下回流区域的大小Fig.10 Size of vortex regions with different parameters (a) normal flow; (b) reversed flow
图10显示,回流区域的大小与压强差正相关。且在一定的压强差范围内,回流区域的大小随压强差线性增长,其变化率与n和θ的取值有关。对比图10的(a)和 (b),要获得大小相近的逆压区,反向流动所需要的压力差较小。对比n和θ取(1.00,110°),(1.00,120°)时的数据,发现:在适当的范围内增大分叉角,可使回流区域变大,与减小幂律指数的效果相似。进一步比较n和θ取(0.97,110°),(1.00,110°),(1.00,120°)时的三组数据,可以看出:在一定范围内,回流区域的大小对幂律指数的变化较为敏感。综上所述,减小幂律指数、增大压强差或增大分叉角均能使回流区域变大。
3 结 论
本文研究了压力驱动下幂律流体在Y型微通道中的流动,并讨论了微通道的某些位置发生回流的条件,回流区域大小的变化趋势以及影响回流区域大小因素。研究结果对于工业中的微流控芯片的设计与生产有一定指导意义。主要结论如下:
1)相同条件下,拟塑性流体获得较低的表观黏度,流速峰值较高,受双电层影响较大;胀流型流体获得较高的表观黏度,流速峰值较低,受双电层影响较小。牛顿流体表现介于两者之间。幂律指数越小,流场对各参数的影响越敏感。
2)反向流动比正向流动更“容易”产生回流。相同条件下,若都产生回流,反向流动的回流区域较大。
3)分叉角减小到一定的程度,产生回流所需的压力差(临界压差)将急剧上升。正向流动时,分叉角和临界压差呈幂函数关系;反向流动时,分叉角和临界压强呈指数函数关系。
4)其它条件不变的前提下,单一增大压强差、减少幂律指数或变大分叉角度,若未发生回流则能促进回流的产生,若已发生回流则可使回流区域变大。在一定范围内,压强差与回流区域大小之间呈线性正相关。
参考文献:
[1] LI D Q. Electrokinetics in microfluidics[M]. New York: Elsevier, 2004: 1-10.
[2] HUNTER R J. Zeta potential in colloid science [M]. London: Academic Press, 1981: 11-58.
[3] YANG C, LI D Q, MASLIYAH J H. Modeling forced liquid convection in rectangular microchannels with electrokinetic effects[J]. International Journal of Heat and Mass Transfer, 1998, 41(24):4229-4249.
[4] LI D Q. Electro-viscous effects on pressure-driven liquid flow in microchannels[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2001, 195(1): 35-57.
[5] GONG Lei, WU Jiankang, WANG L, et al. Streaming potential and electroviscous effects in periodical pressure-driven microchannel flow[J]. Physics of Fluids (1994-present), 2008, 20(6): 063603.1-063603.7.
[6] WANG Lei, WU Jiankang. Periodical pressure-driven flows in microchannel with wall slip velocity and electro-viscous effects[J]. 水动力学研究与进展B辑, 2010, 22(6): 829-837.
[7] WANG Lei, WU Jiankang. Flow behavior in microchannel made of different materials with wall slip velocity and electro-viscous effects[J]. Acta Mechanica Sinica, 2010(1): 73-80.
[8] 陶友季,章自寿,麦堪成. PP/回收PET共混物的动态流变行为[J]. 中山大学学报(自然科学版),2010, 49(1): 62-66.
TAO Youji, ZHANG Zishou, MAI Kancheng. Dynamic rheological behaviours of polypropylene/recycled poly(ethylene terephthalate) blends[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010, 49(1): 62-66.
[9] WANG Lin, JIAN Yongjun, LIU Quansheng, et al. Electromagnetohydrodynamic flow and heat transfer of third grade fluids between two micro-parallel plates[J]. Colloids and Surfaces A Physicochemical and Engineering Aspects, 2016(494): 87-94.
[10] ZHAO Guangpu, JIAN Yongjun, LI Fenqing. Heat transfer of nanofluids in microtubes under the effects of streaming potential[J]. Applied Thermal Engineering, 2016(100): 1299-1307.
[11] ZHAO Guangpu, JIAN Yongjun, LI Fenqing. Streaming potential and heat transfer of nanofluids in parallel plate microchannels[J]. Colloids and Surfaces A Physicochemical and Engineering Aspects, 2016(498): 239-247.
[12] ZHU Qingyong, DENG Shuyan, CHEN Yaoqin. Periodical pressure-driven electrokinetic flow of power-law fluids through a rectangular microchannel[J]. Journal of Non-Newtonian Fluid Mechanics, 2014(203): 38-50.
[13] 段娟,陈耀钦,朱庆勇. 微扩张管道内幂律流体非定常电渗流动[J]. 物理学报, 2016, 65(3): 162-174.
DUAN Juan, CHEN Yaoqing, ZHU Qingyong. Electroosmotically-driven flow of power-law fluid in a micro-diffuser[J]. Acta Physica Sinica, 2016, 65(3): 162-174.
[14] 龚磊,吴健康. 微扩散通道中的流动电位势和电黏性效应分析[J]. 微纳电子技术, 2007, 44(6): 312-318.
GONG Lei, WU Jiankang. Analysis on streaming potential and electro-viscous effect in a micro-diffuser[J]. Micronanoelectronic Technology, 2007, 44(6): 312-318.
[15] EBRAHIMI S, HASANZADEH-BARFOROUSHI A, NEJAT A, et al. Numerical study of mixing and heat transfer in mixed electroosmotic/pressure driven flow through T-shaped microchannels[J]. International Journal of Heat and Mass Transfer, 2014, 75: 565-580.
[16] 陈文芳,蔡扶时. 非牛顿流体的一些本构方程[J]. 力学学报,1983, 19(1): 18-28.
CHEN Wenfang, CAI Fushi. Some constitutive equations for non-newtonian fluids[J]. Acta Mechanica Sinica, 1983, 19(1): 18-28.
[17] DUTTA P, BESKOK A, WARBURTON T C. Numerical simulation of mixed electroosmotic/pressure driven microflows[J]. Numerical Heat Transfer, Part A: Applications, 2002, 41(2): 131-148.
[18] 龚磊,吴健康. 微通道液体流动双电层阻力效应[J]. 应用数学和力学, 2006, 27(10): 1219-1225.
GONG Lei, WU Jiankang. Resistance effect of electric double layer on liquid flow in microchannel[J]. Applied Mathematics and Mechanics, 2006, 27(10): 1219-1225.
[19] 马延文,傅德薰. 紧致格式数值模拟超音速粘性绕流问题[J]. 空气动力学学报, 1988(3): 365-369.
MA Yanwen, FU Dexun. Numerical simulation of compact schemes in super-sonic viscous flows[J]. Acta Aerodynamica Sinica, 1988(3): 365-369.
[20] ZHU Qingyong, ZHANG Dingling, DENG Shuyan, et al. High order compact difference schemes for the complex flow fields in anisotropic porous fibrous media with sorption[J]. Computers and Fluids, 2013, 88: 473-483.
[21] PATANKAR S V. Numerical heat transfer and fluid flow[M]. New York: McGraw-Hill, 1980: 161-174.
[22] MANSOURI A, VALI A, KOSTIUK L W. Electrokinetic power generation of non-Newtonian fluids in a finite length microchannel[J]. Microfluidics and Nanofluidics, 2016, 20(5): 1-13.
Flowseparationofthepressuredrivenpower-lawflowinY-shapedmicrochannel
GUOSongcan,ZHUQingyong,CHENYaoqin
(Department of Applied Mechanics and Engineering, Sun Yat-sen University,Guangzhou 510275,China
The pressure driven flow of power-law fluids in Y-shape microchannel is calculated by the fourth-order compact difference scheme. The governing equations are established by the complete Poisson-Boltzmann equation, modified Cauchy momentum equation and continuity equation. The distribution of the electric double layer potential, the pressure, the apparent viscosity and the velocity profiles of different parameters are obtained by the simulation. The results of the simulation are discussed. Furthermore, the effects of the electric double layer on the velocity profile were investigated. The results show that with the decrease of the power-law index, the velocity peak of the flow is larger in the microchannel, the effects of the electric double layer are more obvious. Compared the shear thickening and Newtonian fluids, the shear thinning fluids are much more sensitive to the other parameters. The recirculation generating conditions are studied. The recirculation generating critical pressure decrease with enlarging the branching angle or decreasing the power-law index. The pressure, the power-law index and the branching angle have significant influence on the flow separation when fixing the other parameters. Increasing the pressure, decreasing the power-law index or enlarging the branching angle also can extend the region of the flow separation.
Y-shaped microchannel; power-law fluid; electric double layer; backflow
O357.1
A
0529-6579(2017)05-0139-10
10.13471/j.cnki.acta.snus.2017.05.018
2017-01-03
国家自然科学基金重大研究计划(91230114); 地震科技星火计划攻关项目(XH17045)
郭松灿(1991年生),男;研究方向流体力学;E-mail: guosongcan@gmail.com
朱庆勇(1969年生),男;研究方向:流体力学;E-mail: mcszqy@mail.sysu.edu.cn
——浙江舟山港主通道百年品质工程建设的理念与措施

