叶片故障时风力发电机组瞬态受力特性分析*

文 | 何建武，刘超，张正川，张洪磊，汪冬冬

叶片故障时风力发电机组瞬态受力特性分析*

文 | 何建武，刘超，张正川，张洪磊，汪冬冬

由于风力发电机组风轮复杂的三维非定常运动，叶片旋转产生时变载荷，从而对结构产生时变激励，这对风力发电机组结构强度有重要影响，而且在某些故障情况下叶片载荷随时间的波动可能会更加剧烈，甚至引起整个结构的破坏，所以有必要对风力发电机组叶片瞬态受力特性及瞬态结构强度进行研究。

在距叶尖三分之一叶长的地方发生断裂是小型离网型风力发电机组常见的叶片断裂情况之一，特别是在内蒙古地区，由于各种原因，故障发生后机组常有带故障运行的情况发生，严重时甚至会造成机组的整体结构破坏，但是未到检修期，故障问题一般难以及时发现并处理。为降低这种常见的叶片断裂故障造成的风力发电机组损坏程度、减小经济损失，有必要在风力发电机组设计初期确定出带故障运行时的结构易受损区域，以进行合理加固。本文针对额定风速下叶片完好、距叶尖三分之一处断裂两种情况，基于单向流固耦合方法，将流场瞬态数值模拟得到的载荷数据进行传递，对风力发电机组结构进行瞬态动力学及结构强度分析，确定出叶片断裂情况下的大应力应变区，为结构的合理优化、故障诊断分析提供一定的参考。

三维模型

本文以国产HY-1000/48小型水平轴风力发电机组为研究对象，其基本参数为：额定转速750rpm，额定功率1000W，启动风速2.5m/s、切入风速3.0m/s、额定风速12m/s、最大承受风速50m/s，风轮直径1.75m，叶片数量5片，整机重量28kg。针对叶片完好、某一叶片距叶尖三分之一处断裂两种情况，利用SolidWorks软件分别建立三维模型，并以轮毂与叶片连接处的轴心（风轮中心）作为原点建立计算坐标系，采用施加合力的方式对轴施加载荷，所以在固体结构计算中省去叶片。简化后的流体、固体计算域三维模型如图1所示。

网格划分和边界条件设置

一、网格划分

由于叶片扭曲，机舱和塔架形状不规则，为保证数值模拟的准确性，需要对固壁边界层进行加密处理以尽量保证y+要求，网格划分采用非结构网格，叶片边界层采用5层棱柱网格，其余流场采用四面体网格。为验证网格无关性，对完好叶片风力发电机组设计五套网格，进行稳态（steady）计算，统计各套网格下风轮输出功率，如表1所示，比较发现，网格四和网格五相差不到2%，则网格满足无关性要求。为节约计算资源，取网格四为计算网格，最终划分结果如图2所示。完好叶片和断裂叶片状态都采用相同的网格划分设置，以保证网格对计算的影响最小。固体采用非结构网格进行划分，最终网格节点数为452589，网格单元总数为211245。划分结果如图2所示。

图1 风力发电机组三维模型

二、边界条件及相关设置

采用CFX软件进行流场数值计算，为保证计算结果的收敛性，以稳态计算结果作为瞬态计算的初始条件。分别对叶片完好、叶片断裂情况下的流场进行数值计算。

稳态计算：进口给定速度值为12m/s，湍流强度10%；旋转域转轴为Z轴，旋转速度750rpm；出口设定为自由出流，给定静压值为一个标准大气压；将地面设置为无滑移壁面，其余面设为对称面；湍流模型选择k-ω SST模型；转动和非转动交界面采用冻结转子模型（Frozen Rotor）；时间步长设为0.0016s；设定收敛残差小于1e-4；最大收敛步长设为5000。

表1 网格无关性验证

图2 网格划分结果

瞬态计算：进出口条件、壁面设置等与稳态计算相同；转动和非转动交界面采用瞬态动静干涉模型（Transient Rotor Stator）；瞬态计算时间总长为1.6s（20圈），时间步长设为0.0016s，每个迭代步最少计算3次，最多计算10次；收敛残差小于1e-4。

采用ANSYS软件瞬态结构计算模块进行风力发电机组结构受力计算。风力发电机组塔架、尾翼材料为45#钢，发电机轴为40铬，机舱外壳材料为铝合金。对于风力发电机组，除受风载荷外，还受到自身重力和底座的固定支撑作用。计算总时间取0.8s（10圈），载荷时间步长设置为0.0016s，从流场中提取两种状态下0.8s到1.6s的面载荷分别施加于固体对应面上。

计算结果分析

一、流场计算结果分析

空气流经叶轮旋转区域时，由于空气和叶片的相互作用，叶片获得来自空气的能量，同时叶片作为阻碍体，对流场有严重干扰，因此，要比较叶片断裂对流场的影响，必须从叶轮旋转区域入手。以图3作为初始状态，过叶轮旋转中心分别作垂直于Y、Z轴的截面Y＝0、Z＝0，将其作为流场分析截面，如图4所示，并选取两种情况下风轮旋转一圈5个典型位置（叶片每旋转72°）的流场进行比较，以分析不同叶片旋转位置下的流场特性。

（一）Z＝0截面压力分布

图5是Z＝0截面不同时刻的静压力分布，该截面通过叶轮旋转中心并穿过叶片，从静压力云图可以看到，叶片表面附近压力较低，且叶尖附近有压力极小值。而叶片断裂情况下，由于断裂叶片缺少叶尖部分，所以没有明显的压力极小值出现。

（二）Y＝0截面速度分布

Y＝0截面平行于塔架并经过叶轮旋转中心，所以该截面的速度分布可以反映经过叶轮后流场的受扰动情况。图6是Y＝0截面不同时刻的速度分布，可以看到两种情况下截面速度分布整体上是一致的。分别截取两种叶片状态下不同时刻的叶片速度矢量，如图7所示，可以看到叶片完好情况下叶尖附近有速度极大值，叶片断裂情况下断裂的叶尖部分速度值明显减小。

（三）叶片受力情况

图3 初始时刻两种风轮状态

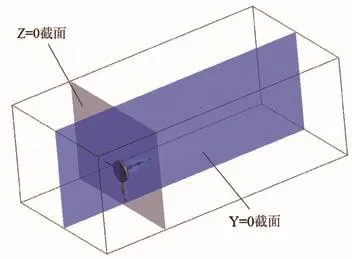
图4 流场分析截面示意图

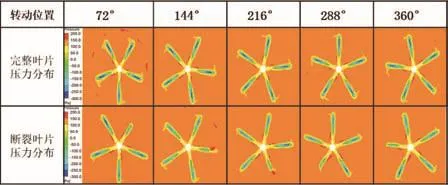
图5 Z=0截面静压力云图

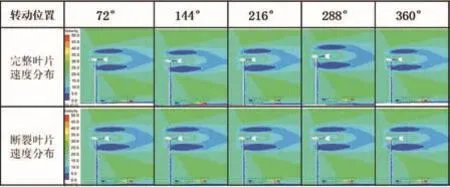
图6 Y=0截面速度分布

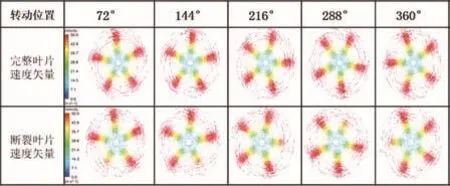
图7 两种情况下叶片速度矢量

为分析叶片在流场中的受力情况，在CFX求解器中设置监控点，以全面监测所有叶片在X、Y、Z方向上合力和合力矩的变化情况。图8给出了0.5s（6.25圈）内两种情况下所有叶片X、Y、Z三个方向所受合力情况。可以看到，在叶片完好情况下，X、Y方向受力在-1N到1N间波动，Z方向受力大小在280N附近波动，波幅较小。叶片断裂情况下，X、Y方向受力在-3N到3N间波动，Z方向受力大小在250N附近波动，波幅较叶片完好情况下的大。图9是0.5s内两种情况所有叶片X、Y、Z三个方向所受力矩情况。叶片完好情况下，X、Y方向力矩在-5N·m到5N·m之间波动，Z轴力矩值在12N·m附近波动。叶片断裂情况下，X、Y方向力矩值在-25N·m到25N·m之间波动，Z轴力矩值在13.5N·m附近波动。

出现这种现象的主要是X轴、Y轴、Z轴的合力矩分别由YZ方向、XZ方向、XY方向合力决定，叶片断裂时叶轮沿Z向的受力面积减小，而周向受力偏离轴心，最终造成Z向受力减小，X方向、Y方向合力波动幅度增大，对应的X轴、Y轴、Z轴力矩波动幅度也随之增大。

二、瞬态结构计算结果分析

采用工程中常用的第四强度理论，即Von Mises屈服条件进行强度分析。由图8、图9可以看到叶片受力具有明显的周期性，为寻找瞬时最大应力出现部位，只需分析旋转一圈内的受力情况则可，因此，对旋转一圈内的几个典型时刻，如1.51s、1.53s、1.55s、1.57s时刻的结构应力分布进行分析。图10是叶片完好情况下不同时刻等效结构应力云图，如图所示，最大应力出现在塔架底部，轴上也有较大应力分布，其余部位应力较小。图11是叶片断裂情况下不同时刻等效结构应力云图，可以看到，最大应力也出现在塔架底部，应力值大小较叶片完好情况明显增大，并且轴、尾舵等部位应力也有增大。

从图10、11可看出，一段时间内，在轴或塔架底部出现应力集中，为研究应力集中部位随时间的应力应变情况，在轴和塔架底部表面各取一监测点，如图12所示，由于旋转的周期性，只需对叶轮旋转一圈的时间内（取1.5s到1.58s）随时间变化的等效应力应变进行提取则可，如图13、14所示。从图中可以看出叶片完好情况下，一个旋转周期内，塔架底部监测点的应力应变随时间的波动程度大于轴监测点，但差距不大；叶片断裂情况下，一个旋转周期内，塔架底部监测点和轴监测点的应力应变随时间的波动程度都被放大，其中塔架底部监测点的波动程度明显大于轴监测点，最大应力增幅达45Mpa；塔架底部监测点和轴监测点的最小应力值差距较小，为12Mpa左右，但最大应力值差距较大，达到了30Mpa左右。因此，对于出现大应力应变的塔架底部区域，应对塔架底部采取一定的优化、加固措施，以保证整体结构强度，并在运行过程中加强对该区域的故障监测。

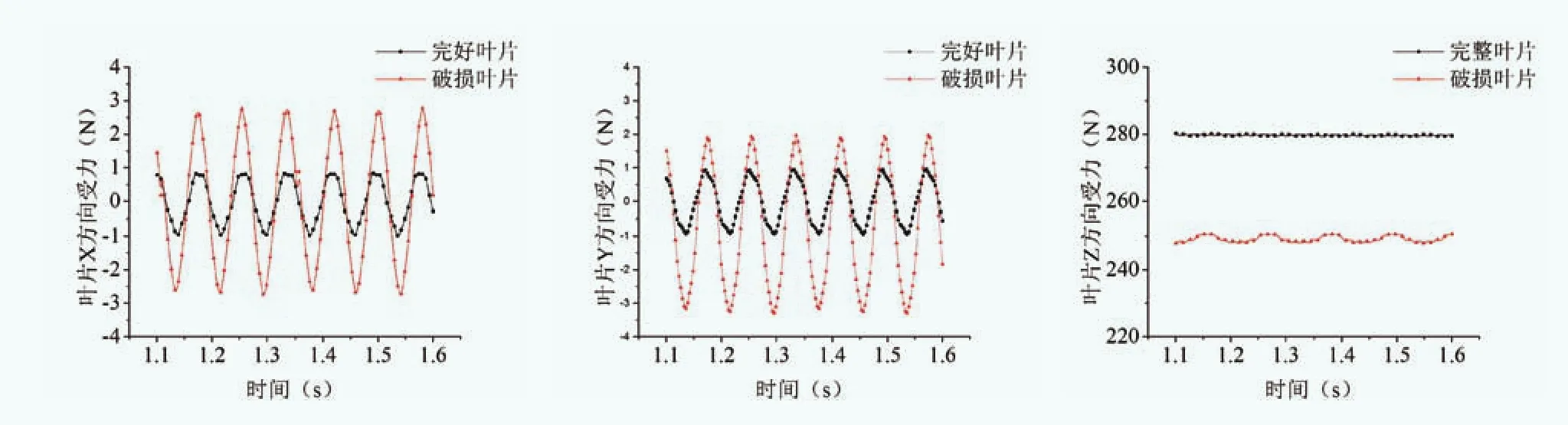
图8 叶片0.5s内受力变化情况

图9 叶片0.5s内力矩变化情况

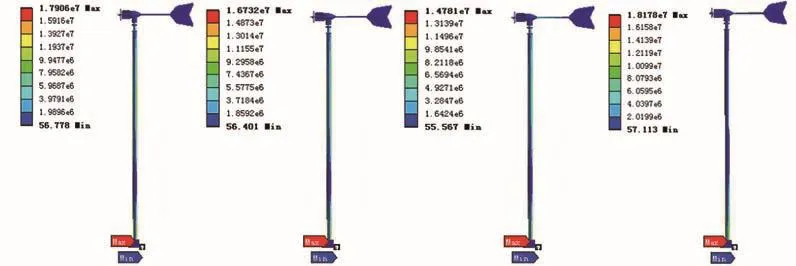
图10 叶片完好情况应力分布云图（1.51s、1.53s、1.55s、1.57s）

图11 叶片断裂情况下应力分布云图（1.51s、1.53s、1.55s、1.57s）

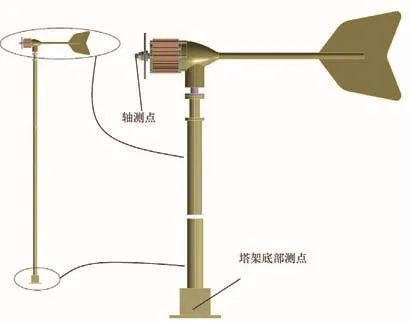
图12 监测点示意图

图13 监测点0.08s内应力

图14 监测点0.08s内应变

结论

本文以某小型水平轴风力发电机组为对象，建立叶片完好和距叶尖三分之一处断裂两种情况的风力发电机组流体、固体计算域三维模型，分别进行流场数值计算，并基于单向流固耦合，分别将提取流场数值计算得到的瞬态载荷，施加于固体结构，进行两种情况下的瞬态结构计算，得到以下结论：

（1）叶片叶尖处断裂会对流场产生扰动，相较于完好叶片，断裂的叶尖压力值有所增大，速度值明显减小，风轮水平和竖直方向的力和力矩随时间波动幅度增大，轴向力有所减小，轴向力矩稍有增大。

（2）利用第四强度理论进行强度分析，结果发现，一个旋转周期内，叶片断裂情况下：塔架底部和轴的最大应力应变值不同程度地增大；塔架底部和轴的应力应变随时间的波动程度都被放大，塔架底部的波动程度明显大于轴；虽然塔架底部和轴的最小应力值几乎相等，但塔架底部的最大应力值几乎是轴的两倍。因此，应对塔架底部采取合理优化、加固措施，以保证结构强度。

上海市青浦区产学研合作发展资金项目（青产学研2015-23）

（作者单位：上海市应用数学和力学研究所）