基于动力总成-整车耦合模型的动力悬置系统振动性能研究
林新有,郝耀东,何智成,李 亮
(湖南大学 汽车车身先进设计制造国家重点试验室,长沙 410082)
基于动力总成-整车耦合模型的动力悬置系统振动性能研究
林新有,郝耀东,何智成,李 亮
(湖南大学 汽车车身先进设计制造国家重点试验室,长沙 410082)
传统的悬置系统分析建立在刚性基础的假设之上,忽略了动力总成与车身、轮胎的耦合作用。建立了包括车身及车轮在内的13自由度动力总成-整车耦合模型,通过模态试验验证了模型的准确性。针对新的耦合系统模型提出了广义解耦率概念,描述动力总成和车身、车身和车轮之间的能量解耦,同时还提出了用来评价动力悬置系统性能的怠速工况、启停工况、路面激励工况。采用新的模型及评价方法对某MPV车型的动力悬置系统进行分析,并采用NSGA-II多目标遗传算法对悬置刚度进行优化。实车试验结果显示,优化后的车内乘员耳边噪声得到有效改善。
动力总成悬置系统;耦合模型;广义解耦率;悬置系统评价;噪声、振动与声振粗糙度
引用格式:
动力总成系统悬置设计是车辆噪声、振动与声振粗糙度( Noise、Vibration、Harshness,NVH)性能研究必不可少的一部分。动力总成悬置系统的主要作用是支撑、限位和隔振。从支撑、限位的角度出发,动力总成的振动幅度不能过大,避免影响动力总成的使用寿命,悬置的橡胶刚度越大越好。然而从悬置的隔振角度出发,需要尽可能衰减发动机传递到车体上的振动,提高整车舒适性,因此悬置的橡胶刚度越小越好,所以两者是一个矛盾体,在悬置设计优化过程中需二者兼顾。目前,在一般动力总成悬置系统的设计优化过程中,主要考虑的设计原则是系统的6自由度解耦或部分解耦,合理匹配悬置系统的固有频率;悬置系统的振动传递率或者支承处的反力最小。
针对动力总成系统悬置的设计,国内外学者进行了大量的研究工作。1979年,美国通用汽车公司的 JOHNSON等在悬置系统的设计中首次应用了数学上的优化技术,以悬置系统的固有频率和模态解耦率为目标函数,以悬置系统的刚度和安装位置为设计变量进行优化设计,大大减小了各个自由度之间的振动耦合度,并且固有频率值在期望的范围内[1-2]。2001年,樊兴华等[3]以整车人机系统为背景,提出了以人体垂向振动加速度均方根的加权值最小和发动机悬置系统能量解耦为综合目标函数的优化模型。2006年,史文库等[4]开发了用于动力总成悬置系统性能分析和优化设计的软件SMMOUNT,并利用该软件进行优化设计,使悬置系统的隔振性能得到改善。
人体振动感觉的频率范围集中在0~30 Hz,在此频率范围内,悬架、悬架和车轮的刚度都起作用,忽略了动力总成与车身、轮胎的耦合作用。传统的动力悬置系统低频振动分析均采用6自由度动力学模型,将悬置直接连接在刚性地面上,没有考虑悬架及轮胎刚度对动力总成模态的影响。实际上,由于悬架及车轮垂向刚度较低,它们对动力总成悬置系统振动尤其是z方向振动的影响不可忽略。
本研究建立了包括车体及簧下质量在内的动力总成-整车耦合系统模型,更为准确地描述了动力总成系统的低频振动,通过怠速工况、启停工况和路面激励工况来描述动力总成悬置系统在不同工况下的振动性能。同时引入了广义解耦率概念,将解耦率由单刚体系统推广至多刚体系统,不仅考虑了传统的6自由度模型的单个系统的能量解耦,还考虑了动力总成和车身、车身和车轮之间的能量解耦。
1 动力总成-整车耦合模型建立
考虑动力总成和车体、车轮之间的耦合关系,建立动力总成-整车耦合模型。新建立的动力总成-整车耦合模型共包括13个自由度,考虑了动力总成所有6个自由度,车体的z向、rx向和ry向3个自由度以及4个车轮的z向自由度。
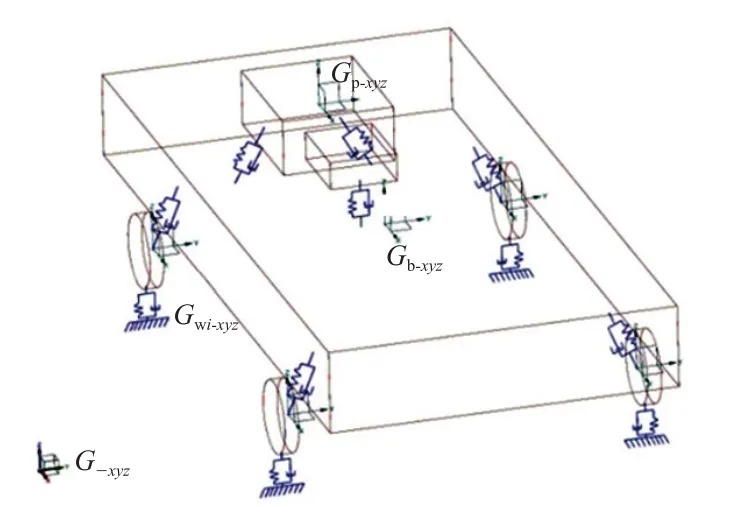
图1 13自由度悬置系统刚体模型
纵置发动机的动力总成-整车13自由度悬置系统刚体模型如图1所示。其中,G-xyz为整车坐标系,原点o为整车质心,x轴与汽车前进方向相反,y轴指向汽车前进方向右侧,z向根据右手法则确定,指向上方。Gp-xyz为动力总成坐标系,原点o为动力总成质心处,x轴与曲轴方向重合,y轴指向垂直曲轴方向右侧,z轴根据右手法则确定。Gb-xyz为车身坐标系,原点o为车身质心,其方向与整车坐标系一致。Gwi-xyz为第i个车轮的坐标系。动力总成质心、车身质心和第i个车轮的位移分别用Xp、Xb和Xit表示,其中,
其参考坐标系为G-xyz。
本研究中的悬置为橡胶悬置。根据橡胶悬置的特性,将其简化为沿垂直于弹性主轴方向的弹性元件,分别表示为ui,vi和wi。悬置具有刚度和阻尼,橡胶悬置在低频的阻尼滞后角变化不大。橡胶悬置的动特性可以采用复刚度Ka或动刚度Kd、滞后角θ表征。复刚度Ka的定义式为:

式中:k1和 k2分别为存储刚度和损失刚度。动刚度和滞后角的定义为:
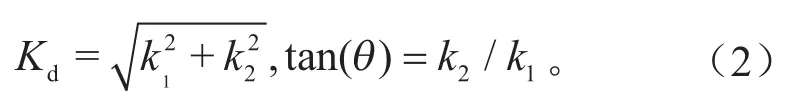
分别建立动力总成、车身及车轮的动力学方程,并将它们耦合为动力总成-车身-簧下质量13自由度系统动力学方程,所有的动力方程均在整车坐标系下建立。悬置的上点为悬置与动力总成的安装中心点,悬置的下点为悬置与车身的安装点。

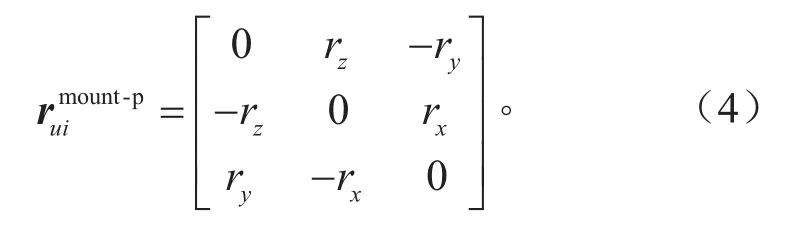
第i个悬置的悬上点在局部坐标中的位移与整车坐标系中的位移之间的关系为:

式中:Ai为第i个悬置的3个弹性主轴在整车坐标系中的方向余弦。
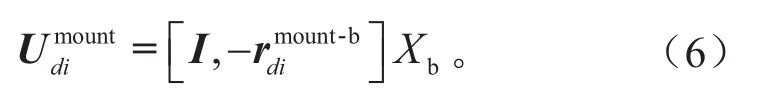

对于第i个悬置,其在局部坐标下力与变形的关系为:
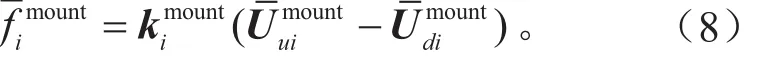
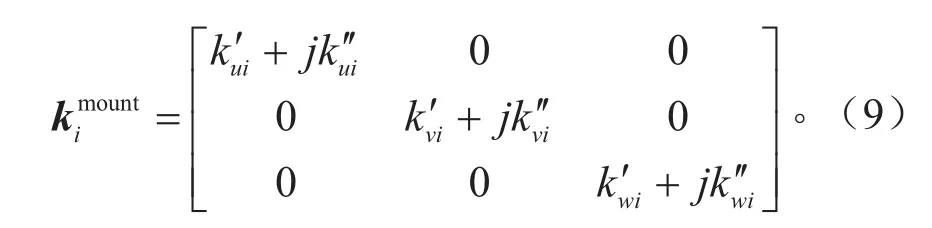
将力fi转换成整车坐标系下的力Fi,有:

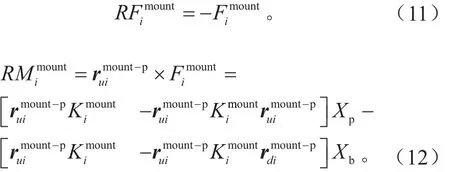
第i个悬置作用于发动机总成上的合力EFMi为:
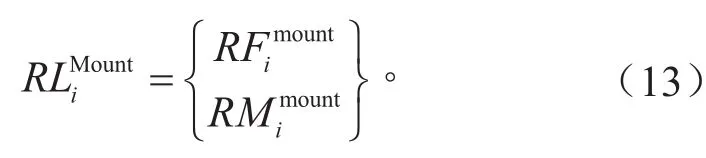
其中,n个悬置点作用于动力总成的合力为:
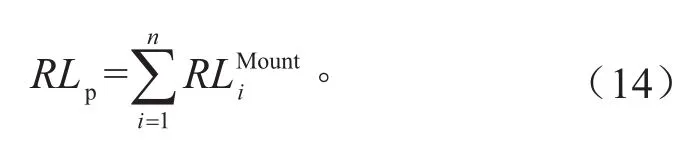
应用牛顿第二定律,动力总成系统的动力方程为 :
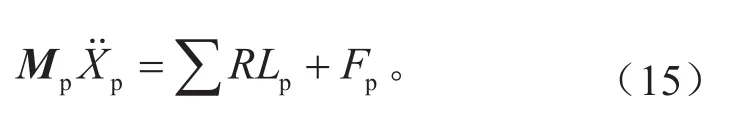
采用上述方法,建立车身系统与4个轮胎系统的动力方程,可得:
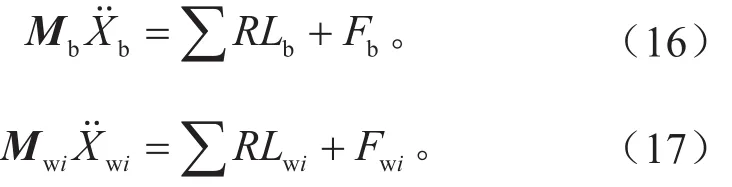
式中:Mp、Mb和 Mwi分别代表动力总成、车身以及4个车轮的质量矩阵;RLP、RLb和RLwi分别代表橡胶悬置、悬架、轮胎对动力总成、车身和4个车轮的合力;Fp、Fb和Fwi则分别表示作用在动力总成、车身和4个车轮上的外力及外力矩。
联立式(15)~(17),得到13自由度系统的动力学方程为:

式(18)中的系统刚度矩阵K可以表示为:


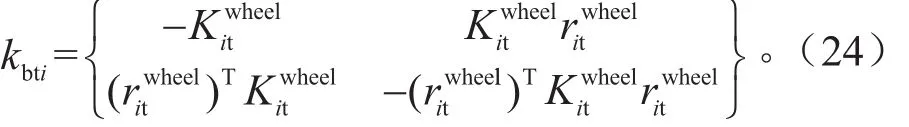
整体质量矩阵M表示为:

由于车身的位移只考虑z向、Rx向及Ry向,轮胎的位移只考虑z向,进行边界条件处理,即可得到动力总成-整车13自由度耦合力学模型。
2 广义解耦率
解耦率为动力总成在某个固有频率下振动时,其能量在各个自由度方向的分布比例。通常,悬置系统的固有频率在多个自由度方向上是耦合的,也就是说,一个方向受到激振就会产生耦合振动,且振动频率带很宽,增加了共振的机会。在本研究所建立的13自由度动力总成-整车系统多刚体模型中,解耦率直接反映发动机与车身之间的耦合程度,可直接计算各子系统之间的振动传递情况,本文定义为广义解耦率。
求解式(18)的特征值,即得到系统的模态,系统在各阶主振动时,其能量全部集中到13个方向,根据系统的质量矩阵和刚度矩阵,可以求出系统在做各阶主振动时各个方向振动能量所占百分比,写成矩阵形式,便得到系统能量分布矩阵。当系统以第j阶固有频率振动时,第k个广义坐标所占的能量百分比Dkj为:
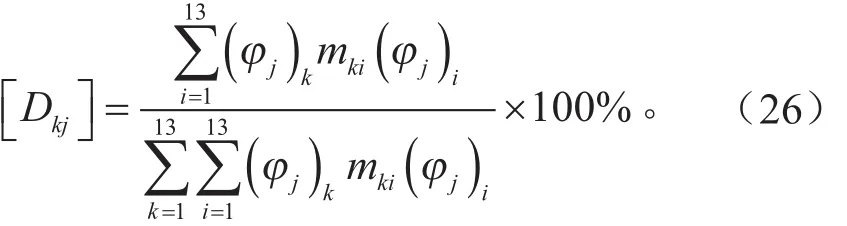
式中:(φj为系统的第j主振型;(φj)k为(φj的第k个元素;mki为质量矩阵第k行、第i列元素。
3 动力悬置系统振动性能分析
当动力总成系统受到外力和外力距F作用时,系统的振动微分方程即为式(18)。
根据上文得到的n个特征值和相应的n个主振型向量A(1), A(2), … A(n)。将各个主振型向量按照固有频率的排列次序按列排成一个矩阵,组成主振型矩阵(主模态矩阵),即
由于主振型向量对质量矩阵和刚度矩阵的正交性,以主振型矩阵作为变换矩阵对式(18)进行坐标变换,即令x= ΦQ,再在式两边左乘以 ΦT得到在模态坐标下的微分方程:
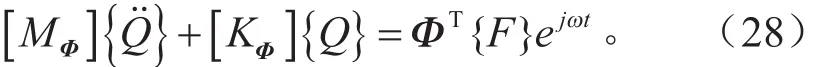
方程完全解耦,如果忽略自由振动,可以求得各个模态坐标的通解为:
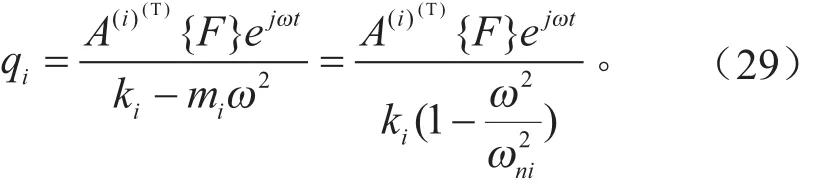
将求得的模态坐标Q下的响应再变换到物理坐标x下,得到系统响应为:
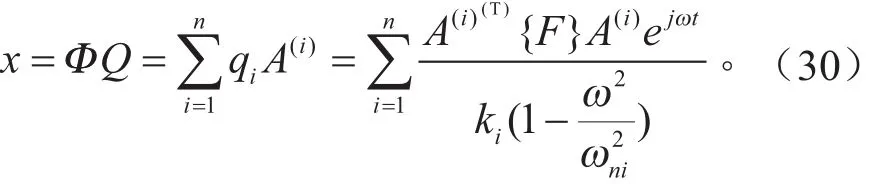
本研究将用以下3个工况下的振动性能的优化情况来评估悬置系统的优化设计,见表1。

表1 悬置振动性能评估方法
3.1 怠速抖动
怠速工况是发动机常用工况,如果悬置系统隔振性能不好,驾驶员会感受到很明显的抖动,对乘坐舒适性有很大影响,所以对悬置系统的隔振性能分析很有必要。仿真中通过在发动机质心处加载沿曲轴转动方向的单位转矩激励,计算动力总成悬置安装点的支反力矩来评判悬置系统的传递率,根据对标车型仿真模型计算结果,要求25 Hz时传递率低于目标值0.12。其计算公式为:

式中:fi为悬置支反力向量:ri为悬置到动力总成质心的位置向量。图2为左悬置振动传递率,由图可知左悬置z向传递率高于目标值。
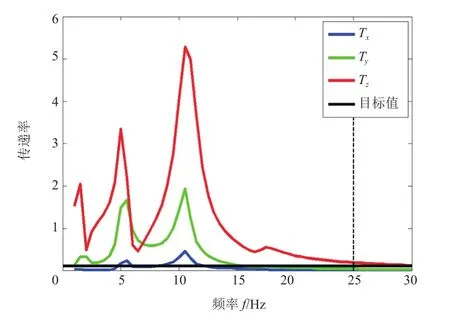
图2 左悬置振动传递率
3.2 启停振动
发动机启停时会产生急剧的力矩变化,所以与之相关的系统会产生噪声与振动,发动机启动可以分成两个阶段,一为电动机拖动阶段,在此阶段所产生的振动主要激励源来自启动反作用力和气缸内的气体压力;二为初始点火阶段,在这此阶段内,主要的激励源则是迅速上升的发动机转矩。
发动机振动控制的途径大致可以分为:削弱激振源、避免共振、减振和隔振。由于削弱激振源和避免共振需要从发动机整体设计上进行规划,在本研究中,主要控制措施为振动隔离,所以对发动机悬置的优化就显得至关重要。启停振动是时域内的瞬态振动,在本研究中把它转换为具有线性悬置刚度的发动机悬置系统频域内的问题,所以对在发动机质心处加载的沿曲轴转动方向的单位转矩的频响分析很容易检验发动机悬置系统的隔振性能。根据对标车型仿真模型计算结果,要求平动加速度峰值低于0.07 m/s²,转动加速度峰值低于1 rad/s²,车身z向加速度低于0.01 m/s²,如图3所示,动力总成绕x向转动加速度和车身z向加速度峰值高于目标值。
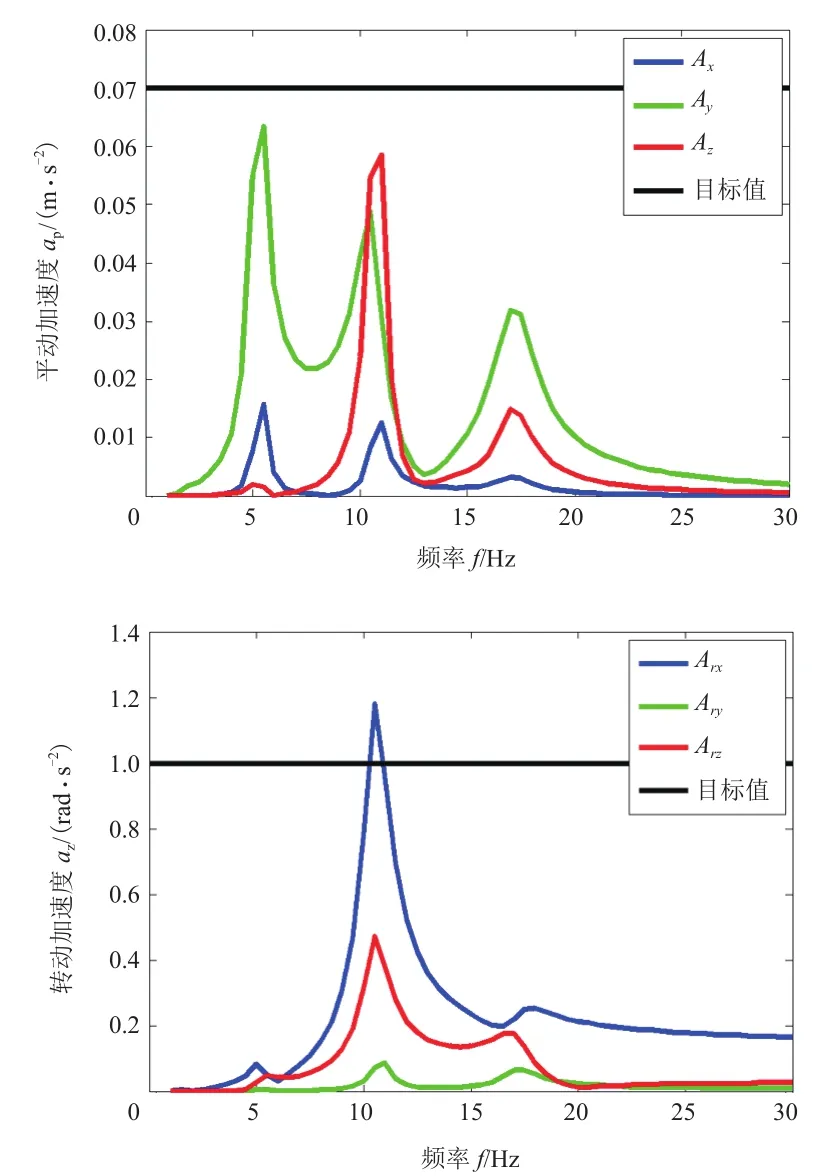
图3 动力总成质心加速度
3.3 路面激励振动
路面激励振动是由路面不平引起的0.5~25 Hz内的低频振动,是汽车振动的基本输入,与动力总成垂直方向的模态和悬置阻尼相关,不同的行车速度和不同的路面情况不一样。解决在随机不平路面激励下整车及零部件的振动问题,是提高汽车行驶平顺性、安全性及零部件可靠性的重要基础。在仿真中,在前轮轮心加载z向单位位移激励,观察动力总成质心和车身追踪点的垂向加速度来评估悬置系统的性能。根据对标车型仿真模型计算结果,要求动力总成z向加速度峰值低于0.01 m/s²,车身z向加速度低于0.005 m/s²,如图4~5所示,动力总成和车身z向加速度均高于目标值。
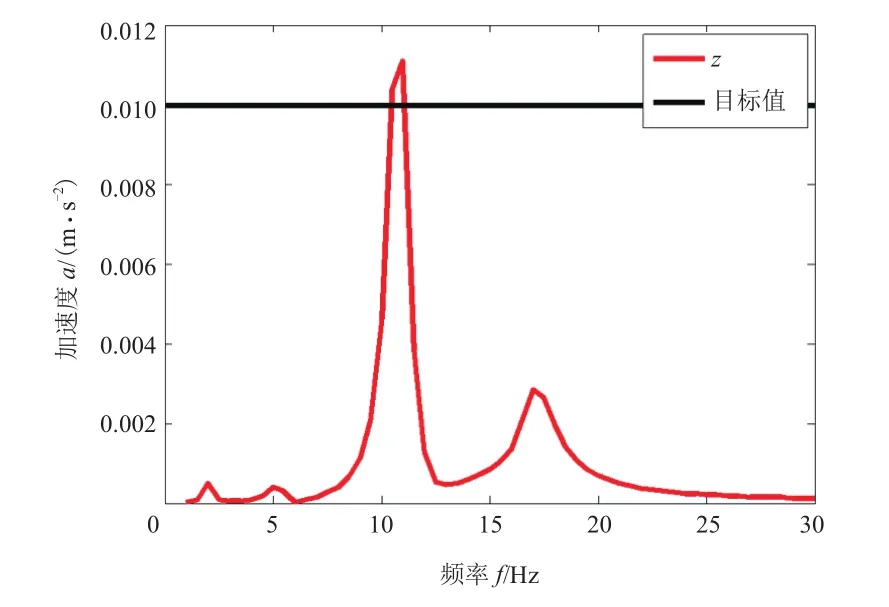
图4 车身z向加速度
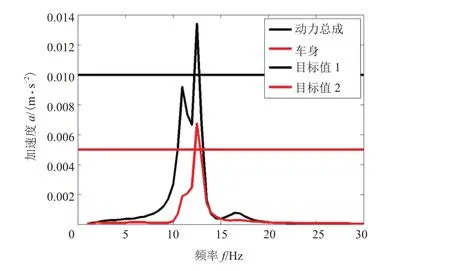
图5 动力总成/车身z向加速度
4 计算实例
某MPV处于开发最后阶段,发动机怠速时振动比较严重,导致车内发动机噪声明显。由于发动机及各部件生产模具已定,不能再更改,现要求对发动机悬置刚度进行优化以达到改善怠速时振动明显的问题,其各项参数见表2~5。

表2 动力总成及车身惯性参数 单位:kg·m2
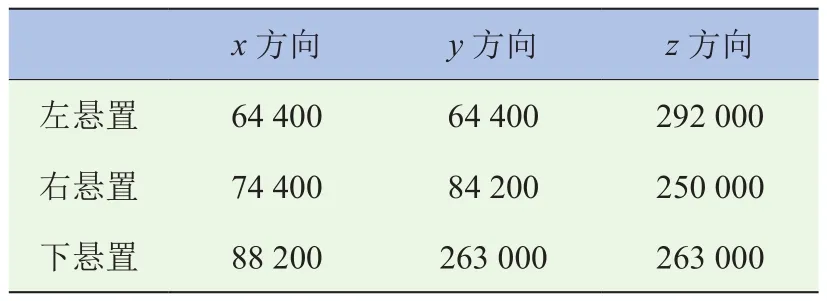
表3 发动机悬置刚度参数 单位:N/m

表4 质量参数 单位:kg

表5 悬架及轮胎刚度参数 单位:N/m
4.1 模型建立和对标
根据上述参数,利用Matlab建立动力总成-整车耦合模型并利用相同的数据建立传统的6自由度系统模型,计算系统模态。由于试验无法测整车的模态,所以此处只测动力总成的模态并与仿真的动力总成模态对比,对比结果见表6。
由表6可知,试验结果与动力总成-整车耦合模型仿真结果前六阶模态更为接近,证明动力总成-整车耦合模型更符合实际情况。

表6 模态对比表 单位:Hz
4.2 固有特性计算
解耦率模态计算结果见表7。

表7 动力总成-整车耦合模型能量分布表
5 优化和验证
能量解耦方法在实际设计中简单方便,应用广泛,能有效地解决耦合振动问题。但该方法存在自身的不足,解耦率指标由悬置的各个方向刚度的比例关系确定,任何一组相同比例的悬置刚度值对应的动力总成系统具有相同的解耦率指标,但具有不同的车内振动情况,而评价车辆NVH性能的好坏更多的是关注车辆驾乘人员的环境-驾驶室的振动噪声情况。因此,本研究利用NSGA-II[12]多目标遗传算法来优化系统解耦率,然后利用提出的新方法评估系统振动性能来确定最终方案。
5.1 悬置性能优化
由于此车型已处于开发最后阶段,发动机与变速器型号已定,现以动力总成悬置系统的9个刚度参数为优化对象,应用遗传优化算法,利用Isight结合Matlab数学模型进行多目标优化,要求各向解耦率最大。得到优化后的刚度参数见表8,优化后的模态和能量分布见表9,可以看出优化后动力总成解耦率有明显提高,其中z向由44.8%提高到71.3%,Ry和Rz向分别由约58%提高到72%,并且车身和动力总成的耦合现象明显下降。
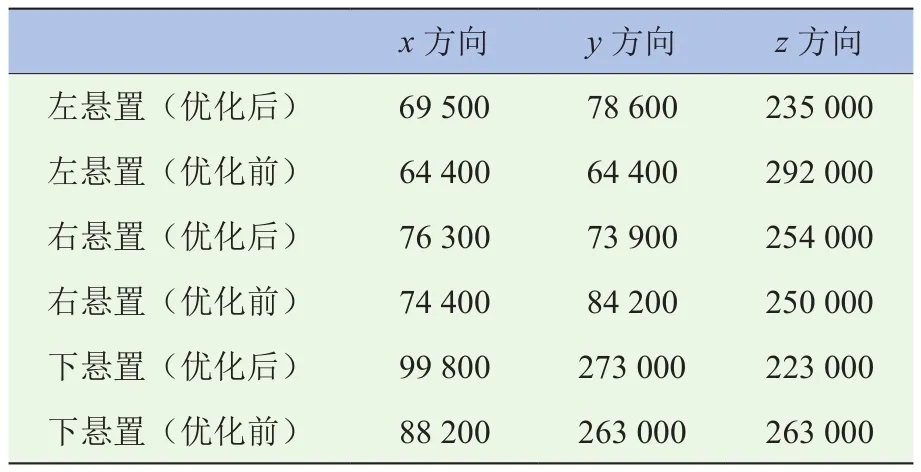
表8 优化前后悬置刚度参数 单位:N/m

表9 优化后动力总成-整车耦合模型能量分布表
5.2 优化结果验证
对优化后的动力总成系统进行振动性能分析,结果如图6~8所示。由图6可知,优化后左悬置z向传递率在25 Hz时低于目标值0.12;由图7可知,优化后动力总成转动加速度和车身z向加速度都低于目标值;由图8可知,优化后动力总成z向加速度低于目标值,但是车身z向加速度变化不大,依然高于目标值。综上所述,认为此优化方案满足要求。
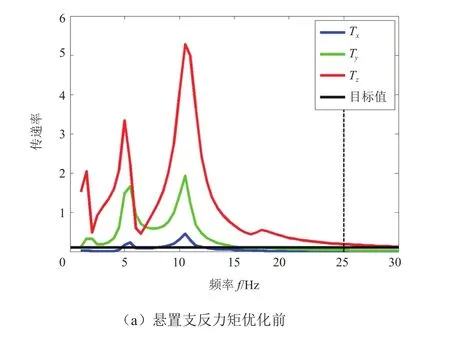
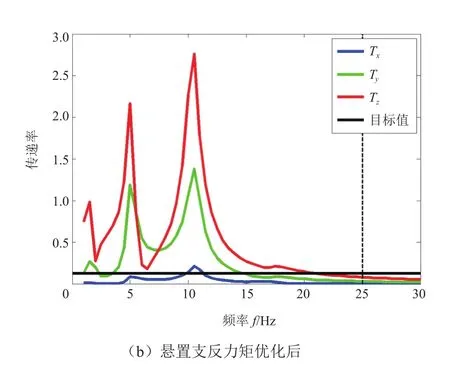
图6 怠速抖动
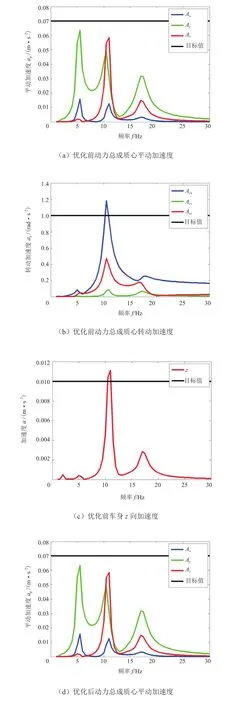

图7 启停振动时车内座椅导轨处z向加速度

图8 路面激励振动
5.3 实车试验
为了验证仿真的可行性,对原样车和替换优化后橡胶悬置的样车分别安装进行噪声试验,对怠速关空调及3挡全油门关空调两种工况进行试验验证。
在怠速关空调工况下,优化前后车内噪声测试频谱分析图如图9所示。由图可知,优化后驾驶员耳边噪声有较大改善,怠速工况驾驶员右耳声压级幅值下降2.6 dB。
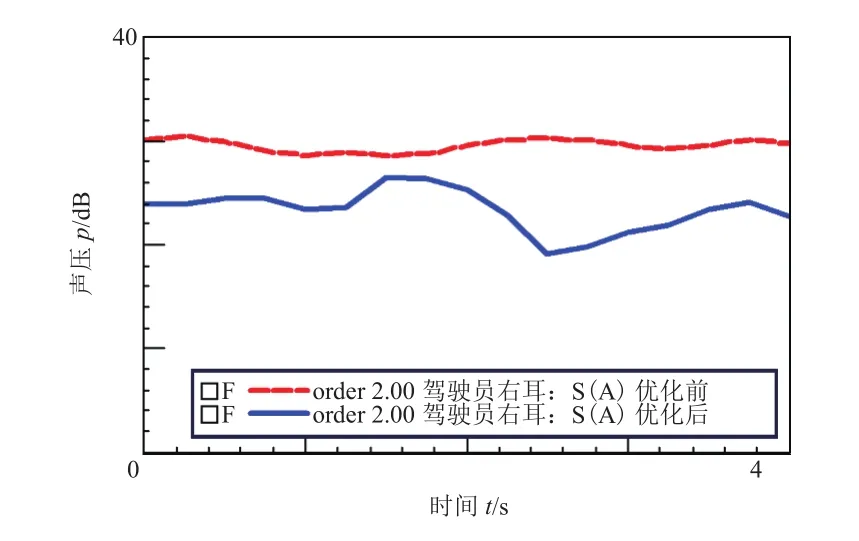
图9 驾驶员耳朵处二阶噪声响应
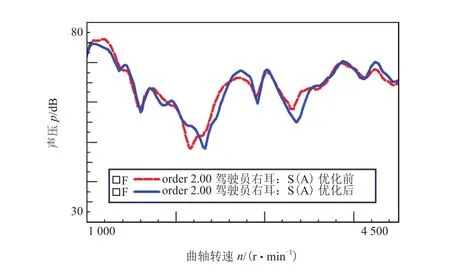
图10 三挡全油门加速度工况驾驶员耳朵处二阶噪声响应
在3挡全油门加速关空调工况下,优化前后车内噪声测试频谱分析图如图10所示。由图可知,优化后驾驶员耳边噪声和后排乘客耳旁噪声都有改善,3挡全油门加速工况驾驶员右耳旁声压级幅值下降1.3 dB。
6 结论
(1)建立动力总成-整车耦合模型,包括动力总成、车体、簧下质量在内的13个自由度。考虑了动力总成与车体之间的耦合作用,并克服了传统6自由度模型刚性基础假设的缺点。
(2)针对建立的动力总成-整车耦合模型,提出广义解耦率的概念,不仅反映了单刚体各个方向的振动能量分布情况,还反映出各子系统之间的能量分配。
(3)提出针对不同工况的动力传动系统振动性能评价方法,包括怠速、启停及路面激励三大工况,阐述了各个工况的作用、激励形式及结果评价。
(4)针对某款MPV车型怠速噪声大的问题,采用本文提出的建模及评价方法对该车型动力悬置系统性能进行分析,并采用NSGA-II算法对悬置刚度进行优化。根据怠速关空调及3挡全油门加速工况下的实车试验结果,发现优化后怠速工况下驾驶员耳旁二阶噪声最大值分别降低2.6 dB和1.3 dB,怠速噪声得到了改善。
参考文献(References):
[1]JOHNSON S R,SUBHEDAR J W. Computer Optimization of Engine Mounting Systems [C]//SAE Technical Papers,790974,1979.
[2]上官文斌. 汽车动力总成悬置系统振动控制设计计算方法研究 [J]. 振动工程学报,2007,20(6):577-583.SHANGGUAN Wenbin. Calculation Methods for the Vibration Control Design of a Powertrain Mounting System[J]. Journal of Vibration Engineering,2007,20(6):577-583.(in Chinese)
[3]樊兴华,陈金玉,黄席樾. 发动机悬置系统多目标优化设计[J]. 重庆大学学报(自然科学版),2001,24(2):41-44.FAN Xinghua,CHEN Jinyu,HUANG Xiyue. Multiobject Optimization Design of Engine Mounting System Parameters [J]. Journal of Chongqing University (Natural Science Edition),2001,24(2):41-44. (in Chinese)
[4]史文库,洪哲浩,赵涛. 汽车动力总成多目标优化设计及软件开发[J]. 吉林大学学报(工学版),2006,36(5):654 -658.SHI Wenku,HONG Zhehao,ZHAO Tao. Automobile Multi-objective Optimization Design of Power Assembly Mounting System and Software Development [J]. Journal of Jilin University (Engineering and Technology Edition),2006,36(5):654 -658.(in Chinese)
[5]吴飞. 综合考虑解耦率和隔振率的发动机悬置系统多目标优化 [J]. 汽车工程,2013,35(1):18-22.WU Fei. The Multi-objective Optimization of Engine Mount System Concurrently Considering Energy Decoupling Rate and Vibration Isolation Rate [J]. Automotive Engineering,2013,35(1):18-22. (in Chinese)
[6]HATA H,TANAKAH. Experimental Method to Derive Optimum Engine Mount System for Idle Shake [C]//SAE Technical Papers,870961,1987.
[7]JEONG T,SINGH R. Analytical Methods of Decoupling the Automotive Engine Torque Roll Axis [J]. Journal of Sound and Vibration,2000,234(1):85-114.
[8]吕兆平. 能量法解耦在动力总成悬置系统优化设计中的应用 [J]. 汽车工程,2008,30(6):523-526.LYU Zhaoping. The Application of Energy Decoupling Technique to Powertrain Mounting System Optimization[J]. Automotive Engineering,2008,30(6):523-526. (in Chinese)
[9]黄鼎友,吉向东. 动力总成悬置系统建模及振动仿真[J].江苏大学学报(自然科学版),2005,26(3):222-226.HUANG Dingyou,JI Xiangdong. Modeling of Engine Mounting System and Its Vibration Simulation [J]. Journal of Jiangsu University (Natural Science Edition),2005,26(3):222-226.(in Chinese)
[10]周冠男,蒋伟康,吴海军. 基于总传递力最小的发动机悬置系统优化设计 [J]. 振动与冲击,2008,27(8):56-58.ZHOU Guannan,JIANG Weikang,WU Haijun. Optimum Design of Engine Suspension System Based on Minimum Total Transmission Force [J]. Journal of Vibration and Shock,2008,27(8):56-58.(in Chinese)
[11]陈剑,徐陈夏.发动机悬置系统优化设计及其可靠性分析 [J]. 汽车工程,2009,31(3):234-238.CHEN Jian,XU Chenxia. Optimization Design and Reliability Analysis of Engine Mount System [J]. Automotive Engineering,2009,31(3):234-238. (in Chinese)
[12]DEB K,PRATAP A,AGARWAL S,et a1. A Fast and Elitist Multi-objective Genetic Algorithm:NSGA-Ⅱ [J].IEEE Transactions Oil Evolutionary Computation,2002,6(2):182-197.
Research on Vibration Performance of Powertrain Mounting System Based on a Model Coupling the Powertrain and Vehicle
LIN Xinyou,HAO Yaodong,HE Zhicheng,LI Liang
(State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha 410082,China)
A traditional powertrain mounting model is constructed based on the rigidity assumption, which ignored the coupling effect between the body and wheels. This paper firstly built a 13 DOF rigid model for the powertrain mounting system including the body and wheels and the effectiveness of this model was further verified through modal tests. Secondly, the concept of generalized decoupling rate was established for this novel coupled system and was used to describe the effect of decoupled energy between the powertrain and body and between the body and wheels. Thirdly, three kinds of driving conditions including idling, key-off/on, and road excitation were applied to assess the performance of the powertrain mounting system. Finally,the proposed method was employed to analyze a MPV's powertrain mounting system, and by optimizing the mount stiffness through the multi-objective genetic algorithm (NSGA-II), the acoustic pressure response of the driver's ear is improved.
powertrain mount system;coupled model;generalized decoupling rate;mount system assessment;NVH
TB535
A
10.3969/j.issn.2095-1469.2017.05.07
2017-03-09 改稿日期:2017-04-10
湖南大学汽车车身先进设计制造国家重点实验室自主研究课题(31175002);重庆理工大学汽车零部件教育部重点实验室2014年开放课题(2014KLMT04);柳州市柳东新区科学技术研究与技术开发计划项目(柳东科攻20130301)
林新有,郝耀东,何智成,等. 基于动力总成-整车耦合模型的动力悬置系统振动性能研究 [J]. 汽车工程学报,2017,7(5):357-367.
LIN Xinyou,HAO Yaodong,HE Zhicheng,et al. Research on Vibration Performance of Powertrain Mounting System Based on a Model Coupling the Powertrain and Vehicle [J]. Chinese Journal of Automotive Engineering,2017,7(5):357-367. (in Chinese)
作者介绍

责任作者:林新有(1991-),男,江西赣州人。硕士研究生,主要研究方向为整车振动噪声控制。
Tel:15307829770
E-mail:xylin2014_hnu@126.com

郝耀东(1988-),男,河北邯郸人。博士研究生,主要研究方向为整车NVH性能开发及底盘NVH、数值计算方法。
Tel:18607724120
E-mail:hao_yaodong@foxmail.com

