直管流致振动数值模拟中的参数选择

杨 凡，鲁 丽

(西南交通大学 a.力学与工程学院; b.应用力学与结构安全四川省重点实验室， 成都 610031)

直管流致振动数值模拟中的参数选择

杨 凡a，鲁 丽b

(西南交通大学 a.力学与工程学院; b.应用力学与结构安全四川省重点实验室， 成都 610031)

基于ANSYS Workbench与CFX有限元分析软件，采用双向流固耦合方法，以横向流作用下的单根直管为基本分析对象，建立三维流固耦合模型。利用Meshing划分不同网格来研究网格划分对单管的流致振动数值模拟的影响。以横向均匀来流下单管为例，给出了合理的边界层网格划分方式及合理的时间步长。

流致振动；双向流固耦合；数值模拟；Workbench

在生产与生活中管束振动问题不可忽视。实际应用中发生流致振动的部件大多可以简化为圆柱结构，流体对圆柱结构的冲刷会引起部件的损伤，从而对结构总体安全带来严重的危害[1]。流体引发的振动从运动方向上可以分为纵向流和横向流，纵向流沿轴线方向，横向流垂直于轴线方向，即使在流速不大时，横向流也会引发管的振动。不同流速下引发振动的机理主要有涡激振动、湍流抖振、流体弹性不稳定性和声共振4种[1]。

目前，对管束结构的流致振动各项机理进行了大量研究，其方法之一为通过实验数据确定流体力系数，但由于所需参数过多，因此有一定的局限性。随着数值方法和计算机技术的不断发展，已经可以采用有限元软件对其进行数值模拟的方法。王亚玲等[2]发现高雷诺数时圆柱周围的流动具有明显的三维特性。M.Breuer[3]采用大涡模拟方法对高雷诺数下孤立圆柱绕流问题进行了三维数值模拟，结果表明：采用大涡模拟方法进行圆柱绕流的三维数值计算和实验结果吻合得较好。一个完整的流固耦合分析包含3个过程：单独的结构分析、单独的流体场分析、耦合边界数据传递，其重点在于流体网格划分及流固耦合面设置。

1 模型建立

经典的流固耦合系统分为强耦合和弱耦合两大类，整体趋向于利用N-S方程与非线性结构动力学求解。流固耦合问题一般分为两类：流-固单向耦合和流-固双向耦合。单向耦合适用于流体对固体作用后固体变形不大的情况，即流体的边界形貌改变很小，不影响流体分布。与单向流固耦合不同，流体的结果在输出给结构以后，固体结构的计算结果也反向对流体产生作用，当固体结构变形比较大、导致流体的边界形貌发生改变后，流体分布会有明显变化[4]。因此，本文使用双向流固耦合方法，打开大变形选项，流体与固体使用相同的耦合时间步，设定动网格，设置结构与流体接触面为流固耦合面。

本文选取的模型参数如下：管长L=0.5 m，外径D=0.01 m，内径d=0.095 m，弹性模量E=10 GPa，泊松比ν=0.3，管子的密度为6 500 kg/m3，阻尼比ξ=0.047。流体模型为水，流场入口流速为2 m/s。湍流强度为

(1)

本文选用雷诺数为104量级，得到I=5%，故选用中等湍流强度。

流场大小对数值模拟结果有很大影响，为了简化计算并且使结果尽可能准确，根据文献[5-6]，当轴线选择距离出口15D以上时，压强接近于0，宽度大于8D时，碰壁现象消失，高度大于πD时足以正确描述漩涡特性。基于此，本文最终选择流场尺寸为20D×10D×50D。

建立的物理模型如图1所示，其中：入口采用速度入口边界条件，出口为压力出口，管外壁为FSI；同时设置为动网格边界。在圆管中间截面处设置监测点1～4，如图2所示。

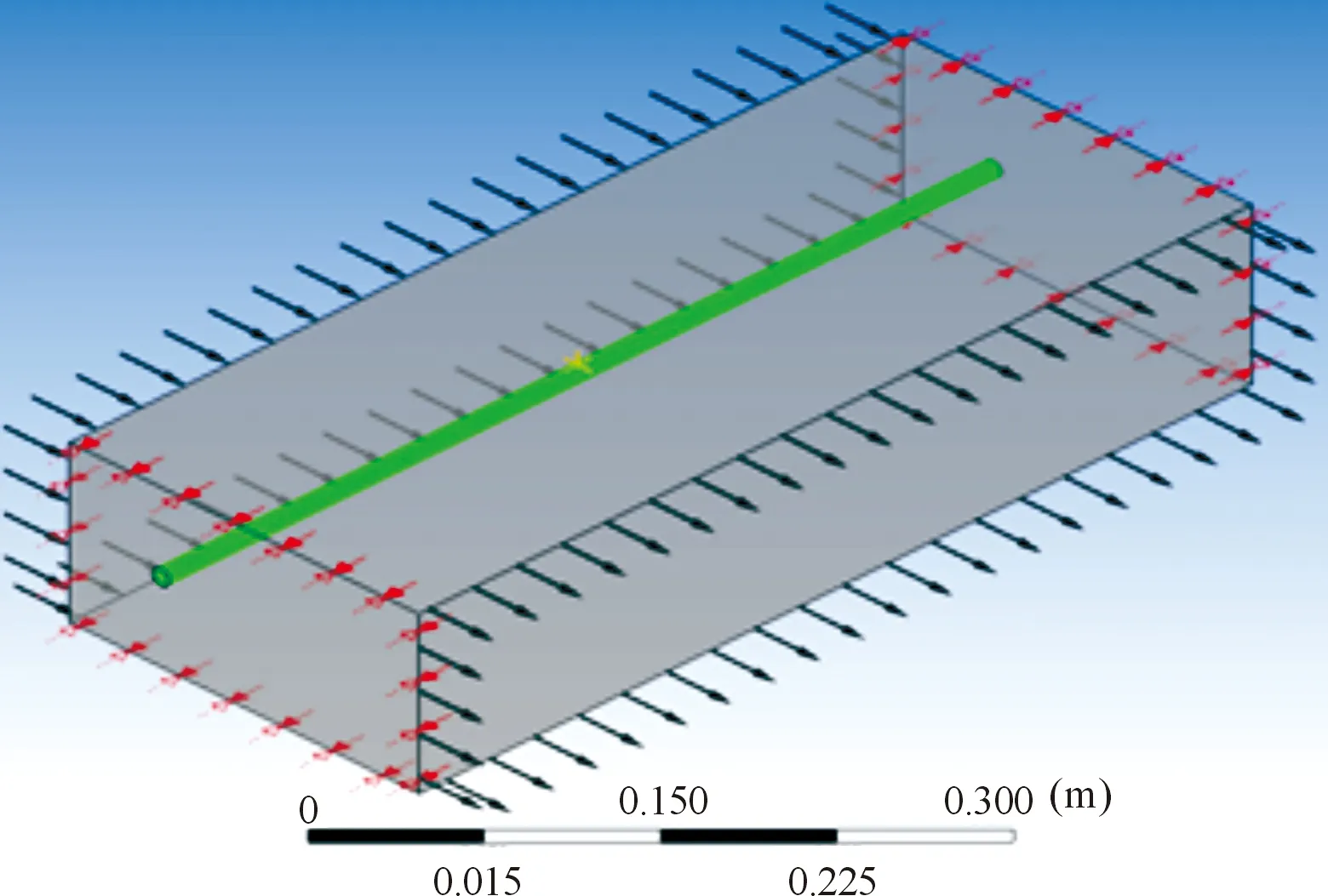
图1 物理模型

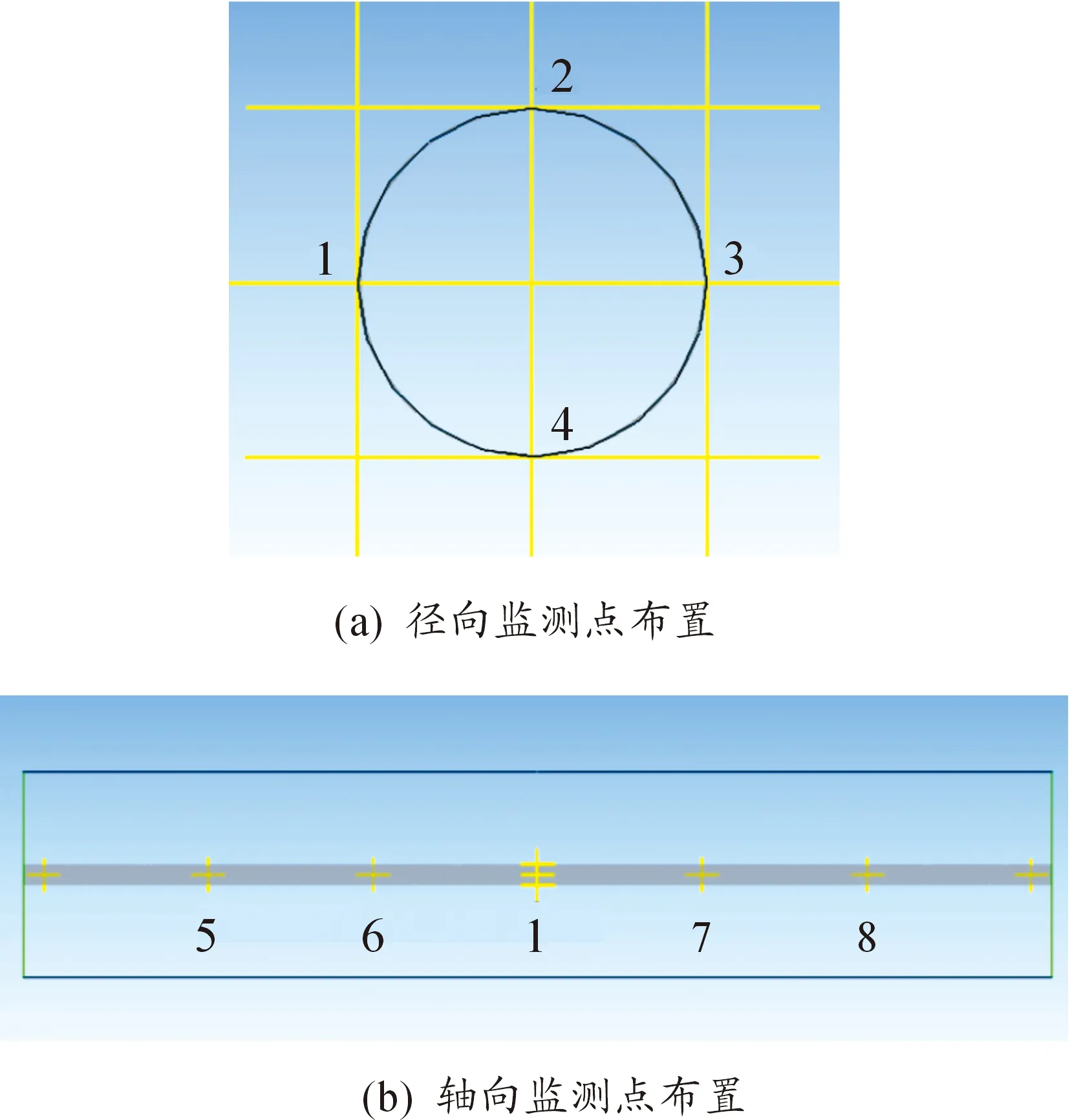
图2 监测点布置

2 网格及时间步长选取

2.1 网格对数值计算的影响

采用三维建模软件SolidWorks分别建立流体与结构模型，将之导入Workbench中的Geometry进行模型编辑，并划分网格。得到的网格质量虽然很好，但由于未划分边界层网格，监测点处位移不准确，数值模拟结果不可信，如图3所示。因此，为了得到理想的结果，在划分网格时必须细化网格，并在流固耦合面周围划分边界层网格。

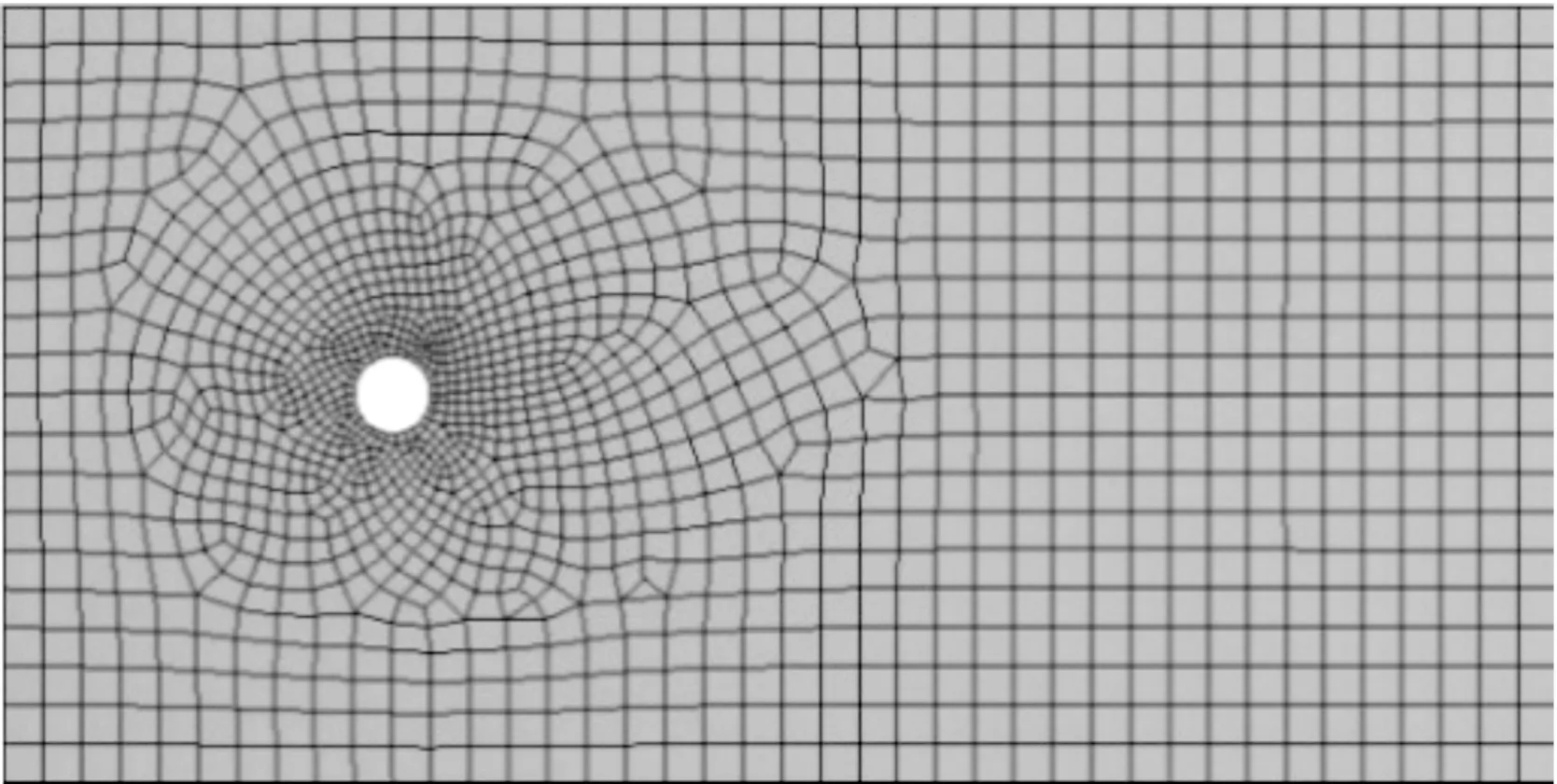
图3 未划分边界层

根据边界层网格选取标准，边界层第1层网格比较关键，厚度大概是基本尺寸的25%。边界层不应增长太快，一般增长因子选择在1.3以下，否则会影响到差分精度。为了保证边界层过渡稳定，一般取边界层网格层数为5～10层。本文选择边界层厚度为0.05 mm，增长因子为1.1，共10层。重新划分后结构网格数为6万，流体网格数为315万。

在运算过程中，因结构网格数目过大，运算对计算资源要求较高，故需要对结构重新划分网格，在控制结构网格数量的同时保证边界层网格密度。如图4所示，重新划分后边界层网格质量较好，流体网格数从315万减少至120万，固体结构部分网格数为9 000，计算量大大减小。

对计算结果进行处理。图5为管表面监测点处位移时程曲线。在划分较好的边界层网格以后，可以得到较准确的结果。同时可知，监测点处在受到流体冲击时，当流速较小先产生振动，随后逐渐趋于稳态。由此可知：在ANSYS Workbench中，通过对流体边界层网格进行细分，可以快速高效地进行数值模拟并保证结果可靠。

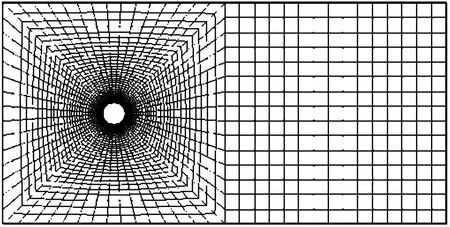
图4 最终网格分布

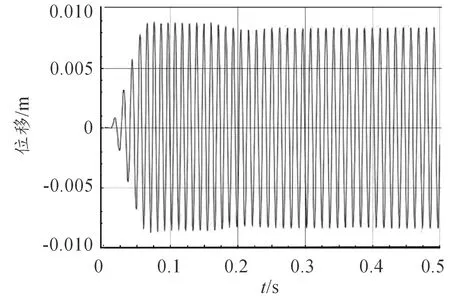
图5 监测点处位移时程曲线

2.2 时间步长选取

CFX使用耦合求解器，因此在流固耦合计算中流场的收敛问题十分关键，是导致整个计算是否收敛的一大因素，除了通过提高网格质量和有限元单元密度来提高收敛度以外，也需要设置较小的时间步长来提高收敛度。在用CFX求解时，如果选择的时间步长很大，则需要的迭代次数较少，但也可能引起求解器不稳定甚至发散；如果选择的时间步长很小，收敛会很稳定，但是需要很多的迭代，速度较慢。因此，合适的时间步长选择对于收敛非常重要[7-8]。

本文分别选取时间步长为0.000 25 s及0.000 50 s两种情况，总计算时长为0.5 s。基于ANSYS Workbench与CFX有限元分析软件，设置残差收敛精度，采用耦合求解器并行运算。

当最后一次交错迭代的6个值小于0时，即可满足该时间步长的收敛。如图6所示，当时间步长为0.000 25 s时，收敛情况较好，但速度较慢。选用时间步长为0.000 50 s，数值模拟结果收敛较好，且计算速度较快。因此，综合考虑计算周期及计算的精度，本文取计算的时间步长为0.000 50 s。

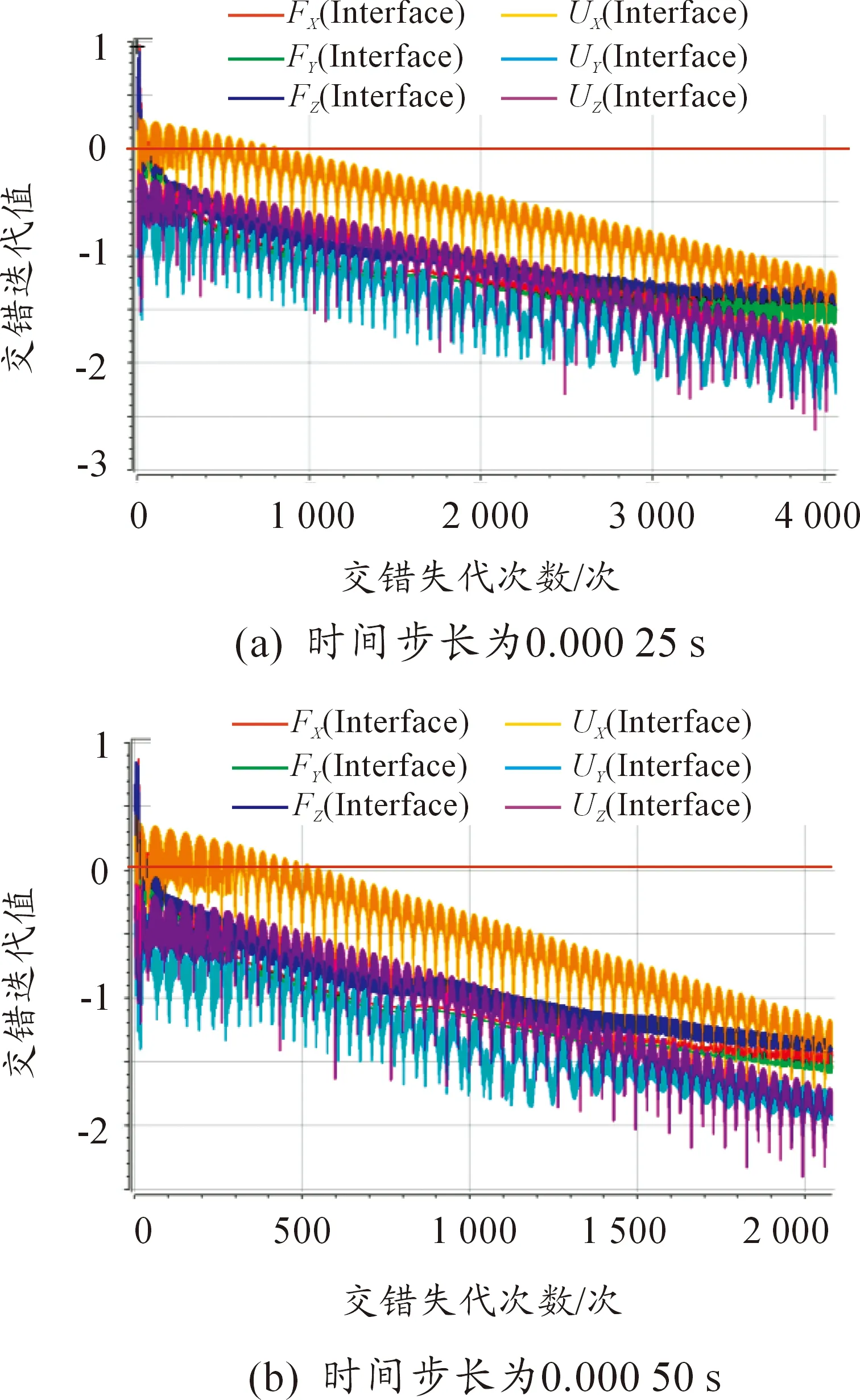
图6 交错循环迭代过程

3 结束语

本文使用有限元分析软件，采用双向流固耦合的方法，对横向流作用下的单根直管进行网格划分并求解。结果发现：网格的不同划分方式对单管流致振动的数值模拟有较大影响。

在工程上，当流固耦合系统尺寸较大时可通过缩比模型降低计算量。同时，在不影响收敛精度的基础上，选用合适的时间步长也可以有效提高数值模拟效率。

[1] WEAVER D S，ZIADA S，AU-YANG M K,et al.Flow-induced vibrations in power and process plant components—progress and prospects[J].Journal of Pressure Vessel Technology,2000,122(3):339-348.

[2] 王亚玲,刘应中,缪国平.圆柱绕流的三维数值模拟[J].上海交通大学学报,2001,35(19):1464-1469.

[3] BREUERM.A challenging test case for large eddy simulation high Reynolds number circular cylinder flow[J].Heat and Fluid Flow,2000(21):648-654.

[4] 宋学官.ANSYS流固耦合分析及工程实例[M].北京：中国水利水电出版社,2012.

[5] PONTAZA J P,CHEN H C.Three-dimensional numerical simulations of circular cylinders undergoing two degree-of-freedom vortex-induced vibrations[C]//Proceedings of 25th international Conference on Offshore Mechanics and Arctic Engineering.Germany:Hamburg,2006.

[6] DONG S,KARNIADAKIS G E.DNS of flow past a stationary and oscillating cylinder atRe=10 000 [J].Journal of Fluids and Structures,2005(20):519-531.

[7] 邢景棠，周盛，崔尔杰.流固耦合力学概述[J].力学进展,1997,27(1):20-38.

[8] 白冬强，孙欣杰.基于流固双向耦合仿真的热气球装置空气外流场分析[J].重庆理工大学学报(自然科学)，2015(2):61-64.

(责任编辑刘 舸)

ParameterSelectioninNumericalSimulationofFlow-InducedVibrationofStraightPipe

YANG Fana, LU Lib

(a.School of Mechanics and Engineering; b.Key Laboratory of Mechanics and Structural Safety of Sichuan Province,Southwest Jiaotong University, Chengdu 610031, China)

Based on ANSYS Workbench and CFX finite element analysis software, a three-dimensional fluid-solid coupling method was established to analyze the single straight tube under the transverse flow. Workbench Meshing was used to divide different types of grids, and the effect of different gridding on the numerical simulation of flow-induced vibration system was considered. With the two-way fluid-solid coupling method, a reasonable boundary layer gridding meshing and time step were given for a single tube with transverse flow.

flow-induced vibration; two-way coupling; numerical simulation; Workbench

2017-06-28

国家自然科学基金资助项目(11372258,11302183,11302181)

杨凡(1992—),女,陕西人,硕士研究生,主要从事流固耦合动力学研究，E-mail:kikoyang@live.cn。

杨凡，鲁丽.直管流致振动数值模拟中的参数选择[J].重庆理工大学学报(自然科学)，2017(10):62-65.

formatYANG Fan, LU Li.Parameter Selection in Numerical Simulation of Flow-Induced Vibration of Straight Pipe[J].Journal of Chongqing University of Technology(Natural Science)，2017(10):62-65.

10.3969/j.issn.1674-8425(z).2017.10.010

O351.2

A

1674-8425(2017)10-0062-04