纵向数据下半参数Logistic模型的变量选择

高仙立，姜玉英

（1.首都经济贸易大学 统计学院，北京 100070；2.北京印刷学院 基础部，北京 102600）

纵向数据下半参数Logistic模型的变量选择

高仙立1，姜玉英2

（1.首都经济贸易大学 统计学院，北京 100070；2.北京印刷学院 基础部，北京 102600）

文章研究了纵向数据半参数Logistic回归模型的估计问题，给出了模型中未知参数和未知函数的估计方法，探讨了参数部分的变量选择问题，并对不同的变量选择方法进行比较分析。从模拟结果可以看到，文中给出的方法具有很好的估计效果。

纵向数据；半参数Logistic模型；变量选择

0 引言

纵向数据指同一研究对象在不同时点上的观测数据，与计量经济学中广泛应用panel数据不同，纵向数据不要求所有研究对象的观测时点相同，因而在实际应用中更为普遍。对于纵向数据参数回归模型的估计问题，目前已经有了一些研究成果，如Diggle等（2002），Fu和Wang（2016）等。当前，随着实验技术、检验手段的日益提高，所获数据的变量个数越来越多，变量选择显得尤为重要。关于变量选择的研究一直是众多统计学者的研究热点，学者们提出了一系列标志性的变量选择方法，例如：岭回归、桥回归、lasso、SCAD、Adaptive lasso、Adaptive Robust lasso等。但这些研究大都针对响应变量为数量型变量的情形，针对分类数据的情形目前研究甚少。因此，本文将把变量选择问题的研究领域拓展到分类数据中，研究纵向数据下Logistic回归模型的变量选择问题。

半参数Logistic回归模型既保持了非参数模型的灵活性与参数模型的简洁性，又可以对分类数据进行建模。通过采用等间距样条函数逼近非参数部分，将非参数问题转化为参数问题，给出非参数部分的全局拟合值。在此基础上，采用极小化惩罚似然的方法，得到常系数部分和非参数部分的估计。本文的惩罚函数主要使用lasso与SCAD，从不同角度刻画惩罚方法的优劣。

1 模型与估计方法

考虑二分类变量Y和p维协变量X的纵向统计建模问题。假设获得如下纵向数据：

这里Yij和Xij=(Xij1,…,Xijp)T分别为第i个个体在第j个观测时间Tij时的观测值。通常假定mi有界。

记Xi=(Xi1,…,Ximi)T，Ti=(Ti1,…,Timi)T，其中Xij为p维列向量，Ti为mi维列向量，建立纵向数据的半参数Logistic回归模型如下：

其中β=(β1,…,βp)T为p维未知参数向量，g(t)为未知光滑函数。并记：

其中时间变量Tij的取值范围在0到T之间，μ(x)为Logistic函数，即称为联接函数，且满足严格单增。当连接函数退化为恒等映射时，Logistic半参数回归模型即退化为普通的半参数模型。

为了给出模型中未知参数和未知函数的估计，取B样条基函数(B1(t),…,BL(t))T，其中L表示样条基的维数，L=J+r+1，J为节点个数，r为B样条基的次数，在本文中取立方样条，即r=3。因此g(t)≈γTB(t)，其中γ为L维列向量，γ=(γ1,…,γL)T。从而模型可以近似表示为：

其惩罚似然函数为：

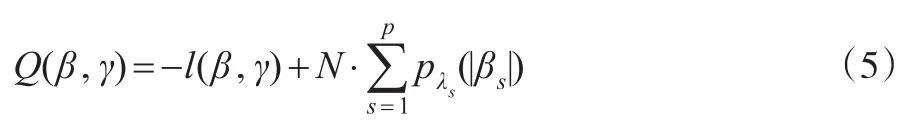
这里，λs为正则化参数，其决定对系数压缩强度的大小。l(β,γ)为对数似然函数，且：

式（6）中pλ(|·|)为惩罚函数，本文中应用的惩罚函数有：①lasso惩罚pλ(|θ|)=λ|θ|，②SCAD惩罚：

通常a=3.7，对于正则化参数以及节点个数的选取，本文中采用K折交叉验证的方法．将研究对象分成大致相等的K组，令k[i]为含有第i个个体的那一组。记与为去掉k[i]组后对β与γ的估计。则K折交叉验证得分为：

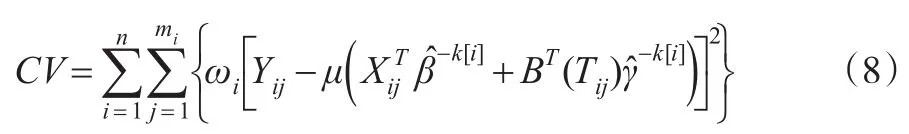
令λs=λ,s=1,…,p，极小化上述CV得分选择正则化参数λ与节点个数J。式（8）中，ωi为权重，结合纵向数据的特点，取ωi=1mi。式（8）给出的剔除个体的K折交叉验证法与传统的交叉验证法的不同之处在于，同一个体的所有不同时间点的测量数据被同时删除，这样处理的好处在于不会破坏纵向数据的组内相关性结构。本文选择固定节点位置的方式，当然也可用CV方法通过数据驱动选择节点位置，只是这样处理将导致计算的复杂度极度上升，故建议在估计过程中采用Z.Huang等（2004）中所采用的等间距样条方法，只选择节点个数，从而大大降低计算量。

2 数据模拟

对于非参数的部分，给出两种估计方法，即采用固定样条节点个数，即节点个数约为n10和用CV方法选择节点个数。考虑纵向数据半参数Logistic模型：

其中β=(5,3,8,2,0,0,0,0,0,0)T，对于协变量的选取，分两种情况进行讨论，以说明所提方法在不同情形下的数据表现。

情形1：协变量X1,…,X10相互独立，来自于均匀分布U(-1,1)，此情况是为了检验均匀设计且独立设计的情况下本文所提估计方法的数据表现。

情形2：协变量X1,…,X10相互独立，来自于混合正态分布，其中混合有三个正态分布N(0,0.1)，N(-0.9,0.1)与N(0.9,0.1)。样本来自这三个总体的概率分别为2 5,3 10,3 10，此情况是为了检验聚集设计的情况下估计量的数据表现。

针对不同的样本量n=100，n=200，n=300均生成200个数据集，用以研究收敛速度。在数据模拟中，观测时间是生成的，但存在随机缺失。观测时间生成方式为：每一个研究对象均有一个时间表{0,2,4,6,8,10,12}，并且每一个观测时刻除时刻0之外均有20%的概率缺失。再对没有缺失的时刻加上一个均匀分布U(-1,1)的随机扰动，构成最终的观测时刻表。这样生成的观测时间，每个个体的观测时刻均不相同，符合纵向数据的特点。

模型1：g(t)=sin(t)，在这种情况下，非参数的部分不能用线性模型近似，其随时间呈非线性变化。

模型2：g(t)=tsin(t)12，相比模型1，此种模型非参数部分随时间变化的特点不同于上一个模型，此模型随时间的推移其变化愈发剧烈。

模型3：g(t)≡0，此模型为参数模型，本文中将应用g(t)≡0的先验信息进行估计，并在不使用先验信息的情况下采用本文的估计方法对参数部分进行估计，用以检验当没有采用先验信息（即模型设定并不精确）的条件下的估计方法的稳健性。

模拟结果见表1至表6：

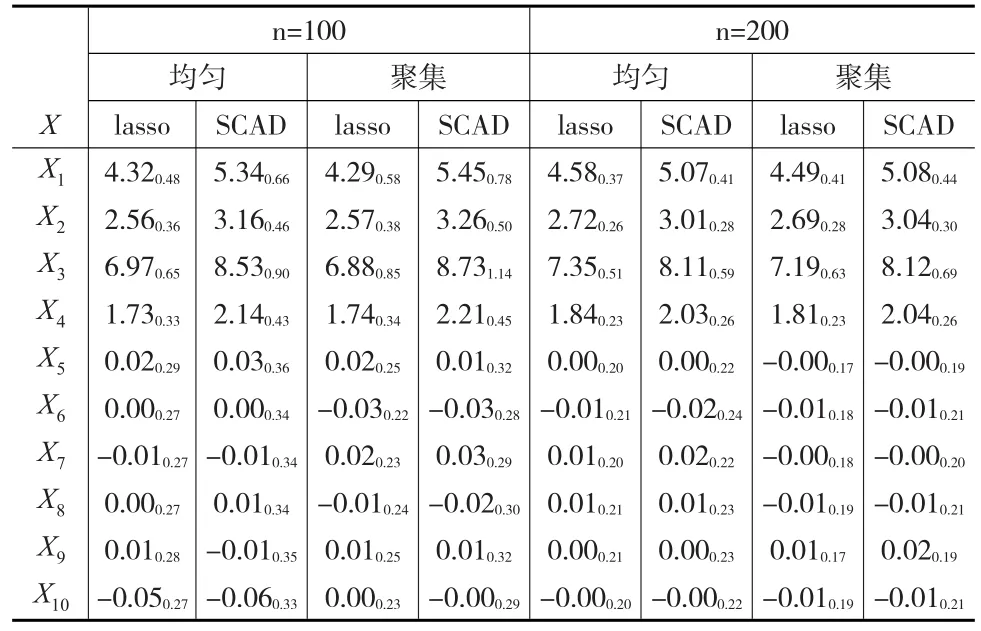
表1 模型1的变量选择结果

表2 模型2的变量选择结果

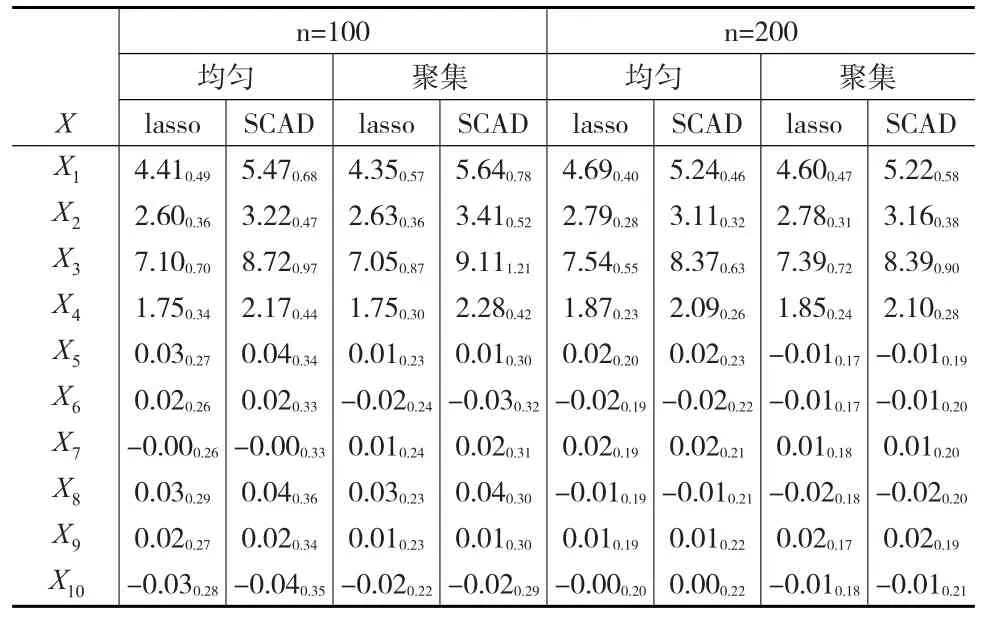
表3 模型3的变量选择结果

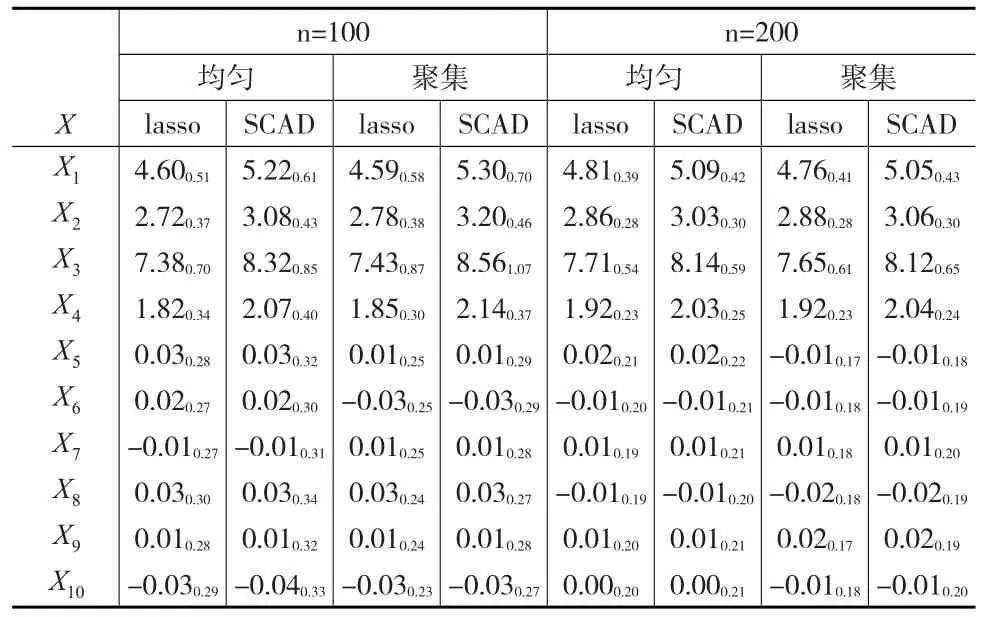
表4 模型3有先验信息(即已知g(t)≡0)时的变量选择结果

表5 模型1采用CV方法选择节点个数时的变量选择结果(样本量为100)

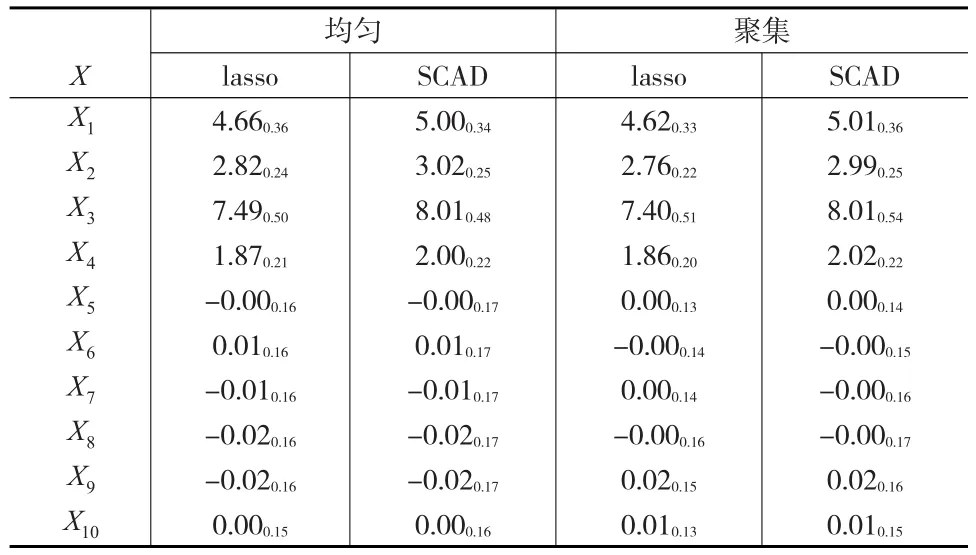
表6 模型1在样本量为300时的表现

在表1至表6中，每个格内的数据是200次模拟数据的估计均值，格中数据的下标表示估计结果的标准差。从6个表中可以看到，对于SCAD估计方法，估计结果与真实结果相差很小，SCAD估计方法的偏差小于估计量方差的12，因此可以认为SCAD方法是无偏的。SCAD方法的标准差约为非零参数的110，说明估计非常准确，特别是表6当中，对于非零参数部分，SCAD估计值与真实值之间的差值小于1%，与真实值已相当接近。对于lasso方法，其偏度大于一个标准差，说明lasso方法有偏，这与普通均值模型中lasso有偏而SCAD无偏的情况相同。观察数据可以发现：对于有正则信息的最简单情况（表4），不论是均匀设计还是聚集设计，在样本量相同的情况下对于非零系数而言，SCAD惩罚的偏度要小于lasso，方差大于lasso。但SCAD较lasso的方差增大量小于其偏度的减小量，因此从均方误差的角度讲，SCAD惩罚的均方误差小于lasso。对于零系数而言，两种惩罚方法在偏度和方差上的表现相当，SCAD方法的方差略大。当样本量相同时，不论lasso还是SCAD，均匀设计与聚集设计在偏度上的表现相当，但聚集设计的方差较大。随着样本量的增大，两种惩罚方法的偏差和方差均减小。表3中的数据表现与表4接近，表4中偏差和方差较表3来说，虽然可以看出一定程度的减小，但在采用SCAD时，在没有正则信息的情况下，估计量的偏差非常小，小于真实参数的110，因此可以认为当g(t)≡0时，采用本文所述估计方法得到的估计效果与正确设定非参数部分形式时的估计效果相差并不太大，说明文中所提方法具有很好的稳健性。

从表1与表6中还可以发现，不论是lasso方法还是SCAD方法，对于非零参数，聚集设计的方差与偏差均较大，因而聚集设计的均方误差较大，但随着样本量的增大，两种设计下的方差与偏差大小分别趋向于相同。随着样本量的增大，lasso方法与SCAD方法的标准差趋于相同，但SCAD方法的方差始终大于lasso。对于零参数，两种方法的偏度相同，均小于标准差的110，因此可以认为对于零参数来说，两种方法均是无偏的。与非零参数相同的是SCAD的方差始终大于lasso，且随着样本量的增加，两种惩罚方法的标准差趋于相同，均匀设计与聚集设计下的标准差趋于相同，但与非零参数的表现不同的是，零参数下均匀设计的标准差始终大于混合设计。故对非零参数而言，SCAD方法的均方误差对不同的样本量一致较小，对零参数一致较大。非零参数下的标准差是零参数下标准差的两倍，说明本文所提两种正则化方法确实起到了压缩零参数的作用。比较表2自身的数据，表中估计量的表现与表1相同，说明不论非参数部分是怎样的形式，文中所提估计量的数据表现均有相似的特点。

纵向比较表1、表2与表3、表4，发现对于lasso惩罚，不论理论模型是否为非参数模型，惩罚所导致的估计结果的偏差和方差大致不变，再次说明本文所提出的估计方法十分稳健。

比较表1与表5发现，不论是否采用CV方法惩罚节点个数，估计效果大致相同，CV方法的偏差较大，但方差较小，CV方法的均方误差小，但采用CV方法惩罚节点个数将急剧增加计算上的复杂度，为了节省估计时间，不建议采用交叉验证法选择节点个数，而是采用通常的方法，即节点个数约为样本数量的十分之一。

此外，对于协变量存在多重共线性的情况，估计量的方差将变大。

3 结论

本文讨论了纵向数据半参数Logistic模型估计，通过非参数函数的估计和参数部分的变量选择方法，与数值模拟发现，所提方法在有限样本下具有优良的性质。需要说明的是，在进行变量选择时，发现对于系数不为零的变量，不论协变量是聚集设计还是均匀设计，采用SCAD方法时，估计量的标准差以约为的速度缩小，而lasso方法的标准差缩小速度较慢。聚集设计的估计量方差普遍大于均匀设计。SCAD方法的偏差与均方误小于lasso，方差普遍大于lasso，SCAD方法的偏差随着样本量的增加而减小。本文所提方法具有很好的稳健性，当理论模型为参数模型，而估计时设定为本文所提模型时，估计量的表现与正确设定模型形式时相当。等间距样条节点个数选为n10是合理的，与采用CV方法选择节点个数时的表现相似，但CV方法造成计算上的负担，故不建议用CV方法。

[1]P.J.Diggle,P.J.Heagerty,K.L.Liang,S.L.Zeger,Analysis of Longitudinal Data,Oxford University Press,Oxford,2002.

[2]Liya Fu,You-Gan Wang.Efficient Parameter Estimation via Gaussian Copulas for Quantile Regression with Longitudinal Data[J].Journal of Multivariate Analysis1(2016)43.

[3]Jianqing Fan and Runze Li.New Estimation and Model Selection Procedures for Semiparametric Modeling in Longitudinal Data Analysis[J].Journal of American Statistical Association,Vol.99,No.467(2004).

[4]Jianhua Z.Huang,Colin O.Wu and Lan Zhou.Polynomial Spline Estimation and Inference for Varying Coefficient Models with Longitudinal Data[J].Statistica Sinica(2004),14.

[5]Jianqing Fan,Tao Huang and Runze Li.Analysis of Longitudinal Data with Semiparametric Estimation of Covariance Function[J].Journal of American Statistical Association(2007)Vol.102.,No.478

[6]Hong Z,Hu Y and Lian H.Variable Selection for High-Dimensional Varying Coefficient Partially Linear Models via Nonconcave Penalty[J].Metrika,Volume 76,2013,7.

[7]Jianqing Fan and Runze Li.Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties[J].Journal of American Statistical Association,96,(2001)456.

[8]Hui Zou.The Adaptive Lasso and Its Oracle Properties[J].Journal of American Statistical Association,Vol.101,No.476,(2006).

[9]Verhasselt A.Generalized Varying Coefficient Models:A Smooth Variable Selection Technique[J].Statistica Sinica(2014),24.

[10]Jun Dong,Jason P.Estes,Gang Li and Damla Senturk.A Two-step Estimation Approach for Logistic Varying Coefficient Modeling of Longitudinal Data[J].Journal of Statistical Planning and Inference(2016),174.

Variable Selection for Semi-parametric Logistic Regression Model with Longitudinal Data

Gao Xianli1,Jiang Yuying2

(1.School of Statistics,Capital University of Economics and Business,Beijing 100070,China;2.Department of Basic Courses,Beijing Institute of Graphic Communication,Beijing 102600,China)

This paper studies the estimation problems of semi-parametric logistic regression model with longitudinal data,and presents a method of estimating the unknown parameter and the unknown function.The paper also investigates the variable selection of the parametric components,and makes a comparison among different methods of variable selection.Simulation results show that the method proposed in this paper has very good estimation effects.

longitudinal data;semi-parametric logistic regression model;variable selection.

O212.7

A

1002-6487（2017）20-0026-04

国家社会科学基金资助项目（10CTJ001）；首都经济贸易大学研究生科技创新重点项目；北京印刷学院校级资助项目（Eb201606）

高仙立（1991—），男，天津人，博士研究生，研究方向：应用统计。

（通讯作者）姜玉英（1976—），女，山东济宁人，副教授，研究方向：经济统计分析。

(责任编辑/亦 民)