汽车驱动桥准双曲面齿轮时变啮合刚度计算

刘 程， 史文库， 陈志勇， 何 伟， 荣如松， 宋怀兰

(1.吉林大学 汽车仿真与控制国家重点实验室, 长春 130022；2．南京依维柯汽车有限公司车桥分公司，南京 210028)

汽车驱动桥准双曲面齿轮时变啮合刚度计算

刘 程1， 史文库1， 陈志勇1， 何 伟1， 荣如松2， 宋怀兰2

(1.吉林大学 汽车仿真与控制国家重点实验室, 长春 130022；2．南京依维柯汽车有限公司车桥分公司，南京 210028)

针对汽车准双曲面齿轮动力学系统建模中齿轮时变啮合刚度计算困难的问题，提出一种完整的基于有限元法计算准双曲面齿轮啮合刚度的计算方法。详细描述利用有限元方法计算齿轮啮合刚度理论模型，并利用此模型计算直齿渐开线齿轮啮合刚度，结果表明此方法计算结果与KUANG模型计算结果一致。利用MATALAB和CATIA建立了准双曲面齿轮三维几何模型，并在ABAQUS中建立此齿轮准静态啮合有限元模型。详细论述了由准双曲面齿轮啮合有限元分析结果后处理得到啮合刚度计算过程，并对不同载荷下齿轮啮合刚度的变化趋势进行讨论。结果表明，准双曲面齿轮啮合过程中啮合刚度随齿轮旋转位置和所加载力矩周期性变化，其变化周期等于齿轮啮合周期；当齿轮加载力增大齿轮啮合刚度平均值增大，同时啮合刚度的波动减小。

准双曲面齿轮；时变啮合刚度；三维模型；有限元分析

齿轮的运动传递误差是齿轮振动能量的主要激励，在大多数齿轮设备中会引起其它部件振动并以噪声的形式向外辐射，使人产生烦躁的感受[1]。对于汽车驱动桥主减速器中准双曲面齿轮系统，以前的研究主要集中在模拟齿轮的加工过程从而得到高精度的齿轮外轮廓，通过齿轮几何接触分析来优化齿轮几何参数以及机床加工参数，然后对准双曲面齿轮静态有限元计算齿轮齿根应力，载荷分布，运动传递误差等[2]，但是这些计算结果并不能全面的反映齿轮啮合过程中齿轮系统的振动噪声响应，许多反感的齿轮啮合噪声问题在车辆驱动桥中依然存在。为此有很多研究者建立了主减速器齿轮系统的动态响应数学模型，研究齿轮系统中各部件刚度，阻尼、惯性质量对齿轮动力学系统的影响，通过啮合刚度建立齿轮静态分析与系统动态响应之间关联[3-7]。在建立齿轮动力学系统时这三类参数中准双曲面齿轮与直齿齿轮最大的区别是齿轮啮合刚度，主要由于直齿渐开线齿轮啮合时啮合力的方向基本保持不变，已有较为成熟的计算方法和经验公式[8]，但是准双曲面齿轮几何外形和啮合过程复杂，齿轮啮合过程中啮合力的方向和啮合点位置随齿轮旋转角度和加载力大小改变而改变[9]，与直齿齿轮相比在此类齿轮啮合刚度的研究较少。

在国外，Teik等建立了准双面齿轮啮合的多自由度模型，利用一个恒定常量和三角级数来对齿轮啮合刚度近似处理。Mohammadpour等[9-10]通过专业有限元软件calyx得到准双曲面齿轮时变啮合刚度，并将齿轮啮合刚度简化三角级数形式，最后得到齿轮啮合刚度经验公式。在国内，方宗德[11]根据齿轮啮合时静态受力状态建立准双曲面齿轮动态啮合模型，但是此模型并没有考虑到齿轮啮合过程中啮合刚度的时变特点。唐进元等[12]从齿轮刚度的基本理论出发计算得到单个轮齿的啮合刚度，再由单个轮齿叠加得到多个轮齿同时啮合时的啮合刚度，此模型忽略了准双曲面啮合过程齿轮啮合力的方向随齿轮啮合位置改变而变化的影响。

以上分析可得，准双曲面齿轮时变啮合刚度在国外已经提出相应的计算方法，并将啮合刚度进行傅里叶级数近似处理，通过软件直接输出齿轮啮合刚度表达式，而实际傅里叶级数并不能完全表征齿轮的啮合刚度特性，并且具体的计算细节并未公开，而当前基于应用较多的ABAQUS或ANSYS有限元的计算准双曲面齿轮啮合刚度研究很少。在国内，真实反映准双曲面齿轮啮合特征的研究较少，同时软件calyx应用较少，在建立精确的准双曲面几何模型以及有限元模型还存在困难，为此本文提出一种完整的准双曲面齿轮时变刚度计算方法，利用当前成熟的数值计算软件MATLAB得到齿轮的齿面坐标点，然后导入到CATIA中建立准双曲面齿轮三维模型，接着利用ABAQUS软件详细说明准双曲面齿轮有限元模型建模过程，并对有限元计算结果进行后处理得到准双曲面齿轮时变啮合刚度。此齿轮啮合刚度可以应用在齿轮系统动力学分析过程中，而不需要任何其它假设，因此可以为更好预测汽车驱动桥准双曲面齿轮传动系统的动力学响应提供基础。

1 齿轮啮合刚度计算模型

1.1 齿轮啮合刚度模型数学描述

以前的齿轮啮合模型基于经验设计公式或者齿轮几何啮合分析，随着齿轮设计和分析的要求提高，对齿轮接触分析提出更高要求，因此需要对齿轮接触进行更深入研究。本文基于有限元方法建立准双曲面齿轮啮合模型，来模拟齿轮的真实运行过程。下面详细介绍齿轮啮合刚度计算基本原理。

如图1所示为基于有限元模型建立的齿轮啮合耦合模型，从啮合简图可以看出，在任意啮合时刻，大小齿轮之间有很多相互作用点。每个相互作用点之间包含了齿侧间隙和摩擦非线性因素的影响，模型不需要更多的假设条件限制，可以较精确的模拟齿轮的接触。

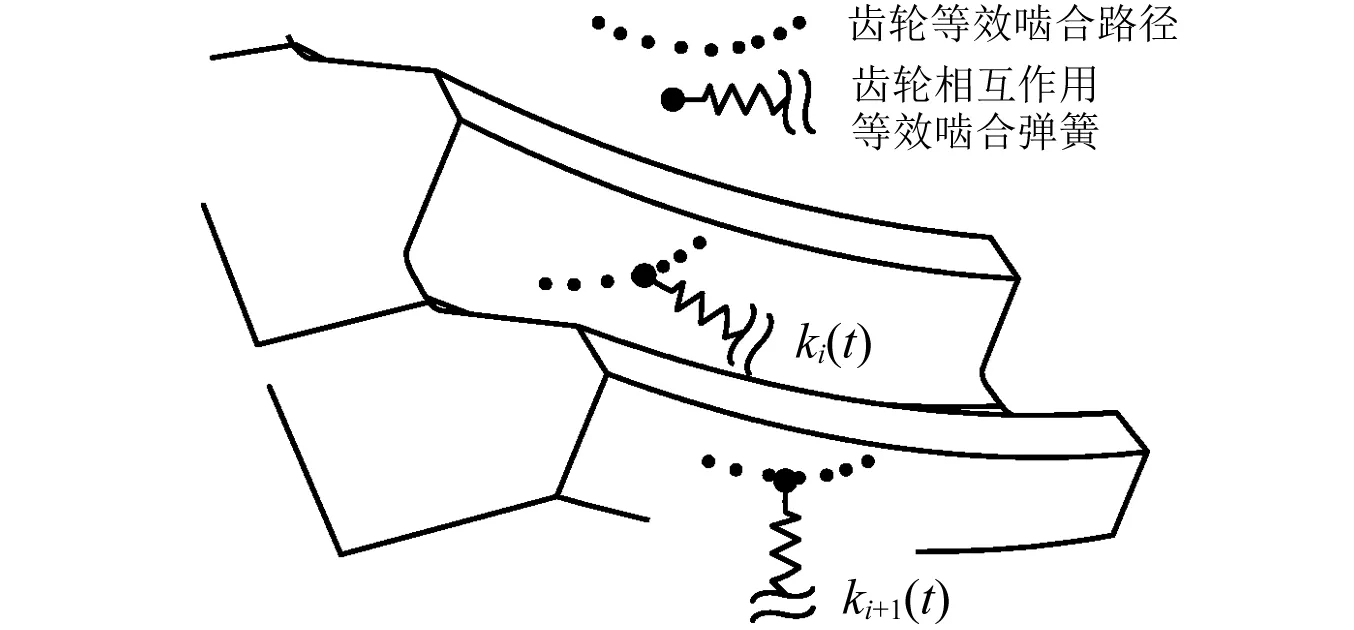
图1 准双曲面齿轮啮合模型Fig.1 Hypoid gear pair mesh model

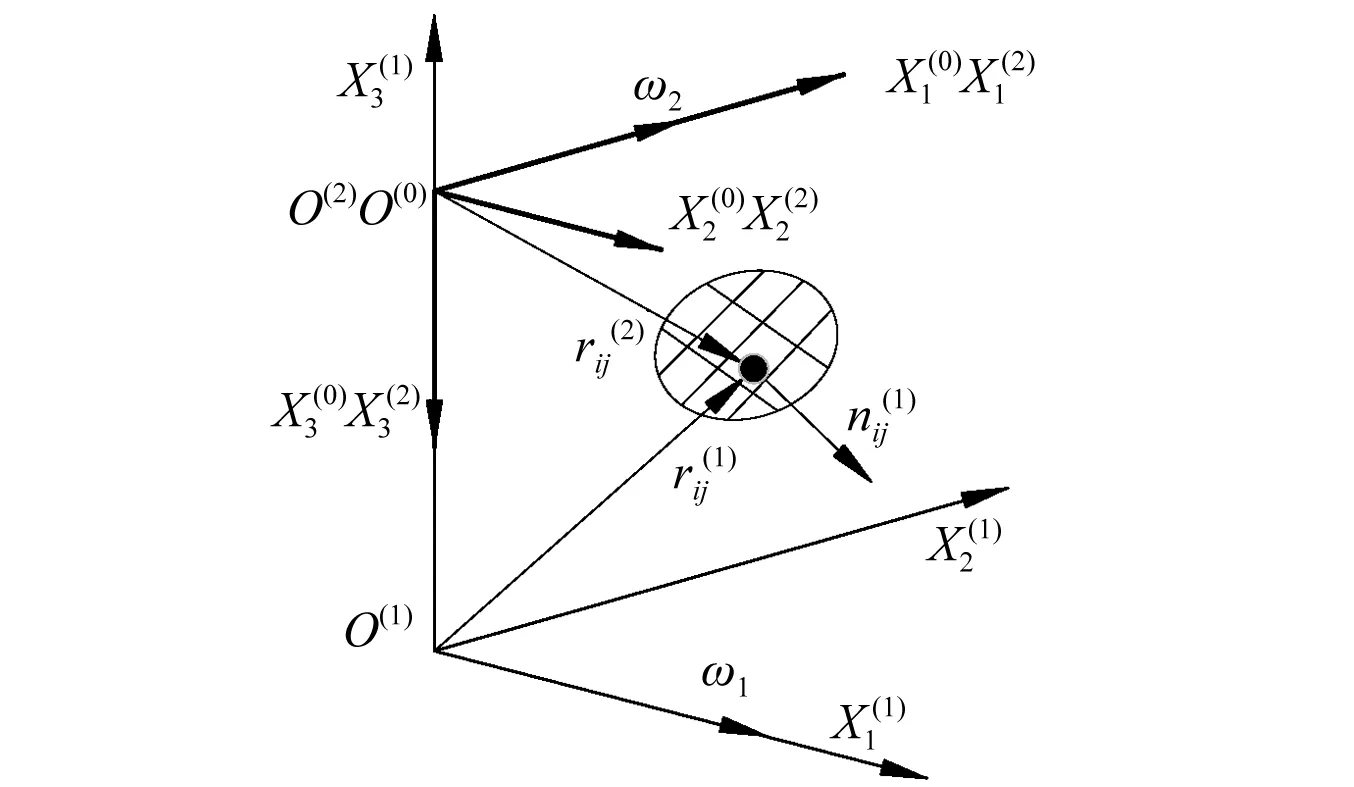
图2 齿轮啮合时接触点位置及受力关系Fig.2 The relationship for location and force of gears contact point

为获得啮合刚度，做如下参数定义：

将齿轮的接触区域离散为较小的网格单元，啮合刚度kij是齿轮的空间形状、啮合位置以及所施加力矩的函数

(1)

令Wt=ktδt，则：

(2)

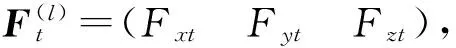
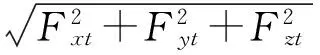
(3)

定义等效啮合点位置

(4)

任意时刻等效啮合位置作用力矩

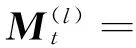
(5)

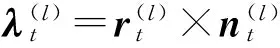
(6)

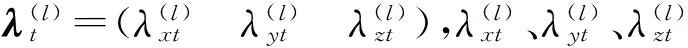
对于理想的刚性齿轮对，被驱动齿轮的位置可以通过驱动齿轮的位置除以传动比得到，即：

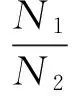
(7)

式中：θ2为大齿轮旋转角度；θ1为小齿轮旋转角度；N1为小齿轮齿数；N2为大齿轮齿数。

然而由于齿轮对总不是刚性，在接触过程中会产生变形，例如齿面弯曲，Hertzian接触变形以及齿胚变形等，被驱动齿轮的实际旋转位置和理论旋转位置的差值即为传递误差

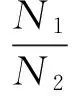
(8)

齿轮无加载的传递误差为Δθ0t，加载后传递误差ΔθLt。因此啮合刚度可定义为法向的接触力与线性变形的比值

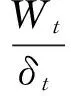
(9)

式中：δt定义为由于啮合力使得啮合齿轮面产生的等效变形。

(10)

由于此齿轮旋转轴线为x轴，绕其它轴的旋转角度接近为零，则

(11)

可以得到t时刻啮合刚度为

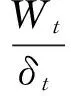
(12)

1.2 齿轮啮合刚度模型验证

选择直齿齿轮为对象对模型进行验证，这主要是由于当前直齿齿轮啮合刚度计算方法已经有广泛应用的经验公式，可以对比计算结果，而且上述啮合刚度计算方法同样适用于直齿齿轮，因此可以通过直齿齿轮刚度计算来验证上述计算方法的准确性。直齿渐开线齿轮参数，如表1所示。

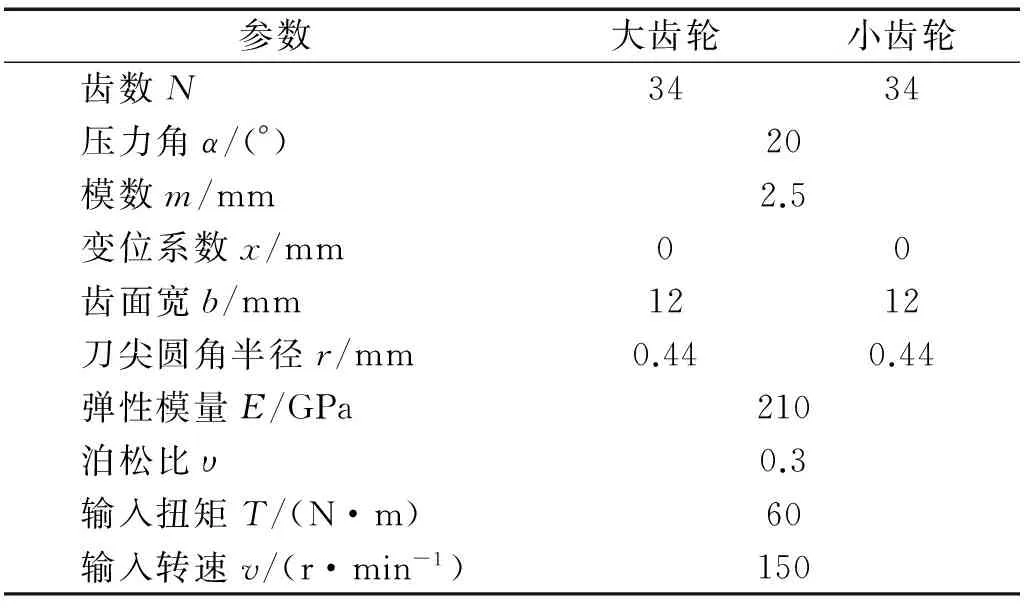
表1 直齿齿轮参数Tab.1 Straight involute gear parameters

根据齿轮参数建立有限元模型，并利用1.1节中齿轮啮合刚度计算方法获得齿轮啮合刚度，有限元计算结果和齿轮啮合刚度结果如图3，从图中可得通过本

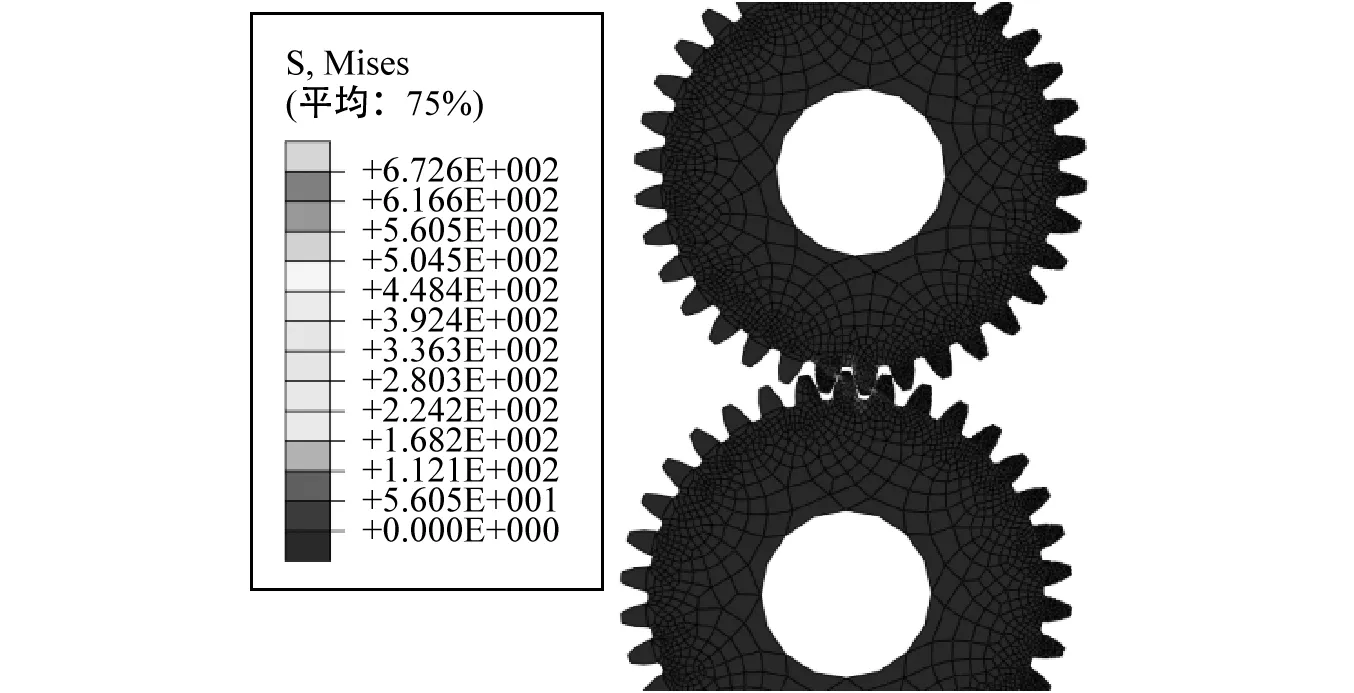
(a) 有限元计算结果

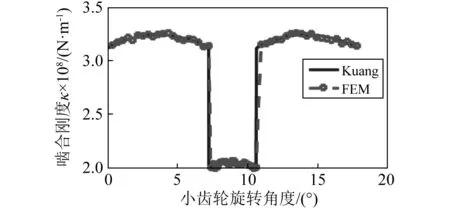
(b) 齿轮啮合刚度图3 直齿齿轮Fig.3 Straight involute gear

方法计算的齿轮啮合刚度与文献[8]中Kuang方法计算结果基本相同，有限元方法中由于考虑了齿轮接触非线性，以及摩擦非线性的影响，使得计算结果存在波动，齿轮从双齿啮合到单齿啮合出现突变使得此齿轮啮合刚度突变，导致直齿齿轮在啮合过程中会出现较大啮合冲击噪声。

2 准双曲面齿轮三维模型和有限元模型建立

2.1 准双曲面齿轮三维几何模型的建立

当前汽车用准双曲面齿轮加工方法中，一般当大轮锥角较大时即可以采用成形法加工(HFT)，也可以采用展成法加工(HGT)，当大轮锥角较小时必须采用展成法加工，小轮采用展成法加工。准双曲面齿轮齿面建模方法应用最多的是基于Litvin提出的共轭曲面法，Litvin通过研究准双曲面齿轮的生产过程，将齿轮加工过程中刀具旋转运动产生的点通过空间变换得到齿轮面上的点，对齿轮面上的离散数据点进行插值，即可生成高精度的轮齿面。齿轮面建模方法的具体流程见图4，图中u,θ为刀具旋转所形成齿面参数，ψ为齿胚旋转角度。建模过程描述如下：首先根据刀具参数得到刀具坐标矢量，然后对上述矢量进行坐标变换得到刀具所形成曲面，接着根据机床参数将刀具曲面变换到齿轮坐标系中，由准双曲面齿轮啮合原理得到啮合方程，再根据轮齿面上点必须在轮齿齿胚上，得到轮齿齿面离散点，最后对这些离散点利用非均匀B样条曲线(NURBS)进行重构，得到准双曲面大小齿轮三维数字模型。

本文以HFT准双曲面齿轮进行分析，即小齿轮采用展成法加工，大齿轮采用成形法加工，齿轮的齿胚参数和机床加工参数如表2、3所示，最后得到齿轮的三维CATIA模型如图5所示。

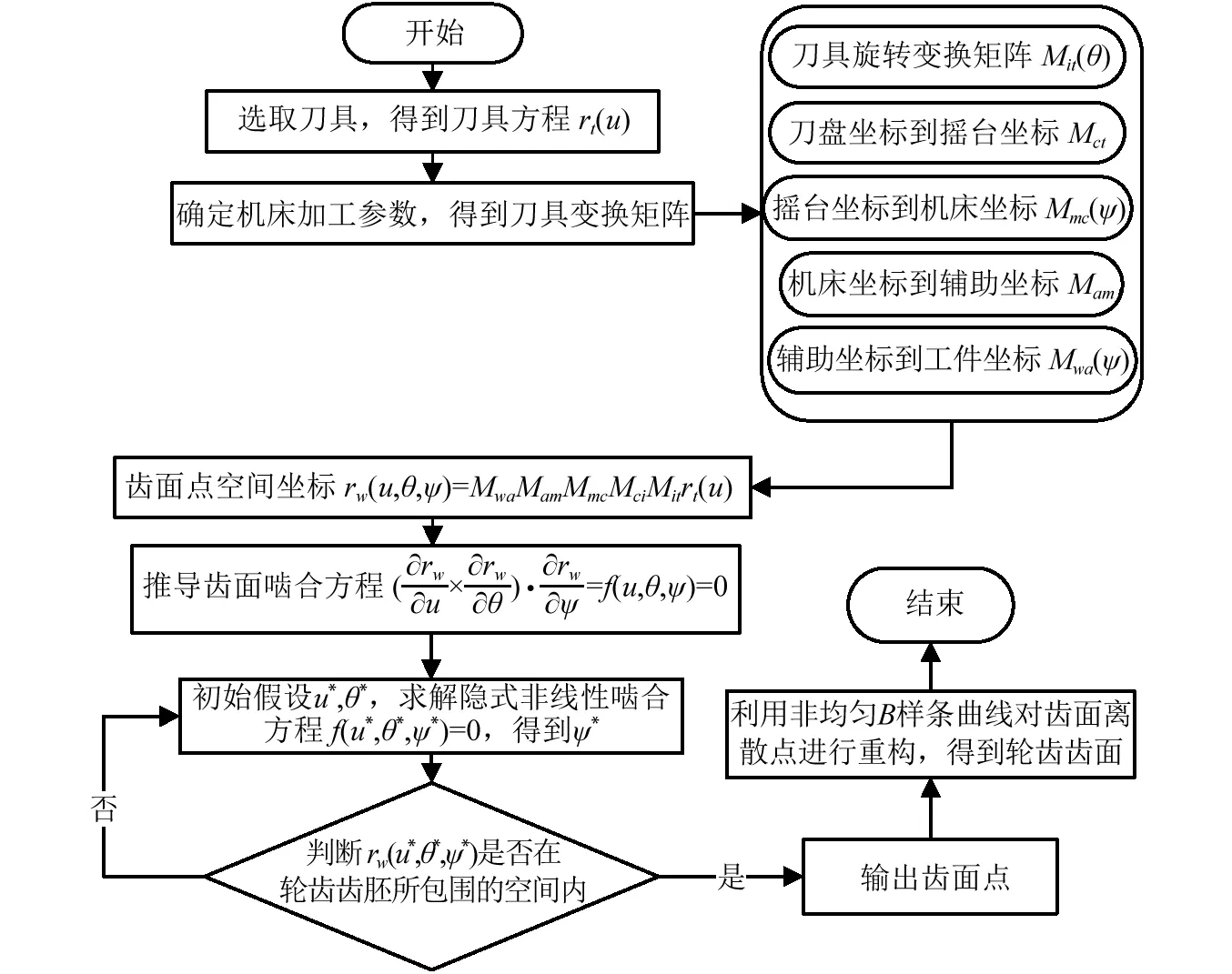
图4 准双曲面齿轮齿面建模流程Fig.4 Flowchart of hypoid gear tooth surfaces constructed表2 齿轮齿胚参数Tab.2 Gear pair bank parameters

小齿轮大齿轮模数6.861偏置距/mm-25.4旋向左旋右旋齿数843齿宽/mm44.841平均压力角22D30M22D30M外锥距/mm150.69151.26中点锥距/mm128.32130.75齿顶高/mm91.59齿根高/mm3.1710.45法向齿顶宽/mm2.743.63分锥顶点超过交叉点距离/mm0.071.08面锥顶点超过交叉点距离/mm-0.441根锥顶点超过交叉点距离/mm-6.670.05根锥角11D56M73D33M面锥角16D4M77D51M分锥角12D33M77D13M中点螺旋角45D3M33D49M

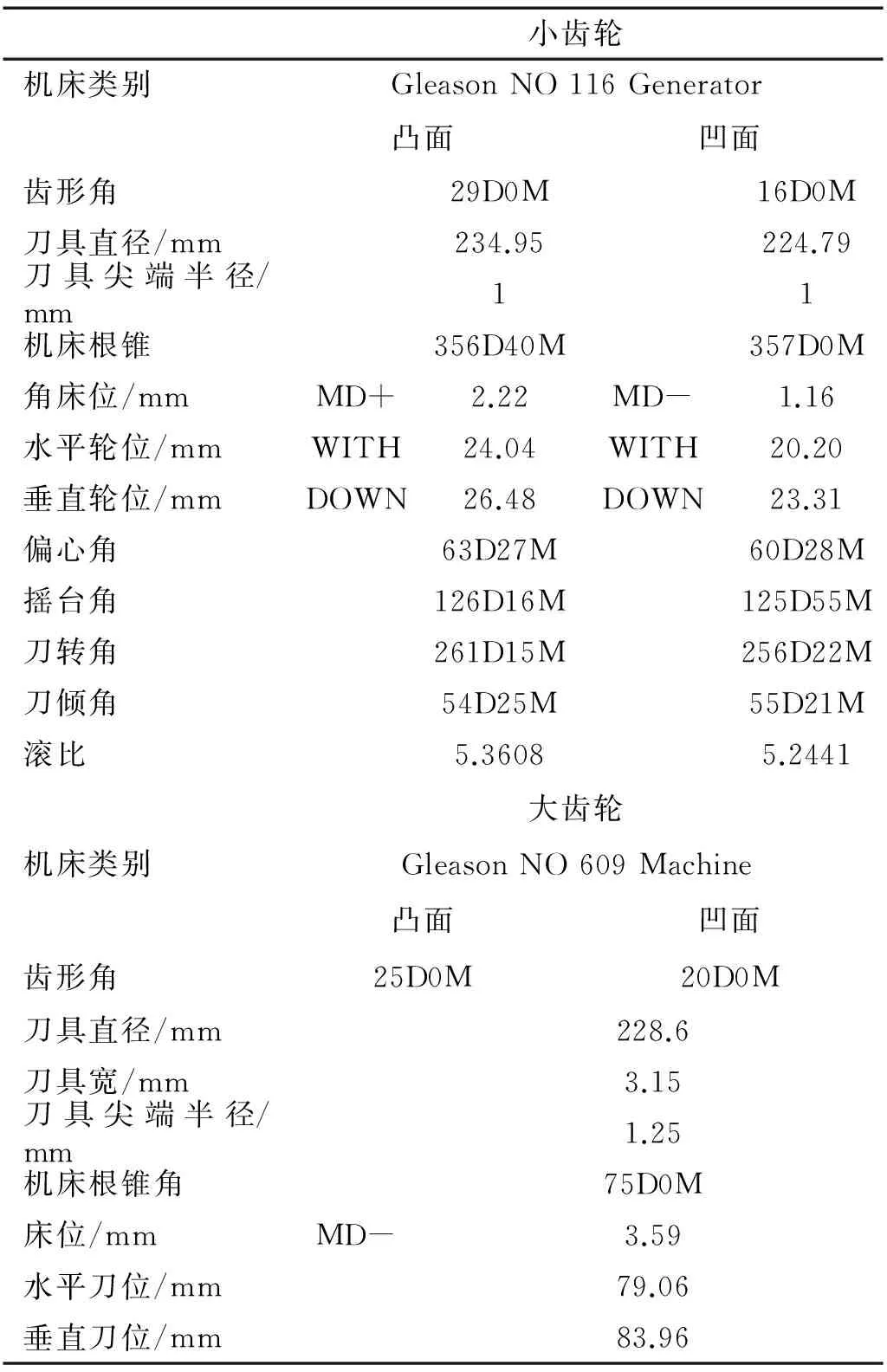
表3 齿轮机床参数Tab.3 Gear pair machine parameters

图5 准双曲面齿轮三维数字模型Fig.5 3D digital model of hypoid gear

2.2 准双曲面齿轮有限元模型建立

将上节建立的齿轮三维模型保存为*.stp格式，并导入到软件Hypermesh中进行网格划分，为了提高准双曲面齿轮啮合过程计算精度，减小齿轮几何简化对齿轮啮合的影响，本文对整个齿轮建立有限元模型，选用六面体网格，对应单元数为276 722个,节数点237 804个，最后得到此齿轮有限元网格如图6所示。

图6 准双曲面齿轮网格划分Fig.6 Hypoid gear meshing grid

先进的有限元分析软件ABAQUS在求解齿轮啮合等非线性模型上具有独特的优势，本文选取Standard/static,general求解器，对齿轮啮合过程进行准静态有限元分析。以汽车在匀速行驶工况时驱动桥齿轮啮合过程为研究对象，根据汽车行驶工况确定小齿轮输入端转速及大齿轮输出端阻力矩。

齿轮有限元求解模型的建立注意以下要点：齿轮材料的定义如表4所示，六面体网格选用具有沙漏和自锁控制的线性减缩积分单元C3D8R。为保证求解过程收敛，定义两个分析步：①载荷加载，时间长度设置为1，打开几何非线性，其它参数值为默认值；②齿轮啮合旋转，时间长度根据齿轮旋转速度及齿轮的转过角度设定，同样打开几何非线性，其它参数同上一分析步。大小齿轮之间建立面面接触轮齿对，接触属性中切向行为摩擦系数为0.1，法向行为为‘硬’接触，其它参数为默认设置。载荷加载分析步中，固定小齿轮的输入端，在大齿轮输出端上约束除绕自身轴线旋转外的所有自由度，并在输出端以斜坡线性加载行驶阻力矩。在齿轮啮合旋转分析步中，约束大小齿轮端除绕自身轴线外的所有自由度，小齿轮输入转角位移，同样以斜坡线性加载，大齿轮加载大小与前一步相同的瞬态阻力矩。为增加啮合过程的稳定性，在初始条件中定义主被动齿轮初始速度，在边界条件模块中，利用‘预定义场’对齿轮的初始啮合速度进行定义。

表4 驱动桥部件材料属性Tab.4 Material properties of drive axle components

这里先模拟汽车在40 km/h匀速行驶工况，在小齿轮输入端输入转速为9.6 rad/s，大齿输出端9 500 N·m阻力矩，如图7所示，得到大小齿轮对应的最大主应力，可以看出在齿面部位由于接触挤压出现较大压应力，接触部位近似为椭圆，在齿部位由于受到拉伸出现较大拉应力，此时齿轮有三个齿处于啮合，中间部位的齿轮齿面出现最大压应力，相应齿根部位出现最大拉应力，由有限元分析结果可知，准双曲面啮合过程中齿轮的接触始终由一端向另一端过渡，因此不会像直齿齿轮那样啮合刚度出现突变。

(a) 大齿轮

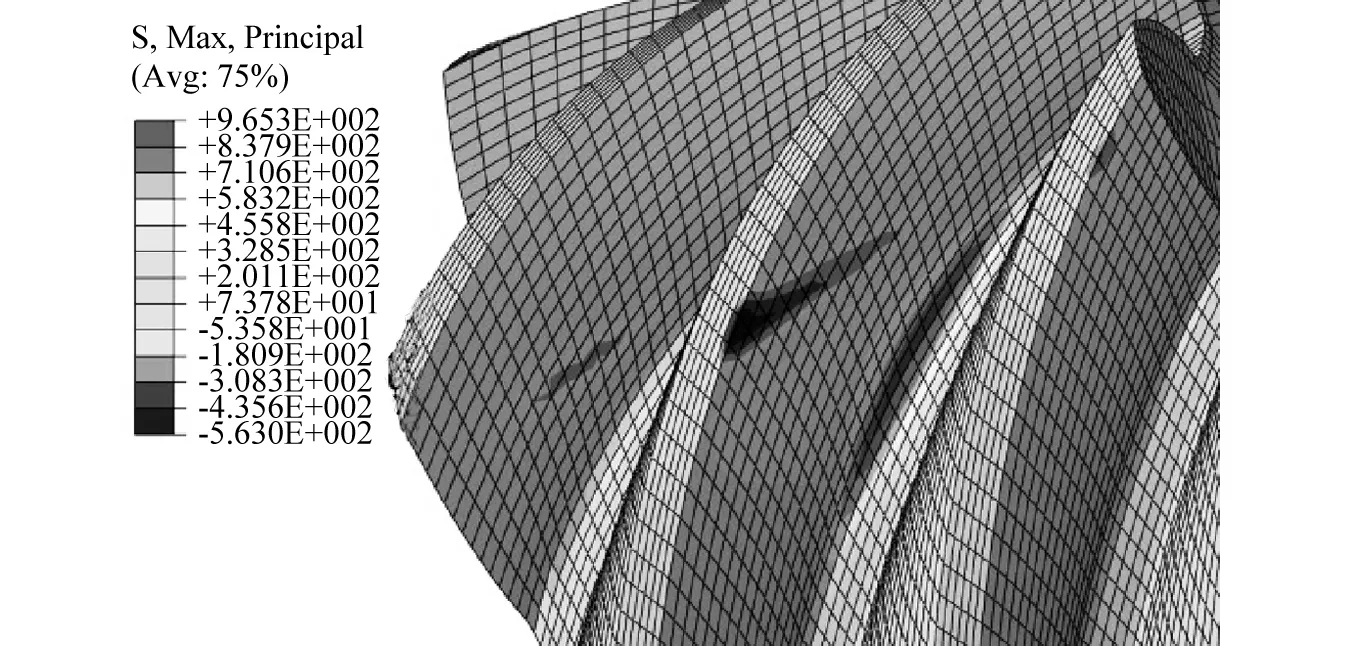
(b) 小齿轮图7 准双曲面齿轮有限元分析结果Fig.7 Hypoid gear FEM results

3 准双曲面齿轮啮合刚度计算

3.1 较小载荷下齿轮传递误差

由齿轮啮合刚度计算模型可知，在计算加载状态齿轮啮合刚度之前，首先计算无载荷下的齿轮的传递误差，本文以小载荷代替无载荷。这里施加小的旋转力矩载荷主要是由于，当前的啮合分析模型大多是基于齿轮几何啮合关系得到，此时并没有考虑齿轮加载力矩，为了对比分析结果，齿轮接触分析时应不施加任何力，但是在齿轮进行有限元接触分析时为了使轮齿对保持接触需要施加一个力，这个力矩可以非常小，这里可以取齿轮最大工作力矩的百分之一。在这个小力矩作用下，有限元接触分析基本上可以模拟齿轮无载荷作用下接触过程，可以确保在有限元分析过程中始终只有一个轮齿接触，并可以近似得到齿轮在无载荷状态下齿轮传递误差。

本文在大齿轮输出端施加10 N·m阻力矩，如图8所示为齿轮旋转过程中，三对啮合轮齿接触面等效啮合点处法向方向啮合力变化历程，接触面表示为SUF_i,其中i=1,3,5表示为大齿轮齿面，i=2,4,6表示为小齿轮齿面，大齿轮的SUF_1与小齿轮的SUF_2为啮合齿轮对，依次类推，大小齿轮的齿面法向力为作用力和反作用力，因此本文只给出大齿轮齿面的作用力，从图上可以看出每个轮齿的法向啮合力不存在重叠，齿轮始终处于单齿啮合状态，并且此时啮合力值较小。对大小齿轮啮合分析结果进行后处理可以得到齿轮啮合过程中传递误差，如图9所示，从图中可以看出，在较小载荷下齿轮的传递误差近似为抛物线，这与文献[13]实验测量的准双曲面齿轮在小载荷作用下齿轮实际传递误差一致，这是为了减小齿轮的在啮合过程中的接触冲击，齿轮设计时把齿轮无载荷时的传递误差设计为抛物线形状。

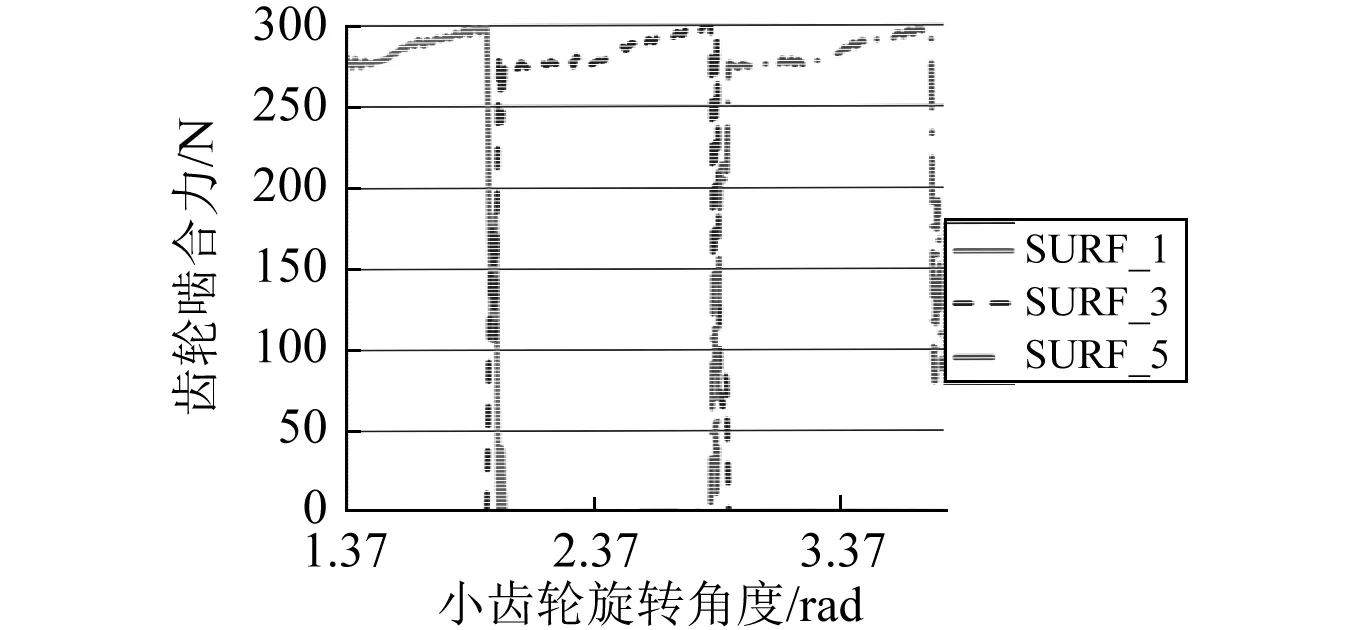
图8 小载荷作用下单个轮齿啮合力Fig.8 Gear meshing force under small loads of single teeth

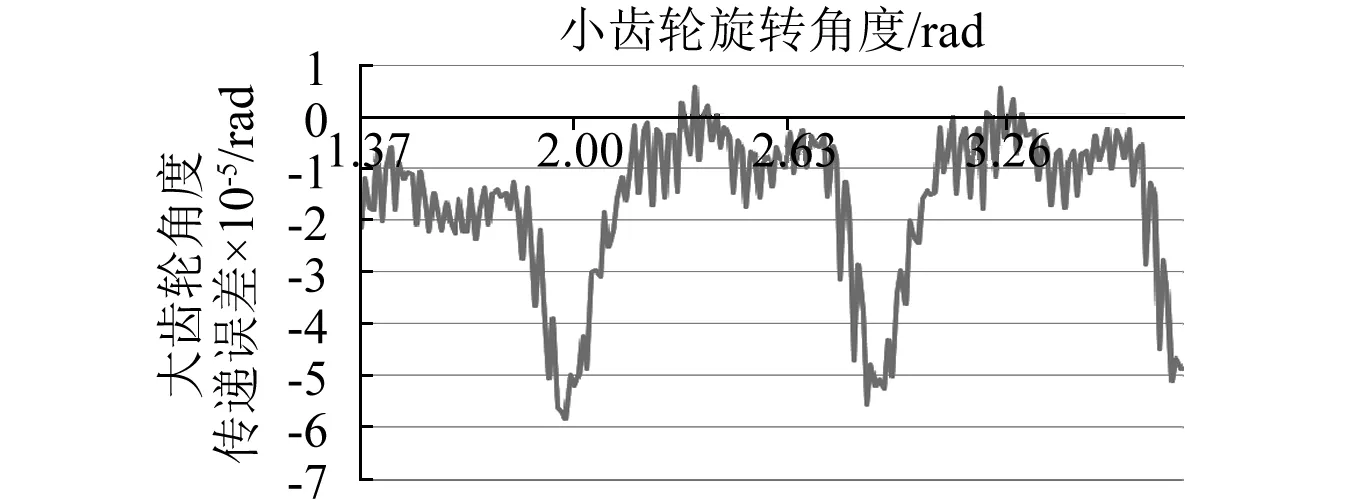
图9 小载荷作用下齿轮传递误差Fig.9 Gear transmission error under small loads

准双曲面齿轮啮合仿真方法应用最多的是齿轮几何接触分析(TCA)，他可以求得齿面的瞬时啮合点，通过齿轮接触分析可以快速得到齿轮啮合中点位置以及啮合中点的法向向量，对比TCA分析结果和在较小载荷下有限元计算结果如表5所示，有限元分析结果和TCA分析结果基本一致，表明此有限元模拟具有较高的计算精度。

表5 啮合中点坐标与啮合点法向向量Tab.5 Mean point coordinates and normal vector

3.2 齿轮加载啮合刚度

接着对齿轮进行加载状态下接触分析，在大齿轮输出端施加的阻力矩为9 000 N·m，施加转速为9.6 rad/s，如图10所示为单齿轮啮合力变化过程，SURF_i定义与图8相同，在位置1啮合位置，从图中对应位置的点划线可以看出，SURF_1对应轮齿退出啮合，SURF_5对应轮齿进入啮合，此时有三个轮齿处于啮合，同样可得位置2处，SURF_3只有两个齿轮处于啮合。与直齿齿轮不同，由于准双曲面齿轮啮合力的方向随齿轮的旋转角度变化而变化，不同时刻处于啮合的相邻轮齿啮合力方向不同，任意时刻所有齿轮的啮合力并不能由处于啮合齿轮的法向啮合力简单数值相加。对处于同一时刻齿轮啮合力需进行矢量相加，最后可得如图11所示任意啮合时刻对应的齿轮法向啮合力，从图中可以看出啮合力的大小随齿轮旋转周期性变化。

图10 大载荷作用下单个啮合齿轮啮合力Fig.10 Gear meshing force under large loads of single teeth

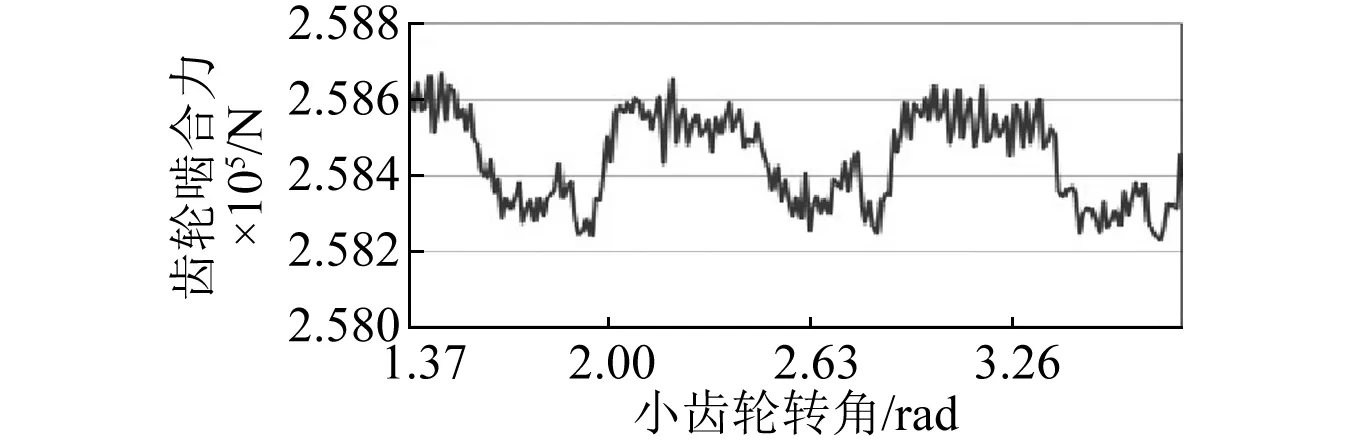
图11 大载荷作用下齿轮等效啮合力Fig.11 Gear equivalent meshing force under large loads

大齿传递误差如图12所示，可以看出齿轮的传递误差表现为周期性变化，同样保持为抛物线形状，与小载荷时齿轮传递误差相比，大载荷对应的齿轮传递误差相应向下平移，而且大载荷对应齿轮传递误差波动要比小载荷要小。因为大载荷作用下齿轮齿胚以及齿面接触产生加大变形，使得传递误差均值增大，而且由于所加载的力增大，齿轮的接触更为平稳使得大载荷作用下齿轮的啮合误差波动减小。

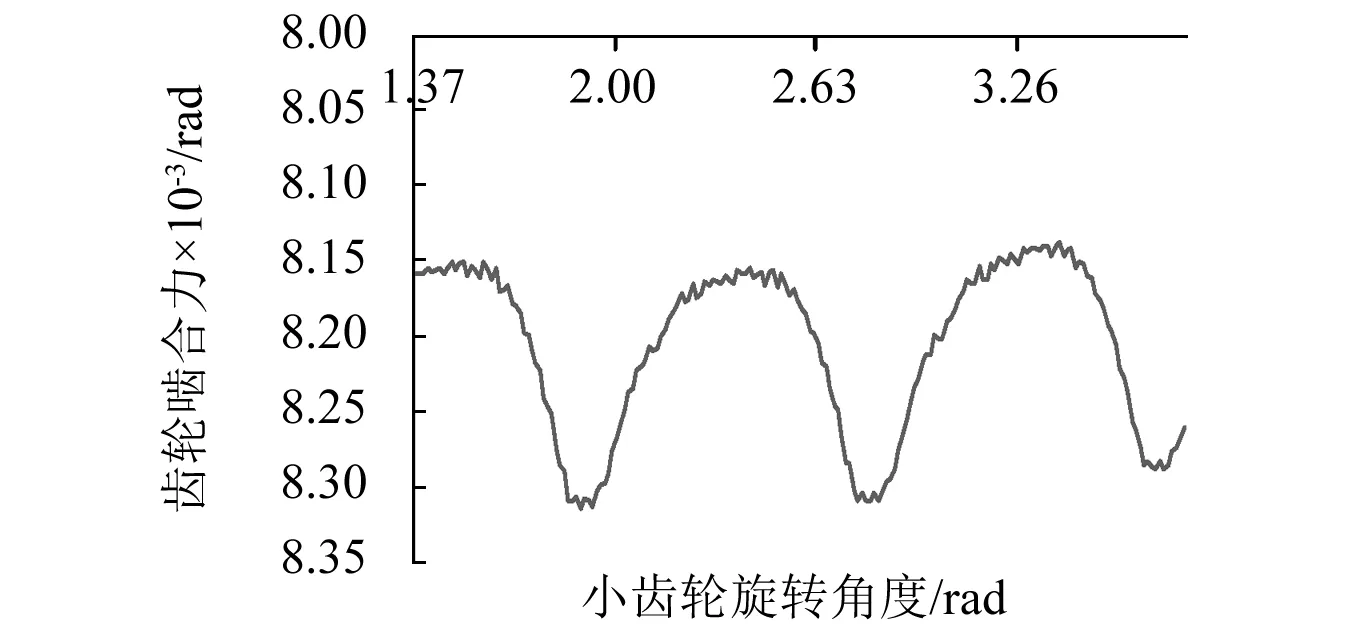
图12 大载荷作用下大齿轮传递误差Fig.12 Gear transmission error under large loads

由齿轮力、静态传递误差、加载传递误差等数据代入式(12)中即可齿轮啮合刚度，图13为啮合刚度计算结果，从图中可以看出齿轮的啮合刚度周期性变化，啮合刚度变化周期与齿轮啮合力以及齿轮传递误差变化周期相同，此周期等于齿轮啮合周期。选用齿轮啮合刚度最大时作为啮合刚度起始点，两红色点划线之间部分为一个啮合周期，在这个周期内齿轮的啮合刚度先变小，然后基本保持恒定大小，再缓慢减小，最后快速上升，接着进入下一个齿轮啮合周期。与直齿齿轮啮合过程中刚度变化趋势不同，准双曲面齿轮啮合刚度不会发生突变，这样可以使齿轮平稳接触，减小啮合冲击。

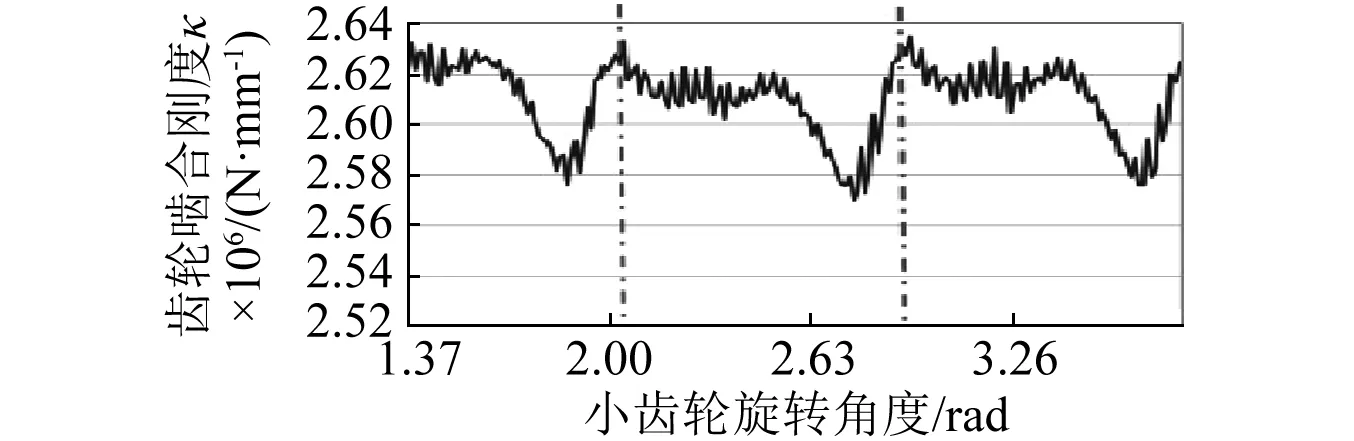
图13 大载荷作用下齿轮啮合刚度Fig.13 Gear meshing stiffness under large loads

3.3 不同载荷下准双曲面齿轮啮合刚度对比

下面对比当齿轮的受到的载荷不同时，齿轮啮合刚度变化规律。这里大齿轮分别加载1 000 N·m、3 000 N·m、5 000 N·m、7 000 N·m阻力矩与上节输入的9 000 N·m阻力矩进行对比，刚度计算结果对比如图14，从图中可以看出随着齿轮所加载力矩增加，齿轮的啮合刚度增加，同时齿轮啮合刚度波动幅值减小。主要是由于齿轮加载力增加，齿轮的啮合重合度增加，使得齿轮啮合时啮合冲击减小。同时啮合力增加使得齿轮齿胚变形增大，啮合刚度平均值增大。

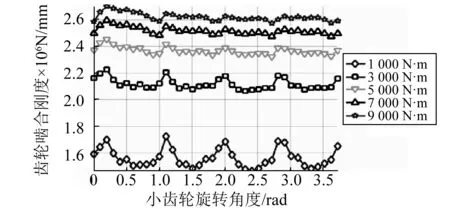
图14 不同载荷齿轮啮合刚度Fig.14 Gear meshing stiffness under different loads

4 结 论

针对准双曲面齿轮时变啮合刚度计算中遇到的困难，本文提出了完整的真实反映齿轮啮合状态的通用建模方法，并得到准双曲面齿轮啮合刚度：

(1)详细描述了通过有限元法计算齿轮啮合刚度通用计算模型，并通过直齿渐开线齿轮验证此方法的有效性。

(2)详细描述了准双曲面齿轮三维几何模型建模过程，并建立了准双曲面齿轮准静态啮合ABAQUS有限元模型。

(3)对有限元计算结果进行处理得到准双曲面齿轮啮合刚度，结果表明此齿轮啮合刚度周期性变化，变化周期为齿轮啮合周期。不同载荷的啮合刚度对比结果表明，齿轮啮合刚度随载荷增加，平均值增大，波动减小。计算所得刚度可直接应用于此准双曲面齿轮动力学系统建模分析中。

[1] KARAGIANNIS I, THEODOSSIADES S. An alternative formulation of the dynamic transmission error to study the oscillations of automotive hypoid gears[J].AMSE Journal of Vibration and Acoustics,2014, 136 (2)： 011001(1-11).

[2] LITVIN F L, FUENTES A.Gear geometry and applied theory[M]. New York: Cambridge University Press, 2004.

[3] WANG H B, LIM T C. Analysis of the mesh characteristics of hypoid gear pair dynamics[C]// ASME 2003 Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Chicago, IL：DETC2003-48053，2003.

[4] WANG Y W, LIM T C.Torque load effects on mesh and dynamic characteristics of hypoid geared system[C]// ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference IDETC/CIE 2013. Portland, OR： DETC2013-13594，2013.

[5] 王立华. 汽车螺旋锥齿轮传动耦合非线性振动研究[D]. 重庆: 重庆大学, 2003.

[6] 杨宏斌,高建平,方宗德,等. 准双曲面齿轮非线性振动分析[J]. 汽车工程,2000,22(1)： 51-54.

YANG Hongbin,GAO Jianping,FANG Zongde,et al.Non-linear dynamics of hypoid gears[J].Automobile Engineering, 2000,22(1)： 51-54.

[7] 冯治恒. 螺旋锥齿轮多体多自由度非线性动力学研究[D].重庆：重庆大学,2010.

[8] KUANG J H, LIN A D. The effect of tooth wear on the vibration spectrum of a spur gear pair[J]. Journal of Vibration and Acoustics,2001,123(7): 311-317.

[9] MOHAMMADPOUR M, THEODOSSIADES S, RAHNEJAT H. Multiphysics investigations on the dynamics of differential hypoid gears[J]. Journal of Vibration and Acoustics,2014,136(8): 041007(1-15).

[10] KARAGIANNIS I, THEODOSSIADES S, RAHNEJAT H. On the dynamics of lubricated hypoid gears[J]. Mechanism and Machine Theory, 2012,48 (1) : 94-120.

[11] 方宗德. 准双曲面齿轮传动的动载荷计算[J]. 汽车工程,1994,16(2): 92-97.

FANG Zongde. Dynamic load calculation of hypoid gear [J].Automobile Engineering, 1994,16(2): 92-97.

[12] 唐进元, 浦太平.基于有限元法的螺旋锥齿轮啮合刚度计算[J]. 机械工程学报,2011,47(11): 23-29.

TTANG Jinyuan，PU Taiping. Spiral bevel gear meshing stiffness calculations based on the finite element method [J]. Journal of Mechanical Engineering, 2011,47(11): 23-29.

[13] GOSSELIN C, GUERTIN T, REMOND D, et al. Simulation and experimental measurement of the transmission error of real hypoid gears under load[J]. AMSE Journal of Mechanical Design,2000, 122 (3): 109-122.

Acalculationmethodforthehypoidtimevaryingstiffnessoftheautomobiledriveaxle

LIU Cheng1, SHI Wenku1, CHEN Zhiyong1, HE Wei1, RONG Rusong2, SONG Huailan2

(1. State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China;2. Axle Branch of Naveco Company Ltd.，Nanjing 210028，China)

In the automotive driver axle hypoid gear meshing process, it is difficult to calculate the time varying mesh stiffness. To solve this problem, a complete calculation method was proposed, which is based on the finite element method. Firstly, a detailed process was described for the gear mesh stiffness calculation mathematical model, by the finite element method, and the meshing stiffness of the straight involute gear was calculated using this model. The results indicate that this method is consistent with the results of the Kuang model. Secondly, a three-dimensional model of hypoid gears was built by MATALAB and CATIA, and a quasi static engagement finite element model was established in ABAQUS software for that. Finally, the calculation process has been discussed for the gear mesh stiffness, and the gear mesh stiffness variations were analyzed under different loads. The results show that the gear mesh stiffness cycle varies with the gear rotating and the load torque changing, and the period of gear meshing stiffness is equal to the period of gear meshing. The average value of the gear meshing stiffness increases and the fluctuation reduces when the gear load torque increases.

hypoid gear; time varying mesh stiffness; three-dimensional model; finite element analysis

国家自然科学基金资助项目(51205158)；中国博士后科学基金面上资助项目(2013M541294)

2016-06-27 修改稿收到日期： 2016-08-15

刘程 男， 博士生， 1985年生

史文库 男， 博士， 博士生导师，1960年生

U463.218+.1

A

10.13465/j.cnki.jvs.2017.20.036