SH波作用下桩-液化土-结构体系的水平振动特性

邵艳丽， 方晓雯， 杨 骁

(上海大学 土木工程系， 上海 200072)

SH波作用下桩-液化土-结构体系的水平振动特性

邵艳丽， 方晓雯， 杨 骁

(上海大学 土木工程系， 上海 200072)

将桩等效为Timoshenko梁，上部结构等效为单自由度弹簧质量块，基于桩-土相互作用的Winkler模型，研究了在垂直入射简谐SH波作用下桩-液化土-上部结构耦合体系的水平振动特性。考虑土体的自由场位移、上部结构的平动和转动惯性以及和桩轴向压力的二阶效应，建立了单桩-液化土-上部结构耦合体系的边值问题，得到桩变形和上部结构运动的解析解。数值分析了几何和物理等参数对桩头和上部结构位移放大因子和动力放大因子的影响，结果表明：单桩-液化土-上部结构体系存在明显的共振现象，且土体自由场位移对桩头和上部结构的位移放大因子影响显著；随着上部结构刚度的增加，桩-液化土-上部结构体系的基频增大，位移放大因子峰值减小；随着土体液化的发展，单桩-液化土-上部结构系统基频和动力放大因子逐渐减小。

SH波；液化土；桩-土-结构相互作用；Winkler模型；动力特性；解析解

桩基础在大跨度桥梁、核电站和高层建筑等领域的广泛应用使得桩-土-结构相互作用研究受到众多学者的关注，成为地震工程、建筑工程以及桥梁工程等领域的热点问题之一[1-2]。大量的地震灾害调查表明：地震荷载引起的饱和砂土或粉土液化是结构破坏的主要原因之一[3-5]。相比于非液化土与桩基动力相互作用的理论体系，液化土体与桩基的相互作用理论、分析方法等研究尚未成熟，若干问题亟待解决[6-8]。

在揭示桩-液化土-上部结构相互作用机理的土体液化震害调查和试验研究基础上[9-13]，基于桩-土相互作用的Winkler模型，Bhattacharya等[14-15]将桩和上部结构分别等效为Euler-Bernoulli梁和刚体，忽略土体自由场位移，研究了单桩-土-上部刚性结构体系的动力特性，并与离心试验结果进行了比较，而杨骁等[16]研究了液化土侧向扩展对桩变形影响。杨骁等[17]将桩等效为Rayleigh梁，忽略土体自由场位移，研究了成层液化土中单桩-土-上部结构体系的水平振动特性，而段玮玮等[18]利用精确有限元法研究了液化土中Timoshenko桩的自由振动与稳定性问题。Varun等[19]建立了桩-土相互作用的非线性动力Winkler模型，研究了液化土体中桩-土-上部结构体系的动力行为，而Ni等[20]提出了一种新的p-y曲线，分析了不同应力状态下液化土中桩的横向承载力。Mokhtar等[21]利用三维有限元软件DIANA研究了土体沉降、桩径、震级和地震持续时间等对液化场地中桩基础性能的影响，而Tang等[22]基于土体弹塑性动力本构，试验和数值研究了液化土中桩-土-上部结构动力相互作用。

在桩-土-上部结构动力相互作用的解析研究中，通常将上部结构等效为固定于桩顶的刚体，这样忽略了上部结构柔性对体系动力行为的影响，并且，若干学者同时忽略了地震自由场位移的影响。然而，地震中土体自由场位移和上部结构柔性将影响桩-土-结构体系的动力行为，特别地，由于高耸上部结构或高架路桥的上部结构具有较大的柔性，此时，上部结构柔性对体系的动力特性的影响将不可忽略。为此，本文基于桩-土相互作用的Winkler模型，将桩和上部结构分别等效为Timoshenko梁和单自由度弹簧质量块，考虑土体自由场位移、上部结构平动和转动以及桩轴向压力的二阶效应，建立了桩底基岩垂直入射简谐SH波作用时液化土层中的单桩-土-上部结构体系的边值问题，求得桩桩变形和上部结构运动的解析解，通过与相关实验结果的比较，验证了理论模型及其解析解的合理性和有效性。在此基础上，分析了单桩-液化土-上部结构系统几何和物理参数等对桩头和结构位移放大因子和动力放大因子的影响。

1 问题的描述及土体自由场振动

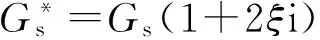
(a)桩-土-上部结构体系 (b)单桩-土-单自由度弹簧 模型 质量体系图1 桩-土-上部结构体系的物理模型和分析模型Fig.1 Physical and analysis models of pile-soil-superstructure system

显然，在基岩处简谐SH波ur(t)=u0Leiωt作用下，土体自由场的稳态振动仅存在y方向的位移分量，且此位移分量仅依赖于坐标x，而与坐标y和z无关。记土体y方向的位移为uy=(x,y,z,t)=uf(x,t)。由弹性波动理论可得土体自由场的运动方程和边界条件为[24]

(1)

记土体自由场振动相对于基岩的位移为ws(x,t)，即uf=ur+ws，且设ws(x,t)=Lus(x)eiωt，将其代入式(1)，并利用分离变量法可得

(2)

其中，fn(x)=cos(αnx/L)

(3)

2 单桩-土-上部结构体系的振动

将桩等效为Timoshenko梁，且假定为小挠度变形，考虑轴向压力N的二阶效应，记液化土层和未液化基层中桩的挠度分别为w1(x,t)和w2(x,t)，而其截面转角分别为φ1(x,t)和φ2(x,t)，则桩的运动方程为[25]

(4)

式中，wj0=wj-uf为桩相对于土层的位移。

由于将上部结构等效为单自由度弹簧质量块，若弹簧的伸长为Δ(t)，则质量块的水平位移为wb=w1(0,t)+Δ(t)。记桩顶的剪力和弯矩分别为FS1(0,t)和M1(0,t)，则质量块平动和转动运动方程为

(5)

利用物理方程[25]

(6)

可得桩头边界条件为

(7)

且

(8)

假定桩底固定于基岩中，且随基岩振动，则桩底边界条件为

φ2=0,w2=ur(t)=u0Leiωt,x=L

(9)

液化土层与未液化基层交界处桩的连接性条件可表示为

(10)

对于桩的稳态振动，可设wj(x,t)=uj(x)eiωt和φj(x,t)=θj(x)eiωt，且引入如下无量纲量和参数

(11)

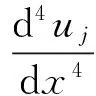
(12)

(13)

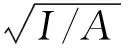
(14)

(15)

而桩横截面转角由下式确定

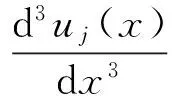
(16)

其中，

β=χG,χ=[(G+N-ω2r2)(G+N)]-1

(17)

(18)

显然，式(12)有通解

(19)

其中，Ci(i=1,2,…,8)为待定系数，且

(20)

(21)

而

(22)

于是，由式(16)可得

(23)

其中，

(24)

将式(19)和式(23)代入式(13)中，可得确定待定系数Ci(i=1,2,…,8)的线性方程

[A]{C}={b}

(25)

其中，[A]为8×8系数矩阵，{b}={b1,b2,…,b8}T为常矢量，而{C}={C1,C2,…,C8}T，由于篇幅所限，这里不给出[A]和{b}的具体表达式。

求得{C}=[A]-1{b}后，可得无量纲桩头位移为

ut≡D(ω)=u1(0,ω)

(26)

而上部结构的无量纲位移为

(27)

3 数值结果与分析

3.1 理论预测值与实验结果比较

Bhattacharya等[14,27]利用离心机试验研究了桩基底土体承受水平简谐SH波作用单桩-完全液化土土-结构体系的动力行为。试验中上部结构为固定在桩头质量Mb=0.55 kg、惯性矩Jb=1.738×10-4kg·m2的刚性块；桩为内径和外径分别为8.5 mm和9.3 mm、长L=189 mm的铝合金空心圆柱，其弹性和剪切模量分别为E=70 GPa和G=26.5 GPa，泊松比ν=0.3，线质量密度m=0.3 g/mm，剪切修正系数κ=0.532 3[25]，横截面回转半径和惯性矩分别为r=3.1 mm和I=110.96 mm4，且桩承受轴向压力N=275 N。

试验中未液化基层土的反力系数k2=3.72 MPa，阻尼c2=2 836.09 N·s/m2，液化土阻尼为未液化土阻尼的11%[28]，即阻尼c1=311.97 Ns/m2，取液化系数βL=5.8%[17]，即k1=βLk2=0.216 MPa，满足砂土液化系数0.02≤βL=k1/k2≤0.1[26]；土体剪切模量Gs=7.59 MPa，泊松比νs=0.32，滞后阻尼比ξ=0.05，体密度ρs=1 959 kg/m3。

定义桩头动力放大因子(DynAFP)和位移放大因子(DisAFP)分别为[14,27]

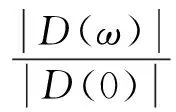
(28)

以及结构动力放大因子(DynAFB)和位移放大因子(DisAFB)分别为

(29)

取无量纲侧向刚度k=109以模拟上部结构在桩头刚性固定的情形，图2给出了当土层完全液化，即l=1时，上述物理和几何参数下桩头动力放大因子ηp随激励频率ω的响应，其中实线为考虑土体自由场位移，即us(x)≠0时单桩-土-上部结构体系的桩头动力放大因子，虚线为忽略土体自由场位移，即令us(x)=0时单桩-土-上部结构体系的桩头动力放大因子，而“*”为试验结果。可见，土体自由场位移将降低桩头动力放大因子ηp，且相比于忽略土体自由场位移时桩头动力放大因子ηp，考虑土体自由场位移的桩头动力放大因子ηp更接近试验结果。

图2 土层完全液化时理论值与实验结果的比较Fig.2 Comparisons between theoretical results with the experiment ones when soil is liquefied completely

3.2 参数分析

仍采用上述物理和几何参数，且取上部结构侧向刚度kb=27.611 kN/m[29]，即无量纲侧向刚度kb0=kbL3/EI=24，图3给出了忽略土体自由场位移时，不同土体液化深度l下桩头位移放大因子γp随无量纲激励频率ω的响应。可见，随着液化深度l的增大，即土体软化程度的增加，体系基频逐渐减小，但桩头位移放大因子γp峰值出现先增加后减小的现象，需要注意的是，当液化深度l>0.5时，体系基频几乎不变。另外通过观察图3(b)可以发现体系第二固有频率随液化深度的增加而减小缓慢，对应的位移放大因子γp峰值随l的增加而减小。图4给出了忽略土体自由场位移，上部结构刚性固定于桩头(k=109)时，不同土体液化深度l下桩头位移放大因子γp随无量纲激励频率ω的响应。比较图3和图4可以发现，将上部结构等效为单自由度弹簧质量块体系比固定于桩头的刚性质量块体系的位移放大因子γp峰值偏大、基频ω1偏小，特别是当激励频率ω处于2～8范围内时，单自由度弹簧质量块体系依然会发生共振，而固定于桩顶的刚性质量块体系几乎不振动。

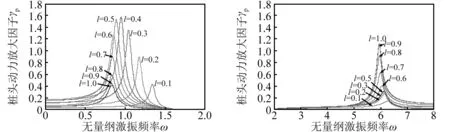
(a) 频率范围0～2 (b)频率范围2～8图3 us(x)=0时桩头位移放大因子γp随激励频率ω的响应Fig.3 Response of the DisAFP γp vs. exciting frequency ωwhen us(x)=0

图4 us(x)=0且上部刚性结构时桩头位移放大因子γp随激励频率ω的响应Fig.4 Response of the DisAFP γp vs. exciting frequency ω for rigid-fixed superstructure and us(x)=0

图5和图6分别给出了考虑土体自由场位移，将上部结构分别等效为单自由度弹簧质量块和固定于桩头刚性质量块时，不同液化深度l下桩头位移放大因子γp随激振频率ω的响应。可见，其总体变化趋势与不考虑自由场位移的情形相同，考虑土体自由场位移时第二固有频率ω2对应的桩头位移放大因子γp峰值随液化深度变化缓慢，且在ω=7附近的值要大于不考虑土体自由场位移的情况。

(a) 频率范围0～2 (b) 频率范围2～8图5 us(x)≠0时，桩头位移放大因子γp随激励频率ω的响应Fig.5 Response of the DisAFP γp vs. exciting frequency ω when us(x)≠0

图6 us(x)≠0且上部刚性结构时，桩头位移放大因子γp 随激励频率ω的响应Fig.6 Response of the DisAFP γp vs. exciting frequency ω for rigid-fixed superstructure and us(x)≠0

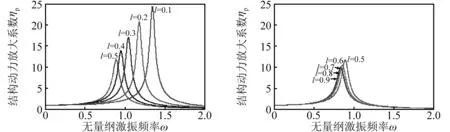
图7给出了考虑或忽略土体自由场位移，上部结构等效为单自由度弹簧质量块时不同液化深度l下桩头动力放大因子ηp随无量纲激励频率ω的响应。可见，土体自由场位移对桩头动力放大因子ηp几乎无显著影响，当l<0.5时，液化深度l对桩头动力放大因子ηp和体系基频ω1影响显著，但当l>0.5时，桩头动力放大因子ηp和体系基频ω1基本不随液化深度l而变化。另外，计算发现，相比于固定于桩头的刚性质量块体系，单自由度弹簧质量块体系的频率ω1偏小，动力放大系数峰值偏大ηp，但总体变化趋势相同。

图8和图9分别给出了考虑或忽略土体自由场位移时，不同土体液化深度l下结构位移放大因子γb和结构动力放大系数ηb随无量纲激励频率ω的响应。可见，随着液化深度l的增大，体系基频ω1逐渐减小。另外，土体自由场位移仅对结构位移放大因子γb有显著的影响，而对结构动力放大系数ηb的影响不大；忽略土体自由场位移，当l>0.5时，结构位移放大因子γb的峰值随液化深度l的增加而减小，结构动力放大因子ηb基本保持不变，而考虑土体自由场位移，当l>0.5时，γb和ηb几乎都不随液化深度变化。

(a)当l<0.5，且us(x)=0 (b)当l>0.5，且us(x)=0

(c)当l<0.5，且us(x)≠0 (d)当l>0.5，且us(x)≠0图7 桩头动力放大因子ηp随激励频率ω的响应Fig.7 Response of the DynAFP ηp vs. exciting frequency ω

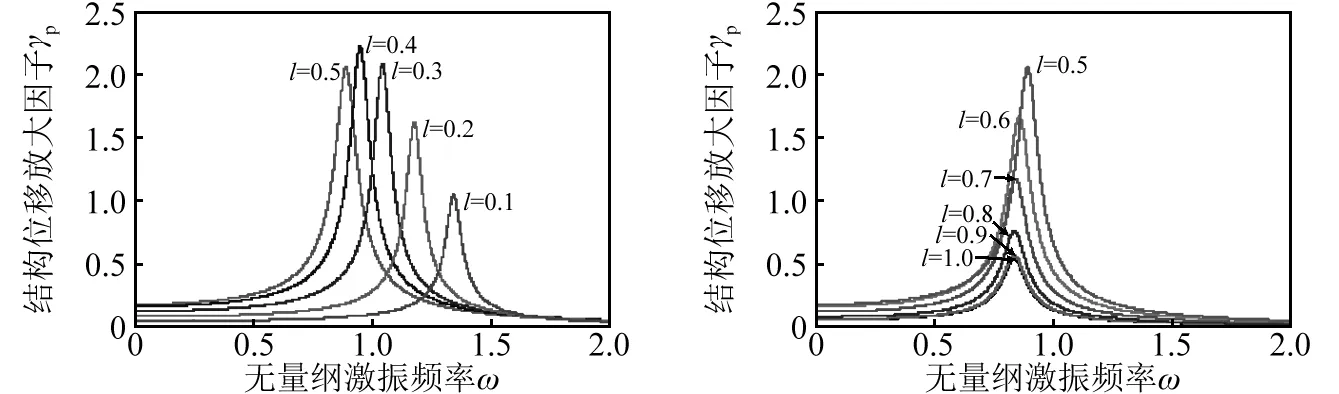
(a)当l<0.5，且us(x)=0 (b)当l>0.5，且us(x)=0

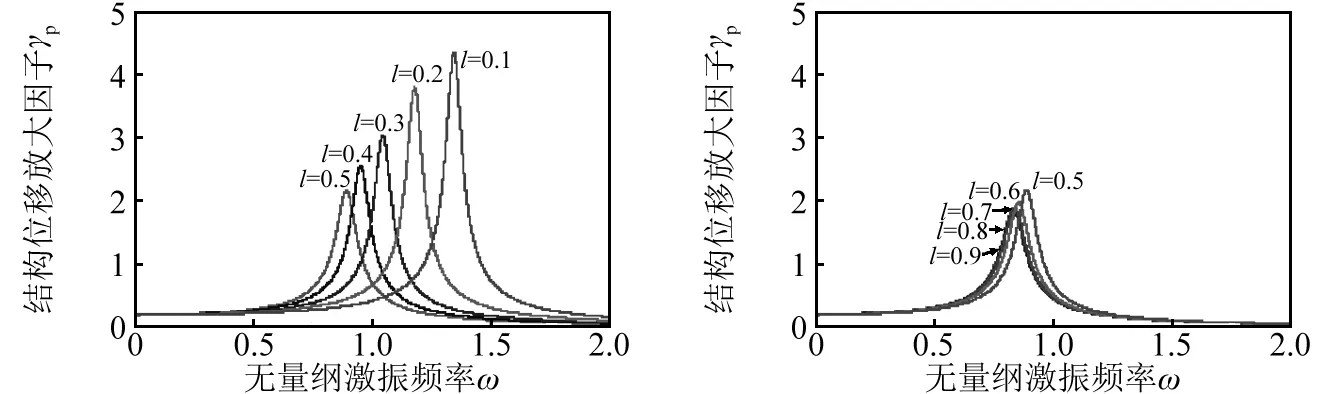
(c)当l<0.5，且us(x)≠0 (d)当l>0.5，且us(x)≠0图8 上部结构位移放大因子γb随激励频率ω的响应Fig.8 Response of the DisAFB γb vs. exciting frequency ω

(a)当l<0.5，且us(x)=0 (b)当l>0.5，且us(x)=0

(c)当l<0.5，且us(x)≠0 (d)当l>0.5，且us(x)≠0图9 上部结构动力放大因子ηb随激励频率ω的响应Fig.9 Response of the DynAFB ηb vs. exciting frequency ω

图10给出了土层液化深度l=0.4，考虑和忽略土体自由场位移时，不同上部结构侧向刚度k下桩头位移放大因子γp随无量纲激振频率ω的响应。可见，随着上部结构侧向刚度k的减小，体系基频ω1减小，而桩头位移放大因子γp峰值增大，当无量纲侧向刚度k≥30kb0时，侧向刚度k对体系基频ω1和位移放大因子γp影响较小。

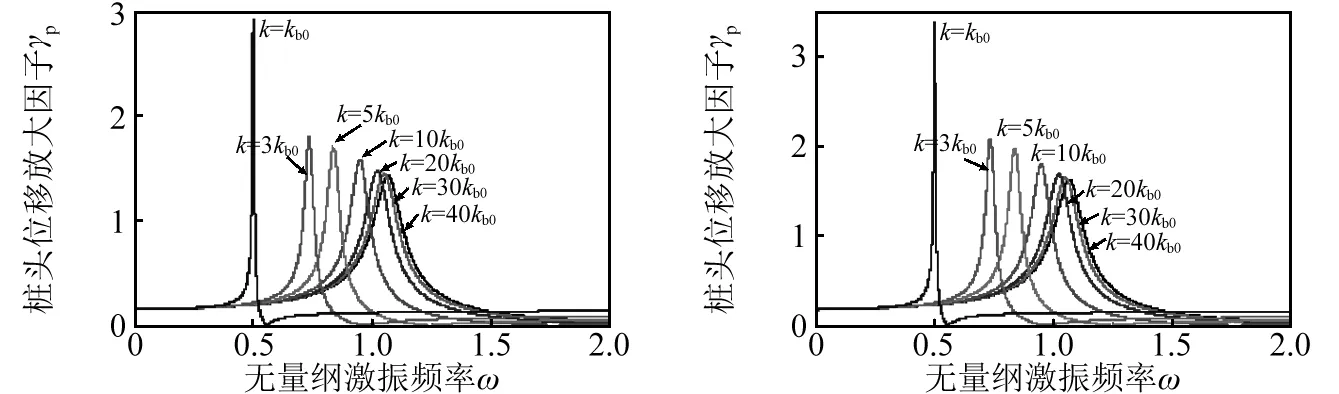
(a)当us(x)=0 (b)当us(x)≠0图10 不同侧向刚度k下的桩头位移放大因子γp随激振频率ω的响应Fig.10 Response of the DisAFP γp vs. exciting frequency ω for different lateral stiffness k

图11给出了当l=0和l=0.4，其它参数同上时，不同无量纲化轴向压力N下桩头动力放大因子ηp随无量纲激励频率ω的响应。可见，随着轴向压力N的增加，桩头动力放大因子ηp峰值和基频ω1逐渐减小。对于未液化土体(l=0)，当无量纲轴向压力N=24.91时，体系的基频ω1=0，此值即为桩失稳临界压力，即Ncr=24.91，而当土体液化深度l=0.4时，其对应的桩失稳的临界压力Ncr=8.276。同时，计算发现，桩失稳临界荷载Ncr与上部结构侧向刚度k无关。

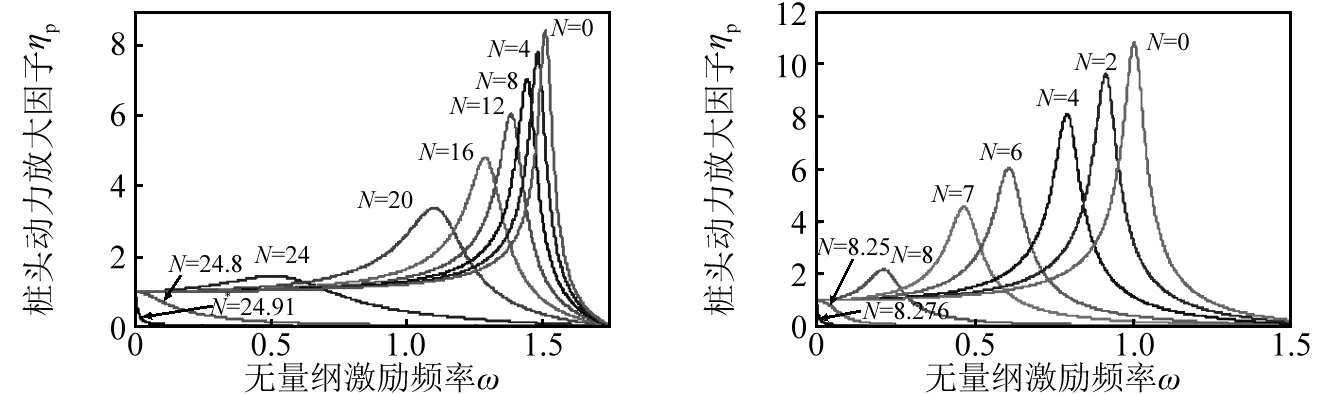
(a)未液化土体(l=0) (b)液化土体(l=0.4)图11 不同轴压N下桩头动力放大因子ηp随频率ω的响应Fig.11 Response of the DynAFP ηp vs. exciting frequency ω for different axial pressure N

图12给出了其它参数同上，不同土体液化系数βL下体系基频ω1随液化深度l的响应。可见，体系基频ω1随液化系数βL的增大而增大，当βL不变时，随着液化深度l的增加，体系基频ω1不断减小。另外，计算发现，土体未液化，即l=0时，将上部结构等效为固定于桩头质量块时的体系基频ω1=2.69，而等效为单自由度弹簧质量块时的体系基频ω1=1.47，减少约45%。可见，上部结构模型对体系基频有显著的影响。

图12 不同液化系数βL下体系基频ω1随液化深度l的响应Fig.12 Fundamental frequency ω1 of the system vs. different liquefaction depth l for different liquefaction coefficient βL

4 结 论

本文将上部结构等效为单自由度弹簧质量块，研究了桩底基岩承受垂直入射简谐SH波作用下单桩-液化土-上部结构体系的动力特性。考虑土体自由场位移，将桩等效为Timoshenko梁，基于桩-土相互作用的Winkler模型，建立了单桩-液化土-上部结构动力响应的边值问题，利用分离变量法求得了桩变形和上部结构运动的解析解。在验证理论模型和解析解正确性的基础上，分析了上部结构侧向刚度、土体液化深度和液化系数等参数对体系动力放大因子和位移放大因子的影响，并与将上部结构等效为固定于桩头质量块体系的相应结果进行比较，结果表明：

(1)将上部结构等效为单自由度弹簧质量块体系与将上部结构等效为固定于桩顶质量块体系相比，桩的失稳临界荷载相同，但弹簧质量块体系的桩头位移放大因子峰值偏大、基频偏小。

(2)土体自由场位移对桩头和结构的位移放大因子有显著影响，自由场位移将放大位移放大因子，但对结构动力放大因子影响不大。

(3)随着上部结构侧向刚度的增加，桩-液化土-上部结构体系的固有频率增大，位移放大因子峰值减小，当侧向刚度很大时，侧向刚度对体系基频和位移放大因子几乎没有影响，此时为上部结构固定于桩头的情形。

(4)随着桩轴向压力的增加，桩头动力放大因子峰值和基频逐渐减小。

(5)随着土体液化系数减小和液化深度l的增大，体系基频减小，但当液化深度超过土层厚度一半时，基频减小幅度很小。

[1] POULOS H G, DAVIS E H. Pile foundation analysis and design[M]. New York: John Wiley & Sons,1980: 336-353.

[2] 薛素铎, 刘毅, 李雄彦. 土-结构动力相互作用研究若干问题综述[J]. 世界地震工程, 2013, 29(2): 1-7.

XUE Suduo，LIU Yi，LI Xiongyan. Review of some problems about research on soil-structure dynamic interaction[J]. World Earthquake Engineering, 2013, 29(2): 1-7.

[3] 陈国兴, 金丹丹, 常向东, 等. 最近20年地震中场地液化现象的回顾与土体液化可能性的评价准则[J]. 岩土力学, 2013, 34(10): 2737-2795.

CHEN Guoxing, JIN Dandan, CHANG Xiangdong, et al. Review of soil liquefaction characteristics during major earthquakes in recent twenty years and liquefaction susceptibility criteria for soils[J]. Rock and Soil Mechanics, 2013, 34(10): 2737-2795.

[4] CHU D B, STEWART M, YOUD T L, et al. Liquefaction induced lateral spreading in near-fault regions during the1999 Chi-Chi, Taiwan earthquake[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(12): 1549-1565.

[5] YASUDA S, HARADA K, ISHIKAWA K, et al. Characteristics of liquefaction in Tokyo Bay area by the 2011 Great East Japan Earthquake [J]. Soils and Foundations, 2012, 52(5): 793-810.

[6] BHATTACHARYA S, MADABHUSHI S P G. A critical review of methods for pile design in seismically liquefiable soils[J]. Bulletin of Earthquake Engineering, 2008, 6(3): 407-446.

[7] KNAPPETT J, MADABHUSHI S. Liquefaction-induced settlement of pile groups in liquefiable and laterally spreading soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(11): 1609-1618.

[8] TANG L, MAULA B H, LING Xianzhang, et al. Numerical simulations of shake-table experiment for dynamic soil-pile-structure interaction in liquefiable soils[J]. Earthquake Engineering and Engineering Vibration, 2014, 13(1): 171-180.

[9] WAKAMATSU K, YOSHIDA N, SUZUKI N, et al. Large ground deformations and their effects on lifelines: 1964 Niigata earthquake. In case studies of liquefaction and lifelines performance during past earthquake: Japanese case studies, NCEER-92-0001[R]. New York: US National Center for Earthquake Engineering Research, 1992: 1-52.

[10] BHATTACHARYA S, HYODO M, GODA K, et al. Liquefaction of soil in the Tokyo Bay area from the 2011 Tohoku (Japan) Earthquake[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(11): 1618-1628.

[11] ABDOUN T, DOBRY R. Centrifuge scaling laws of pile response to lateral spreading[J]. International Journal of Physical Modelling in Geotechnics, 2011, 11(1): 2-22.

[12] 黄占芳, 王显耀, 吴植安, 等. 液化砂土中单桩地震响应振动台试验研究[J]. 振动与冲击, 2012, 31(20): 189-192.

HUANG Zhanfang, WANG Xianyao, WU Zhi’an, et al. Shaking table tests for single pile-soil dynamic interaction in liquefied foundations[J]. Journal of Vibration and Shock, 2012, 31(20): 189-192.

[13] CHANG B J, HUTCHINSON T C. Tracking the dynamic characteristics of a nonlinear soil-pile system in multi-layered liquefiable soils[J]. Soil Dynamics and Earthquake Engineering, 2013, 49: 89-95.

[14] BHATTACHARYA S, ADHIKARI S. Vibrational characteristics of a piled structure in liquefied soil during earthquakes: Experimental Investigation (Part I) and Analytical Modelling (Part II) [R]. Oxford University Engineering Department, Department of Engineering Science, 2007.

[15] ADHIKARI S, BHATTACHARYA S. Dynamic instability of pile-supported structures in liquefiable soils during earthquakes [J]. Shock and Vibration, 2008, 15(6): 665-685.

[16] 杨骁, 邱波. 液化土侧向扩展对具有轴向力单桩的变形影响[J]. 力学季刊, 2010, 31(1): 131-137.

YANG Xiao, QIU Bo. Influence of lateral spreading on deformation of single pile in liquefaction soils[J]. Chinese Quarterly of Mechanics, 2010, 31(1): 131-137.

[17] 杨骁, 何光辉. 成层液化土中单桩-土-结构系统的水平振动分析[J]. 上海大学学报(自然科学版), 2011, 17(6): 779-784.

YANG Xiao, HE Guanghui. Horizontal vibration analysis of pile-soil-superstructure system in layered liquefiable soil[J]. Journal of Shanghai University (Natural Science), 2011, 17(6): 779-784.

[18] 段玮玮, 黄柱, 何光辉, 等. 液化场地中Timoshenko 桩自由振动与屈曲的精确数值解[J]. 工程力学, 2013, 30(12): 138-144.

DUAN Weiwei, HUANG Zhu, HE Guanghui, et al. Exact numerical solutions for vibration and buckling of a Timoshenko pile in liquefied deposite[J]. Engineering Mechanics, 2013, 30(12): 138-144.

[19] VARUN ASSIMAKI D, SHAFIEEZADEH A. Soil-pile-structure interaction simulations in liquefiable soils via dynamic macroelements: Formulation and validation[J]. Soil Dynamics and Earthquake Engineering, 2013, 47(Sup1):92-107.

[20] NI S H, XIAO X, YANG Y Z. A p-y curve-based approach to analyze pile behavior in liquefied sand under different stress states[J]. Journal of Geoengineering, 2014, 9(3): 85-93.

[21] MOKHTAR A S A, ABDEL-MOTAAL M A, WAHIDY M M. Lateral displacement and pile instability due to soil liquefaction using numerical model[J]. Ain Shams Engineering Journal, 2014, 5(4):1019-1032.

[22] TANG L, MAULA B H, LING X Z, et al. Numerical simulations of shake-table experiment for dynamic soil-pile-structure interaction in liquefiable soils [J]. Earthquake Engineering and Engineering Vibration, 2014, 13(1): 171-180.

[23] MISKO C, KENJI I. Simplified method for analysis of piles undergoing lateral spreading in liquefied soils [J]. Soils and foundations, 2004, 44(5): 119-133.

[24] KOO K K, CHAU K, YANG X, et al. Soil-pile-structure interactions under SH waves [J]. Earthquake Engineering and Structural Dynamics, 2003, 32(3): 395-415.

[25] HAN S M, BENAROYA H, WEI T. Dynamic of transeversely vibrating beams using four engineering theories [J]. Journal of Sound and Vibration, 1999, 225(5): 935-988.

[26] TOKIMATSU K, ASAKA Y. Effects of liquefaction-induced ground displacements on pile performance in the 1995 Hyogeken-Nambu earthquake [J]. Soils and Foundations, 1998, Special Issue (2): 163-177.

[27] BHATTACHARYA S, MADABHUSHI S P G, BOLTON M D. An alternative mechanism of pile failure in liquefiable deposits during earthquakes [J]. Geotechnique, 2004, 54(3): 203-213.

[28] BHATTACHARYA S, ADHIKARI S, ALEXANDER N A. A simplified method for unified buckling and free vibration analysis of pile-supported structures in seismically liquefiable soils [J]. Soil Dynamics and Earthquake Engineering, 2009, 29(8): 1220-1235.

[29] 林基聪. 液化场地桥梁群桩基础抗震简化分析方法[D]. 哈尔滨: 哈尔滨工业大学, 2012.

Horizontalvibrationcharacteristicsofapile-liquefiedsoil-superstructureunderSHwave

SHAO Yanli, FANG Xiaowen, YANG Xiao

(Department of Civil Engineering，Shanghai University，Shanghai 200072，China)

Treating a pile and a superstructure as a Timoshenko beam and a single degree of freedom spring-mass system, respectively, the horizontal vibration characteristics of the pile-liquefied soil-superstructure coupled system subjected to a vertical incident harmonic SH wave was investigated based on the Winkler model of the pile-soil interaction. The boundary value problem of the single pile-liquefied soil-superstructure coupled system was established, in which the free-field displacement of the soil, translational and rotational inertia of the superstructure and the second order effect of the axial pressure of the pile were taken into consideration. And the analytical solutions of the pile deformation and superstructure motion were derived. The influences of the geometry and physics parameters on the displacement amplification factors and dynamic amplification factors at the pile top and of superstructure were examined numerically. It is shown that there exists an evident resonance phenomenon in the single pile-liquefied soil-superstructure system, and the influence of the soil free-field displacement on the displacement amplification factors of the pile top and superstructure is remarkable. Furthermore, with the increase of the superstructure stiffness, fundamental frequency of the single pile-liquefied soil-superstructure system increases and the peak value of displacement amplification factors decreases. At the same time, with the development of soil liquefaction degree, the fundamental frequency and dynamic amplification factors of the single pile-liquefied soil-superstructure system decreases.

SH wave; liquefied soil; pile-soil-structure interaction; Winkler model; dynamic characteristics; analytical solution

国家自然科学基金项目(10872124)

2016-04-27 修改稿收到日期： 2016-07-18

邵艳丽 女，硕士生，1990年生

杨骁 男，博士，教授，1965年生

TU473.1

A

10.13465/j.cnki.jvs.2017.20.032