铝板--环氧树脂夹层结构本构模型研究

谢永亮 赵 亮 贾广发

（空军勤务学院机场工程与保障系， 江苏 徐州 221000）

铝板
--环氧树脂夹层结构本构模型研究

谢永亮 赵 亮 贾广发

（空军勤务学院机场工程与保障系， 江苏 徐州 221000）

运用大型有限元软件 ANSYS/LS-DYNA，在相同的爆炸冲击波作用下，对掩蔽物上方含环氧树脂夹层铝板防护结构的抗爆性能进行了数值模拟，通过模拟结果，建立不同环氧树脂夹层厚度的复合结构的本构模型，为防护结构的工程实践提供了一定的参考。

环氧树脂夹层；抗爆性能；数值模拟；本构方程

0 引言

现代战争，精确制导武器获得大规模使用，发现即意味着摧毁，因此在提高隐蔽性的同时，也要加强防护目标结构的强度。目前新型防护材料研究较多，其中铝板材料所具备的质量轻、强度高、刚性好、环氧树脂质量轻，缓冲吸能性能好等优点表现较为出色[1]。本文通过采用大型模拟软件 ANSYS/LS-DYNA对不同环氧树脂夹层厚度的复合板结构进行模拟，探讨出环氧树脂以及其厚度对冲击波的衰减作用，得出新型复合材料的在爆炸冲击波作用下的本构模型，为工程防护提供一定的参考。

1 试验设计

试验实体的物理尺寸为：掩蔽物尺寸为24cm×4 cm×4cm，炸药为2 cm×4 cm×1 cm，上下层铝板为24cm×4cm×1cm，环氧树脂夹层的的尺寸为24cm×4cm×0.5cm、24cm×4cm×1cm和24cm×4cm×2cm，为了节省程序运算时间，考虑模型的对称性，建立1/4模型进行简化运算。另外为对比研究环氧树脂厚度变化对试验结果的影响，设炸药从上表面起爆，控制起爆点到掩蔽物上表面，即下层铝板的下表面的距离不变为7cm。本试验控制上下层铝板厚度为1cm不变，变量为中间夹层环氧树脂厚度，分别为0.5、1、2cm，试验编号分别为A,B,C，如表1所示：

表1 A,B,C号试件参数

2 数值模拟

2.1 材料状态方程与模型

数值模拟所采用的材料主要为TNT炸药、空气、铝板、环氧树脂。

数值模拟所采用的 TNT炸药选用材料类型 8，密度为 1.63g/cm3，爆速为0.693cm/μs，CJ压力为21Gpa，采用JWL状态方程，此状态方程通常用于描述高能炸药及爆轰产物[2]，其形式为：

其中，A，B，R，R’，错误！未找到引用源。是材料常数，P是压力，V是相对体积，E是初始内能。分别取A=373.8Gpa，B=3.747 Gpa，R=4.15，R’=0.9，错误！未找到引用源。=0.35，E=9.6GJ/m3。

空气采用下面的气体状态方程来模拟，该状态方程为：

P=（γ-1）ρE

其中，P是压力，γ是气体热指数，ρ是相对密度，E是空气内能。分别取γ=1.4，ρ=1.3×10-3g/ cm3，E=2.5×10-6（105MPa）。

铝板采用DYNA Johnson-Cook本构模型进行模拟，材料参数分别为：ρ=2.7g/cm3，E=72Gpa，σ=0.33。

环氧树脂的应力应变关系采用LS-DYAN中的ELASTIC_PLASTIC_HYDRO本构模型，其参数值分别为：ρ=0.980 g/ cm3，弹性模量1Gpa，泊松比为0.38。

数值模拟过程中，炸药、空气、铝板和环氧树脂均采用3D SOLID164单元类型，炸药和空气使用欧拉算法，铝板和环氧树脂采用拉格朗日算法，炸药和空气单元不存在畸变问题，铝板环氧树脂夹层结构与炸药和空气采用耦合算法，计算时在对称面方向上进行面约束位移，在 Z方向即厚度方向上进行节点约束位移，数值模拟采用cm-g-μs单位制。

2.2 数值模拟结果分析

为考虑爆炸对结构的最大影响，选取炸药正下方处、下层铝板背面的单元进行分析，主要分析其在冲击波作用下σ-ε(应力-应变)关系，如图 1所

图1 复合材料的动态缓冲性能影响因素分析 图2 形状函数的数据拟合曲线

从图中可以看出：随着环氧树脂夹层厚度的增加，对于发生相同应变的结构，3组试件的下层铝板处所测应力呈现先减小后增大的趋势。曲线反映出：对于发生相同应变的情况下，B组试件中下层铝板内发生的应力达到最小，说明中间缓冲层吸能效果最好。

3 本构方程的构建

本构方程在所得应力-应变关系曲线的基础上，决定采用张勇[3]等在SHERWOOD J A等提出的经验型本构关系：σ=H(T)G(ρ)M(ε, ε’)f(ε)基础上所提出的σ=[A(ρ-ρ0)+1]

[B(V-V0)+1]错误！未找到引用源。εi的形式，选取 A组试件作为参考，对形状函数f(ε)用多项式进行描述，经过origin线性拟合，得到相关参数见表2，f(ε)数据拟合求解图如图2所示。

表2 A试件拟合参数

图3 形状函数拟合后的残差检验图 图4 环氧树脂厚度拟合曲线

由此可知拟合得到的形状函数为：f(ε)= 185.11ε6-293.17ε5+142.05ε4-6.64 ε3-12.32ε2+3ε-0.01。

本次拟合的残差图见图3，残差表示变量与拟合曲线纵坐标之间符合拟合函数的显著程度，从图中可以看出，拟合效果较好，R2为0.00962。

利用得到的形状函数进一步确定本构方程的表达式，结合 B,C两组试件的应力应变曲线发现：相同的应变情况下，应力呈现先减小后增大的趋势，考虑采用二次函数来对这一情况进行拟合，拟合结果如图 4所示。从图中可以看出，三个点均落在该二次函数曲线上，说明二次函数描述不同环氧树脂厚度对试验结果的影响效果是可以的，该曲线的表达式为：

Y=0.965h2-2.75h+2.13，其中h为中间夹层环氧树脂的厚度，单位为厘米。

因此，对于上下夹层为1cm厚铝板，中间夹层为环氧树脂复合防护结构的本构方程表示为：σ=（0.965h2-2.75h+2.13）（185.11ε6-293.17ε5+142.05ε4-6.64 ε3-12.32ε2+3ε-0.01）。

通过推导出的本构关系对其余试件进行应用，达到本构模型验证的目的，结果发现所得本构模型对试件的拟合有一定的效果，曲线大部分能够包括实际数值点，如图5所示：

总的看来，本构方程拟合得到的曲线对于复合结构在爆炸冲击波作用下的响应拟合较好，能够基本上反映出复合结构在爆炸冲击波作用下的动态动力响应过程，另外，本构方程对于各个试件对应的各应变区间把握的不错，基本保持了与试件各阶段对应应变区间的同步化，所得结果为工程实践提供了一定的参考。

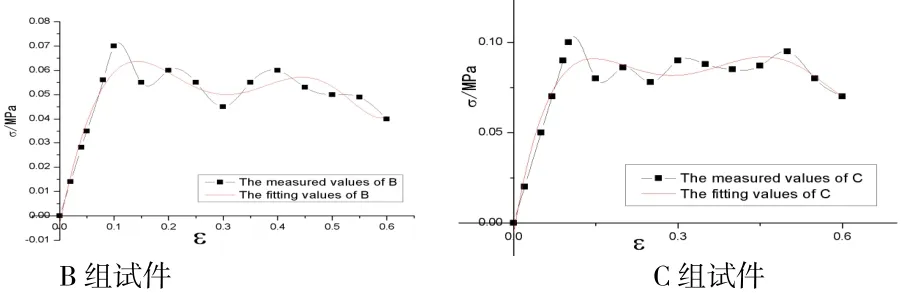
图5 其余试件的本构模型曲线与实际数据曲线的对比

4 结语

（1）环氧树脂夹层能够对冲击波起到一定的缓冲作用，但缓冲效果并不随着厚度的增加而线性增加。综合看来，当环氧树脂夹层厚度为1cm，即复合板由1cm厚上层铝板、1cm厚环氧树脂中间夹层和1cm厚下层铝板组合时整体缓冲效果最好。

（2）对于上下夹层为1cm厚铝板，中间夹层为环氧树脂复合防护结构的本构方程表示为：σ=（0.965h2-2.75h+2.13）（185.11ε6-293.17ε5+142.05ε4-6.64ε3-12.32ε2+3ε-0.01）。

[1]杜修力.炸药爆炸作用下地下结构的动力响应分析[J].爆炸与冲击，2006，26（5）：13-20

[2]边小华，石少卿，康建功等.一种新型防护结构对爆炸冲击波衰减特性的研究[J].后勤工程学报，2005：40-45

[3]张勇等.聚氨酯蜂窝纸板动力学性能及其本构模型[J].材料工程，2015，43（5）：27-32

TU512.4

A

1007-6344（2017）09-0287-02

谢永亮，中国人民解放军空军勤务学院机场工程与保障系，教授

赵亮， 中国人民解放军空军勤务学院机场工程与保障系，硕士研究生，江苏省徐州市西阁街85号一大队一队 221000