关于广义几何数列的讨论
张立国
(沈阳理工大学 理学院,沈阳 110159)
关于广义几何数列的讨论
张立国
(沈阳理工大学 理学院,沈阳 110159)
广义几何数列是数列的推广,其收敛情况与数列的值域密切相关。按照数列的取值范围,讨论广义几何数列的性质,给出收敛的充要条件和必要条件,为极限理论的后续研究提供思路。
广义几何数列;倒数代换;收敛
数列极限是微积分学中最简单、最容易掌握的极限概念。虽然它不具有广泛的代表性,但由于分析学中的极限大多可以利用数列极限来刻划,因而它的地位是不言而喻的。广义几何数列是数列概念的推广,其性质对于极限理论的完善和发展是非常重要的。文献[1]只在区间[0,1]上对其进行简单的讨论,但对于区间[0,1]以外的广义几何数列没有涉及。本文在此基础上,系统地讨论广义几何数列的收敛情况,并给出收敛的充要条件。
1 预备知识
定义1[1]设{xn}为数列,令
称数列{an}为广义几何数列。{xn}为{an}的基础数列。
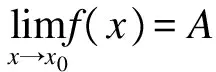
2 广义几何数列的收敛条件
如果基础数列x1=x2=…=xn=…=r,则an=rn,此时这个广义几何数列{an}就是通常的几何数列{rn},因而在区间[0,1]之内,广义几何数列与几何数列有相似的性质。
命题1[1]设基础数列{xn}(0,1),则广义几何数列{an}收敛 。
命题2 设基础数列{xn}(-1,0),若广义几何数列{an}收敛于a,则a=0。
证明由于基础数列{xn}(-1,0),则a2n(0,1),a2n-1(-1,0)。据极限保号性可知由于广义几何数列{an}收敛a,从而故a=0。
若基础数列{xn}位于区间[0,1]之外时,广义几何数列{an}收敛情况如下:
定理2 设基础数列{xn}(-∞,-1),则广义几何数列{an}发散。
证明由于基础数列{xn}(-∞,-1),则a2n(1,+∞),a2n-1(-∞,-1)。若与都存在时,据极限保号性可知从而因此广义几何数列{an}发散。

定理3 设xn(1,+∞),则广义几何数列{an}收敛当且仅当级数收敛。
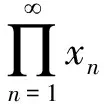
由拉格朗日(Lagrange)中值定理得
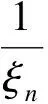
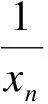
由归结原则与洛必达法则有
根据数项级数收敛的必要条件,可以得出广义几何数列收敛的必要条件:
推论1 设xn(1,+∞),若基础数列{xn}的广义几何数列{an}收敛,则数列{xn}收敛于1。
利用倒数代换和逆否命题,可以得到xn(0,1)时,广义几何数列{an}收敛结论。
定理4[3]设xn(0,1),则广义几何数列{an}的极限大于0,当且仅当级数收敛。
定理5 设xn(0,1),则广义几何数列{an}的极限为0,当且仅当级数发散。
推论2 设xn(0,1),若数列{xn}的广义几何数列{an}极限大于0,则数列{xn}收敛于1。
合并推论1与2可以得到推论3。
推论3 设xn(0,+∞),若数列{xn}的广义几何数列{an}极限大于0,则数列{xn}收敛于1。
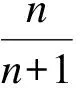

例1说明推论2只是必要条件。通过倒数代换可以推知,推论1与推论3也仅是必要条件。
3 广义几何数列的性质
定理6 若实数a(0,+∞),则存在收敛于1的基础数列{xn},使得其广义几何数列收敛于a。
证明设基础数列{yn|nN}={0.9,0.99,0.999,…,1-(0.1)n,…},其广义几何数列{bn}的极限为p,即据极限保号性可知0 (1)若0 当r>a时,由(1)可知,存在xn(0,1),且使得广义几何数列{an}收敛于a; 当r=a时,xn=zn使得结论成立。 (4)若a=1或p时,令xn1或yn,即为所求。 由定理6的证明过程可以得到如下结论。 定理7 若实数a(0,1),则存在收敛于1的基础数列{xn}(0,1),使得其广义几何数列{an}收敛于a。 定理8 若实数a[1,+∞),则存在收敛于1的基础数列{xn}(1,+∞),使得其广义几何数列{an}收敛于a。 由例1与定理6的证明可以看出,广义几何数列{an}的极限值a的大小与数列{xn}收敛于1的速度有关,当{xn}缓慢的收敛于1时,a可能为0,而当{xn}快速的收敛于1时,a可能大于0,这个问题需要深入探讨。 通过本文的论证可以看到,广义几何数列的收敛不仅与基础数列的值域有关,而且与数项级数的收敛联系密切。若把两者有机地联系在一起时,可能得到判定数项级数收敛的新方法,这是下一步研究的重点。 [1] 邱森.微积分探究性课题精编[M].武汉:武汉大学出版社,2016. [2] 华东师范大学数学系.数学分析[M].北京:高等教育出版社,1980. [3] Ahlfors L.Complex analysis [M].3rd ed.Mcgraw-Hill,New York,1979. (责任编辑:马金发) TheConvergenceofGeneralizedGeometricSequence ZHANG Liguo (Shenyang Ligong University,Shenyang 110159,China) The generalized geometric sequence is a generalization of the sequence,the convergence of the situation and the range of values of the sequence are closely related.According to the sequence of the scope,to discuss the nature of the generalized geometric sequence,and to present the necessary and sufficient conditions and necessary conditions of the convergence,and to provide ideas for the subsequent research in the theory of limit. generalized geometric sequence;inverse substitution;convergence O13 A 2016-10-26 张立国(1970—),男,副教授,研究方向:模糊拓朴学。 1003-1251(2017)05-0108-03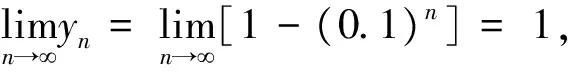
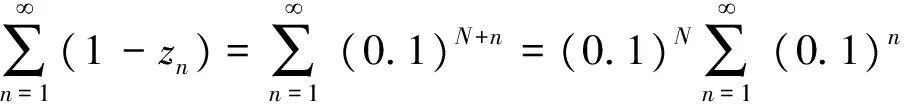
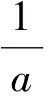
4 结束语

