抗磁悬浮能量采集器振动与输出特性分析*

张振宇,苏宇锋,秦立振

(郑州大学机械工程学院,郑州 450001)

项目来源:国家自然科学基金(51475436);河南省重点科技攻关(152102210042)

2017-03-23修改日期2017-05-22

抗磁悬浮能量采集器振动与输出特性分析*

张振宇,苏宇锋*,秦立振

(郑州大学机械工程学院,郑州 450001)

对抗磁悬浮振动能量采集器中悬浮永磁体的非线性振动特性进行了分析,并在此基础上分析了感应线圈结构参数对输出特性的影响。利用MATLAB软件的Simulink组件仿真分析采集器的非线性振动特性,利用有限元分析软件COMSOL对能量采集器的输出特性进行了仿真分析。通过改变线圈参数发现,在线圈体积一定时,输出功率变化很小,电压随着铜线直径减小增加很快,所以可以通过微细加工减小铜线直径的方法来提高线圈的输出电压。最终在线圈总体积约为6.4 mm3,铜线直径为0.02 mm,匝数为500匝时,得到的电压峰值达到约93.8 mV。

振动能量采集器;振动及输出特性;仿真分析;结构参数优化

随着技术的发展和进步无线传感器网络在现代诸多领域得到了广泛地应用,其主要通过电池供电[1-2]。由于电池能量有限,当电量耗尽时必须更换电池,传感器网络才能正常工作,而对于不便于更换电池的场所,传统电池显现了其固有的局限性。利用环境中存在的能量为各种元器件供电是代替传统化学电池的有效手段之一。其中振动能量便是空间中广泛存在的能量形式之一,振动能量采集器能把环境中的振动能量转换为电能为电子元器件供电。

目前各国研究人员已经提出了很多种振动能量采集器[3],包括压电式、静电式和电磁式等[4]。其中抗磁悬浮振动能量采集器由于其低频率低阻尼的特性得到了越来越多的关注。抗磁悬浮最早由Werner Braunbek提出,最近几年抗磁悬浮技术得到了深入的研究[5]。西北工业大学的Qian A R等人[6]利用抗磁悬浮研究微重力环境下生理变化的分子机制。他们通过利用抗磁悬浮在地表创建微重力环境,使得实验变得简单、成本低廉,并且取得了良好的效果。美国伦斯勒理工大学的Anton Tkachenko等人[7]提出基于抗磁悬浮的小型电子元件的定向组装方法。得益于抗磁悬浮状态下的低摩擦可以实现在微作用力下的快速精准的定向组装。法国弗朗什-孔泰大学的Margot Billot等人[8]提出的基于抗磁悬浮的纳米力传感器,实现了高分辨,强抗干扰和无源自动补偿。奥地利约翰开普勒林茨大学的Stefan Clara等人[9]提出的基于抗磁悬浮的粘度和密度传感器,具有高灵敏度,测量室无机械和电气连接的优点;Wolfgang Hilber等人[10]提出的磁驱动薄膜执行机构,可以在无外部能量输入的情况下调整中性膜的位置,驱动和执行机构的分离也扩大了设备的应用范围。抗磁悬浮利用的磁力弹簧具有低刚度系数,低阻尼,长寿命的优点[11]。利用磁力弹簧代替普通物理弹簧已经在振动能量采集器中得到广泛地利用。美国北卡罗纳州立大学的Palagummia S等人提出的基于垂直和水平抗磁悬浮振动能量采集器[12-13]输出功率分别达到了1.72 μW和3.6 μW,垂直结构运用了提升和举起磁体增大了在竖直方向的悬浮空间,但是同时导致水平抗干扰能力的下降,水平结构利用两块提升磁体扩大了悬浮空间提升了垂直稳定性,但是同时导致整体结构增大。郑州大学的苏宇锋等人[14-15]提出了一种新型的抗磁悬浮振动能量采集器并对其进行了理论分析和仿真研究,本文在此基础上对抗磁悬浮振动能量采集器的非线性力以及非线性振动进一步分析,并分析了线圈结构参数对采集器输出特性的影响。

图1 抗磁悬浮振动能量采集器的模型

1 悬浮永磁体振动分析

抗磁悬浮振动能量采集器是由提升永磁体、悬浮永磁体、高定向热解石墨(HOPG)板以及铜线圈组成,结构模型如图1所示。其中悬浮永磁体(N42)剩磁为1.3 T,尺寸直径×高度为3.2 mm×1.6 mm,提升永磁体(N52)剩磁为1.45 T,尺寸直径×高度为4.8 mm×3.2 mm,上、下高定向热解石墨板为完全相同的两个圆柱,直径×高度为10 mm×1.5 mm,磁化率χm为(-8,-8,-45)×10-5。提升磁体与悬浮磁体之间的吸引力可以克服悬浮磁体所受到的部分重力,并且限制悬浮磁体水平方向的运动。由于吸引力随着悬浮磁体的位置变动而发生变化所以竖直方向并不能稳定悬浮。通过增加高定向热解石墨板引入抗磁力限制悬浮磁体在竖直方向的运动,实现了悬浮磁体的稳定悬浮。当受到外界振动激励时,平衡被破坏,悬浮永磁体相对线圈运动,使得线圈内的磁通量发生变化进而在线圈内产生感应电压。

由于抗磁力相对于磁力、重力十分微弱,且有效作用距离只有毫米量级,所以高定向热解石墨板间距是影响悬浮磁体振动特性的最主要参数之一。当高定向热解石墨板间距较小时,抗磁力表现为良好的线性特性,当间距不断增大时,非线性特性逐渐增强。

采用COMSOL有限元仿真软件计算永磁体,以及高定向热解石墨板之间的作用力。图2是高定向热解石墨板处于不同间距时的抗磁力随悬浮磁体位置的变化曲线。由于同时受到高定向热解石墨板物理边界、抗磁力边界的双重影响,悬浮磁体会分别出现1个、2个、3个平衡点。只出现一个平衡点时,此点即为稳定平衡点,悬浮磁体可以在外界激励下达到最大振动位移。当有3个平衡点时,中间点为非稳定平衡点,上下两个点为稳定平衡点,此时悬浮磁体的初始位置和外界激励会影响悬浮磁体的振动状态。当有两个平衡点时,中间点为不稳定平衡点,负平衡点为稳定平衡点,但是此时悬浮磁体受到外界干扰时很可能跳到正极限点而无法完成持续振动。

图2 磁力-重力、抗磁力曲线

由于单平衡点的振动范围过小,不利于振动能量采集器输出性能的提高,所以需要悬浮磁体产生双平衡点振动。双稳态运动可以提高能量采集器的采集效率和频率带宽,并且能在低频率、小幅值激励下产生大幅值周期运动[16],达到改善其输出性能的目的[17]。在MATLAB的Simulink模块中建立如图3(a)所示的模型分析系统的振动响应。如图3(b)是高定向热解石墨板间距为4 mm,初始位置在正平衡点时不同输入状态下悬浮磁体的振动特性。当输入振幅为2 mm时,悬浮磁体仅能在正平衡点附近振动;当输入振幅达到3.9 mm时,悬浮磁体能够获得较大的振动位移。

图3 悬浮磁体振动响应的Simulink模型 和悬浮磁体振动输出

图4 永磁体上方1 mm处BZ随高度变化

2 输出特性分析

线圈所在空间的磁场梯度、线圈的结构参数等是影响线圈感应电动势的主要因素。在COMSOL中建立悬浮磁体在空气域中相对于线圈的运动模型,分析不同时刻线圈所在平面内磁感应强度的变化。

图5是紧密缠绕的单层平面螺旋线圈,在线圈内半径ri为零,线圈外半径ro不断增大的情况下,感应电动势的变化曲线。可看出感应电动势的变化和磁体振动保持一致,表现出周期变化规律,且随着线圈外半径ro的增加而增大。

图5 电动势随线圈外径的变化

图6是感应电动势的峰值和电阻随线圈外半径ro的变化曲线。由图6可以看出当线圈外半径ro较小时,感应电动势随线圈外半径ro增加并不明显,当ro较大时电压增量趋于稳定值,在中间一定范围内受线圈外半径ro增加的影响较大。所以去掉平面螺旋线圈中心的几匝铜线对电压的输出峰值影响不大。

图6 峰值电压和电阻随线圈外径的变化

图7是线圈输出功率的峰值随着线圈外半径ro的变化趋势。由图7可以看出当线圈外半径ro较小时功率的增量极小,输出的功率接近零。当线圈外半径ro继续增加时输出的功率峰值迅速增加,当达到某一值时,功率出现极值,然后开始下降。结合图6中的电压和电阻曲线可以选定线圈的最佳内半径ri和最佳外半径ro,分别为2.6 mm和7.6 mm。同时,在线圈输出功率的峰值取得最大值时,可以适当增加或减小线圈半径以调节电压而不会造成输出功率的大幅衰减。

图7 功率峰值随线圈外径的变化

绕制平面螺旋线圈所用铜线的直径会影响线圈的总电阻和线圈的厚度。图8是感应线圈电动势和功率的峰值随铜线直径的变化曲线。由图8可以看出当线圈内外径保持不变时,所用铜线直径越小电压峰值增加越快,输出功率衰减梯度近似为固定值,但电阻急剧增大。随着铜线直径的减小,感应线圈的厚度也在减小,所以可以通过增加线圈的层数来提高整体输出电压。同时也可以通过选择不同直径的铜线调节采集器的等效输出阻抗。

图8 电压峰值、功率峰值随铜线直径的变化

图9 电参量总和

采集器的体积是制约线圈参数的另一主要因素,当线圈所允许排布的空间为某一定值时,铜线的直径就能与线圈的总层数建立直接的关系。图9是在线圈总体积不变得情况下得到的电压、功率相对于铜线直径的变化规律。由图9可以看出在线圈体积不变时,总的输出功率随着绕制铜线直径的变化仅仅表现出轻微的变化,可以认为单位体积线圈所能采集的功率固定不变。

由于受悬浮空间的限制,线圈层数不能太多,结合线圈的输出特性以及悬浮磁体的悬浮空间选定线圈层数为2层。如图10是线圈层数为2层,匝数为500匝,内外径分别为2.6 mm和7.6 mm时得到的电压和功率随时间的变化曲线。由图10可以看出采集器输出电压峰值达到约93.8 mV,功率峰值达到约2.74 μW。

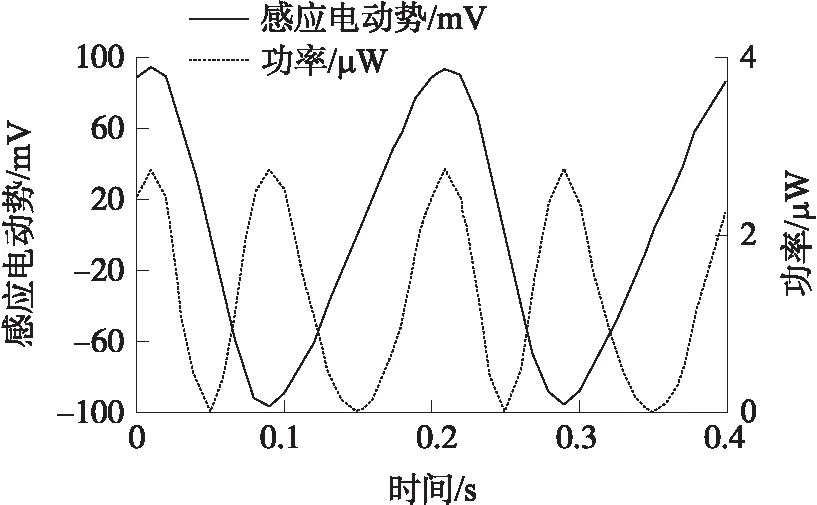
图10 电动势和功率曲线

3 结论

本文通过对抗磁悬浮振动能量采集器受力分析,得到了悬浮磁体在不同初始位置不同输入条件下的振动曲线。通过COMSOL仿真分析并结合MATLAB确定了线圈的最佳位置和大小。发现在结构尺寸选定后,选用不同直径铜线绕制的线圈总输出功率几乎不变。通过选用直径更大或者更小的铜线绕制线圈可以单独调节采集器的输出电压,使得输出电压增加或者减小。综合各种因素最终选定模型的线圈总体积为约6.4 mm3,铜线直径为0.02 mm时,层数为2层。最终得到的电压峰值达到约93.8 mV,功率峰值达到约2.74 μW。

[1] 张希伟,戴海鹏,徐力杰,等. 无线传感器网络中移动协助的数据收集策略[J]. 软件学报,2013,24(2):198-214.

[2] 司海飞,杨忠,王珺. 无线传感器网络研究现状与应用[J]. 机电工程,2011,28(1):16-20.

[3] Lei Liu,Yuan F G. Diamagnetic Levitation for Nonlinear Vibration Energy Harvesting:Theoretical Modeling and Analysis[J]. Sound and Vibration,2013,332(2):455-464.

[4] 许卓,杨杰,燕乐,等. 微型振动式能量采集器研究进展[J]. 传感器与微系统,2015,34(2):9-13.

[5] 李世鹏,张卫平,陈文元,等. 抗磁悬浮的原理、特点和应用[J]. 磁性材料及器件,2011,42(1):1-6.

[6] Qian A R,Yin D C,Yang P F,et al. Application of Diamagnetic Levitation Technology in Biological Sciences Research[J]. IEEE Transactions on Applied Superconductivity,2013,23(1):54-59.

[7] Anton Tkachenko,James J Q Lu. Directed Self-Assembly of Mesoscopic Electronic Components into Sparse Arrays with Controlled Orientation Using Diamagnetic Levitation[J]. Journal of Magnetism and Magnetic Materials,2015,385:286-291.

[8] Margot B,Emmanuel P,Jo⊇l A,et al. External Mechanical Disturbances Compensation with a Passive Differential Measurement Principle in Nanoforce Sensing Using Diamagnetic Levitation[J]. Sensors and Actuators A:Physical,2016,238:266-275.

[9] Clara S,Antlinger H,Abdallah A,et al. An Advanced Viscosity and Density Sensor Based on Diamagnetically Stabilized Levitation[J]. Sensors and Actuators A:Physical,2016,248:46-53.

[10] Wolfgang H,Bernhard J. A Magnetic Membrane Actuator in Composite Technology Utilizing Diamagnetic Levitation[J]. IEEE Sensors Journal,2013,13(7):2786-2791.

[11] Giorgio De Pasquale,Sonia Iamoni,Aurelio Soma. 3D Numerical Modeling and Experimental Validation of Diamagnetic Levitating Suspension in the Static Field[J]. International Journal of Mechanical Sciences,2013,68:56-65.

[12] Palagummia S,Yuan F G. An Optimal Design of a Monostable Vertical Diamagnetic Levitation Based Electromagnetic Vibration Energy Harvester[J]. Sound and Vibration,2015,342:330-345.

[13] Palagummia S,Zhou J,Yuan F G. A Horizontal Diamagnetic Levitation Based Low Frequency Vibration Energy Harvester[J]. Vibration and Acoustics,2015,137(6):061004-10.

[14] Zhitong Ye,Zhiyong Duan,Kenichi Takahata,et al. Motion Characteristics and Output Voltage Analysis of Micro-Vibration Energy Harvester Based on Diamagnetic Levitation[J]. Appl Phys A,2015,118(1):91-100.

[15] 秦立振,苏宇锋,刘武发. 抗磁悬浮能量采集器结构参数对输出特性的影响[J]. 电子测量与仪器学报,2016,30(9):1438-1443.

[16] 王光庆,张伟,刘创. 非线性压电振动能量采集器的振动特性与实验研究[J]. 传感技术学报,2015,28(10):1494-1502.

[17] 杨斌强,徐文潭,王学保,等. 带弹性放大器的双稳态压电振动能量采集器[J]. 传感技术学报,2017,30(5):684-691.

OutputCharacteristicandVibrationCharacteristicAnalysisofMicro-VibrationEnergyHarvesterBasedonDiamagneticLevitation*

ZHANGZhenyu,SUYufeng*,QINLizhen

(School of Mechanical Engineering,Zhengzhou University,Zhengzhou 450001,China)

On the basis of analyzing the nonlinear vibration characteristics of levitation permanent magnet in the diamagnetic vibration energy harvester,we could analyze the infuences of structure parameters to the output characteristics of the induction coil. We used MATLAB to simulate nonlinear vibration characteristics of micro-vibration energy harvester and the finite element analysis software COMSOL to simulate the output characteristics of energy harvester. By changing the coil parameters,we found that when the coil volume was determined,the changes of output power were very small but the voltage increased quickly with the increasing of coil diameter. Therefore,the output voltage of the coil could be improved by reducing the diameter of the wire by micro machines. Finally,when the total volume of the coil was about 6.4 mm3,wire diameter was 0.02 mm,coil number were 500,the voltage-peak reached about 93.8 mV.

vibration energy harvester;vibration and output characteristic;simulation analysis;optimum of structure param

TH703

A

1004-1699(2017)10-1488-05

10.3969/j.issn.1004-1699.2017.10.006

张振宇(1989-),2015年于沈阳工业大学获得学士学位,主要研究方向为微型能量采集器,1373683949@qq.com;

苏宇锋(1977-),博士,郑州大学机械工程学院教授,主要研究方向为微型振动能量采集器与微型驱动器,yufengsu@zzu.edu.cn。