随机振动信号的小波去噪分析

曹建华，杨超

(黄山学院机电工程学院，安徽黄山245041）

随机振动信号的小波去噪分析

曹建华，杨超

(黄山学院机电工程学院，安徽黄山245041）

振动在生活生产中十分常见，对振动信号分析处理是机械装备故障诊断的重要手段。但采集到的信号往往混杂着各种噪音，如何消噪用何种方式消噪直接关系下一步的诊断分析。利用小波分析法尝试对信号进行了不同方式去噪处理，最后采用Welch法估计功率谱密度曲线，并与未做消噪处理生成的PSD曲线进行对比，小波去噪之后的信号生成的功率谱密度更能清晰地显示各个频率上振动能量，方便工程设计和诊断机械装备故障所在。

数字信号；振动；MATLAB；小波分析

1 前言

小波在信号处理方面有着广泛的应用。人类历史上第一个小波变换最早是在1909年由Alfred Haar[1]提出来的，并以他的名字命名为哈尔小波(Haar wavelet)。1988年，Stephane Mallat和伊夫·梅耶尔[2]提出了多分辨率的概念，同年，英格丽·多贝西（Ingrid Daubechies）建立了紧支撑正交小波(compact support orthogonal wavelet)，1989年，Mallat提出了快速小波变换[3]。在小波消噪方面，张维强、宋国乡[4]提出一种新的阈值函数，克服了传统的软硬阈值函数的一些缺点，消噪效果优于传统阈值函数，但是其缺点是阈值函数较传统阈值函数复杂，计算量更大。

管道是一种用于输送气体、液体或带固体颗粒流体的装置，它广泛用在给水、排水、供热、供气、输送石油各种工业装置中[5]。然而管道在运行中也容易发生各种随机振动，对随机振动信号进行分析加工处理是机械设备故障诊断的一项重要手段[6]，但是在振动信号的实际采集过程中，采集的信号夹杂着噪声。这些噪声会对信号的分析和处理产生不利影响，因此如何对信号进行快速有效消噪处理具有重要的现实意义。

本文采用小波理论对输流管道随机振动加速度信号进行信号处理，利用强制和默认两种方法消噪，利用处理后的信号，生成功率谱密度曲线，并进行比较。

2 小波理论

连续小波变换的公式为[7]：

根据Morlet的原始形式，母小波定义为：

小波分析用于信号处理在文献[6]中有着详细的描述。下面简述一下其过程，随机振动信号f(t)是连续的，在小波信号处理中按照Nyquist采样定理取样，因此有f(t)的最优逼近。

其中fJ+1(t)为在小波尺度空间VJ+1上f(t)的逼近或取样信号。采用Mallat分解算法，可将信号分解成

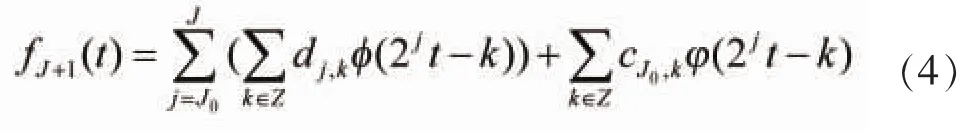
其中，φ（2jt-k）和φ（2jt-k）分别为尺度函数和小波函数，cj,k和dj,k分别称之为逼近系数和小波系数：

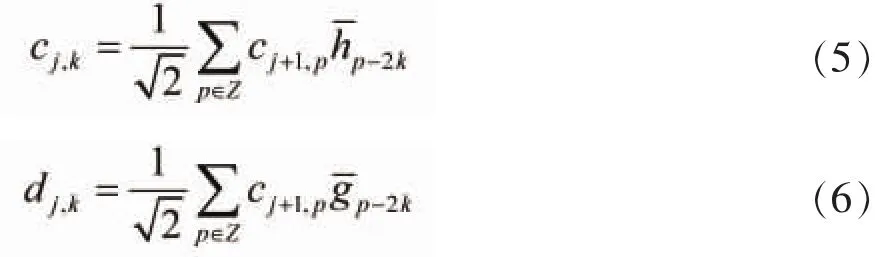
分解之后小波信号处理的本质是修改系数dj,k。

最后利用Mallat算法重构信号

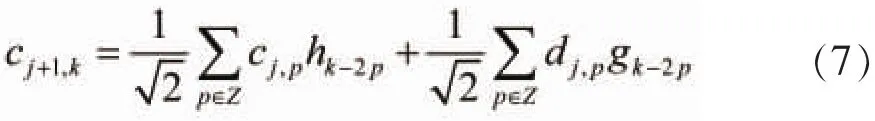
其中hk-2p，gk-2p为双尺度系数。

3 随机振动信号去噪处理过程

小波去噪过程可以分为以下3个步骤[8，9]：

步骤一：一维信号的小波分解。确定所选小波分解层次对其分解计算；本文中选用Daubechies函数族中的db1对其进行3层分解。

步骤二：小波分解高频系数的阈值量化。选定合适阈值，对各个尺度下的高频系数进行量化处理。

步骤三：一维小波重构。根据各层次频率系数进行重构。

最后，通过对比功率谱密度曲线，来观察信号处理效果。功率谱密度谱的物理意义是指单位频率上的能量大小，数学表达式写成：

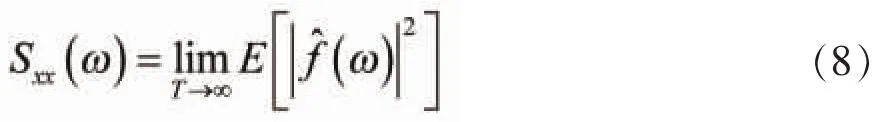
4 随机振动信号去噪实例

对在输流管道上采集的随机振动信号进行处理，采用强制去噪和默认去噪两种方法，最后生成其功率谱密度曲线，进行对比。

图1为采集的加速度原始数据。使用db1对其进行3层分解，并使用强制去噪手段进行消噪[10]，消噪后的图形如图2所示。相关代码如下：

%Use DB1 to decompose the original signal

[c,l]=wavedec(data,3,'db1')；ca3=appcoef(c,l,'db1',3);cd3=detcoef(c,l,3)；cd2=detcoef(c,l,2);

cd1=detcoef(c,l,1)；cdd3=zeros(1,length(cd3))；cdd2=zeros(1,length(cd2))；

cdd1=zeros(1,length(cd1))；c1=[ca3 cdd3 cdd2 cdd1]；s1=waverec(c1,l,'db1')

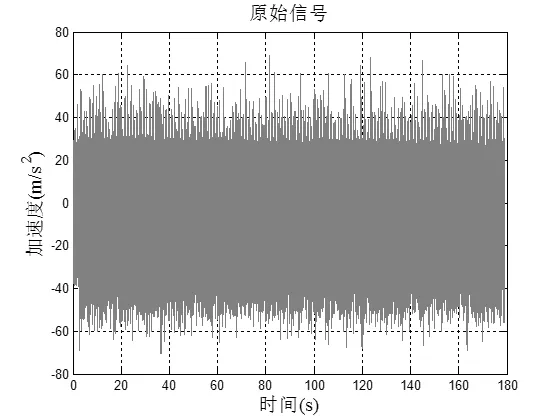
图1 加速度传感器的采集信号

图2 强制消噪后的信号

从图1和图2可以看出，强制消噪后的信号与原始数据相比，已经有很大的不同，消噪之后，信号关于时间轴更加对称，竖轴的数值区间也减小。下面使用默认消噪方法去噪，消噪后信号如图3所示，相关代码如下：

%Use default denoise

[thr,sorh,keepapp]=ddencmp('den','wv',data);

s2=wdencmp('gbl',c,l,'db1',3,thr,sorh,keepapp);

如图3所示，默认消噪后的信号与强制消噪后的图形有些区别，信号落在区间与强制消噪后的区间一致，但保留了更多的信号信息。

图3 默认消噪后的信号

估计功率谱密度曲线(PSD)常有周期图法、Bartlett法、Welch法，由于前两种有局限性，文中采用Welch法[11]，生面的PSD曲线如图4-6。相关代码如下：

[pxx,f,pxxc]=pwelch(s1,window,noverlap,length(s1),Fs,...

'ConfidenceLevel',0.9)

从图4可以看出，未消噪的信号所得到的功率谱密度曲线(PSD)都有较多毛刺，且曲线较为繁复。图5强制去噪后生成功率谱曲线。强制去噪后，曲线相对简单，可以看出可以得出能量较大的频率值，即振动能量最大。但曲线过于光滑，强制去噪容易丢失信息。

图6表示的默认去噪处理后的PSD曲线，也可以得出能量较大的频率值，与先前强制去噪得到的结果是一致的。但与强制去噪对比，更能保持原始信号的形态，更好地保留了信号的信息。

图4 去噪前生成的PSD曲线

图5 强制去噪后的PSD曲线

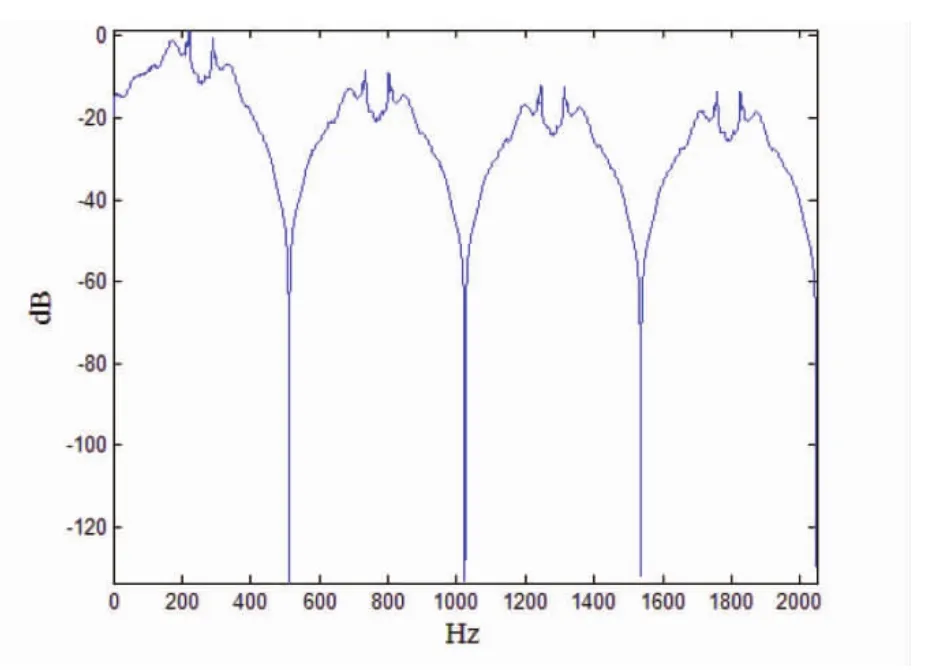
图6 默认去噪后生成的PSD曲线

5 总结

文中利用小波分析法尝试对信号进行了两种不同方式去噪处理，最后Welch法求出功率谱曲线，以此分析信号在各频率上的能量分布。将未进行消噪的信号与用小波消噪的信号功率密度曲线相比较，小波去噪效果强。小波强制去噪会使得信号失真，而默认去噪能很好地保持原有信号形态。小波默认去噪结果比较合适。随机振动信号未去噪之前，功率谱密度曲线复杂且波峰波谷过多，经小波去噪分析之后，更加清晰显示在各个频率上振动能量分布。

[1]Mallat S.A Wavelet Tour of Signal Processing[M].Aca-Demic Press,1999:110-132.

[2]张维强,宋国乡.基于一种新的阈值函数的小波域信号去噪[J].西安电子科技大学学报:自然科学版,2004,31(2):296-299.

[3]白志伟.LPG低温储存装置管道失效分析[D].西安：西安大学，2014：9-10.

[4]姜万录，张淑清，王益群.液压泵故障的小波变换诊断方法[J].机械工程学报，2001，37(6):34-37.

[5]Daubechies I.Ten lectures on Wavelets[M].Society for industrial and applied mathematics,1992：60-85.

[6]Mallat S G.Atheory for Multiresolution Signal Decomposi Tion:the Wavelet Representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(7):674-693.

[7]PaulS.Addison,TheIllustratedWaveletTransform Handbook[J].Institute of Physics,2002(1):117-154.

[8]Oppenheim A V,Schafer,R W.Digital Signal Processing[M].Prentice-hall,lnc,1975:548-554.

[9]彭玉华.小波变换与工程运用[M].北京:科学出版社，1999：100-112.

[10]张德丰.MATLAB小波分析[M].北京：机械工业出版社，2009：40-56.

[11]刘浩.MATLAB R2014a完全自学一本通[M].北京:电子工业出版社，2015：80-92.

Wavelet Denoising Analysis of Acceleration Signals of Random Vibration

Cao Jianhua,Yang Chao
(School of Mechanical and Electrical Engineering,Huangshan University,Huangshan 245041,China)

Vibration is very common in daily life and engineering applications,and vibration signal analysis and processing is an important method of fault diagnosis.However,the acquired signals often contain a variety of noises.How to eliminate the noise is directly related to the next step of diagnosis analysis.The paper makes use of the wavelet to denoise the signals.In order to analyze the vibration of the measurement point,Welch’s method is used to estimate power spectrum curve,which is then compared with PSD curve generated from the original signals.The comparison indicates that power spectrum curve generated from denoised signals can better show the vibration energy at each frequency,which makes it easier for engineering design and diagnosis of fault in mechanical equipments.

digital signal;vibration;MATLAB;wavelet analysis

TN911.7

A

1672-447X(2017)05-0026-004

2017-06-23

曹建华（1983-），江西九江人，黄山学院机电工程学院助教，研究方向为机械振动、小波信号处理；杨超（1994-），安徽寿县人，黄山学院机电工程学院学生，研究方向为小波信号处理。

责任编辑：胡德明