概率论与数理统计微课比赛教案分析

孙晓玲

（合肥师范学院数学与统计学院，安徽合肥230601）

概率论与数理统计微课比赛教案分析

孙晓玲

（合肥师范学院数学与统计学院，安徽合肥230601）

微课教学不同于传统教学，有教学内容少，教学时间短的特点。要在10分钟左右的时间内完成传统授课方式一两节课的内容就需要在录制微课视频之前精心设计微课的教学内容。文章以荣获首届全国高校数学微课程教学设计竞赛一等奖作品“分布函数”为例介绍了概率论与数理统计微课教学的设计思路以及教学过程设计。教学实践表明，微课教学中若能合理设计教学思路，创新教学手段能够起到事半功倍的效果。

分布函数；微课；概率论与数理统计；教学设计；Excel辅助

1 引言

微课教学作为新兴的教学方式这几年得到了较大的发展[1-3]，教育部门举办了各种与微课相关的教育教学交流活动。其中较大的活动为2013年举行的首届全国高校微课教学比赛，2015年举行的首届全国高校数学微课程教学设计竞赛。作为一名高校教师，如何能紧跟教学改革和创新的潮流，将微课与教学实践紧密结合，将微课教学方式与传统教学方式相互补充是现如今教学研究的热点课题[4-7]。

2015年3-8月期间，作者参加了首届全国高校数学微课程教学设计竞赛。该比赛是由参赛教师选择课程中的一个知识点，提交录制完成该点知识的10-20分钟的微课程视频进行参评。讲解的知识点需要符合组委会发布的高等数学、线性代数、概率论与数理统计3门课的知识点目录。要在短时间内完成平时近两节课的授课内容就需要在录制教学视频之前精心设计微课的教学内容。作者讲授的知识点是概率论与数理统计课程中的分布函数。在通常90分钟的课堂上，该节的讲解思路一般是概念引入、定义讲解、例题、小结。在14分19秒的微课教学设计中作者的设计思路成为概念引入、定义、实例以及Excel软件辅助计算。

本文就以作者在首届全国高校数学微课程教学设计竞赛全国决赛中的一等奖获奖作品“分布函数”的教学设计为例，分析概率论与数理统计微课制作的教学方案设计背景以及教学过程设计。

2 概率论与数理统计微课教学设计背景

2.1 教学内容分析

“随机变量的分布函数”既是概率论与数理统计课程中“离散型随机变量及其分布律”教学小结的延伸，又是后面将要学习的“连续型随机变量及其概率密度”教学小结的铺垫，可以起到承上启下的作用。“随机变量的分布函数”是概率论与微积分学的纽带，在概率论中占据着重要的地位。有了分布函数这个桥梁，就能利用微积分这个有利工具研究概率问题。另外，分布函数还是进行统计检验和统计推断的基础，因此该节内容也可为后面数理统计部分的学习打下基础。通过本小节的学习，不仅能让学生掌握概率计算的一般方法，培养学生分析和解决实际问题的能力，还能使学生认识到掌握数学软件比如Excel软件能够对概率论与数理统计课程的学习起到很好的辅助作用。

2.2 学情分析

2.2.1 学生起点知识分析

授课对象是理工科大学二年级的学生，从学生的知识储备上来看，学生已经学过了概率的基本概念以及随机变量的概念，了解了随机变量是用来表示随机现象结果的变量，随机变量的取值表示随机事件。还知道离散型随机变量及其分布，知道二项分布律特点，会计算服从二项分布的随机变量取值的概率。大学一年级已经学过办公自动化课程，了解Excel软件的使用。还不会计算随机变量在任意区间内取值的概率，没有学习计算随机事件概率的一般方法，不了解随机变量的统计规律性。教师若能将授课内容与学生所学专业知识相结合，激起学生的兴趣，调动学习的积极性，教学过程便可水到渠成。

2.2.2 学生心理特征分析

大二学生会对与自己生活息息相关的教学实例感兴趣。本节课将首先从学生的生活实际出发，充分调动学生的思维，从每天的生活费支出情况入手，调动学生学习的兴趣，激发学生的求知欲。

2.2.3 学生能力分析

学生已学过高等数学课程的知识，有一定的数学素养，具有一定的利用数学知识分析问题、解决问题的能力以及利用计算机软件处理数学问题的能力。

有了前期的知识准备，还必须有效调动学生的知识迁移能力。本节课的目的不在知识本身，而是要形成解决问题的过程与方法，通过这节课的学习，培养学生分析问题、解决问题、总结规律的能力，促进学生创新精神和创造能力的培养。

3 教学过程设计

3.1 分布函数的概念

3.1.1 概念引入

先给一个与学生生活贴近的实例激发学生的学习兴趣和求知欲。

创设学习情境：若r.v.x表示某同学大学生活每天的支出，支出分布律如表1所示（单位:元，假设某同学每天的生活支出是随机的并且只有以下5种情况）

表1 生活支出分布律

提问：该同学一天带30元钱够花的概率是多少？

分析：{带30元够花}={≤30}，若该同学一天的支出是10元，20元或30元3种情况，那么一天带30元钱就够花，因此有

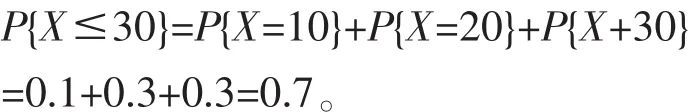
过渡：请同学自己演算“带40元够花的概率”是多少？

分析：“带40元够花的概率”即为

扩展：若要进一步讨论该同学一天带其它钱数够花的概率，可以设一天所带钱数为x，那么该同学带x元够花的概率即为x的函数，可记为F（x），其中F（x）=P{X≤x}。

进一步扩展：对任意实数x，可知P{X≤x}是x的函数，通过P{X≤x}可以计算r.v.X在任意区间内取值的概率。

小结：通过实例引导学生思考随机变量在某区间上取值概率的计算，再由特殊到一般，由浅入深地引申出分布函数的概念。

3.1.2 分布函数的定义

定义[8]：设X为随机变量，对任意实数x，称函数F（x）=P{X≤x}（-∞＜x＜+∞）为随机变量X的分布函数。

关于分布函数概念的两点解释：

1.几何解释：如果将随机变量X的取值看作数轴上随机点的坐标，那么分布函数F（x）在点x处的值就表示随机变量X在区间（-∞，x]内取值的概率。

2.概率的分布函数表示：若随机变量X的分布函数F（x）已知，则对任意实数x1＜x2，随机变量X在区间（x1，x2]内取值的概率可表示为：

P{x1＜x2}=P{X≤x2}-P{X≤x2}-P{X≤x1}=F（x2）-F（x1）；

随机变量X在区间（x1+∞）内取值的概率可表示为：

P{X＞x1}=1-P{x≤x1}=1-F（x1）。

随机变量X在其余任意区间内取值的概率也同样可以用分布函数值来表示，由此可知，只要确定了随机变量X的分布函数，就能计算随机变量X落在任意区间内的概率，即利用分布函数能够完整地描述随机变量的统计规律性。

小结：通过对分布函数定义的解释使学生了解分布函数概念的实质以及概念引入的重要意义。接下来可以让学生分组讨论随机变量在其它任意区间内取值的概率计算公式并总结一般方法，通过分组讨论，培养学生自我解决问题的能力，养成自主学习、小组合作学习的习惯。

3.2 离散型随机变量的分布函数

假设X是离散型随机变量，分布律为P{X=xk}=Pk（k=1，2，3，…），那么其分布函数为F（x）=P{X≤x}=即F（x）是离散型随机变量X取小于等于x的诸值xk的概率之和，故F（x）又被称作累积分布函数[8]。

例1：小李每日开车上班，途经10个路口，每个路口都有交通信号灯，若他在各个路口遇到红灯的事件是相互独立并且概率均为0.7。问：小李上班途中至多遇到6次红灯的概率是多少？

分析：以X表示小李上班途中遇到红灯的次数，可将每次通过路口看作一次随机试验，由于每次遇到红灯的概率相同且每次试验结果相互独立，因此X∶b（10，0.7）。由于随机事件{至多遇到6次红灯}={X≤6}，由二项分布律公式以及离散型随机变量分布函数的计算公式有

小结：通过实例分析及演算使学生掌握计算离散型随机变量分布函数值的步骤，结合实例使学生了解分布函数的实际应用从而为后面连续型随机变量及其分布的讲解埋下伏笔。通过PPT演示的直观图为学生清晰地展现分布函数的计算过程，使学生更深入理解分布函数的概念及计算方法。

按照该方法进行常规计算将会非常复杂，这里可考虑用Excel软件来辅助计算。Excel软件不仅是常用的办公软件，还是很好的数学软件，其中包含了大量的数学函数，是解决概率统计问题的很好的辅助工具，相比于其它常见数学和统计软件来说，Excel软件更容易获取和使用。

利用Excel软件中的二项分布函数：BINOMDIST（m,n,p,L）可直接得到随机变量的分布律和分布函数值，该软件还能够根据所给数据绘出分布律表、分布律柱状图和分布函数的线图。由表2可知若遇到红灯的概率为0.7，则小李至多遇到6次红灯的概率为F（6）=P{X≤6}=0.3504。通过PPT动态展示图1，2能够更清晰地看出概率计算原理及分布函数的意义[9]。

利用Excel演示分布函数值的计算过程不仅能让学生理解分布函数的概念及应用，还能让学生认识到利用Excel软件能够较大程度地提高学习效率、提升学习效果，促进学生创新精神和创造能力的培养。

表2 分布律表

图1 分布律柱状图

图2 分布函数线图

3.3 小结

1.分布函数的概念：F（x）P{X≤x}，（-∞＜x＜+∞）。

2.离散型随机变量分布律与分布函数的关系：

利用关系图总结离散型随机变量分布律与分布函数的关系，能够强化学生对概念的认识和记忆并为下节课的教学内容埋下伏笔。

3.4 作业

1.若X是仅取一个常数值c（c为任意常数）的随机变量，写出它的分布律以及分布函数并画出函数图形。

2.思考：不同的随机变量，其分布函数一定也不相同吗？

通过布置分层作业达到让不同层次的学生进行有效巩固教学内容及其运用的目的，引导学生对随机变量与其分布函数的关系进行思考，从而加深学生对分布函数概念的理解，为后续内容的学习打好基础。

4 结束语

为了能在10分钟左右的时间内完成传统授课方式一两节课的授课内容必须在制作微课之前精心设计微课的教学思路，优化教学内容，创新教学手段以便辅助教学。尽量制作出短小精干、易于网络传播、便于人们学习的优秀微课作为传统课堂的良好补充。根据本文给出的分布函数教学设计方案所制作的微课作品，参加了首届全国高校数学微课程教学设计竞赛全国决赛并获得一等奖，微课辅助课堂教学已在教学实践中进行了检验，取得了较好的教学效果。

[1]刘锐，王海燕.基于微课的“翻转课堂”教学模式设计和实践[J].现代教育技术，2014（5）：26-32.

[2]吴婵.关于微课对优化高校教学效果的思考[J].科教导刊，2013（10）:17-18.

[3]崔静,申广君.大学数学微课教学可行性探究——以概率论与数理统计为例[J].大学教育，2016（6）：169-170.

[4]周丙锋，谢新水，刘星期.高校微课中的教学要素及教学效果评价[J].现代教育技术，2015（9）:30-36.

[5]胡铁生，周晓清.高校微课建设的现状分析与发展对策研究[J].现代教育技术，2014，24（2）:5-13.

[6]史娜，薛亚奎，雷英杰，等.翻转课堂在《概率论与数理统计》课程中的教学设计研究[J].兰州文理学院学报：自然科学版，2015（6）：94-98.

[7]钟绍春，张琢，唐烨伟.微课设计和应用的关键问题思考[J].中国电化教育，2014（12）：85-88.

[8]峁诗松，程依明，濮晓龙.概率论与数理统计教程（第二版）[M].北京：高等教育出版社，2011：61-65.

[9]孙晓玲，王宁.Excel软件辅助概率论与数理统计教学[J].合肥师范学院学报，2015（3）：73-76.

An Analysis on the Teaching Plan of Micro-lectures for Probability Theory and Mathematical Statistics

Sun Xiaoling
(School of Mathematics and Statistics,Hefei Normal University,Hefei 230601,China)

Different from traditional teaching,micro teaching has the characteristics of short teaching time and little teaching content.In order to complete the teaching content of one or two classes according to traditional teaching method in ten minutes or so,the content of the course will need to be carefully designed before recording micro lesson videos.The design ideas and teaching process design of micro teaching for Probability Theory and Mathematical Statistics is introduced by taking the micro lecture of"distribution function"which has won the first prize in the First National College Mathematics Micro Curriculum Teaching Design Competition as an example in this paper.The teaching practice shows that if teaching ideas are reasonably designed,and teaching methods are innovated in micro teaching,then twice as much can be accomplished with half the effort.

distribution function;micro lectures;Probability Theory and Mathematical Statistics;teaching design;Excel-aided

G642.0

A

1672-447X（2017）03-0107-004

2017-01-13

安徽省教育厅质量工程项目（2016gkk027）

孙晓玲（1977-），安徽合肥人，合肥师范学院数学与统计学院副教授，研究方向为不确定性模糊推理。

责任编辑：胡德明