反倾层状岩土复合边坡的稳定性分析方法

郭建军，王俊杰，黎洪光

(1.重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074；2.重庆水利电力职业技术学院，重庆 402160)

反倾层状岩土复合边坡的稳定性分析方法

郭建军1，2，王俊杰2，黎洪光1

(1.重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074；2.重庆水利电力职业技术学院，重庆 402160)

根据极限平衡理论，结合悬臂梁模型，提出了一种简易的岩土复合的滑动-弯曲倾倒破坏的理论分析方法。利用库伦土压力理论分析了上覆土体对下卧岩层的作用力，结合悬臂梁模型和协调平衡原理，引入重度增大系数，求得了下卧反倾层状软岩在上覆土体作用力下的稳定安全系数的解析表达式。结合实例验证了所提方法的正确性。所给出的理论分析方法有益于快速判断此类边坡的稳定性。

岩土工程；反倾边坡；岩土复合；弯曲倾倒； 稳定性分析

0引言

岩石边坡可能失稳破坏的形式有很多种，倾倒破坏是一种典型形式。目前国内外对倾倒变形的研究主要集中于块状倾倒和弯曲倾倒破坏模式。主要研究方法包括极限平衡方法和数值分析方法(有限单元法、非连续变形分析(DDA)以及流形元方法等)，而极限平衡法则是岩质边坡倾倒破坏稳定性分析最常用的方法。1976年，R.E.GOODMAN等[1]提出了基于极限平衡原理的边坡块状倾倒稳定分析方法(简称G-B法)。C.W.DUNCAN[2]在G-B模型的基础上，增加了作用于板状岩体层间和倾倒岩体底面上的水压力，以及在倾倒体上部外荷载的作用，并给出了其基本解析式。李天扶[3]基于C.W.DUNCAN的工作，建议水压力应按水柱的垂直高度计算的思路。陈祖煜等[4]针对G-B法进行改进，考虑了岩柱底滑面的连通率，以及底面和侧面不正交的一般情况，并改进了破坏模式的判定方法。汪小刚等[5]针对G-B法，进一步考虑了岩体结构面的具体分布特征。A.BOBET[6]假定块体厚度很小，对块状倾倒模式进行了无渗流和有渗流两种情况下极限平衡方法的探讨。王建锋等[7]根据Scavia模型[8]，给出了由台阶状破坏面上柱状岩块所组成的具有潜在旋转-倾倒破坏模式的完整改进理论解。

Ö.AYDAN等[9]提出了倾倒破坏的悬臂梁模型。C.SAGASETA等学者[10-15]对悬臂梁极限平衡计算模型进行了改进和完善。如M.AMINI等[12]根据悬臂梁模型，结合极限平衡方程，借鉴梁弹性变形的控制方程，推导了弯曲倾倒岩层的相互作用力。2011年，A.MAJDI等[13]引入新的参数，运用固体力学和断裂力学方法对悬臂梁模型进行了修正。A.K.ALZO′UBI等[16]用离心试验和数值模拟分别讨论了岩层的抗拉强度在弯曲倾倒破坏中的重要作用，否认了内摩擦角的决定性作用。A.L.PINHEIRO等[17]用离散单元法对某具体边坡的弯曲倾倒破坏进行模拟研究。ZHAO Li等[18]基于连续介质的离散元法，模拟了抚顺某大型反倾边坡的弯曲倾倒破坏特征、机理和演变过程，用强度折减法(SSR)表达岩体强度恶化，同时用现场测量的数据进行验证。

刘才华等[19-20]基于极限平衡理论，提出了岩质边坡块体倾倒破坏稳定的传递系数法。杨保军等[21]采用改进的传递系数法，提出了岩质边坡滑动-倾倒组合破坏的解析方法。

虽然针对边坡的岩块倾倒破坏模式和弯曲倾倒破坏模式的研究工作比较多，但是针对其岩块-弯曲倾倒破坏模式却少见报端[22]。在已有的研究工作中，岩层的自重是导致倾倒破坏的主要因素，然而也有其他因素导致倾倒破坏(例如，地震作用、地下水的作用及岩石边坡坡肩后方土体的压力作用等)。在工程实际中，这种单纯的岩质边坡发生倾倒破坏的案例虽然不少，但更为普遍的是在反倾岩层后方存在覆盖土层(图1)[23]。覆盖层可能是原有岩层风化的产物，也可能是后期形成的第四系堆积物。根据上覆土层的性质区分，其可能发生圆弧滑动破坏或者直线滑动破坏，而下卧层状岩层可能发生弯曲倾倒破坏，这种破坏形式可以被称为岩土复合的滑动-弯曲倾倒破坏形式。笔者根据极限平衡理论，结合悬臂梁模型，提出了一种简易的岩土复合的滑动-弯曲倾倒破坏的理论分析方法。

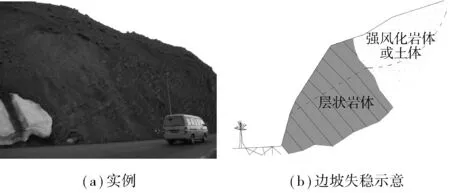
图1岩土复合反倾边坡实例及其失稳破坏示意Fig.1An example for anti-inclined and layered slope with rock and soil composition and its failure schematic diagram

1上覆土体的压力分析

上覆土体在自重及外荷载作用下，产生向下滑动趋势，并作用于下卧层状岩体。上覆土体可能是黏性土体、非黏性土体，或者是岩层风化形成松散碎屑堆积物，其中黏性土体可能沿潜在的圆弧滑动面产生滑动，非黏性土体和松散堆积物可能产生楔形体滑动(图2)。

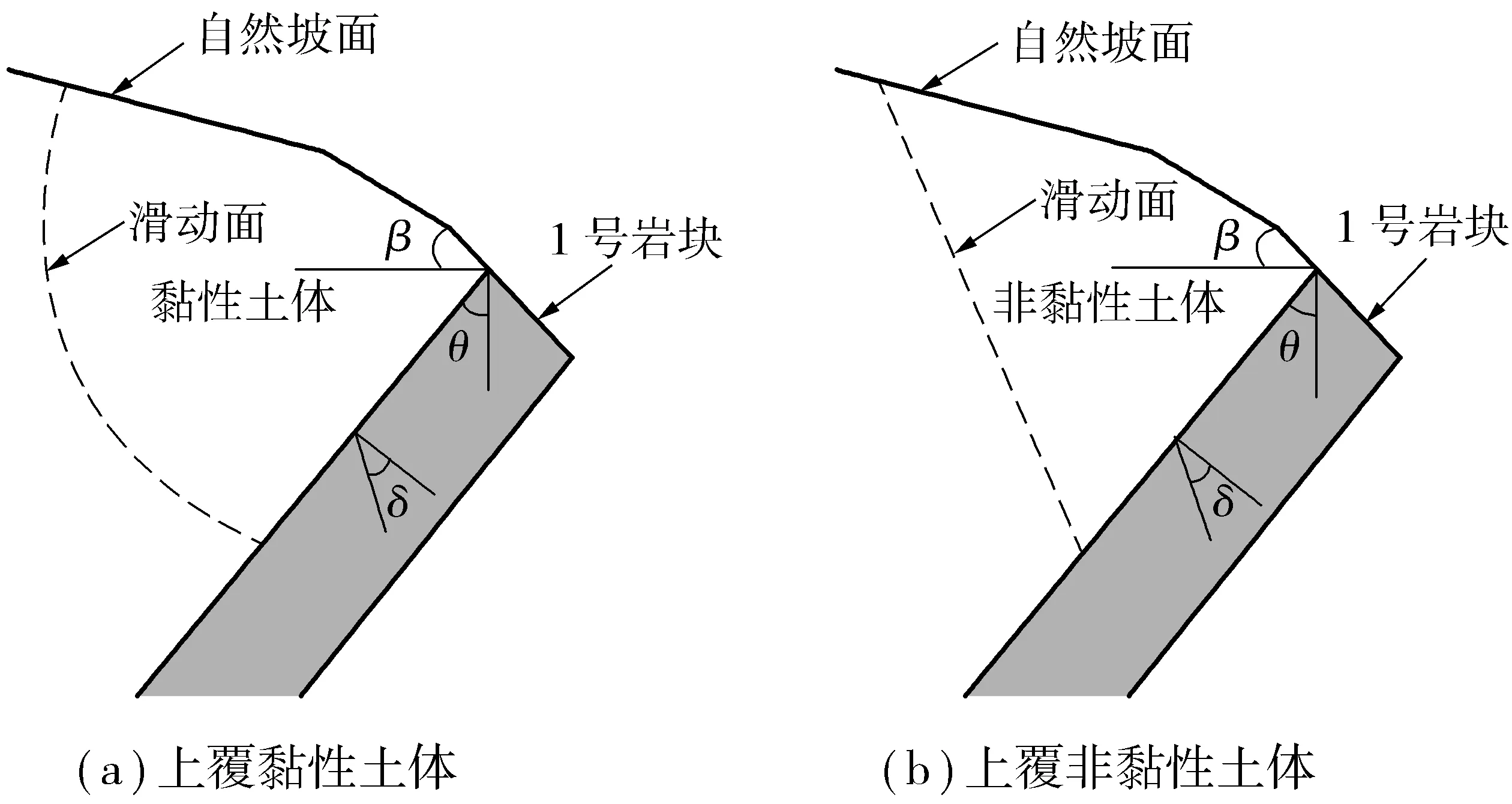
图2上覆土体滑移破坏的地质力学模型Fig.2Geology mechanical model for sliding failure of overlying soil

下卧岩层类似于挡土墙，θ为下卧岩层面与竖直面的夹角，θ的变化范围是0°≤θ≤90°，当θ=90°，上覆土体对下卧岩层的作用力应等于上覆土体的重力，且近似均匀分布。当θ≤θcr时，且下卧岩层在上覆土体的作用下产生弯曲变形和位移时，上覆土体作用于下卧岩层的力的大小近似等于主动土压力[24]。θcr是下卧岩层面与竖直面的临界夹角，它与岩层与土体的摩擦角δ，土体的内摩擦角φ，以及土体坡角β等因素有关。当δ=φ时，θcr可以用下式表达：

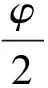
E.MOHTARAMI等[23]在V.V.SOKOLOVSKII 和W.F.CHEN等[24-25]工作基础上，根据塑性理论，考虑速度分量，结合一定假设，得到了主动土压力系数，并与库伦主动土压力系数和有限元分析结果进行了比较，3者吻合。所以，当θ≤θcr时，可以采用库伦主动土压力系数计算上覆土体作用于下卧岩层的作用力大小，并且假定呈三角形分布，库伦主动土压力的方向在下卧岩层上表面法线上方，并与岩层面法线成δ角或与水平面成θ+δ角(图3)。

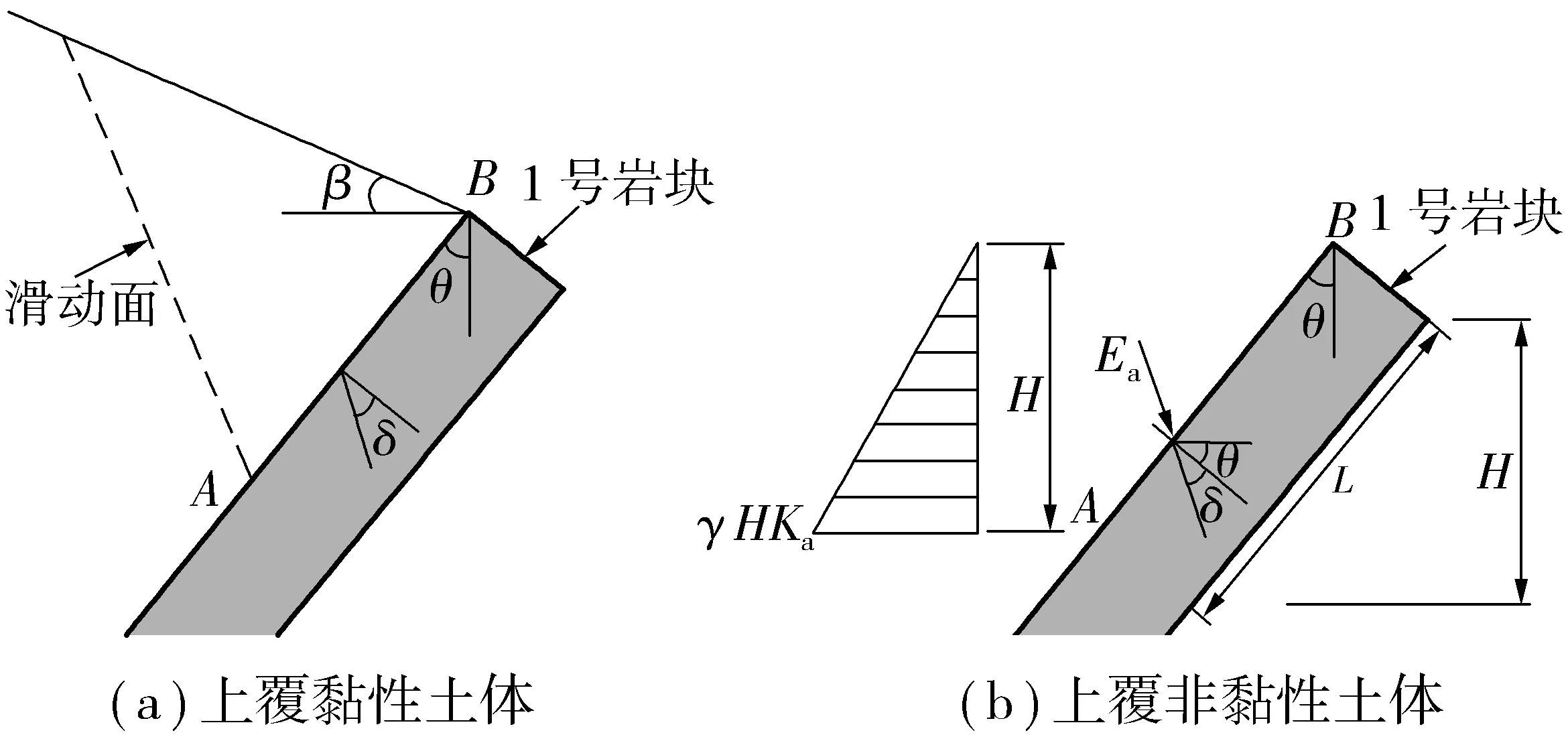
图3库伦主动土压力强度分布Fig.3Coulomb active earth pressure intensity distribution

作用于下卧岩层上总主动土压力Ea的大小为

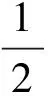
(1)

式中：Ka为库伦主动土压力系数；γ为上覆土体的重度；H为下卧岩层受压区域的竖直投影高度，H=Lcosθ。

在黏性土中：

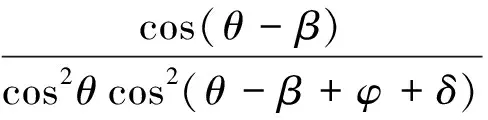
{Kq[cos(θ-β)cos(θ+δ)+sin(φ+δ)sin(φ-β)]+

2ηcosθcosφsin(θ-β+φ+δ)-

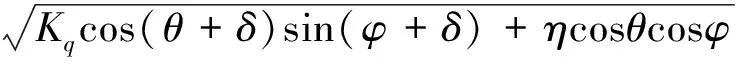
(2)

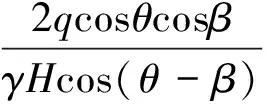
(3)

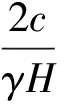
(4)

在非黏性土中：

Ka=

(5)

将主动土压力分解到下卧岩层上表面法线方向，得到下卧岩层上表面(AB面)任意点F的法线方向分力为PF=γxKacosδ·cotθ，x为F点到B点的水平距离，x的取值范围是x∈[0，Lsinθ]。下卧岩层将在此分布力及自身重力作用下发生弯曲倾倒变形破坏(图4)，上覆土体作用于下卧岩层AB面上法线方向的合力为

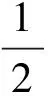
(6)

图4下卧岩层表面法向压力分布(θ≤θcr)Fig.4Normal pressure distribution on the lying rock surface (θ≤θcr)

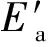
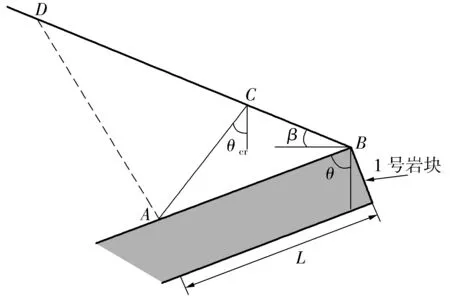
图5上覆土体分区示意图(θ>θcr)Fig.5Overlying soil zoning map(θ>θcr)

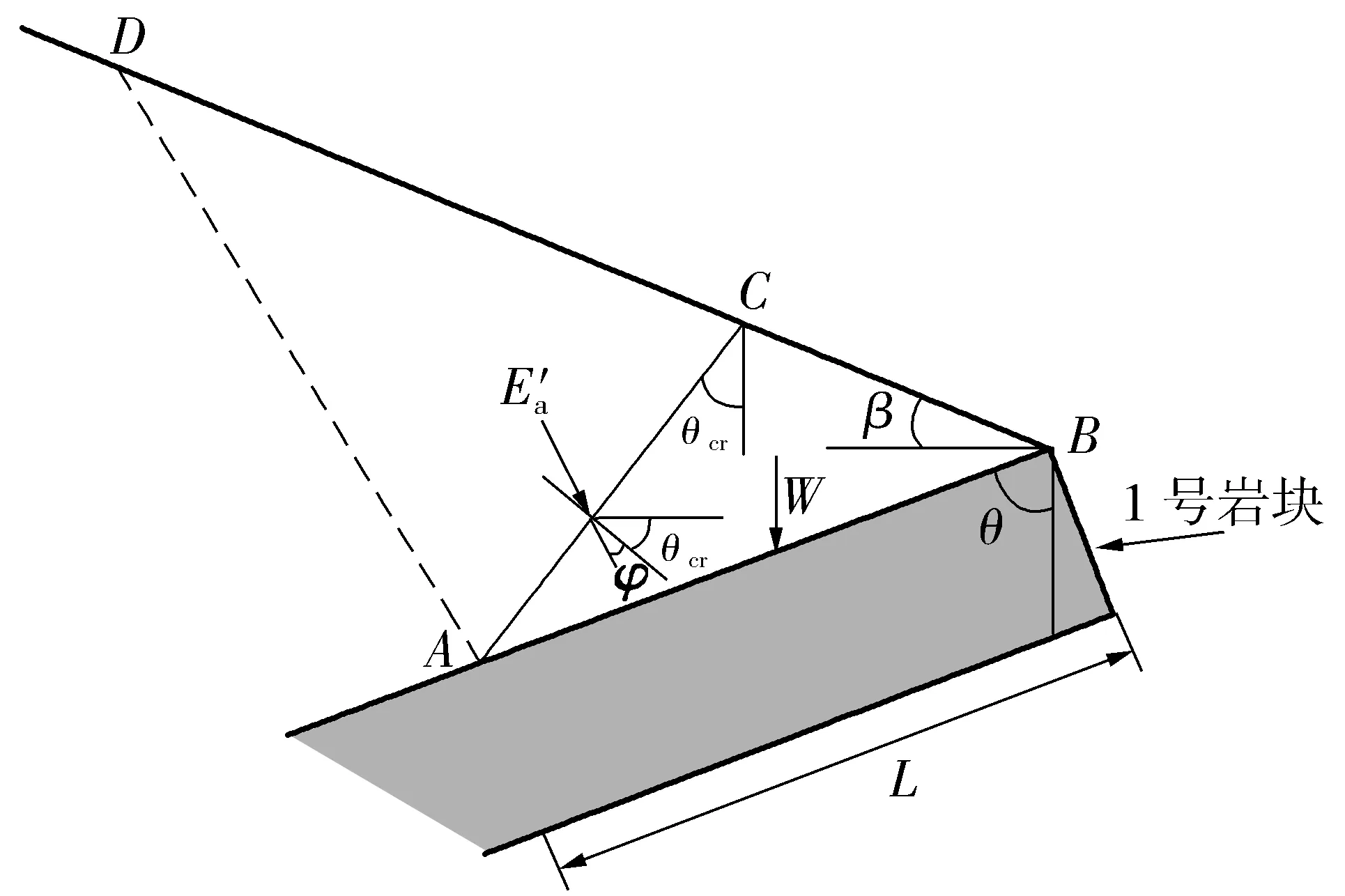
图6下卧岩层表面所受作用力示意(θ>θcr)Fig.6Schematic of the force on the lying rock surface(θ>θcr)

则上覆土体作用于下卧岩层AB面上法线方向的合力为

(7)

2下卧岩层弯曲倾倒破坏分析

下卧岩层弯曲倾倒的本质原因是弯曲引起的拉应力在岩层最大弯矩点产生拉裂缝造成的。Ö.AYDAN等[9]提出的悬臂梁模型是分析这种破坏模式的方式之一，已有的悬臂梁模型建立的基础包含以下几点假设：

1) 每层岩层被看作是在边界力和自重作用下的悬臂梁，边界上的力简化为集中力；

2) 边坡岩体存在一个基准面，所有基准面以上岩层都处于极限平衡状态，在极限平衡状态下，作用在基准面上的最大拉应力等于岩层材料的抗拉强度，基准面与层面法线方向呈一定角度；

3) 岩层间的剪切力只考虑层间内摩擦力，而不考虑层间黏聚力。

然而根据前文的分析，1号岩块上所受的边界力并不是集中力，而是一个分布力。同时，由于下卧软岩的弯曲倾倒变形破坏过程并不仅取决于最大拉应力等于岩层材料的抗拉强度的假定基准面，可能存在多个最大拉应力等于岩层材料的抗拉强度的点，导致各岩层上表面开裂，并形成塑性弯曲，所以将各岩层之间的相互作用力当作分布荷载考虑更为合理。

1号岩块以下各岩层在上覆岩层传递的分布荷载和自身重力作用下发生弯曲变形，同时在岩层的各横截面上产生压应力和拉应力，如果岩层横截面上受拉区各点的拉应力超过了岩石的抗拉强度，那么岩层将发生破坏。由于各岩层发生了塑性弯曲变形，岩层之间传递的内力的分布形式难以用单一的函数描述。M.AMINI等[12]绕开了求解岩层之间的内力传递的具体分布函数，根据整体协调平衡理论，利用几何及三角函数关系推导了反倾软岩层在自重作用下的稳定性系数Fs：

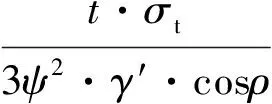
(8)

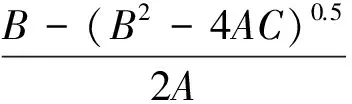
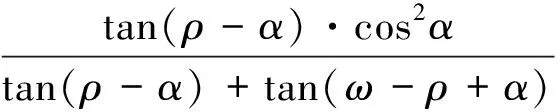
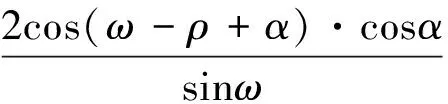
式中：σt为岩体的抗拉强度；γ′为岩层的重度；ρ为反倾岩层的倾角；α为岩层破坏基准面与岩层面法线方向的夹角；ω为边坡坡面与水平面的夹角；t为岩层的厚度；h为坡体的高度(图7)。

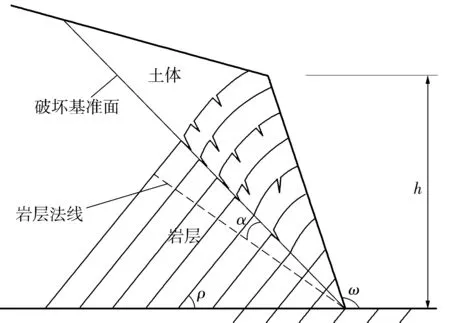
图7弯曲倾倒破坏的层状岩土复合边坡Fig.7Flexural toppling failure of layered slope with rock and soil composition

从宏观的角度分析，下卧岩层在上覆土体的重力作用下，岩层之间传递的内力包括岩层的自重应力和上覆土体的作用力两部分，但是各层之间传递力的具体分布形式不能精确描述，整个下卧岩层在发生弯曲倾倒的过程中，内力不断调整，协调平衡，最终由于整体平衡不能维持而发生弯曲倾倒破坏，所以在Amini工作基础上，将上覆土体的荷载以重度增大系数Zγ的形式引入到稳定性系数Fs中，即

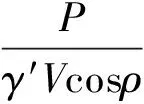
(9)

γ″=γ′·(1+Zγ)

(10)

(11)

式中：P为上覆土体作用于1号岩块上表面法线方向的合力(取为P1，P2)；V为弯曲倾倒破坏岩层的总体积。

在分析反倾层状岩石边坡的稳定性时，悬臂梁极限平衡分析模型是根据悬臂梁弯曲模型，利用极限平衡理论，假定各岩层间的相互作用力为集中力，从最上部的岩层算起，推到最下面的岩层，建立各自的力矩平衡方程，通过迭代的方法求解出反倾边坡坡脚剩余下滑力，即通过剩余下滑力判断边坡稳定性的分析方法。结合边坡实际破坏过程，通过前述分析可以得出，悬臂梁极限平衡分析模型中的假定(各岩层间的相互作用力为集中力)与该类边坡的实际破坏模式有较大的出入；而且悬臂梁弯曲模型中判断某一层是否产生倾倒的条件是该岩层在破坏基准面处的最大拉应力超过了岩石的抗拉强度，实际上，下卧软岩的弯曲倾倒变形破坏过程并不仅取决于最大拉应力等于岩层材料的抗拉强度的假定基准面，可能存在多个最大拉应力等于岩层材料的抗拉强度的点，导致各岩层上表面开裂，并形成塑性弯曲，各岩层之间相互作用，协调平衡，当整体平衡失稳时，边坡即发生破坏，如图7。同时笔者所提出的分析方法力学模型清楚、计算过程简便，有利于在实际工程应用和推广。

3应用实例分析

某公路边坡[23]如图8。

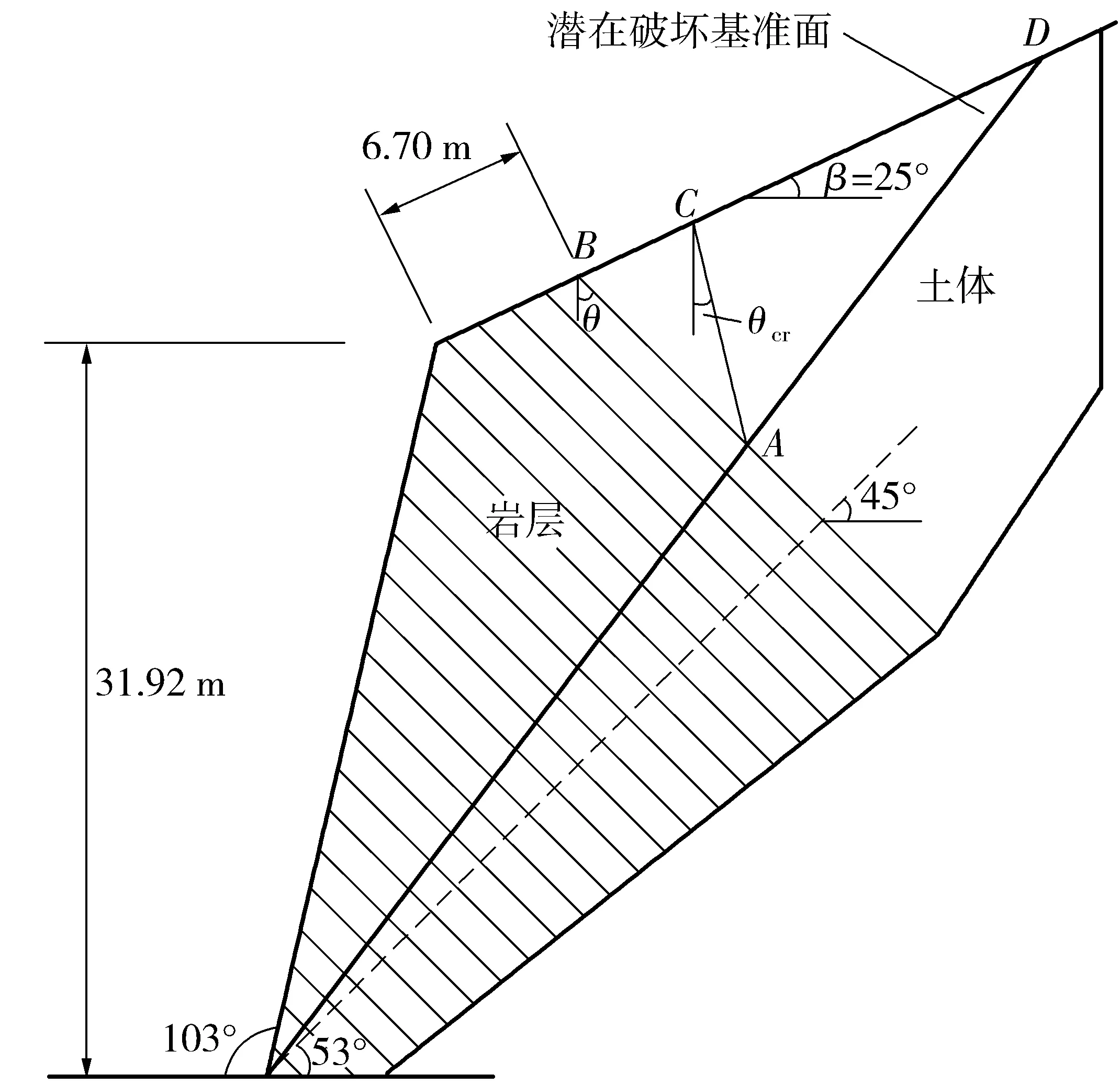
图8弯曲倾倒破坏的岩土复合边坡实例Fig.8A case study of the flexural toppling failure of layered slope with rock and soil composition

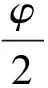
(12)

在饱和情况下，单位宽度三角形土体ABC重力为

W=γsat·VABC=19.68×26.60=523.488 (kN)

(13)

则上覆土体作用于下卧岩层AB面上法线方向的合力为

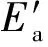
(14)

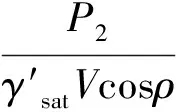
(15)

γ″=γ′·(1+Zγ)=30.927 4 (kN/m3)

(16)

代入式(11)计算得到该岩土复合的边坡的安全系数为

(17)

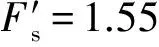
4结语

倾倒破坏是反倾岩质边坡破坏的一种典型破坏形式，反倾层状岩土复合边坡的稳定性研究还少见报端。笔者提出了一种简便的求解上覆土体、下卧反倾层状岩石的复合边坡的稳定性分析方法。利用库伦土压力理论分析了上覆土体对下卧岩层的作用力，结合悬臂梁模型和协调平衡原理，引入重度增大系数，求得了下卧反倾层状软岩在上覆土体作用力下的稳定安全系数的解析表达式。笔者所给出的理论分析方法有益于快速判断此类边坡的稳定性。

[1] GOODMAN R E，BRAY J W.Toppling of rock slopes[C]//ProceedingsoftheSpecialityConferenceonRockEngineeringforFoundationsandSlopes.Colorado：[s.n.]，1976：201-234.

[2] DUNCAN C W.FoundationsonRock[M].2nd ed.London：SPONEFN，1999.

[3] 李天扶.论层状岩石边坡的倾倒破坏[J].西北水电，2006 (3)：4-6.

LI Tianfu.On tilting failure of bedded rock slope[J].NorthwestHydropower，2006(3)：4-6.

[4] 陈祖煜，张建红，汪小刚.岩石边坡倾倒稳定分析的简化方法[J].岩土工程学报，1996，18(6)：92-95.

CHEN Zuyu，ZHANG Jianhong，WANG Xiaogang.A simplified method for stability analysis of rock slope[J].ChineseJournalofGeotechnicalEngineering，1996，18(6)：92-95.

[5] 汪小刚，贾志欣，陈祖煜，等.岩质边坡倾倒破坏的稳定分析方法[J].水利学报，1996(3)：7-12.

WANG Xiaogang，JIA Zhixin，CHEN Zuyu，et al.The research of stability analysis of toppling failure of jointed rock slopes[J].JournalofHydraulicEngineering，1996(3)：7-12.

[6] BOBET A.Analytical solutions for toppling failure[J].InternationalJournalofRockMechanicsandMiningScience，1999，36：971-980.

[7] 王建锋，Wilson H Tang，崔政权.块状岩体边坡倾倒破坏稳定性分析[J].中国地质灾害与防治学报，2001，12(4)：1-8.

WANG Jianfeng，Wilson H Tang，CUI Zhengquan.Stability analysis of toppling failure of block rock slopes[J].TheChineseJournalofGeologicalHazardandControl，2001，12(4)：1-8.

[8] SCAVIA C，BARLA G，BERNAUDO V.Probabilistic stability analysis of block toppling failure in rock slopes[J].InternationalJournalofRockMechanics&MiningSciences，1990，27(6)：465-478.

[9] AYDAN Ö，KAWAMOTO T.The stability of slopes and underground openings against flexural toppling and their stabilisation[J].RockMechanicsandRockEngineering，1992，25(3)：143-165.

[10] SAGASETA C，SNCHEZ J M，Caizal J.Corrigendum to：“A general analytical solution for the required anchor force in rock slopes with toppling failure”[J].InternationalJournalofRockMechanics&MiningSciences，2006，43(2)：336-336.

[11] MAJDI A，AMINI M.A new analytical method for analysis of flexural toppling failure in rock slopes[J].InteractiveCardiovascular&ThoracicSurgery，2008，3 (1) ：2-13.

[12] AMINI M，MAJDI A，ÖMER AYDAN.Stability Analysis and the Stabilisation of Flexural Toppling Failure[J].RockMechanicsandRockEngineering，2009，42(5)：751-782.

[13] MAJDI A，AMINI M.Analysis of geo-structural defects in flexural toppling failure[J].InternationalJournalofRockMechanics&MiningSciences，2011，48(2)：175-186.

[14] 卢海峰，刘泉声，陈从新.反倾岩质边坡悬臂梁极限平衡模型的改进[J].岩土力学，2012，33(2)：577-584.

LU Haifeng，LIU Quansheng，CHEN Congxin.Improvement of cantilever beam limit equilibrium model of counter-tilt rock slopes[J].RockandSoilMechanics，2012，33(2)：577-584.

[15] 张以晨，佴磊，沈世伟，等.反倾层状岩质边坡倾倒破坏力学模型[J].吉林大学学报(地球科学版)，2011，41(增刊1)：207-213.

ZHANG Yichen，NAI Lei，SHEN Shiwei，et al.Mechanical models of anti-dip layered rock slope toppling failure[J].JournalofJilinUniversity(EarthScienceEdition)，2011，41(Sup1)：207-213.

[16] ALZO’UBI A K，MARTIN C D，CRUDEN D M.Influence of tensile strength on toppling failure in centrifuge tests[J].InternationalJournalofRockMechanics&MiningSciences，2010，47(6)：974-982.

[17] PINHEIRO A L，LANA M S，SOBREIRA F G.Use of the distinct element method to study flexural toppling at the Pico Mine，Brazil[J].BulletinofEngineeringGeologyandtheEnvironment，2015，74(4)：1177-1186.

[18] ZHAO Li，WANG Jinan，LI Lin，et al.A case study integrating numerical simulation and GB-InSAR monitoring to analyze flexural toppling of an anti-dip slope in Fushun open pit[J].EngineeringGeology，2015，197：20-32.

[19] LIU C H，JAKSA M B，MEYERS A G.A transfer coefficient method for rock slope toppling[J].CanadianGeotechnicalJournal，2009，46(1)：1-9.

[20] LIU C H，JAKSA M B，MEYERS A G.Toppling mechanisms of rock slopes considering stabilization from the underlying rock mass[J].InternationalJournalofRockMechanicsandMiningSciences，2010，47(2)：348-354.

[21] 杨保军，何杰，吉刚，等.岩质边坡滑动-倾倒组合破坏模式稳定性分析[J].岩土力学，2014，35(8)：2335-2341.

YANG Baojun，HE Jie，JI Gang，et al.Stability analysis of sliding-toppling complex failure of rock slope[J].RockandSoilMechanics，2014，35(8)：2335-2341.

[22] AMINI M，MAJDI A，VESHADI M A.Stability analysis of rock slopes against block-flexural toppling failure[J].RockMechanicsandRockEngineering，2012，45(4)：519-532.

[23] MOHTARAMI E，JAFARI A，AMINI M.Stability analysis of slopes against combined circular-toppling failure[J].InternationalJournalofRockMechanics&MiningSciences，2014，67(2)：43-56.

[24] SOKOLOVSKII V V.Statics of granular media[J].JournalofAppliedMechanics，1965，33(1)：239.

[25] CHEN W F，ROSENFARB J L.Limit analysis solutions of earth pressure problems[J].Soils&Foundations，1973，13(4)：45-60.

(责任编辑：谭绪凯)

Stability Analysis Method for Anti-inclined and Layered Slopes with Rock and Soil Composition

GUO Jianjun1, 2, WANG Junjie1, LI Hongguang2

(1. National Engineering Research Center for Inland Waterway Regulation, Chongqing Jiaotong University, Chongqing 400074, P. R. China; 2. Chongqing Water Resources and Electric Engineering College, Chongqing 402160, P. R. China)

Based on the limit equilibrium theory and the cantilever beam model, a simple theoretical analysis method for toppling failure of rock and soil composite structures was proposed. Firstly, the force on the lying rock from the overlying soil was analyzed, according to Coulomb’s earth pressure theory and Tan wall theory. Secondly, with flexural cantilever model and coordinate the equilibrium equation, increasing factor of weight was introduced, and the analytic expression of the stability safety factor for anti-inclined and layered slopes with rock and soil composition was solved. At last, a case study was used to verify the correctness of the proposed method. The presented theoretical analysis method is beneficial to judge the stability of this kind of slopes quickly.

geotechnical engineering; anti-inclined slope; rock and soil composition; flexural toppling; stability analysis

TU452

A

1674-0696(2017)10-070-06

2016-10-03；

2017-03-22

国家科技支撑计划课题(2015BAK09B01)；重庆市基础与前沿研究计划项目(重点)(cstc2015jcyjBX0139)；重庆交通大学国家内河航道整治工程技术研究中心暨水利水运工程教育部重点实验室开放基金项目(SLK2015B03)

郭建军(1986—)，男，四川南充人，讲师，博士研究生，主要从事边坡工程方面的研究。E-mail：guofuzhi@126.com。

王俊杰(1973—)，男，甘肃陇西人，教授，博士生导师，主要从事岩土、地质工程方面的研究。E-mail：wangjunjiehhu@163.com。

10.3969/j.issn.1674-0696.2017.10.12