基于FastICA改进EMD的算法研究

付 春， 孙祥磊， 王 昆， 管海伟， 刘 娟， 李 明

(1.辽宁石油化工大学 石油天然气工程学院,辽宁 抚顺 113001； 2.沈阳建筑大学 土木工程学院,辽宁 沈阳 110168)

基于FastICA改进EMD的算法研究

付 春1， 孙祥磊1， 王 昆1， 管海伟1， 刘 娟1， 李 明2

(1.辽宁石油化工大学 石油天然气工程学院,辽宁 抚顺 113001； 2.沈阳建筑大学 土木工程学院,辽宁 沈阳 110168)

经验模态分解(EMD)算法在非线性、非稳态的信号处理上具有显著的优势，但EMD在实际应用过程中存在着一些缺陷，其中以模态混叠和虚假模态现象最为突出。模态混叠现象可以简单地概述为在1个本征模函数(IMF)含有多于一阶的结构固有模态分量；虚假模态现象则是指不该有的频率组分对结构模态参数识别精度的严重影响。针对这一问题，对EMD中存在的以上两大缺陷展开研究，提出了利用频带滤波和独立分量分析算法(ICA)中的快速ICA算法(FastICA)相结合改进的EMD算法。利用希尔伯特变换(HT)识别结构频率，并通过Benchmark结构验证了所提算法的有效性。

经验模态分解(EMD)； 盲源分离(BSS)； 模态混叠； 希尔伯特变换(HT)

1998年，N.E.Huang等创造性地提出了经验模态分解算法(Empirical Mode Decompositon,EMD)，该算法一经提出就在不同领域得到了广泛应用[1-3]。然而随着EMD算法应用的增多，其分解过程中存在的模态混叠及虚假模态现象尤为突出，为此很多学者对经典EMD算法进行改进研究[4-8]。

近些年，盲源分离 (Blind Signal Separation, BBS)[9-10]越来越多地被应用在各个领域的研究中，BBS根据统计独立的思想，将多个观测信号借助于优化算法分解为若干个独立的成分，达到信号增强的目的，以便对信号进行合理的分析。独立分量分析算法 (Idenpendent Component Analysis, ICA)[11-13]是盲源分离中的常用算法，并在盲信号处理领域中得到了广泛的应用。目前，ICA理论比较成熟，并在混叠信号独立源的分离方面具有突出的优势。经过EMD分解之后，理论上每个本征模函数(Intrinsic Mode Function，IMF)在任意时刻都应该是仅有的单一振荡模式，每个时刻都具有与其他IMFs不同的单一瞬时频率。因此，理论上各IMF之间应该是相互独立的。本文将ICA中的一种快速ICA算法FastICA算法[14-16]引入到频带滤波改进EMD的分解过程中，作为真正IMFs的判定工具，利用ICA中的FastICA算法实现IMF的自动识别，即将EMD分解后真正IMF的判定标准转换成对IMFs混合信号独立源的求解问题，FastICA分离得到的独立分量即为真正的IMFs。

1 FastICA算法

盲源分离属于盲信号识别的范畴，适用于源信号和传输通道参数均未知的情形。其识别原理是按照源信号的统计特性，从m个观测信号x(t)=(x1,x2,…,xm)中分离出n个源信号s=(s1,s2,s3,…,sn)中含有的各独立成分。即通过确定分离矩阵W，获得源信号s的合理估计。

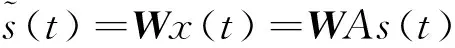
(1)

FastICA算法，又被称为固定点算法，是ICA的一种快速算法。与神经网络算法不同，FastICA算法属于批处理算法，是一种快速寻优迭代算法，其收敛速度比纯粹的批处理算法甚至自适应处理算法更快，并因此而得名。FastICA算法分为基于峭度、似然最大和负熵最大等形式。本文采用基于负熵判据的ICA固定点算法。

FastICA算法具体推导过程详见文献[14-16]，算法实现过程如图1所示。

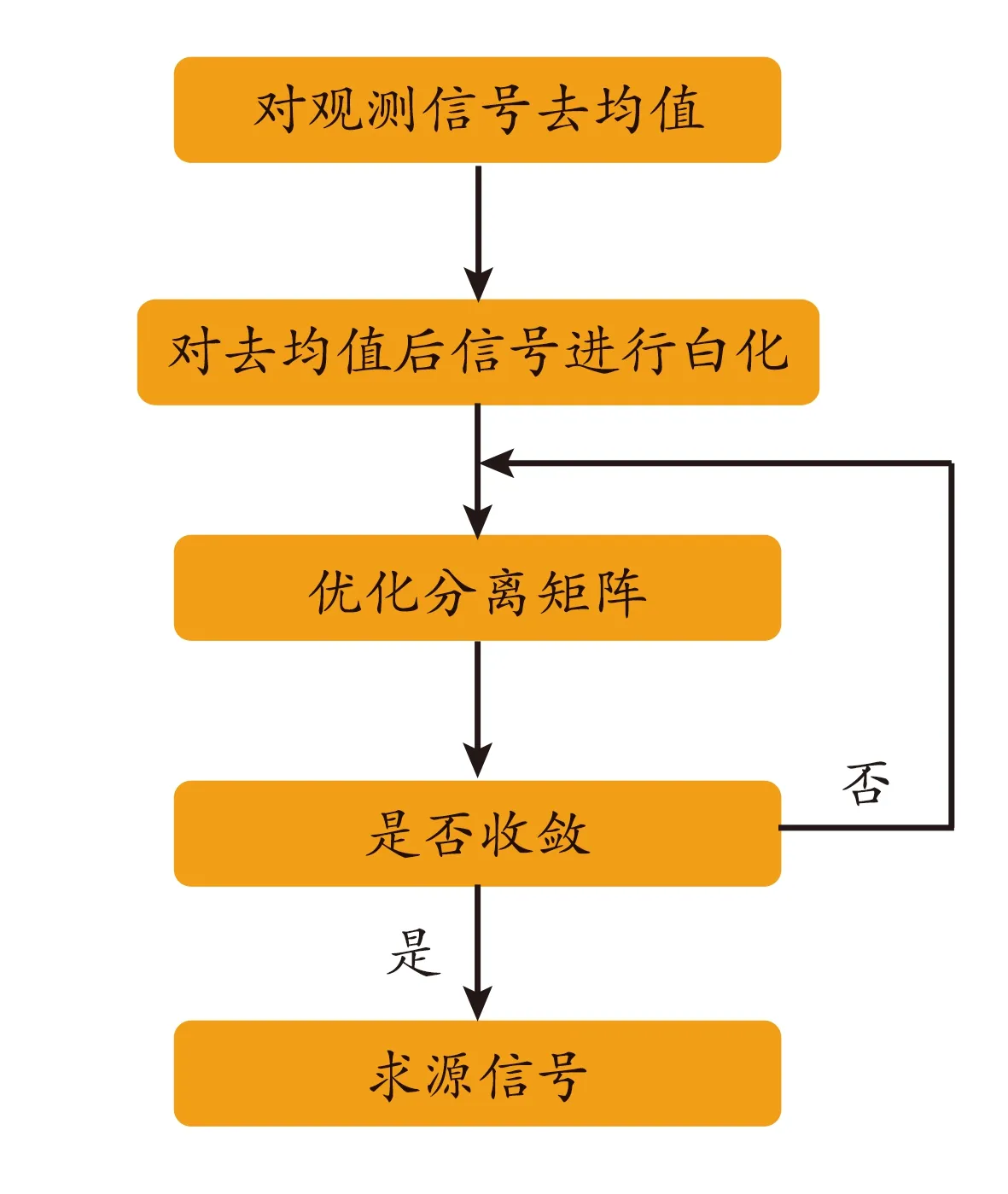
图1 FastICA算法流程图

若要估计源信号中的n个独立分量，则要重复进行上述FastICA算法过程n次，即每当分离出1个独立分量，便从待分析信号中减去此分离出的独立分量，重复此过程，直至再无独立分量被分离出来为止，此时分离过程结束。

2 ICA改进EMD算法的实现

ICA改进EMD算法的流程或基本思想可以概括为：利用频带滤波将待测信号分解成若干个指定频带的窄带信号，对获得的各窄带信号依次进行经典EMD过程，得到相应于各窄带信号的IMFs并写成矩阵形式，最后利用FastICA算法对各窄带信号获得的IMFs矩阵进行分离，得到真正的IMFs。具体实现步骤如下：

(1)对待分析信号进行快速傅里叶变换(Fast Fourier Transform，FFT)，粗略估计信号频率的大致范围，以峰值点频率作为带通滤波的中心频率，使信号通过指定频带的带通滤波，即将原分析信号分解为若干子带信号之和。

(2)对各子带信号分别进行EMD过程，获得IMFs矩阵c(t)；利用FastICA算法分别对各频段组成的IMFs矩阵c(t)进行分离，得到输出矩阵即为真正的IMFs。

设x(t)为待分析信号，经过频带滤波改进EMD 过程后得到n个IMFs和1个趋势项之和，即：

(2)

式中，r(t)为趋势项;ci(t)为第i个IMFi。

将各IMFs组合在一起，表示成一个n维矩阵形式c(t)：

c(t)=[c1(t),c2(t),…,cn(t)]T

(3)

则盲源分离的输入矩阵即为IMFs矩阵c(t)，借助于FastICA算法估计出真正的IMFs。

3 Benchmark 结构识别

为了验证所提出算法的有效性，将该算法应用到LASC-ASCE结构健康监测工作组提供的4层剪切框架Benchmark模型[17]的模态识别中。结构模型如图2所示，结构分析模型如图3所示。

每层在x、y两个方向各布置2个加速度传感器，因此该结构模型共布置16个传感器，由于结构的激励(w1、w2、w3、w4)方向与y方向同向，因此布置在x方向上的传感器获得的响应非常小，故不对x方向的传感器数据进行分析。

图2 Benchmark结构模型

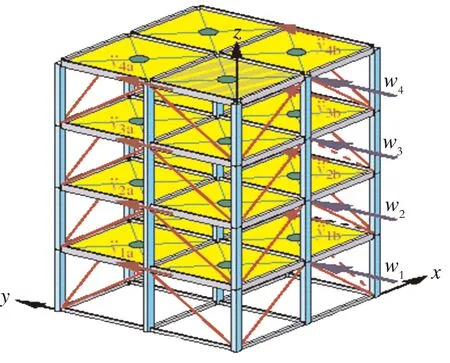
图3 Benchmark结构分析模型

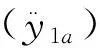
(a) 原始信号及IMFs (b) 频谱

图4经典EMD算法得到的IMFs及其频谱

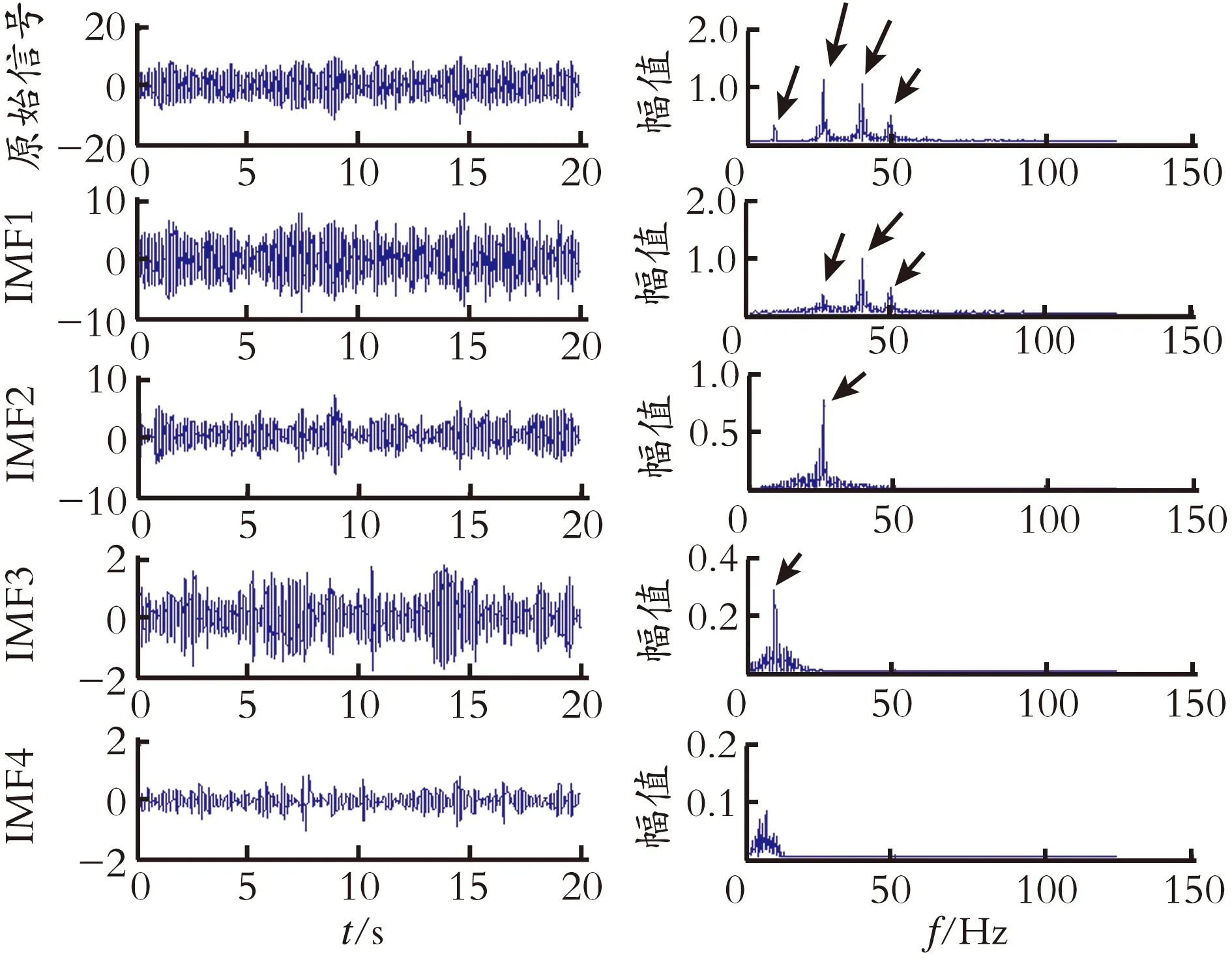
为此，利用所提出的改进EMD算法对该信号进行分析，待分析信号中存在4个明显的频率峰值，选取峰值点的频率值，并以此作为频带滤波的中心频率，构造以各峰值频率为中心频率的带通滤波器，将待分析加速度响应信号分别通过这4个带通滤波器，得到多组IMFs，并利用FastICA算法进行真正IMFs的判别。改进EMD算法加速度响应信号如图5所示。

(a) IMFs (b) 频谱

比较图4和图5可知，利用经典EMD算法得到的各IMF分量的频谱图中所包含的频率组分明显地混叠在一起，严重影响模态频率的识别结果。利用所提出的改进EMD算法得到的频谱图，非常清晰地展示了各IMF组分的频率分布，各频率组分一目了然，均为单一组分，可观性好，即本文所提出的改进算法可以很好地解决经典EMD算法所存在的模态混叠和虚假模态的现象，并实现了真正IMF的自动识别，保证了经过频带滤波和FastICA联合改进EMD算法分解得到的IMF均为单一组分，为后续与HT算法相结合准确识别结构模态参数奠定了基础。

最后分别将利用经典EMD算法和改进EMD算法得到的IMFs与希尔伯特变换(Hilbert Transform, HT)算法[1]相结合，进行结构模态参数的识别，模态频率的识别结果见表1。

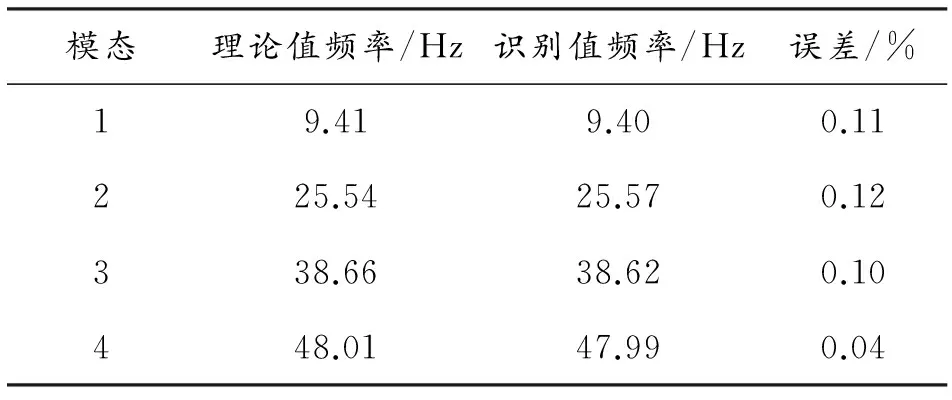
表1 模态频率识别结果

从表1中可以看出，由于改进EMD算法消除了模态混叠的现象和虚假模态，保证获得的每个IMF都含有单一的频率组分，很好地满足了IMF的定义。因此，在后续进行模态参数识别时，得到了很高的识别精度。

4 结 论

针对经典EMD算法中存在的模态混叠现象这一缺陷，提出了基于频带滤波和FastICA改进的EMD算法，并通过Benchmark结构的数值算例验证了所提出的改进EMD算法，有效地避免了经典EMD中的模态混叠和虚假模态现象，保证了所获得的IMF均为单一组分，把EMD算法分解过程中产生的虚假模态看成是噪声，借助于FastICA算法来快速消除虚假模态，并实现了真正IMF的自动判别。最后利用HT算法准确识别出结构的模态频率，相比未改进的经典EMD算法具有明显的优势。因此，所提出的算法用于结构的模态参数识别是可行的，并获得了令人满意的识别结果。

[1] 陈隽，徐幼麟.HHT方法在结构模态参数识别中的应用[J].振动工程学报，2003,16(3):383-387.

[2] 李中付，宋汉文，华宏星,等.基于环境激励的模态参数识别方法综述[J]. 振动工程学报，2000,13(5):578-585.

[3] 黄迪山.经验模态分解中虚假模态分量消除法[J].振动、测试与诊断，2011，31(3)：381-384.

[4] 罗周全,左红艳,吴超,等.基于改进EMD的地下金属矿山围岩声发射信号去噪声处理[J]. 中南大学学报(自然科学版)，2013，44(11):4694-4701.

[5] 张志刚，石晓辉，施全，等.基于改进EMD和谱峭度法滚动轴承故障特征提取[J].振动、测试与诊断，2013，33(3):478-482.

[6] 张志刚,石晓辉,陈哲明,等.基于改进EMD与滑动峰态算法的滚动轴承故障特征提取[J]. 振动与冲击，2012，31(22):80-83.

[7] 李再帏,练松良,周俊磊.基于改进EMD方法的轨道不平顺时频分析[J]. 同济大学学报(自然科学版),2012，40(5):702-706.

[8] 姚刚,赵建军,姚跃亭,等.基于改进EMD方法的系统误差分离方法研究[J]. 振动与冲击，2014，33(14):176-180.

[9] 权友波, 王甲峰, 岳旸, 等. 盲源分离技术现状及发展趋势[J]. 通信技术，2011，44(4):13-15.

[10] Zhou W, Chelidze D. Blind source separation based vibration mode identification[J]. Mechanical Systems and Signal Processing, 2007, 21(8):3072-3087.

[11] Blanco D,Mulgrew B, Ruiz D P, et al. Independent component analysis in signals with multiplicative noise using fourth-order statistics[J]. Signal Processing, 2007, 87(8):1917-1932.

[12] 何沿江,齐明侠,罗红梅.基于ICA和SVM的滚动轴承声发射故障诊断技术[J].振动与冲击，2008，27(3):150-153.

[13] 张建伟,暴振磊,江琦.小波-ICA联合技术在水工结构应变损伤识别中的应用[J]. 振动与冲击,2016，35(11):180-185.

[14] 柏林,陆超,赵鑫.基于ITD与ICA的滚动轴承故障特征提取方法[J]. 振动与冲击,2015，34(14):153-156.

[15] 蔡剑华,胡惟文,王先春.基于EMD-ICA去噪的滚动轴承故障诊断方法[J]. 机械设计,2015，32(1):17-23.

[16] 姜绍飞,陈志刚,沈清华,等.基于EEMD与FastICA的损伤异常识别与定位[J]. 振动与冲击,2016，35(1):203-209.

[17] Johnson E A, Lam H F, Katafygiotis L S, et al. A benchmark problem for structural health monitoring and damage detection[C]// Structural Control for Civil and Infrastructure Engineering, International Workshop on Structural Control. 2001:317-324.

Research on Improved EMD Algorithm Based on FastICA

Fu Chun1， Sun Xianglei1， Wang Kun1， Guan Haiwei1， Liu Juan1， Li Ming2

(1.CollegeofPetroleumEngineering,LiaoningShihuaUniversity,FushunLiaoning113001，China;2.CollegeofCivilEngineering,ShenyangJianzhuUniversity,ShenyangLiaoning110168，China)

The Empirical mode decomposition (EMD) has significant advantages in nonlinear and non-steady response signal processing algorithms, but in the actual application process, the EMD existed some defects, in which the modal aliasing and false mode phenomenon is most prominent, the modal aliasing phenomenon can be simple in the 1 intrinsic mode function (IMF) containing more than one order structure of intrinsic mode components. The false mode phenomenon is the frequency component that should not be existed, which has a serious influence on the identification accuracy of structural modal parameters. To solve this problem, this paper studies the above two defects in EMD, and proposes an improved EMD algorithm which combines the fast ICA algorithm (FastICA) in frequency band filtering and independent component analysis (ICA) algorithm. The structure frequency is identified by hilbert transform (HT), and the effectiveness of the proposed algorithm is verified by the the Benchmark structure.

Empirical mode decomposition (EMD); Blind source separation (BSS); Mode mixing; Hilbert transform (HT)

1672-6952(2017)05-0067-04

投稿网址：http://journal.lnpu.edu.cn

2017-03-19

2017-04-06

住建部科学技术计划项目(2016-K5-009)。

付春(1980-)，女，博士，讲师，从事结构健康监测与损伤识别研究；E-mail：fuchun@lnpu.edu.cn。

TU317+.5；TU311.3

A

10.3969/j.issn.1672-6952.2017.05.013

(编辑 陈 雷)