螺栓法兰系统连接可靠性分析方法
范登帅, 高 鹏, 刘智慧, 徐晶晶, 杨亚南, 吴天航, 袁世娇
(辽宁石油化工大学 机械工程学院,辽宁 抚顺 113001)
螺栓法兰系统连接可靠性分析方法
范登帅, 高 鹏, 刘智慧, 徐晶晶, 杨亚南, 吴天航, 袁世娇
(辽宁石油化工大学 机械工程学院,辽宁 抚顺 113001)
考虑系统内零件间的失效相关机理,提出了螺栓法兰连接系统的动态可靠性和失效率模型,指出了传统静态可靠性模型无法精确描述螺栓法兰系统可靠性和失效率的动态特征,并通过算例分析了失效相关对系统可靠性和失效率的影响。结果表明,失效相关对系统可靠性具有较大影响,零件相互独立假设可能引起系统可靠性分析的较大误差;传统恒定失效率假设可能低估系统可靠度;螺栓数量的增加可以增强系统抵抗失效风险能力。
可靠性; 螺栓; 系统; 失效率; 失效相关
螺栓法兰结构是机械系统中重要的连接与密封结构,在石油化工、航空航天、工程机械等领域应用广泛,其可靠性的正确评价对工程系统的质量评估和安全保障具有重要意义。由于工作载荷的不确定性及零部件材料加工过程中的随机性,传统确定性意义下的机械系统分析方法已经不能满足现代机械设计需求。此外,由于螺栓法兰系统中机械零件间的相互作用以及零部件工作性能的不确定性,螺栓法兰连接结构的系统行为特征呈现出明显的随机特性。因此,有必要对螺栓法兰系统可靠性评价方法进行深入研究。
国内外学者对螺栓法兰系统的连接特征和可靠性分析方法进行了研究[1-9]。T.Sawa等[5-6]在热传导的条件下,研究了管道法兰系统中螺栓与螺母对系统连接行为的影响;使用有限差分法,对连接瞬态热传导的温度分布进行了分析,为管道法兰连接特性分析提供了理论基础;根据轴对称三维弹性理论,对连接接触应力分布以及螺栓连接过程中的最大应力进行了分析。张庆雅等[7]详细分析了法兰旋转和内压作用下法兰系统的应力和变形,从而建立法兰环和螺栓的极限状态方程,计算了螺栓法兰系统可靠性。蔡永梅等[8]采用ANSYS软件,对非标准法兰强度进行分析,获得了工作状态下法兰的应力分布,再通过 Monte Carlo仿真方法提出了法兰系统可靠性计算方法。纪冬梅等[9]考虑垫片、螺栓和法兰参数的随机性,建立可靠性优化目标函数,通过网格寻优方法提出了螺栓法兰系统的优化设计方法。这些研究方法为螺栓法兰系统的可靠性分析提供了有效的理论基础。
本文在现有可靠性分析方法的基础上,从系统层次出发,考虑系统中子部件内部及工作载荷的随机性,建立了系统可靠性评估方法。在所建立的可靠性模型中,考虑了机械系统中广泛存在的失效相关问题,该模型可用于螺栓法兰连接系统的动态可靠性分析,克服了传统静态可靠性设计方法中难以考虑可靠性时变特征的困难,为系统动态可靠性分析理论提供了基础。
1 螺栓法兰系统可靠性模型
传统机械系统可靠性分析主要基于系统结构函数和应力强度干涉模型[10]。应力强度干涉模型是机械零件可靠性分析的重要方法,通过应力与强度两个随机变量的统计特征,计算零件不失效的概率来确定零件可靠度。在螺栓法兰系统中,螺栓是最重要的承力元件,是整个法兰系统中的薄弱环节。因此,本文主要考虑法兰系统中螺栓组的连接可靠性分析方法。由螺栓组连接机理可知,系统逻辑上构成并联系统。根据传统机械系统可靠性计算方法,系统中每个螺栓的可靠度R1可根据应力强度干涉模型获得,其数学表达式为[10]:

(1)
式中,s为螺栓的应力,MPa;r为强度,MPa;fs(s)、fr(r)分别表示螺栓应力s和强度r的概率密度函数。
在确定螺栓的可靠度后,可根据经典可靠性理论,求解n个螺栓所组成并联系统的可靠度R2:

(2)
可靠性的定义明确了其本质上所具有的时变属性。由于载荷强度干涉模型的静态本质,无法考虑零件全寿命周期内的动态变化规律,在实际应用中收到较大限制。此外,传统机械系统可靠性模型中往往假设零件间统计独立,系统可靠度可由零件可靠度和独立系统结构函数获得。但是,如前所述,螺栓在承力过程中具有明显的失效相关特征。因此,这样的独立假设可能带来较大的可靠度计算误差。如果考虑螺栓的疲劳使用寿命,根据s-N曲线理论,其承载应力与使用寿命之间的关系可表示为[11]:
smN=C
(3)
式中,N为确定性应力s下螺栓的平均使用寿命;C、m为材料常数。通常,机械零件的平均寿命与零件失效率呈倒数关系。如果已知某标准应力s0对应的标准失效率λ0,则可求导得出螺栓的动态可靠性模型R3[12]:
(4)
式中,t表示时间。如果考虑螺栓在加工制造过程中所引起的材料性能随机性,并用λ0的概率密度函数f(λ0)来表示这种随机性,考虑螺栓组在连接过程中所承受的共同载荷,系统可靠度R4可表示为:
(5)
系统的失效率δ1可表示为:

(6)
如果假设螺栓统计意义上是相互独立的,则可得独立系统可靠度R5,其表达式为:
(7)
相应的失效率δ2为:
(8)
2 算 例
某螺栓法兰由8个相同螺栓完成连接功能,共同组成如图1所示的并联系统。系统承受共同的随机载荷。每个螺栓上所承受的应力服从均值为0.500 MPa、标准差为0.050 MPa的正态分布,标准载荷s0为0.500 MPa,其所对应的失效率服从均值为0.03 h-1、标准差为0.01 h-1的正态分布,并且m=2。系统可靠度与失效率随时间变化规律分别如图2和图3所示。为了便于对比,独立假设下的系统可靠度和失效率同时示于图2和图3中。在传统机械系统可靠性建模过程中,常认为系统失效率为常数,缺乏随机应力对可靠性动态特性影响的分析。因此,针对该假设,在本算例中将标准载荷s0对应失效率下的可靠度也示于图2中。
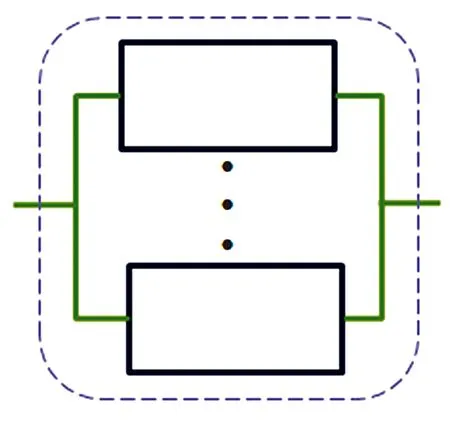
图1 螺栓法兰连接系统可靠性逻辑框图

图2 可靠度随时间的变化规律

图3 系统失效率随时间的变化规律
由图2和图3可知,系统可靠性与失效率均体现出明显的动态特征,传统的静态可靠性模型无法对系统可靠性的时变特性和失效率进行定量评估。在承载共同工作载荷过程中,系统内零件间发生失效相关。如果按照传统独立假设下的系统结构函数进行计算,则会产生较大误差。总体上,失效相关的存在使系统可靠性降低,失效率升高,减弱并联系统冗余结构的安全保障性能。因此,传统的独立假设会使可靠性评估结果偏于危险。同时,恒定失效率假设明显低估系统可靠性评价结果。传统机械系统可靠性设计方法认为,可采用浴盆曲线中偶然失效阶段的恒定失效率数据来计算数据。但是,由于材料性能和载荷随机特性的存在,这样的恒定假设可能带来较大的可靠度计算误差。
在λ0的标准差(标准失效率分散性)分别为0.003、0.006 MPa和0.010 MPa的条件下,相关系统的可靠度和失效率分别如图4和图5所示。为了分析元件个数对系统可靠性的影响,对不同数目元件下的系统可靠度进行了研究,结果如图6所示。

图4 不同标准失效率分散性下系统动态可靠度

图5 不同标准失效率分散性下系统失效率

图6 螺栓数不同时系统的动态可靠度
由图4和图5可知,标准失效率分散性对系统可靠性与失效率有较大影响,表明不同螺栓使用寿命分散性条件下,系统可靠性和失效率评估结果会有较大不同,分散性增大会降低系统的失效速度。
由图6可知,随着螺栓数量的增加,系统承担失效风险的能力得到加强,但同时也增加设计成本和结构复杂度,在机械优化设计中要综合考虑这些因素对结构设计的影响。
3 结 论
本文提出了螺栓法兰连接系统的动态可靠性和失效率计算方法。在所提出的可靠性模型中,考虑系统内零件间的失效相关机理,分析了失效相关对系统可靠性和失效率的影响。结果表明,传统静态可靠性模型无法精确反映螺栓法兰系统连接可靠性和失效率随时间的变化规律;传统恒定失效率假设可能低估系统可靠度;螺栓数量的增加可以增强系统的抗失效风险能力;失效相关对系统可靠性具有较大影响,零件相互独立假设可能引起系统可靠性分析的较大误差。本文提出的模型还可用于分析螺栓使用寿命分散性对系统可靠性和失效率的影响。
[1] Engelhardt M D,Husain A S.Cyclic-loading performance of welded flange-bolted web connections[J].Journal of Structural Engineering,1993,119(12): 3537-3550.
[2] Ito Y,Toyoda J,Nagata S.Interface pressure distribution in a bolt-flange assembly[J].Journal of Mechanical Design, 1979,101(2): 330-337.
[3] Kim T,Whittaker A S,Gilani A S J,et al.Cover-plate and flange-plate steel moment-resisting connections[J]. Journal of Structural Engineering,2002,128(4):474-482.
[4] Gotoh M,Ishise F.A finite element analysis of rigid-plastic deformation of the flange in a deep-drawing process based on a fourth-degree yield function[J].International Journal of Mechanical Sciences,1978,20(7):423-435.
[5] Sawa T,Hirose T,Kumano H.Behavior of pipe flange connection in transient temperature field[J].Journal of Pressure Vessel Technology,1993,115(2):142-146.
[6] Sawa T,Higurashi N,Akagawa H.A stress analysis of pipe flange connections[J].Journal of Pressure Vessel Technology,1991,113(4):497-503.
[7] 张庆雅,汪亮.垫片螺栓法兰连接系统的强度可靠性分析[J].机械科学与技术,2003, 22(S1):79-83.
[8] 蔡永梅,张瑞革,谢禹钧.非标准法兰的有限元分析及可靠性设计[J].石油化工设备,2008,37(2):32-35.
[9] 纪冬梅,周昌玉.整体法兰可靠性优化设计[J].南京工业大学学报,2002,24(3):78-81.
[10] Xue J,Yang K.Upper and lower bounds of stress-strength interference reliability with random strength-degradation[J].IEEE Transactions on Reliability,1997,46(1):142-145.
[11] Lotsberg I,Sigurdsson G.Hot spot stress SN curve for fatigue analysis of plated structures[J].Journal of Offshore Mechanics and Arctic Engineering,2006,128(4):330-336.
[12] 高鹏,谢里阳.机械零件可靠度估算方法[J].机械设计,2011,28(2):90-93.
A Method of Connection Reliability Analysis of Bolted Flange Systems
Fan Dengshuai, Gao Peng, Liu Zhihui, Xu Jingjing, Yang Ya,nan, Wu Tianhang, Yuan Shijiao
(SchoolofMechanicalEngineering,LiaoningShihuaUniversity,FushunLiaoning113001,China)
Dynamic reliability models and failure rate models of bolted flange systems were developed, which took into account the failure dependence of components in the systems. It was proposed that the traditional static reliability models could not accurately describe the dynamic characteristics of reliability and failure rate of bolted flange systems. Moreover, the effects of failure dependence on system reliability and failure rate were analyzed via numerical examples. The results showed that the failure dependence had great influences on system reliability. Furthermore, the assumption that components in a system were independent of each other might cause large error in system reliability estimation. Traditional assumption of constant failure rate for mechanical systems might underestimate the system reliability. The increase in the number of bolts could enhance the ability of the system to resist the risk of failure.
Reliability; Bolt; System; Failure rate; Failure dependence
1672-6952(2017)05-0049-04
投稿网址:http://journal.lnpu.edu.cn
2016-09-09
2017-02-27
国家自然科学基金项目(51505207);辽宁省教育厅科学研究一般项目(L2015298);辽宁省自然科学基金资助项目(2015020152);辽宁省大学生创新创业项目(201510148053)。
范登帅(1995-),男,本科生,化工机械设计专业,从事机械系统可靠性方面的研究;E-mail:893048846@qq.com。
高鹏(1982-),男,博士,副教授,从事机械系统可靠性和机械动力学方面的研究;E-mail:gaogaopeng@163.com。
TH122;TB114.3
A
10.3969/j.issn.1672-6952.2017.05.010
(编辑 宋锦玉)

