On the properties of generalized fibonacci numbers with binomial coefficients
ZHANG Caihuan, LIU Dong
(1.Department of Mathematics, Luoyang Normal University, Luoyang, Henan, 471022 ;2.Department of Information Technology, Luoyang Normal University, Luoyang, Henan 471022)
Onthepropertiesofgeneralizedfibonaccinumberswithbinomialcoefficients
ZHANG Caihuan1*, LIU Dong2
(1.Department of Mathematics, Luoyang Normal University, Luoyang, Henan, 471022 ;2.Department of Information Technology, Luoyang Normal University, Luoyang, Henan 471022)
In this paper, we obtained many new important properties by studying generalized Fibonacci numbers and summarized some properties of generalized Fibonacci numbers by binomial coefficients.
binomial coefficient; generalized Fibonacci numbers; binomial expansion
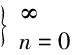
Fn+1=Fn+Fn-1,F0=0,F1=1;
(1)
un+1=pun+un-1,u0=0,u1=1.
(2)
Fnandunare called thenth Fibonacci number and generalized Fibonacci number respectively. These numbers are well-known for possessing wonderful and amazing properties (consult [1] together with their very extensive annotated bibliography for additional references and history) Moreover, for thenth Fibonacci number, it is well known that the sum of the squares is
Also, the elegant formula is
Recently, there has been a huge interest of the application for Fibonacci and Lucas numbers in all sciences. For the pretty and rich applications of these numbers and their relatives one can see science and the nature [2-10]. There are many different generalizations in the theory of Fibonacci numbers, among other generalizations in the distance sense, and there are many types of identities containing sums of certain functions of binomial coefficients and Fibonacci or Lucas numbers. All of these are special cases of the following two identities.

In [11], the author gave some properties of Fibonacci numbers with binomial coefficients. Motivated by it, in this paper, we concentrate on the generalized Fibonacci numbers and show some interesting results.
1 Main results
For the generalized Fibonacci {un} defined in (2), we know:
u0=0,u1=1,u2=p,u3=p2+1,
u4=p3+2p,u5=p4+3p2+1,
u6=p5+4p3+3p,…
Generally, we have the following result:
Theorem1Forn∈Z+,
un+6=p(p2+3)un+3+un.
(3)
ProofWe use the principle of mathematical induction onn. Forn=1,
u7=p(p2+3)u4+u1=
p(p2+3)(p3+2p)=p6+5p4+6p2+1.
And from the equation (2), we have
u7=pu6+u5=
p(p5+4p3+3p)+p4+3p2+1=
p6+5p4+6p2+1.
Assume that it is true for all positive integersn=k. That is
uk+6=p(p2+3)uk+3+uk.
(4)
We need to show that it is true forn=k+1. That is
u(k+1)+6=p(p2+3)u(k+1)+3+u(k+1).
(5)
The right hand side of equation (5) can be written as
p(p2+3)u(k+1)+3+u(k+1)=
p(p2+3)uk+4+u(k+1)=
p(p2+3)(puk+3+uk+2)+puk+uk-1=
p(p(p2+3)uk+3+uk)+
(p(p2+3)uk+2+uk-1).
From (4), we know
p(p2+3)uk+3+uk=uk+6
and
p(p2+3)uk+2+uk-1=uk+5,
so we have
p(p2+3)u(k+1)+3+u(k+1)=
p(p2+3)uk+4+u(k+1)=
puk+6+uk+5=uk+7=u(k+1)+6.
Thus (5) is true. Therefore, the result is true for everyn>0.
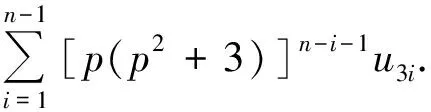
(6)
u9=p(p2+3)u6+u3=
p(p2+3)×p(p2+3)(p2+1)+u3=
(p2+1)[p(p2+3)]2+u3.
ProofWe use the principle of mathematical induction onn. Forn=2, by Theorem 1,the identity (6) is true. Assume that it is true forn=m-1≥3. That is
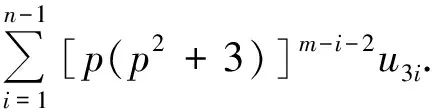
(7)
We need to show that it is true forn=m. Then by Theorem 1, we have
u3m+3=u3(m-1)+6=
p(p2+3)u3(m-1)+3+u3(m-1)=
p(p2+3)u3m+u3(m-1),
and by assumption, we know
u3m+3=p(p2+3)((p2+1)[p(p2+3)]m-1+
(p2+1)[p(p2+3)]m+
Equation (6) is true forn=m.
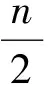
(8)
For this theorem, we will give two proves of it. The first is perceptual intuition, and the second we will use the principle of mathematical induction.
⋮

It is clear that the multipliersa,ab2,ab4, …,abnofu3,u9,u15, …,ukhave the binomial coefficients as:
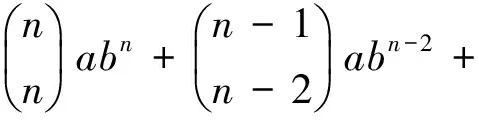
or briefly, we write
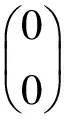
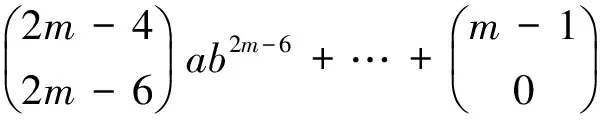
(9)
We need to show that it is true forn=2m. Thenk=6m+3x, by Theorem 1, we have
u6m+3=u6(m-1)+3+6=
p(p2+3)u6(m-1)+3+3+u6(m-1)+3=
bu6m+u6m-3=u6m-3+bu6(m-1)+6=
u6m-3+b(bu6(m-1)+3+u6(m-1))=
u6m-3+b2u6m-3+bu6(m-2)+6=
u6m-3+b2u6m-3+b(bu6(m-2)+3+u6(m-2))=
…=
u6m-3+b2u6m-3+b2u6m-9+b2u6m-15+…+b2u3.
(10)
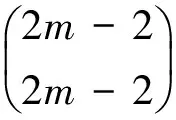
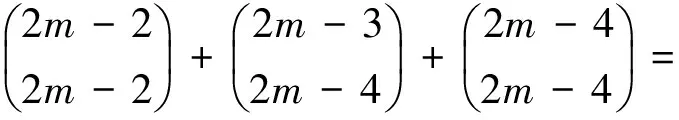
And so on, we have the identity
And so the equation (8) is true forn=2m, then we complete the proof.
By the same method, we can obtain the following theorem:
ProofThe proof of this theorem is similar to the proof of Theorem 3, so we omitted it.
2 Applications
By Theorem 1~4, we could have the following results, and the proves were left to interested readers.
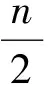
Corollary2Forn∈,-1=nandn≥0,
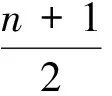
Corollary4Forn∈,-1=nandn≥0,
[1] KALMAN D, MENA R. The Fibonacci numbers exposed [J]. Math Mag, 2003,76(3): 167-181.
[2] KILIC E. Sums of generalized Fibonacci numbers by matrix methods [J]. Ars Combinatoria, 2007,84(84):23-31.
[3] KOSHY T. Fibonacci and Lucas Numbers with Applications [M]. NY: John Wiley and Sons, 2001.
[4] STAKHOV A. Fibonacci matrices, a generalization of the 'Cassini formula’ and a new coding theory Chaos[J]. Solitons & Fractals, 2006,30(1):56-66.
[5] ZhANG C H. On the generalized Fibonacci matrix of order 2Γ(k) Sequence {FΓ(2k)n}[J]. Ars Combinatoria, 2001,59:7-14.
[6] FALCON S, PLAZA A. The k-Fibonacci sequence and the Pascal 2-triangle[J]. Chaos Soliton Fract, 2007,33(1):38-49.
[7] FARROKHI D G M. Some remarks on the equationFn=kFmin Fibonacci numbers[J]. J Integer Seq, 2007,10(5):1-5.
[8] SPIVEY M Z. Combinatorial sums and finite differences[J]. Discrete Math, 2007,307(24):3130-3146.
[9] AKBULAK M, BOZIKURT D. On the order-m generalized Fibonaccik-numbers [J]. Chaos Soliton Fract, 2009,42(3): 1347-1355.
[10] DEMIR A, OMUR N, ULUTAS Y T. Parametrized Fibonacci search method withk-Lucas numbers[J]. Appl Math Comput, 2008,198(1):355-360.
[11] GULEC H H, TASKARA N. On the properties of Fibonacci numbers with binomial coefficients[J]. Int J Contemp Math Sciences, 2009,4(25):1251-1256.
带有二项式系数的广义数Fibonacci的相关性质
张彩环1, 刘 栋2
(1.洛阳师范学院 数学科学学院, 河南 洛阳 471022; 2.洛阳师范学院 信息技术学院, 河南 洛阳 471022)
该文通过研究广义的Fibonacci数,得到了许多重要的性质,并且,用二项式系数对广义Fibonacci数的一些性质进行了概括.
二项式系数; 广义的Fibonacci数; 二项展开
O157.1
A
2017-03-24.
the National Natural Science Foundation of China (11371184).
1000-1190(2017)05-0581-04
*E-mail: zhcaihuan@163.com.
10.19603/j.cnki.1000-1190.2017.05.004

