1993~2015年中国南海海平面变化的初步研究
潘 轶,岳建平,宋亚宏,彭刚跃,章 鹏
(1.河海大学地球科学与工程学院,江苏 南京 211100)
1993~2015年中国南海海平面变化的初步研究
潘 轶1,岳建平1,宋亚宏1,彭刚跃1,章 鹏1
(1.河海大学地球科学与工程学院,江苏 南京 211100)

利用多代卫星测高资料,采用线性回归、傅里叶变换、经验模态分解(EMD)算法等,对1993~2015年中国南海海平面变化的规律进行分析。结果表明,近23 a来,中国南海海平面总体呈现明显上升趋势,平均上升速率为 2.4 mm/a,具体上升速率呈现先上升后下降趋势。中国南海海平面存在显著的年际和年代际变化,其主要变化周期有1 a,0.5 a,1.5 a,2~3 a,4~7 a,其中最显著的为1 a周期信号,夏秋季节海平面高度较高,春冬季节较低。
卫星测高;南海海平面变化;线性回归;傅里叶变换;EMD算法
海平面变化对人类生存环境有着重大影响,海平面变化的规律研究及科学预测同时具有理论和现实意义。目前,直接获取海面高数据的方法主要有验潮站、卫星测高等[1]。验潮站法测海面高有一定的局限性,它只包括少部分设有验潮站的分散地点数据,不具有完整性;其次,这些地点的数据受板块运动的影响,存在不确定性,对历史记录的质量也不好把握[2]。随着卫星测高技术的出现,一种能够获取大空间跨度、大时间跨度、高质量的海面高数据的方法诞生了。
很多学者对全球海平面变化进行过深入研究,但对区域海平面变化规律的研究还不够广泛。南海是半开放式的海洋,被中国大陆、中国台湾及越南、马来西亚、印度尼西亚包围。它属于太平洋边缘海,通过台湾海峡、吕宋海峡和马六甲海峡连接东海、太平洋和印度洋[3]。李立[4]等利用 T/P 测高卫星资料得到1993~1999年南海平均海平面变化趋势为10 mm/a,其中吕宋海峡西部上升速率最大,为 27 mm/a。Cheng和Qi[5]进一步分析了1992年10月~2006年1月的南海卫星测高数据,发现1993~2000年南海海平面平均上升速率为 11.3 mm/a,2001~2005 年下降速率为 11.8 mm/a。本文利用多代卫星测高资料,探讨了1993~2015年中国南海海平面变化的规律。
1 数据与方法
1.1 数据
采用的数据为法国AVISO提供的网格化海平面距平(MSLA)数据,时间跨度为1993-01~2015-12,空间跨度为 105~125°E、5~25°N。该数据融合了 T/P、Jason-1、Jason-2、ERS和ENVISAT等多代卫星测高资料,是研究海平面变化精度最高、完整性最好的数据源。本文采用该数据为原始数据,获取1993-01~2015-12南海每月海平面异常的平均值,得到近23 a来南海海平面变化的时域波形。
1.2 方法
1.2.1 线性回归
线性回归[6]是利用最小二乘法对一个或多个自变量与因变量之间的关系进行建模的一种回归分析。本文采用线性回归方法研究时间与南海海平面异常的关系,求出近23 a来南海海平面变化的线性趋势及上升速率。
1.2.2 傅里叶变换
傅里叶分析方法[7]是信号分析中一种最基本的方法,它将信号从时间域变换到频率域,方便研究信号的频谱规律。离散信号x(n)的傅立叶变换定义如下:
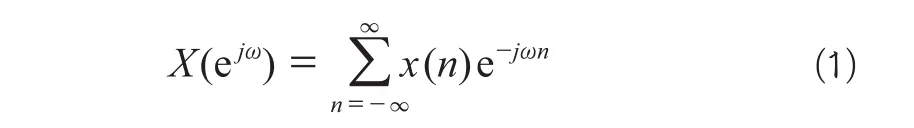
式中,ω为角频率,与普通频率f和采样频率fs的关系为:

通过离散傅立叶变换,时域信号x(n)转化为频域信号X(ejw),即频谱,反映了信号的频域分布及变化规律。
本文对获取的1993~2015年南海月平均海平面异常值变化的时域波形进行傅里叶变换,得到频谱分析图,以便于分析南海海平面变化的变化频率,即周期信号。
1.2.3 经验模态分解方法(EMD)
经验模态分解方法[8,9]的核心思想在于,将时间序列按一定规则分解成有限个本征模函数(IMF)和一个趋势项的和:

本征模函数满足两个条件:①整个过程中信号极值点个数与穿过零点的个数相等或仅差一个;②信号关于时间轴局部对称。实现EMD方法的具体步骤如下:
①对于给定信号x(t),确定所有极值点。将所有极大值点使用3次样条曲线连接形成上包络线,连接所有极小值点形成下包络线。信号x(t)与上下包络线的均值m1之差为:

将h1视作新的x(t),重复式(4),直到h1满足IMF应满足的两个条件,第一阶IMF诞生。
②将h1从x(t)中分离出来,得到:

将r1视为新的x(t),重复步骤①,直到残量rn成为单调函数,不能再继续筛分出IMF:

③数学上,x(t)可表示为:
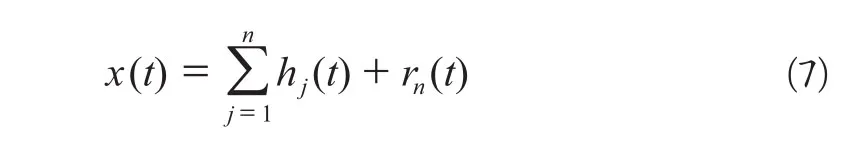
式中,rn(t)为第n阶的残余信号,代表信号中的本征趋势,而各IMF分量hj(t)则代表筛分出的多个信号成分,其频率由高至低、有所不同。同一模态分量中不同时刻处的瞬时频率值也是不同的,其分布随信号本身的变化而变化。
2 结果与讨论
本文利用多代卫星测高资料提供的1993~2015年南海海平面异常数据,选取 105~125°E、5~25°N,计算出23 a来南海海平面变化的时域波形,如图1所示。
由图1明显可得,23 a来中国南海海平面高度变化显著存在1 a的周期信号,夏秋季节海平面高度较高,春冬季节较低。由年平均数据可得,23 a间南海海平面呈“上升-下降-上升-下降”循环变化趋势,总体呈上升趋势。对图1中南海海平面变化时域波形利用傅立叶变换方法作频谱分析,结果如图2所示,中国南海海平面变化的主要周期信号有1 a、0.5 a等。

图1 1993年~2015年由卫星高度计观测的中国南海平均海平面变化(图中蓝色曲线由月平均数据可得,绿色曲线由年平均数据可得)
利用经验模态分解方法进一步分析,对1993~2015年由卫星高度计观测的中国南海平均海平面变化的时间序列进行EMD分解,如图3所示。
分解得到的第一个分量IMF1是高频信号,反映信号的高频变化;第二个分量IMF2是年循环信号;IMF3、IMF4、IMF5、IMF6都为年际震荡,各个分量的频率由高至低变化。最后的一个分量趋势项是1993~2015年中国南海海平面的本征趋势,为单调递增函数。对前5个模态分量进行频谱分析,如图4所示。
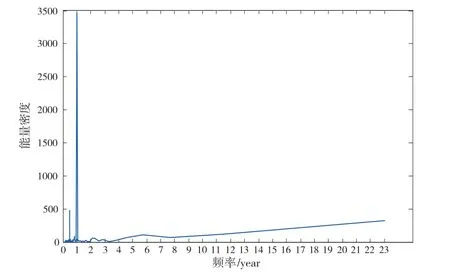
图2 谱分析结果
从图4可以看出,IMF1描述的周期信号为0.5 a,属于高频信号;IMF2描述的周期信号为1 a,其能量密度明显高于其他,代表1 a的周期信号十分显著;IMF3描述的周期信号为1.5 a;IMF4描述的周期信号为 2~3 a;IMF5描述的周期信号为4~7 a。
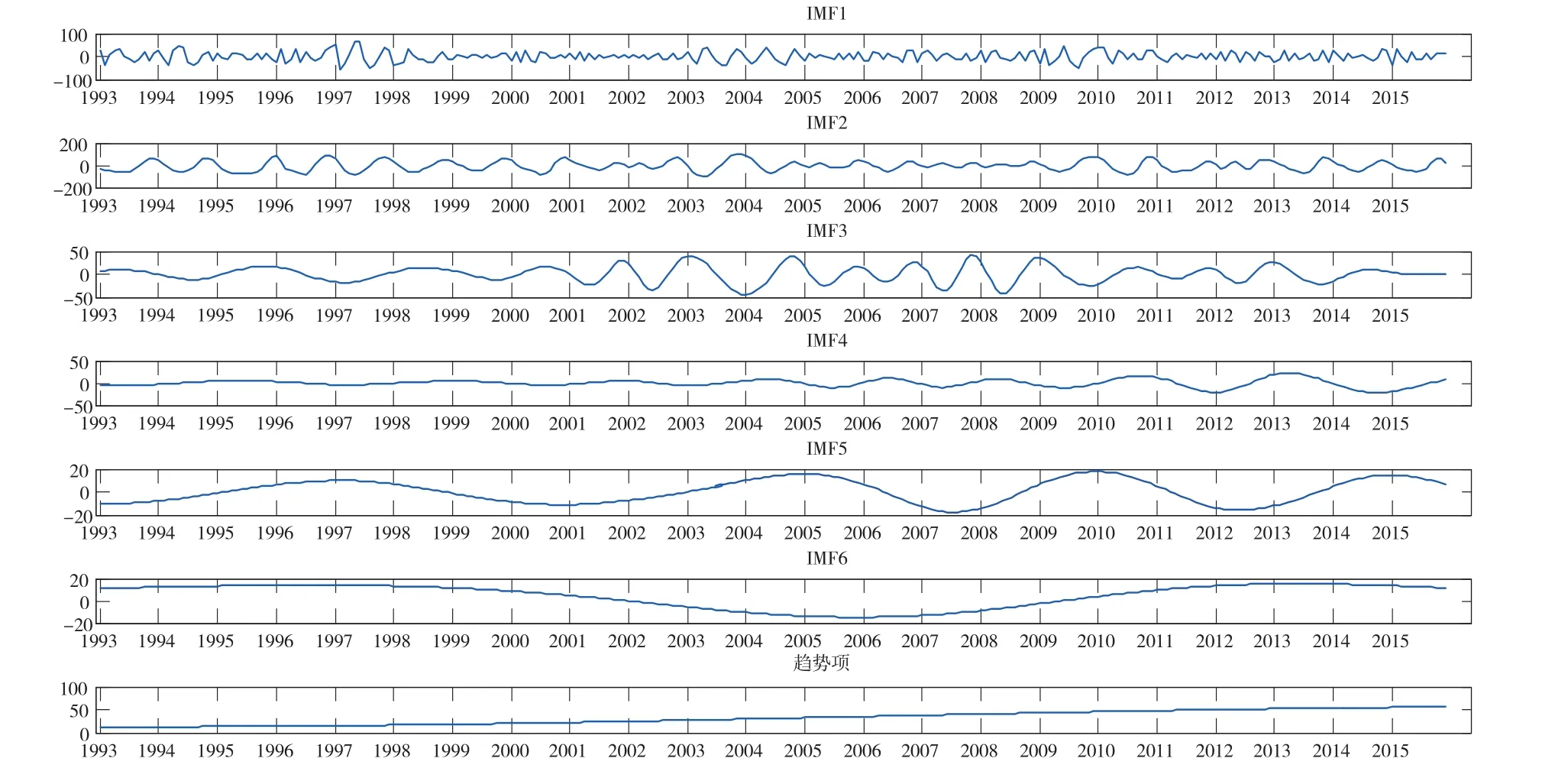
图3 1993 ~2015年由卫星高度计观测的中国南海平均海平面异常的经验模态分解
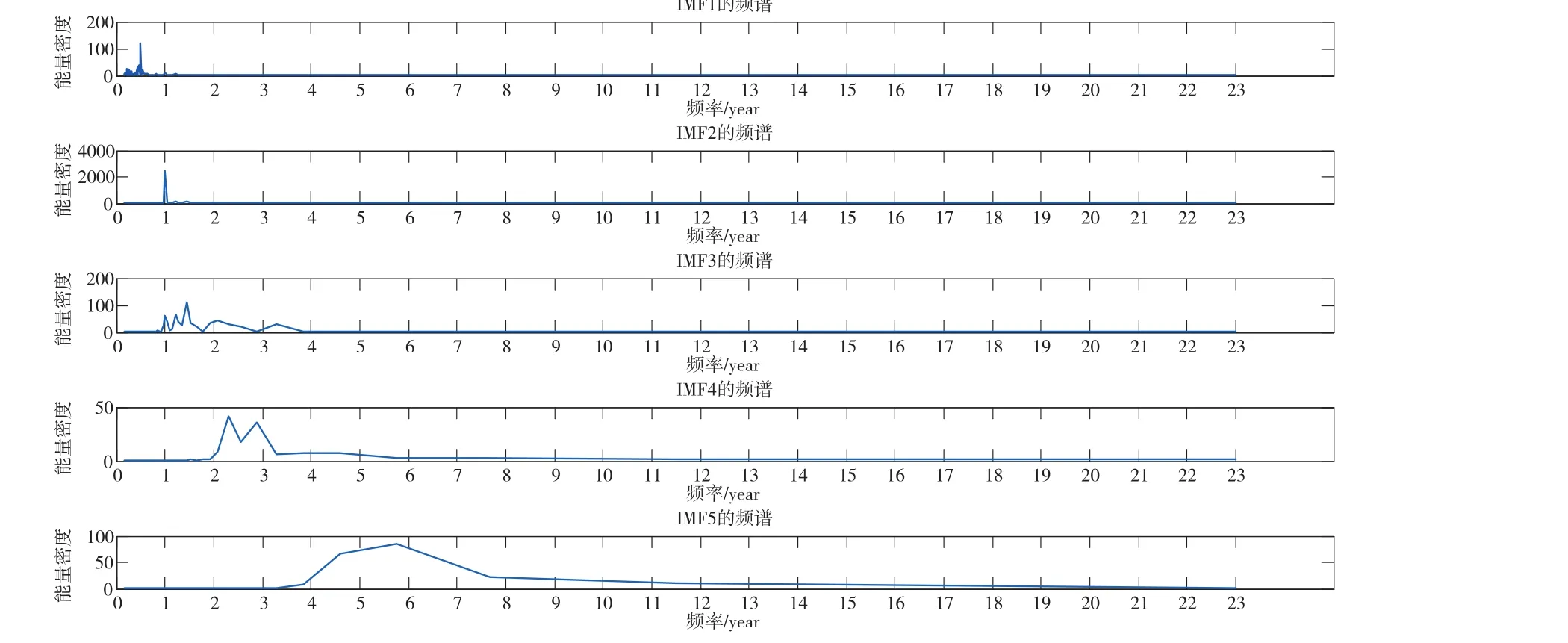
图4 前5个模态分量的频谱分析
对最后一个趋势项进行分析。首先,使用原始数据计算得到1993~2015年各年南海海平面异常高度值,再采用线性回归方法对其进行线性拟合,得到线性趋势图;与EMD分解获得的本征趋势相比较,如图5所示。
由图5中的线性趋势图可得,卫星高度计数据得出的中国南海平均海平面在1993~2015年呈上升趋势,上升速率为2.4 mm/a。由图5中线性趋势与本征趋势的对比可得,EMD方法分解得到的本征趋势是非线性趋势,随着时间的变化而变化,与线性趋势的区别不大,如图6所示。
由图6可得,本征趋势与线性趋势的上升速率曲线有着很大差别。海平面上升的线性趋势是23 a来中国南海海平面变化的平均变化过程只有一个固定值,而本征趋势是瞬时变化的结果,随时间的变化而变化。EMD方法分解所得的本征趋势体现的上升速率经历了一个先上升后下降的变化过程,更细致地反映了23 a间中国南海海平面变化的变化过程。
3 结 语
本文采用融合 T/P、Jason-1、Jason-2、ERS和ENVISAT等多代卫星测高资料的海面高数据建立了统一的海平面变化时间序列,采用线性回归、傅里叶变换、经验模态分解算法等多种方法,研究了1993-01~2015-12期间中国南海平均海平面变化。分析表明,近23 a来,中国南海海平面总体上升,平均上升速率为 2.4 mm/a;具体上升速率随时间变化而变化,呈现先上升后下降趋势;中国南海海平面存在显著的年际和年代际变化,其主要变化周期有 1a,0.5 a,1.5 a,2~3 a,4~7 a;其中,最显著的为1 a周期信号,南海海平面夏秋季节海平面高度较高,春冬季节较低;第二显著的为0.5 a周期信号。

图5 由卫星高度计数据得出的中国南海平均海平面在1993~2015年上升的线性趋势与本征趋势的对比

图6 线性趋势与本征趋势上升速率的对比
[1] 崔树红,谢志仁,钟鹤翔,等.利用T/P海面高度数据校验验潮站地面升降的初步研究[J].地球科学进展,2005,20(6):643-648
[2] Fu Lee-Lueng, Cazenave A. Satellite Altimetry and Earth Sciences [M].London: Academic Press, 2001
[3] 冯伟,钟敏,许厚泽.联合卫星重力、卫星测高和海洋资料研究中国南海海平面变化[J].中国科学,2012,42(3):313-319
[4] 李立,许金电,蔡榕硕.20世纪90年代南海海平面的上升趋势:卫星高度计观测结果[J].科学通报,2002,47(1):59-62
[5] Cheng X H, Qi Y Q. Trends of Sea Level Variations in the South China Sea from Merged Altimetry Data[J]. Global and Planet Change, 2007, 57(1): 371-382
[6] 约翰内特,威廉沃尔曼,迈克尔H库特纳.应用线性回归模型[M].北京:中国统计出版社,1990
[7] 乔新,陈戈.基于11 a高度计数据的中国海海平面变化初步研究[J].海洋科学,2008,32(1):60-64
[8] 顾小丽,李培良,谭海涛.基于RBF神经网络的EMD方法在海平面分析中的应用[J].海洋与湖沼,2009,45(5):532-539
[9] 冯颖.经验模态分解方法在卫星测高数据中的应用[D].青岛:国家海洋局第一海洋研究所,2011
P229
B
1672-4623(2017)10-0009-04
10.3969/j.issn.1672-4623.2017.10.003
2016-08-25。
项目来源:国家自然科学基金资助项目(41174002)。
潘轶,硕士研究生,研究方向为卫星大地测量。

