基于数字控制Buck电路的DC-DC电源变换器仿真研究
孔维功,李丽荣,贾耀华
(1.邢台职业技术学院电气工程系,河北 邢台 054035;2.国网河北大名县供电公司,河北 邯郸 056900)
基于数字控制Buck电路的DC-DC电源变换器仿真研究
孔维功1,李丽荣1,贾耀华2
(1.邢台职业技术学院电气工程系,河北 邢台 054035;2.国网河北大名县供电公司,河北 邯郸 056900)
数字控制DC-DC变换器在低到中功率中的应用可行性在不断提高。基于数字控制Buck电路,提出了一种输入直流电压30~60 V,输出直流电压24 V电源变换器电路,并通过软件仿真验证了所设计数控Buck电路的可行性。在提出DC-DC电源变换器的过程中,采用状态空间平均法进行建模,并且引入S域电压反馈控制回路、添加PID补偿器,实现了稳定有效的DC-DC电源转换。研究结果可为DC-DC变换电路的设计和优化提供一定思路。
数控Buck变换器;状态空间平均法;数字PID补偿器;DC-DC变换
开关电源可以使电源的形式进行互相变化,其由半导体功率器件组成,作为开关它很好地利用了闭环控制对电压输出特性进行调节[1]。DCDC电源转换器属于开关电源一种,其在具备省电要求的紧凑型电子设备和电池供电设备中的应用较为常见。DC-DC电源转换器在良好情况下有高达95%的转换效率。较高的转换效率可以进一步使设备体积减小,也可以大大增加电池周期和寿命。然而目前DC-DC电源转换器系统效率仍然受到自身器件损耗的限制,且明显受到自身工作状态和电源特性的影响,因此如果能够通过合理地设计电源参数而改善转换效率,则具有重要的意义。
1976年,学者R.D.Middlebrook和Slobodan Cuk提出了能够较好地解决PWM型DC-DC变换器的稳态和动态低频小信号分析问题的状态空间平均法[2]。20世纪80年代,美国学者提出使用双向Buck/Boost直流变换器来取代原有的充放电器,以实现汇流电压的稳定[3]。20世纪80年代,PWM型DC-DC开关变换器的闭环控制取得了电压前馈控制和电流程控控制2个重要的进步[4]。1994年,香港大学陈清泉教授(C.C.Chan)进行了电动车用双向DC-DC变换器的研究实验。同年,F.Caricchi教授提出了Buck/Boost级联型双向直流变换器,主要克服了双向直流变换器因输出输入极性相反而不适合于电动车的问题。1998年,美国弗吉尼亚大学的李择元教授开展用与燃料电池配套的双向直流变换器来进行研究和试验工作[3]。
在额外元理论(extra element theorem)[5]的基础上,Jang 和Erickson[6]采用了规范模型(canonical model)和精确的平均模型(average model)[7]推导出了新的输入滤波器的设计标准,也确定了转换器的传递函数。在PCM型控制的转换器中,Ridley[8]和 Middlebrook[9-10]应用了小信号传递函数。Bryant和 Kazimierczuk[11-12]也给出了用 PCM型控制的升压转换器传递函数的框图。
现在DC-DC变换器主要分为以下几种类型:Cuk,Sepic,Zeta双向直流变换器,Buck,Boost,Buck/Boost。隔离式双向DC-DC变换器主要有:正激、反激、推免和桥式等拓扑结构。然而,在所有结构中,Buck是较基本的电路。本文基于数字控制Buck变换器的基本工作模型,计算得到其主电路的器件参数,并通过建立相应的反馈、补偿电路模型对参数进行优化,得到了稳定的直流DC-DC电源转换器,使其能输出适当的电压、电流,达到为电力器件提供稳定低压电源的目的。研究结果可为DC-DC电源转换的设计和优化提供一定参考。
1 数控Buck变换器的建模
1.1 数字控制Buck变换器工作模型
数字控制Buck变换器的基本结构框图如图1所示。

图1 数字控制Buck变换器结构框图Fig.1 The structure block diagram of the digital control Buck converter
图1 工作原理如下:先将输出电压与参考电压的值做差得到误差信号,通过模数转换器采样误差信号,在数字PID补偿器中输入量化后的误差信号e,通过补偿来得到数字信号d,该信号与占空比信号相关,继而进行DPWM模块调制,得到占空比信号,达到控制开关的目的。
数字控制DC-DC变换器和基于Buck电路的DC-DC控制器相比,两者具有相同的基本结构,而反馈控制电路的结构和特性有较大差异。在数控DC-DC变换器中,反馈回路由ADC采样、PID补偿器和DPWM模块组成。这些模块都可以通过在单片机、DSP或FPGA来编写程序。由此可见,数字控制比模拟控制在控制策略灵活度上更具优势。
1.2 参数计算
本文对电路中的参数计算建模做出如下假设来简化计算分析:开关器件和电容电感均视为理想元件;忽略输出电压中的纹波电压值,因为其占空比很小。定义输入的直流电压幅值为UD,平均输出电压值为uo,电压纹波的峰-峰值为ΔUo,输出功率大小为Po,且设开关的导通时间为ton,其与开关周期Ts占空比为D。高频开关电源(也称为开关型整流器SMR)通过MOSFET或IGBT的高频工作,开关频率一般控制在50~100 kHz范围内,实现高效率和小型化增加开关电源频率,因频率的上升而带来开关管、变压器和电压的损耗。本文开关频率设为50 kHz。由于稳态时电感端电压信号呈稳定的周期性变化,认为其在1个周期内对时间积分值为0,根据能量守恒定律,可以推导得出连续及非连续临界条件下的电容值、电感值、纹波电压值以及占空比的计算方法如下式:

本文提出的电源变换器电路要求是将电动车电瓶作为电压输入,将稳定的低压电源提供给电动车内部其他器件,主要指标能够达到下述要求:在输入直流电压30~60 V的电压区间能实现直流24 V的输出,最大输出电流值为10 A,且要求转换效率大于95%。按照该指标要求设计并计算,可得如下结果:
1)由式(1)得到临界电感值:

当L>LC时,电感电流才能处于连续导电模式,因此,电感值可略大于2倍于临界电感值,即为L=0.5 mH。
2)根据纹波要求与式(3)可计算得电容值:
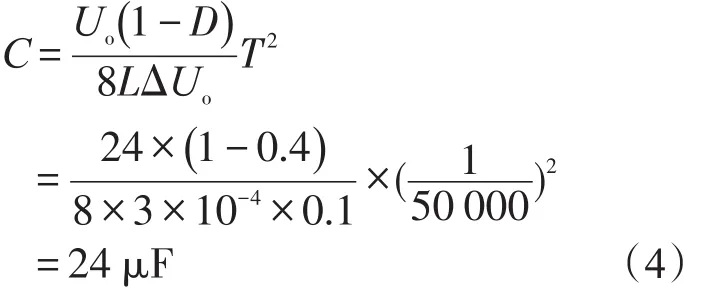
为了使输出纹波更小,可取10倍左右的临界电容,即C=0.2 mF。
2 Buck电路功率级信号模型建立
在分析电路时,由于开关管给整个系统带来非线性因素,所以本文使用状态空间平均法进行建模。状态空间平均法具体方法为:把Buck电路开关的周期按段分配,当工作在连续导电的模式下时开关周期为ton和toff两段部分,如图2所示;如果工作在断续导电模式时,将开关周期分为ton,toff1和toff2这3部分。根据不同的工作模式对Buck电路中的储能元件(电感L,电容C)写出状态方程。加权平均所得到的状态方程组后得到新的状态方程组,利用该方程组为高频开关动作和低频率元件的加权平均进行等效性描述。
当开关闭合时,电压得以输入并且使得电感L开始储能,对输出电容C进行充电保证负载的持续输出,如图2a所示;打开开关时断开了电感和输入电压,在某个周期结束之前靠电感和输出电容向负载提供能量,如图2b所示。
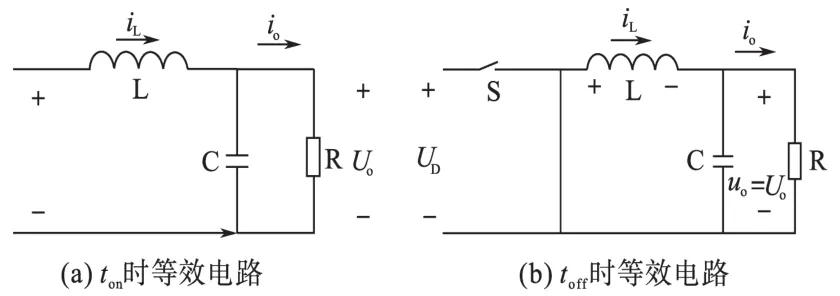
图2 Buck变换电器的两种工作状态Fig.2 The two working statements of Buck converter
由图2可以推得传递函数:
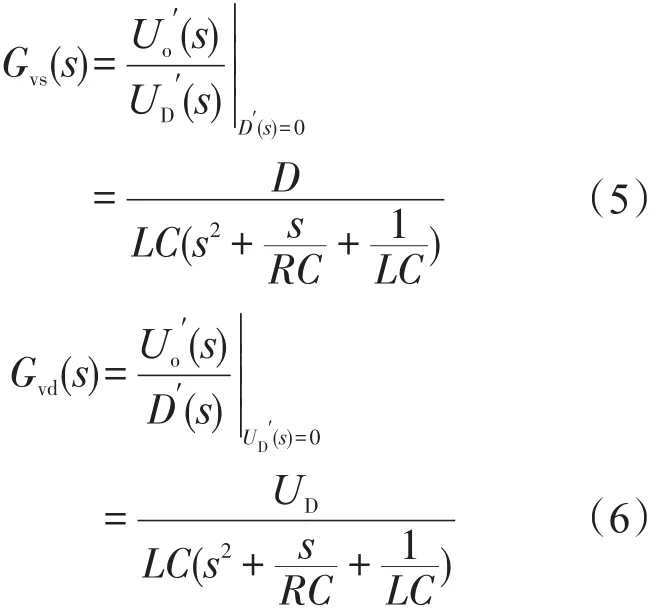
式(5)为Buck电路从控制到输出的函数模型,式(6)为Buck电路从输出至输入的函数模型,即功率级函数模型。将参数代入式(6)可得:

本文选取输入电压为30~60 V来分析。在实际电路的设计中,由于稳定裕量间接地反映系统动态过程的平稳性,稳定裕量大则意味着阶跃响应的超调量小,“阻尼”大,过渡过程平稳,因此,相角裕量越大,系统越稳定,足够大的相角裕度是保证系统鲁棒性的重要条件并使系统具有良好的暂态特性。为此,需引入反馈控制回路提高相角裕度,在下文进行讨论。
3 Buck电路控制回路信号模型建立
图3是Buck变换器S域反馈控制回路,其中的GP(s)为系统功率级传递函数,Kd(s)为模数转换器ADC的传递函数,Fm(s)为DPWM的传递函数,Gc(s)为在连续域中补偿器的传递函数,Gc(z)为离散后补偿器的传递函数。

图3 Buck变换器S域反馈控制回路Fig.3 The S phase feedback control circuit of Buck converter
3.1 ADC与DPWM对控制回路的影响
Kd代表模数转换器ADC的增益,如果模数转换器的位数已经确定,则此增益值也确定了。Fm代表数字脉宽调制器DPWM的增益,同理,如果数字脉宽调制器的位数确定了,则增益值Fm也确定了。其传输函数为

要达到精度10 mV,可算出ADC精度为
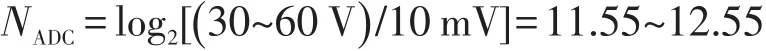
取NDPWM=13 bit,Ku=0.25,NADC=12 bit,设计的参考电压UADref=2.5,代入式(8)和式(9)得到:
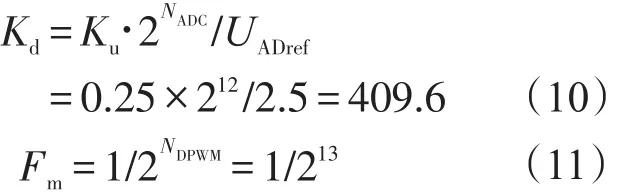
定义Gp(s)=KdFmGvd(s),将参数代入可得:

3.2 控制回路加入补偿器
可以通过Matlab中SISO(single input single output)设计工具来设计所需的补偿器。SISO Tool主要用于对单输入单输出控制系统补偿器的设计。SISO不仅可在时域和频域中设计补偿器,还可以直接看到其根轨迹、穿越频率和相角裕度等设计补偿器时的一些重要参数。在图形化界面上,通过鼠标移动或添加零极点等来调节补偿器的传输函数曲线,最终可以得到满意的补偿器。
利用SISO Tool求得补偿器的传递函数,计算过程中的操作界面以及计算结果如图4所示。
由图4可得补偿器的传递函数为
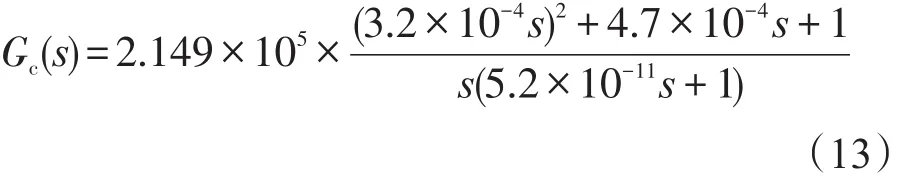
在系统中加入补偿器,通常是为了得到所希望形状的开环系统的频率特性。一般而言,在低频段增益充分大,以保证稳态误差要求;中频段对数幅频特性斜率一般为-20 dB/dec并占据足够宽的频带,以保证具有适当的相角裕量;高频段增益尽快衰减,以削弱噪声的影响。
通过使用Matlab/SISO得到系统补偿器的传输函数后,需要离散化模拟PID补偿器和补偿器的传递函数,根据离散化后两补偿器的传递函数进行对比以设定数字PID的各系数。
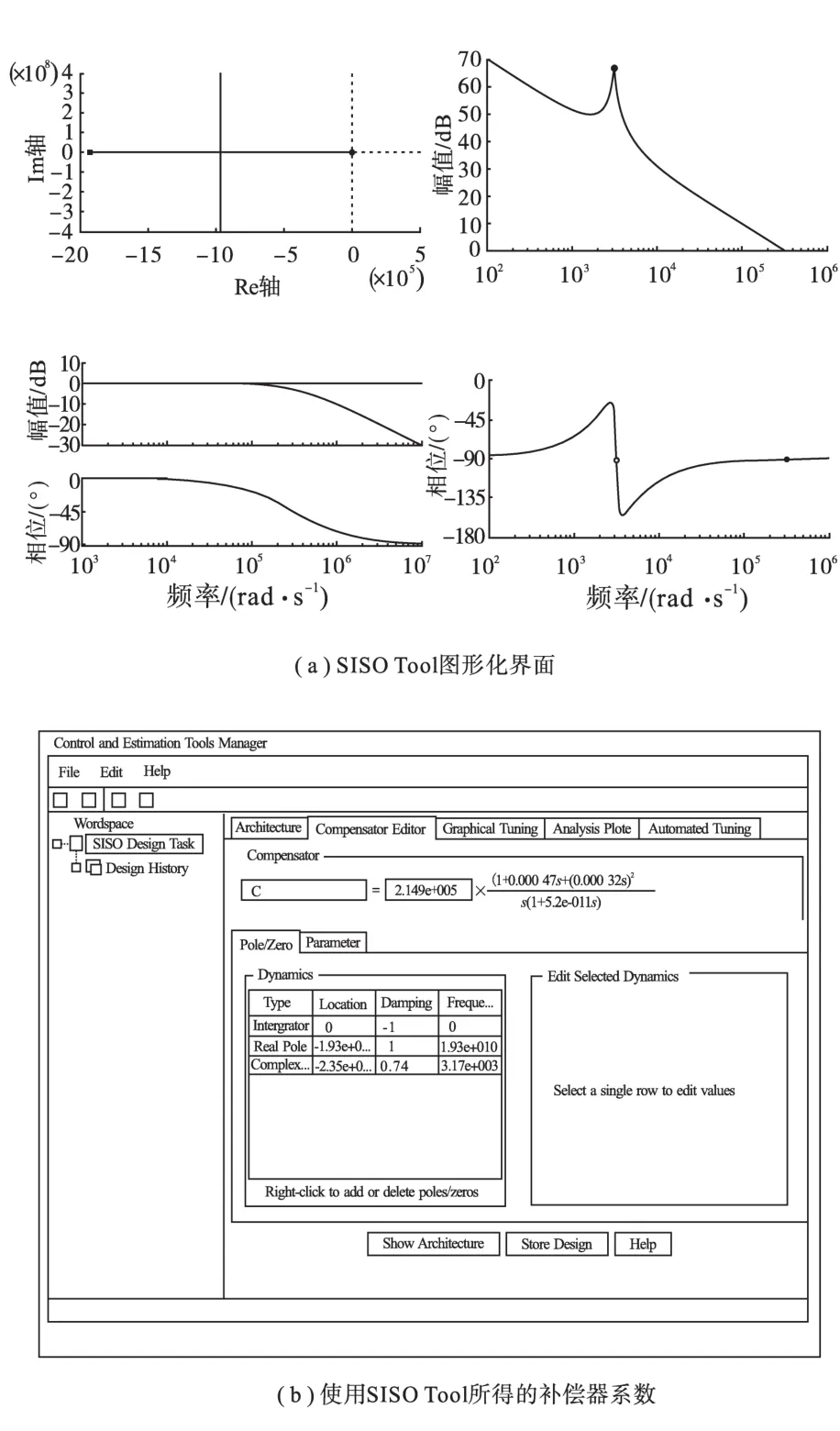
图4 SISO Tool使用界面Fig.4 SISO Tool platform interface
在数字电源中,通常PID控制器是作为补偿器使用的,其特性主要由积分项系数ki、比例项系数kp和微分项系数kd3个参数决定。比例项系数kp可使瞬态误差信号产生时控制器得以做出响应;微分项系数kd可以使系统阻尼效果得到提升;积分项系数ki可以对系统稳态误差进行消除。增加比例项系数kp可以减小调节的建立时间并减小系统的稳态误差来提高控制精度,但如果增加得过大,则会使系统产生不稳定,会发生振荡;过大的积分项系数ki增加建立时间,同时也会使系统不稳定;增加微分项系数kd可以提高建立时间,可以提高系统的动态响应能力,但如果使kd过大,会使调节作用过强,引起系统超调和振荡。
PID控制器的一般形式为
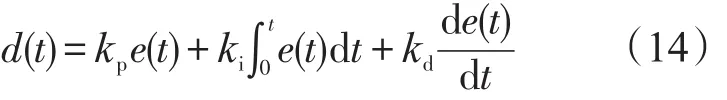
式中:d(t)为控制的输出;e(t)为输入的误差信号。
对应的传递函为
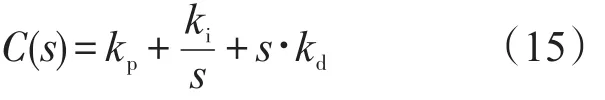
采用向后差分法来得到补偿器的离散形式:

对式(16)进行离散,可以获得差分方程为
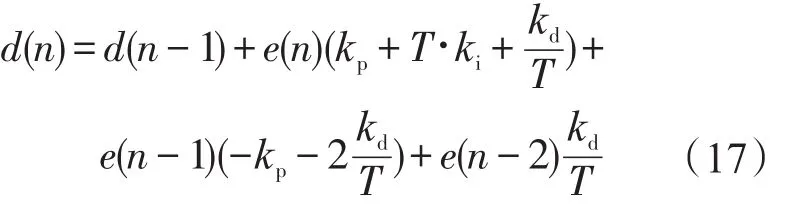
计算完成后的数字PID结构框图如图5所示。

图5 数字PID结构框图Fig.5 The structure block diagram of digital PID
将式(17)改写为

其中
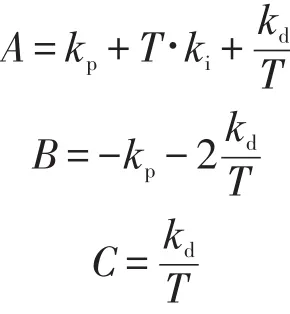
使用零极点匹配法对补偿器Gc(s)进行离散化。零极点匹配法即按规则将连续域中G(s)的零点和极点映射到离散域D(z)中。由于G(s)和D(z)具有相同的稳态直流增益,所以当G(s)稳定时,D(z)也一定稳定。在高频段,零极点匹配法可以得到比较好的效果。式(18)经过Matlab零极点匹配法变换后,得到补偿器的传递函数:

将式(19)分子分母同除以z-2,得:

将式(20)写成离散形式:

因此,可得PID各项系数:A=1 153,B=-2 200,C=1 051。
4 数控Buck变换器的仿真
利用Matlab/Simulink对所设计的Buck电路进行仿真,数控Buck电路如图6所示。
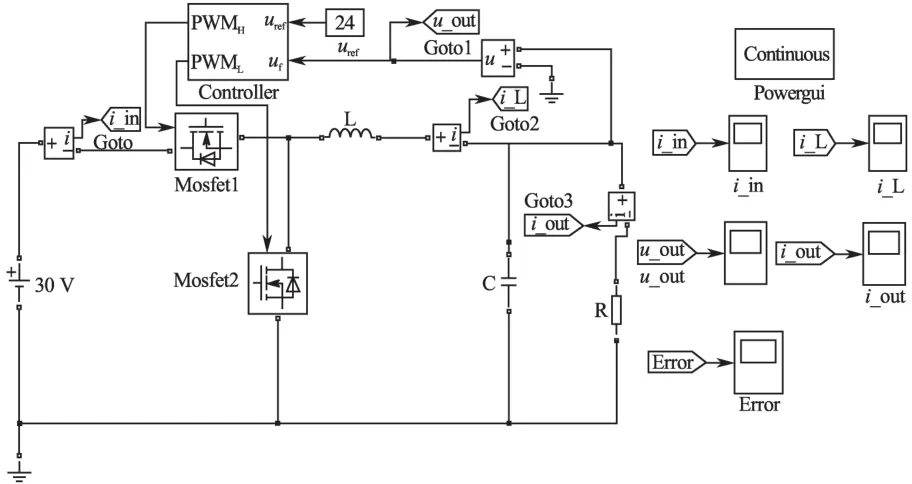
图6 数控Buck电路图Fig.6 The diagram of digital control Buck
图6 中,各个元件的参数分别为:L=0.5 mH,C=0.2 mF,R=24 Ω。本文所使用的是S域电压反馈控制对Buck电路进行控制,在控制回路中参考电压为24 V。通过对输出电压、输出电流、电感电流和回路误差来对Buck电路进行分析。
数控Buck电路回路中PWM部分如图7所示。
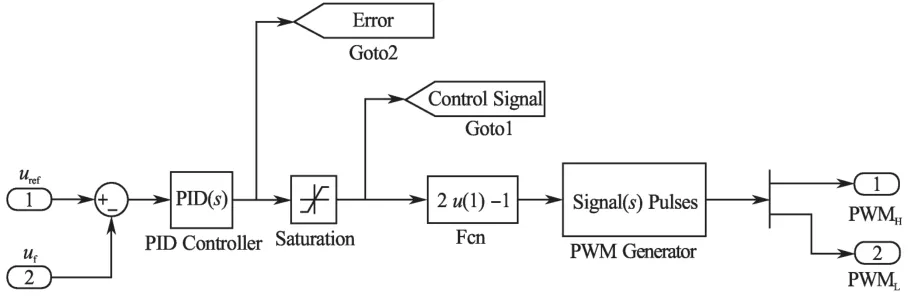
图7 数控Buck电路回路中PWM部分Fig.7 The PWM part of digital control Buck converter
图7 中,先将输出电压与参考电压信号相比较,再通过PID调节,给PWM发生器信号,并由PWM信号控制MOSFET的开通与关断。
电源变换电路的仿真结果如图8所示。

图8 输出电压Uo波形图Fig.8 The oscillation of output voltage Uo
从图8中可知,经过前期的震荡后,大概在0.025 s后输出电压趋于稳定,由此可知,所设计的Buck电路有很好的快速性。在系统稳定后输出电压稳定在24 V,其稳定性与准确性都比较满意。
图9为稳定后的电感电流iL的波形图。由图9可知,稳定后电感电流处于连续导电模式,电感电流的平均值在1A左右,可知系统基本满足要求。

图9 稳定后的电感电流iL的波形Fig.9 The stable oscillation of waveform inductance currentiL
图10为稳定后输出电流io的波形。

图10 稳定后输出电流io的波形Fig.10 The stable oscillation of output current iL
通过图10可知,在系统稳定后输出电流的纹波比较小,其平均值在1 A左右,满足最大输出电流的要求。
电路经过PID调节后的误差如图11所示。

图11 电路经过PID调节后的误差Fig.11 The relative error after PID adjustment
由图11可知,前期的误差值比较大,振荡也十分严重,但是经过0.025 s后,系统基本趋于稳定,且稳态误差基本保持为0,由此可知系统有很好的快速性、准确性和稳定性,系统总体满足要求。
5 结论
本文对数控Buck电路及其反馈控制回路进行原理阐述和理论分析,并在此基础上设计了输入直流电压30~60 V,输出直流电压24 V的DCDC电源变换器,最后通过软件仿真验证了所设计数控Buck电路的可行性。
研究结果表明,利用传统的数字控制Buck电路,采用状态空间平均法进行建模,并且引入S域电压反馈控制回路、添加PID补偿器,可实现稳定有效的DC-DC电源转换。本文提出的电源转换器,在0.025 s后便可达到稳定的直流低电压输出,具有良好的快速性;在系统稳定后输出电流的纹波比较小,输出电流的平均值在1 A左右,满足最大输出电流的要求;稳定后电感电流处于连续导电模式,其平均值在1 A左右,满足基本要求。
[1]张占松、蔡宣三.开关电源的原理与设计[M].北京:电子工业出版社,1998.
[2]吴爱国,李际涛.DC-DC变换器控制方法研究现状[J].电力电子技术,1999,33(2):75-78.
[3]严仰光.双向直流变换器[M].南京:江苏科学技术出版社,2004.
[4]Lee Tae-Won,Kim Sung-Ho,Yoon Yong-Ho,et al.A 3 kW Fuel Cell Generation System Using the Fuel Cell Simulator[J].Industrial Electronics,IEEE International Symposium,2004,3(2):833-837.
[5]Middlebrook R D.Null Double Injection and the Extra Element Theorem[J].IEEE Trans.Educ.,1989,32(3):167-180.
[6]Jang Y,Erickson R W.Physical Origins of Input Filter Oscillations in Current Programmed Converters[J].IEEE Trans.Power Electron.,1992,7(4):725-733.
[7]Verghese C G,Bruzos C A,Mahabir K N.Averaged and Sampled Data Models for PCM Controlled:A Re-examination[J].in Proc.IEEE Power Electron.Spec.Conf.,Rec.,1989,33(2):3-13.
[8]Ridley R B.A New Small-signal Model for Current-mode Control.Roswell[M].GA:Ridley Eng.,Inc.,1999.
[9]Middlebrook R D.Topics in Multiple-loop Regulations and Current Mode Programming[J].in Proc.IEEE Power Electron.Spec.Conf.,Rec.,1985,2(2):716-732.
[10]Middlebrook R D.Modeling a Current-programmed Buck Regulator[J].In Proc.IEEE Appl.Power Electron.Conf.,Rec.,1987,19(3):3-13.
[11]Bryant B,Kazimierczuk M K.Voltage-loop Power-stage Transfer Functions with MOSFET Delay for Boost PWM Converter Operating in CCM[J].IEEE Trans.Ind.Electron.,2007,54(1):347-353.
[12]Bryant B,Kazimierczuk M K.Voltage Loop of Boost PWM DC-DC Converters with Peak Current-mode Control[J].IEEE Trans.Circuits Syst.,2006,53(1):99-105.
Simulation Study on the DC-DC Power Source Converter Based on Digital Control Buck Circuit
KONG Weigong1,LI Lirong1,JIA Yaohua2
(1.Department of Electrical Engineering,Xingtai Polytechnic College,Xingtai 054035,Hebei,China;2.Hebei Daming County Power Supply Company,Handan 056900,Hebei,China)
The possibility of digital control application in middle and low power DC-DC conversions are more and more outstanding.Based on the digital control Buck circuit,a power source convert circuit of 30~60 V DC input to 24 V DC output was proposed.And the feasibility of the proposed Buck circuit was verified by the software simulation.During the design of the DC-DC power source convertor,the state space average method was used to establish the basic circuit model,and the S phase voltage feedback control circuit,as well as the PID compensator was applied to achieve the stable efficiency of DC-DC converting.The conclusions can provide certain references for the design and optimization of DC-DC converting circuit.
digital control Buck converter;status space average method(SSAM);digital PID compensator;DC-DC conversion
TM46
A
10.19457/j.1001-2095.20171007
河北省教育厅青年基金项目(2010283);河北省科技厅科技支撑项目(13211718)
孔维功(1979-),男,硕士,副教授,Email:kwgllrlw@163.com
2016-10-28
修改稿日期:2017-04-12

