永磁同步电机反步法与最大输出功率协调控制
王艳,于海生
(青岛大学自动化与电气工程学院,山东 青岛 266071)
永磁同步电机反步法与最大输出功率协调控制
王艳,于海生
(青岛大学自动化与电气工程学院,山东 青岛 266071)
针对单独使用一种方法难以实现对永磁同步电机速度伺服系统快速、高效的控制问题,设计了基于反步法和最大输出功率原理的端口受控哈密顿协调控制方案。利用反步法解决系统的快速响应问题,应用最大输出功率原理使电机输出最大功率,采用指数函数作为协调函数来实现协调控制策略,从而适应永磁同步电机的负载扰动。仿真实验表明,该永磁同步电机速度控制系统的协调控制方案有效地结合了反步法和最大输出功率原理的端口受控哈密顿协调控制的优点,使系统的动态性能和稳态性能优良,且能够在负载扰动时快速消除误差。
永磁同步电机;反步法;最大输出功率;端口受控哈密顿;协调控制
由于永磁同步电机(PMSM)具有能耗低、效率高和运行可靠性强等优点,使其在工业、农业、军事等自动化领域发挥了重要作用[1]。在对具有非线性的PMSM速度系统进行控制时,传统的矢量控制与直接转矩控制等对电机速度信号的处理过于简单,不能及时检测PMSM速度控制系统的瞬态变化并做出及时的响应[2]。模糊控制虽不需建立系统精确的数学模型,但因其控制精度不高,系统仍会存在一定的稳态误差,其稳定性问题还有待解决[3]。神经网络控制算法较复杂,给控制器的求取和实现增加了难度[4]。滑模控制实时性好,但却使系统存在抖振现象[5]。自适应控制响应迅速,但参数设置难度较大[6]。反馈线性化控制能够实现对电机的解耦控制,但在电机转速发生跳变时响应超调较大[7]。反步法控制是通过设计子系统的虚拟控制律来一步步反向推导到整个系统的控制,能保证系统的稳定性[8-9]。端口受控哈密顿(port-controlled Hamiltonian,PCH)控制设计较为简单,该方法也简化了系统的稳定性分析过程[10]。现有的永磁同步电机控制方法繁多,但可根据其控制目标分为2类:一类是将电机看作把输入信号变成输出信号的信号变换装置,控制目标是使系统能够快速跟踪给定信号;另一类是将电机看作把输入能量变成输出能量的能量变换装置,控制目标是优化控制整个系统的输入能量、输出能量和损耗能量,使系统的总损耗能量最小[11]。
本文选取隐极式永磁同步电机为研究对象,设计了反步法与最大输出功率协调控制的PMSM速度控制方案。反步法作为信号控制方法,提高系统的跟踪性能,使系统快速进入稳态;最大输出功率原理的PCH控制作为能量控制方法,保证系统输出最大功率,并优化系统稳态性能。为了减少复杂的自适应反推,设计负载观测器估计未知的负载转矩,使电机能够快速跟踪速度信号。针对电机的瞬态变化,设计了协调控制策略。协调控制策略调节两种方法的控制力度,使系统的瞬态变化得到快速的检测和响应。在系统的速度误差超过协调控制策略判断条件中的速度误差设定值时,重新投入动态性能良好的反步法控制,使系统尽快进入稳态运行后,最大输出功率原理的PCH控制起主要控制作用,使系统的稳态性在良好保持的同时能够输出最大功率。根据本文的设计思路,文献[5,8]等提出的两种方法共同控制的方案属于典型的信号控制,每种控制方法在各个时间段的作用力度是相同的,不能高效地利用每种控制方法的优点,而本文加入了能量方面的考虑,协调控制策略的设计使具有良好快速性的反步法控制在系统速度误差较大时起主要控制作用,稳定性良好的最大输出功率PCH控制则在稳态时起主要控制作用,当系统出现参数变化引起电机速度的大幅度改变时,便会投入信号控制使其迅速达到稳态,进入稳态后,能量控制方法起到主导控制作用。每种控制方法的优点都能在相应的时间点得到最高效的利用,具有较好的应用价值。
1 永磁同步电机数学模型
在d-q同步旋转坐标系下,PMSM的速度系统模型可表示为[12]
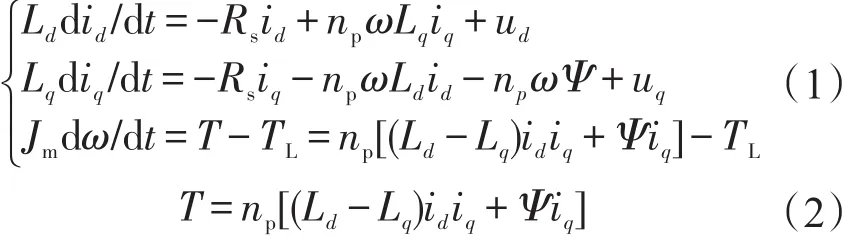
式中:ud,uq分别为 d,q轴定子电压;id,iq分别为d,q轴定子电流;Ld,Lq分别为d,q轴定子电感;Rs为定子电阻;Ψ为永磁体产生的磁链;Jm为转动惯量;np为极对数;ω为转子机械角速度;T为电磁转矩;TL为负载转矩。
2 永磁同步电机速度的协调控制原理
基于反步法与最大输出功率协调控制的永磁同步电机速度控制系统框图如图1所示,该系统采用基于=0的控制。
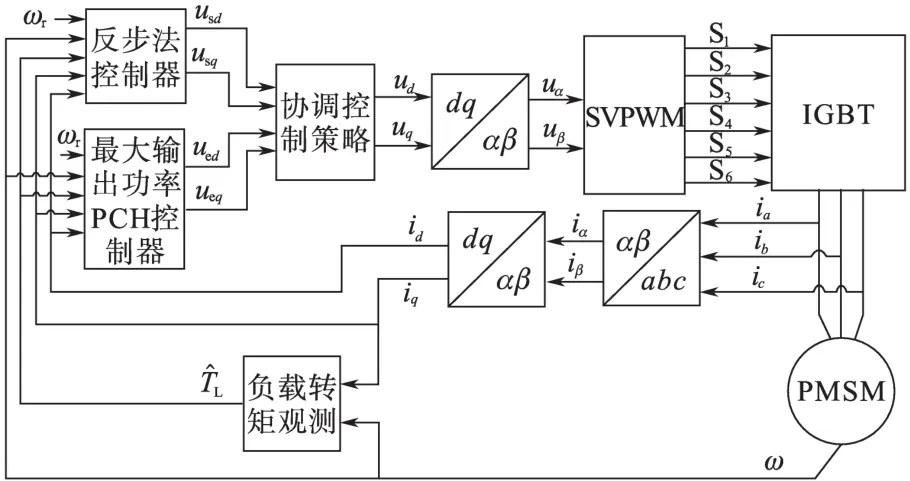
图1 基于反步法与最大输出功率协调控制的PMSM速度系统框图Fig.1 The block diagram of PMSM speed system based on backstepping and maximum output power coordination control
2.1 反步法控制器设计
反步法可以通过给分系统设计Lyapunov函数,逐步反向代入其中推导,直至找到系统的控制输入,而在反步法中引进的虚拟控制律,也由后面的分系统反向推导,使前面的子系统稳定,从而推导至整个系统稳定。
设该PMSM系统速度的给定值为ωr,速度跟踪误差为eω=ωr-ω,求其导数,联立式(2),得:



其中 k1>0
由于Ld=Lq=L,参考电流

把iqr代替iq带入式(3),可得:



其中 k2>0
把式(7)代入式(6),可得:



其中 k3>0
把式(10)代入(9),有


综上所述可知,系统的反步法控制器为
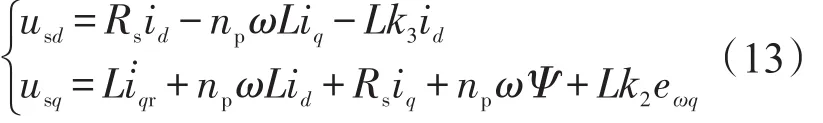
2.2 最大输出功率控制器设计
根据最大输出功率控制原理可知,输入功率随着定子电流的增大而增大,当其达到最大值时,相应的输出功率也处于最大值[13]。当PMSM运行于某特定转速ω时,如果满足

则系统的输入功率最大,P1为输入功率,当输入功率最大时,定子电流的变化率为零,系统进入稳态,电机交直轴电流变化率为零,由式(1)可得输入功率表达式为

由电压方程

可得:

式中:ulim为d-q坐标轴下PMSM最大基波相电压有效值。
将式(15)、式(16)代入式(14)并忽略定子电阻,可求得:

其中

式中:ρ为电机的凸极率,ρ=Lq/Ld。
当电机稳定运行时,若定子电流满足式(17)、式(18),那么此时PMSM的输入功率最大,对应的输出功率也最大。
定义该永磁同步电机速度控制系统的状态向量、输入向量分别为
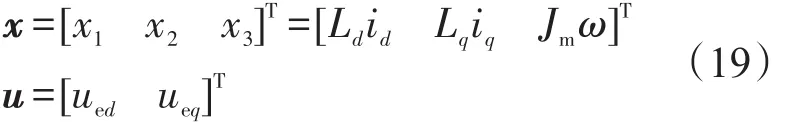
式中:ued,ueq为图1与式(1)中 ud,uq对应的PCH控制器的d,q轴定子电压。
取PMSM系统的Hamilton函数为

则式(1)系统的PCH模型为
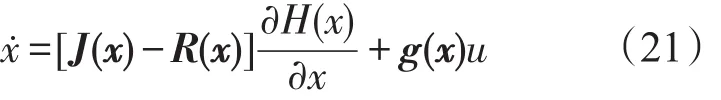
式中:R(x)为半正定对称矩阵,R(x)=RT(x)≥0;J(x)为反对称矩阵,J(x)=-JT(x)。
由式(1)可得PMSM的PCH模型为

对于给定的速度信号ωr,当负载转矩恒定已
知时,联立式(1)、式(17)可得系统的平衡点为[14]

选取

由式(20)~式(24)可得控制器为[15]

当负载转矩未知时,设计负载转矩观测器为

当负载已知时,有
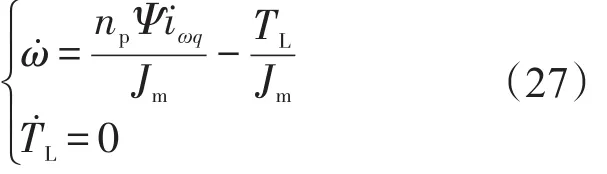

式(28)的特征方程为s2+c1s-c2/Jm=0。设系统式(27)的极点 sp(sp<0),则有在负载转矩未知时,用代替式(23)中的TL0,只有 iq0与 TL0有关,故用代替 iq0,则此时系统的反步法控制器与最大输出功率控制器分别为
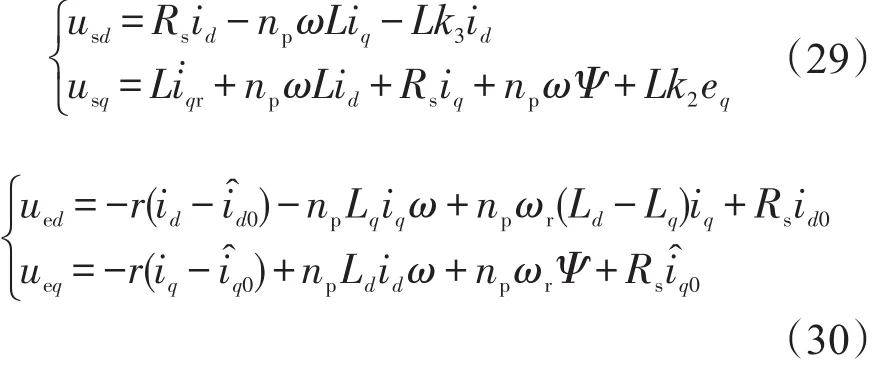
3 反步法与最大输出功率协调控制策略的设计
从信号与能量的角度看,反步法和最大输出功率控制具有互补性。本文设计的协调控制策略使系统在动态时以作为信号控制方法的反步法为主,稳态时以作为能量控制方法的最大输出功率控制为主,从而具有快速的动静态响应和最大的输出功率,达到期望的控制效果。
3.1 协调控制策略设计
定义csd,ced,csq,ceq分别是系统反步法控制器和最大输出功率的PCH控制器d,q轴的协调函数,设|ω-ωr|>β(β 为常数,且 β>0,rad/s)的开始时刻为t1。因此协调函数可设计为

式中:Tc为协调时间常数。
很显然
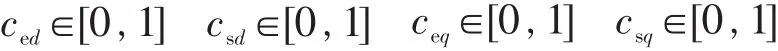
从而协调控制策略为
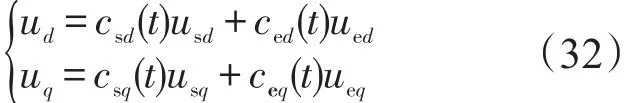
3.2 基于反步法与最大输出功率协调控制的PMSM速度系统的稳定性分析
3.2.1 反步法控制子系统稳定性分析
对于利用反步法设计的误差变量 eω,eωq,eωd作为状态变量所组成的系统,定义Lyapunov函数:

对Vs求导,由式(9)、式(13)、式(16)可知:

3.2.2 PCH控制子系统稳定性分析
对于PCH子系统,定义Lyapunov函数:

很明显,Ve>0。由于Jd(x)为反对称矩阵,有

很显然,Vs正定,V̇s负半定。由Lyapunov稳定性理论可知,反步法控制子系统是渐近稳定的。
由于 Rd是正半定的,根据拉萨尔不变集定理有,如果该闭环系统包括在集合{x∈ Rn|[∂Hd(x)/∂x]TRd(x)[∂Hd(x)/∂x]=0}内的最大不变集为{x0},则哈密顿子系统在平衡点x0处是渐近稳定的。
3.2.3 整个系统稳定性分析
当时间t=0时,协调函数 csd(t)=csq(t)=1,ced(t)=ceq(t)=0,相当于只有反步法控制器作用于整个系统,整个系统稳定。
当时间t→∞时,协调函数csd(t)=csq(t)=0,ced(t)=ceq(t)=1,相当于只有最大输出功率的PCH控制器作用于整个系统 V=Ve>0 ,V̇=V̇e<0 ,整个系统稳定。
由以上分析可知,整个系统是渐近稳定的。
4 仿真实验及分析
针对反步法与最大输出功率协调控制的PMSM速度控制系统,采用Matlab/Simulink对反步法与最大输出功率协调控制的PMSM速度控制系统进行仿真,以验证该方法对PMSM速度系统的控制性能。仿真所用电机参数如下:Rs=2.875 Ω,Ld=Lq=8.5 mH, Ψ=0.175 Wb,Jm=0.02 kg∙m2,np=4,k0=1,r=10,Tc=0.1 s,sp=-500,k1=5 000,k2=k3=10 000,β=2。
基于dSPACE系统,搭建PMSM速度控制平台,直接采用Matlab/Simulink环境的控制器及模型进行实验,并对PMSM的速度特性进行实时监控。实验分别针对协调控制策略的可行性(见图2)、反步法单独控制(见图3)、最大输出功率的PCH单独控制(见图4)、两种方法协调控制(见图5)的情况进行验证,并对协调控制的跟踪特性(见图6)进行实验验证。链接平台设备,通过ControlDesk实时观测转子转速变化(见图7)。
对于图2~图5,在0~0.3s时,给定的速度信号ωr=100 rad/s;在0.3~1 s时,ωr=150rad/s。在0~0.6s时,给定负载转矩 TL=2 N∙m ;在0.6~1 s时,为5 N∙m。图2为协调时间常数不同时系统的速度响应曲线。图2中,由图中曲线可知,当Tc1
=0.2时,控制效果比较理想。由图3可以看出,反步法控制的响应速度快,但其稳态性能较差。图4中,与反步法控制相比较,最大输出功率控制的响应速度有待提高,尤其在0.6 s由于负载变化使速度产生较大误差时,响应速度要比反步法慢很多,跟踪性能较差。图5为Tc1=0.2时的协调控制曲线,在0.3 s和0.6 s时,系统转速和负载转矩突变,使得β=2,与图3~图4对比可知,该协调控制系统的响应速度与反步法基本一致,比最大输出功率原理单独作用时的响应速度有明显的提升,故协调控制策略在符合判断条件时能及时地投入反步法控制,保证系统动态性能和稳态性能。图6为协调控制系统的跟踪速度曲线,给定速度信号为正弦曲线,其幅值为150 rad/s,在0.6 s时,负载转矩TL由2 N∙m跳变为5 N∙m,从图中曲线中可以看出系统跟踪性能良好。图7为实验所测转子速度波形,在12 s时,TL为由2 N∙m变为5 N∙m,16 s时,负载恢复2 N∙m。经比较,协调控制方法有效地结合了反步法与最大输出功率PCH控制的优点,系统既能快速跟踪信号,又有很好的稳态性能和比较强的稳定性,同时能很好地适应负载变化。

图2 协调时间常数不同时的速度曲线Fig.2 The speed curves of different coordinate time constant

图3 反步法单独作用时的速度曲线Fig.3 The speed curve of backstepping control alone

图4 最大输出功率控制单独作用时的速度曲线Fig.4 The speed curve of maxmum output power control alone

图5 协调控制的速度曲线Fig.5 The speed curve of coordination control

图6 协调控制的转速跟踪曲线Fig.6 The speed tracking curve of coordination control

图7 协调控制系统速度实验波形Fig.7 The speed waveform of coordination control
5 结论
[1]柏建勇,滕青芳,杜永栋,等.永磁同步电机控制策略比较研究[J].控制工程,2015,22(3):490-494.
[2]向国菲,佃松宜,蒲明.基于EKF永磁同步电机无传感直接转矩控制研究[J].控制工程,2015,22(3):369-374.
[3]Ouledali O,Meroufel A,Wira P,et al.Direct Torque Fuzzy Control of PMSM Based on SVM[J].Energy Procedia,2015,74:1314-1322.
[4]Essalmi A,Mahmoudi H,Abbou A,et al.DTC of PMSM Based on Artificial Neural Networks with Regulation Speed Using the Fuzzy Logic Controller[C]//International Renewable and Sustainable Energy Conference(IRSEC),2015.
[5]卢涛,于海生,山炳强,等.永磁同步电机伺服系统的自适应滑模最大转矩/电流控制[J].控制理论与应用,2015,32(2):251-255.
[6]Kojabadi H M,Ghribi M.MRAS-based Adaptive Speed Estimator in PMSM Drives[C]//IEEE International Workshop on Advanced Motion Control,2006:569-572.
[7]Wu Zhengcheng.Feedback Linearization Control of PMSM Based on Differential Geometry Theory[C]//5th IEEE International Conference on Industrial Electronics and Applications,2010:2047-2051.
[8]纪志成,李三东,沈艳霞.自适应积分反步法永磁同步电机伺服控制器的设计[J].控制与决策,2005,20(3):329-336.
[9]Shan Bingqiang,Yu Haisheng,Yu Jinpeng.Position Control of the Permanent Magnet Synchronous Motor Based on Back-Stepping Method and Load Torque Observer[J].ICIC Express Letters,2013,7(3):735-740.
[10]Ortega R,van der Schaft A,Maschke B,et al.Interconnection and Damping Assignment Passivity-based Control of Port-controlled Hamiltonian Systems[J].Automatica,2002,38(4):585-596.
[11]Yu Haisheng,Yu Jinpeng,Liu Jin,et al.Nonlinear Control of Induction Motors Based on State Error PCH and Energy-shaping Principle[J].Nonlinear Dyn,2013,72(2):49-59.
[12]于海生,赵克友,郭雷,等.基于端口受控哈密顿方法的PMSM最大转矩/电流控制[J].中国电机工程学报,2006,26(8):82-87.
[13]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,1997.
[14]Yu Haisheng,Yu Jinpeng,Liu Xudong,et al.Port-Hamiltonian System Modeling and Position Tracking Control of PMSM Based on Maximum Output Power Principle[J].ICIC Express Letters,2012,6(2):437-442.
[15]Yu Haisheng,Yu Jinpeng,Wang Yong.Maximum Output Power Control of Permanent Magnet Synchronous Motor Based on Energy-shaping Principle[C]//Automation and Logistics,2007 IEEE International Conference on.IEEE,2007:2008-2012.
Permanent Magnet Synchronous Motor Control System Based on Backstepping and the Maximum Output Power Coordination Control
WANG Yan,YU Haisheng
(College of Automation and Electrical Engineering,Qingdao University,Qingdao 266071,Shandong,China)
In view of the problem that the fast and high-efficiency control of permanent magnet synchronous motor(PMSM)speed servo system with one control method is difficult to realize,a hybrid coordination control scheme based on backstepping and the port-controlled Hamiltonian(PCH)control on maximum output power principle was designed.The backstepping technique was used to optimize the dynamic response of the system,and the PCH control method was applied to ensure that the system reached its maximum output power.Furthermore,exponential function was utilized as the coordination function to fulfill the coordination control strategy.The coordination control system was well adapted to the load disturbance of PMSM.The simulation results show that the coordination control scheme which is applied to PMSM speed servo system combines the advantages of backstepping control and PCH control.The system has good dynamic and steady-state performance,and it can eliminate the error quickly under the external disturbances.
permanent magnet synchronous motor(PMSM);backstepping;the maximum output power;portcontrolled Hamiltonian;coordination control
TP273
A
10.19457/j.1001-2095.20171003
国家自然科学基金项目,永磁同步电动机驱动系统的信号与能量协调控制(61573203)
王艳(1990-),女,硕士研究生,Email:569317915@qq.com
2016-11-17
修改稿日期:2017-03-07

