基于Laplace变换的RLC电路特性研究与仿真

刘德全， 周国清

(1. 天津大学 微电子学院， 天津 300072； 2.宁夏师范学院 物理与电子信息工程学院， 宁夏 固原 756000；3. 天津大学 遥感中心，天津 300072)

基于Laplace变换的RLC电路特性研究与仿真

刘德全1,2,3， 周国清1，3

(1. 天津大学 微电子学院， 天津 300072； 2.宁夏师范学院 物理与电子信息工程学院， 宁夏 固原 756000；3. 天津大学 遥感中心，天津 300072)

为了提高对电路中电阻、电感、电容的理解，对RLC串联二阶电路采用Laplace模型建立了传递函数，通过传递函数对电路的欠阻尼、临界阻尼和过阻尼的工作状态进行分析，对其状态轨迹、频率特性等进行了研究。在EDA软件平台中设计了RLC串联电路，对3种工作状态、状态轨迹以及频率特性曲线进行了仿真，得到了清晰的图形。

拉普拉斯变换； RLC电路； 传递函数； 动态特性

RLC二阶电路是最基本的电路之一，在RLC二阶电路分析和建模仿真、RLC串联谐振电路中的电感频率特性、二阶电路的衰减常数的估计、电路状态轨迹、方波激励下的二阶电路的响应、RC滤波器优化等方面受到重视并进行了很多研究[1-11]。但是，相关研究多为时域分析，而在s域中分析得较少。本文通过Laplace变换将时域分析转换为s域分析，方法简单易懂，很容易得到电路的3种工作状态、状态轨迹图和相关频率特性曲线。

1 s域电路分析

1.1 s域电路建模

RLC串联电路s域电路如图1所示[12-19]。

图1 RLC串联电路的s域电路图

设电感、电压的初始值为0，以电容电压Uc为输出变量，则电压传递函数的Laplace变换方程为

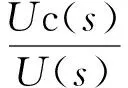
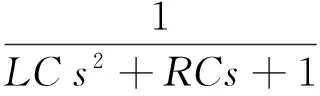
(1)

其中：

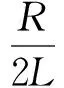
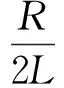
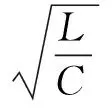
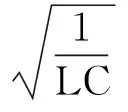
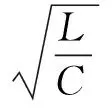
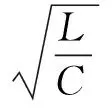
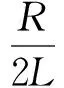
此时极点位于负实轴上，H(s)分母有(s-p1)和(s-p2)因子，它的自由响应函数包含2个不同的A1ep1tε(t)， (p1<0)和A2ep2tε(t)， (p2<0)的衰减指数函数，且极点离原点越远，衰减得越快。自由响应与极点关系图如图2(c)所示。

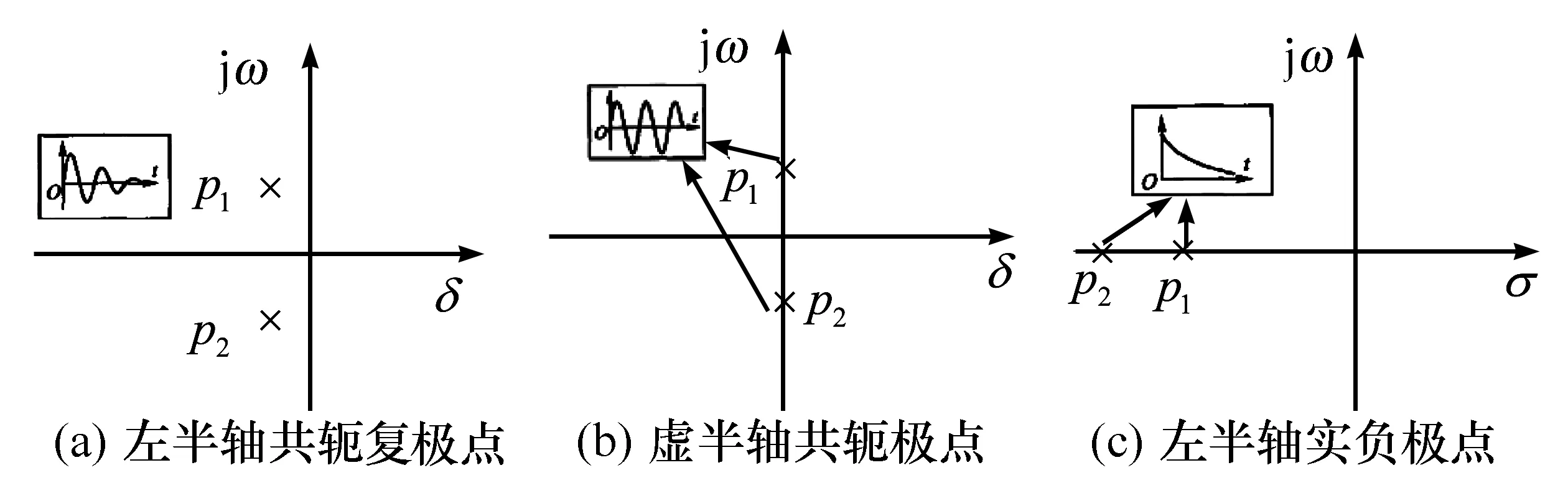
图2 极点与自由响应关系图

1.2 状态轨迹

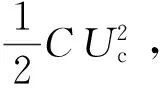
1.3 频率特性曲线

将s=jω代入(1)式，得到系统的频率响应传递函数为

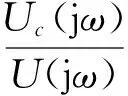
(2)

式中，|H(jω)|称为幅频响应，φ(ω)称为相频响应。当ω从0(或-∞)变动时，|H(jω)|和φ(ω)也随之变换，绘制出其随ω变化的曲线，就得到了幅频特性曲线和相频特性曲线。幅频特性曲线和相频特性曲线合称为频率特性曲线。如果在绘制曲线时，频率以对数尺度表示，则得到的图形分别称为幅频波特图和相频波特图，总称为波特图。

2 电路特性参数仿真

2.1 动态电路的暂态和状态轨迹

在EDA仿真软件[22]中绘制如图3所示电路。在图中，Oscilloscope为四通道示波器，其中A通道为Uc信号，B通道为IL信号，C通道为CLOCK信号(1 Hz、1 V的方波电压信号)。在进行状态轨迹仿真时，x轴为Uc信号，y轴为IL信号，H1为电流控制的电压源。由于该示波器只能采集电压信号，因此，需将电感的电流信号转换为电压信号(线性转换)。在该电路中，电流信号比较小，为了得到清晰的波形，其跨阻值设置较大，这里设置为500，即转换关系为

U=500IL

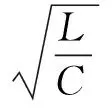
(1) 当开关处于“1”位置时，即R=500 Ω，电路处于过阻尼状态(仿真波形如图4所示)，在所有的CLOCK、Uc和IL波形图中，CLOCK信号为红色，Uc信号为绿色，IL信号为蓝色；

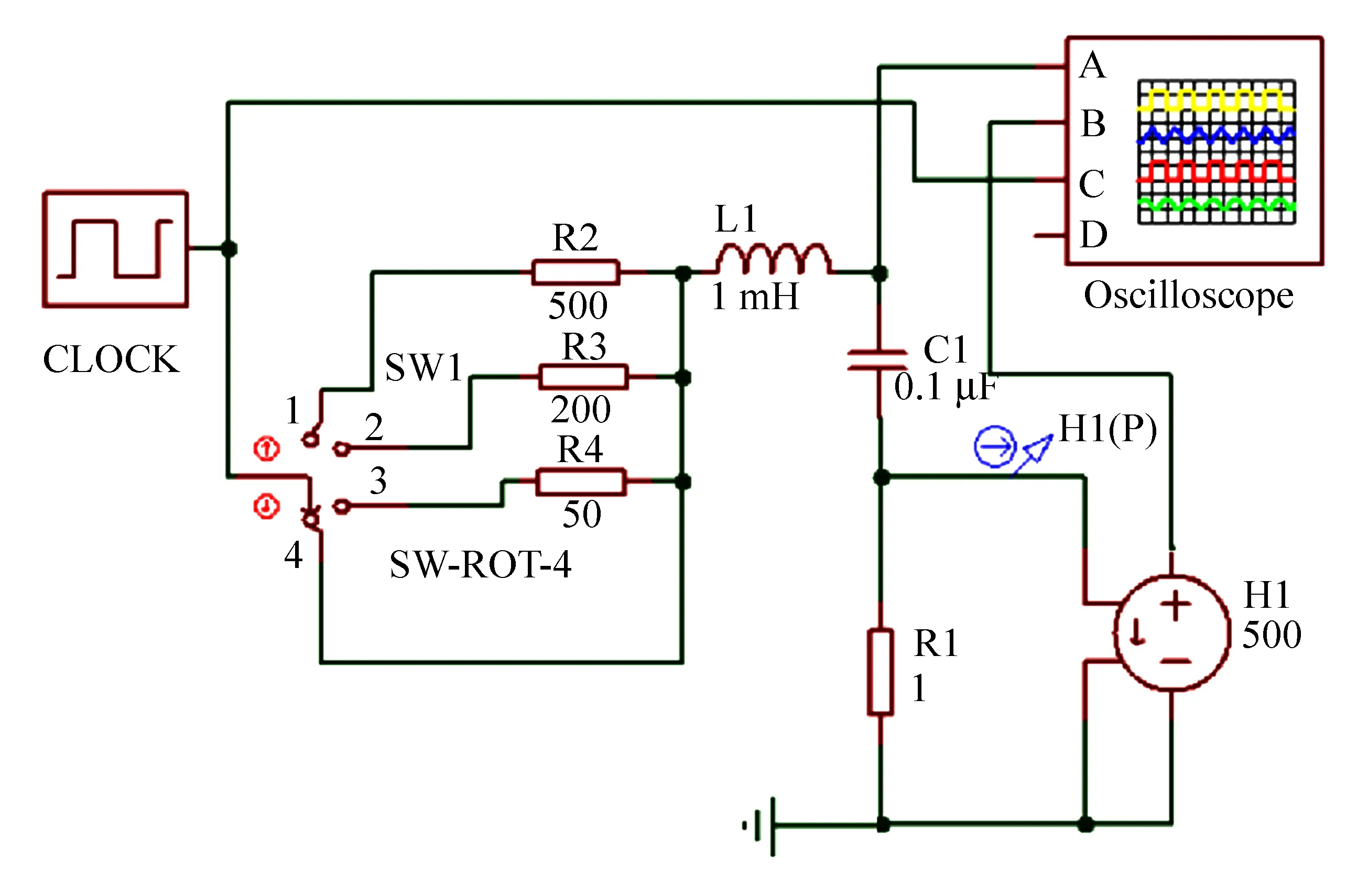
图3 仿真测试电路

(2) 当开关处于“2”位置时，即R=200 Ω，电路处于临界阻尼状态，仿真波形如图5所示；

(3) 当开关处于“3”位置时，即R=50 Ω，电路处于欠阻尼状态，仿真波形如图6所示；

(4) 当开关处于“4”位置时，即R=0 Ω，在理想电路时是等幅振荡，要得到等幅振荡波形，需要添加负阻抗元器件，在图3中没有负阻抗元器件，因此仿真波形应该是衰减的正弦波形，如图7所示。

2.2 电路频率特性曲线

按照图8(a)所示电路设计仿真电路，采用频率特性曲线图表进行仿真，仿真结果如图8(b)所示。其中，正弦波信号的频率为100 Hz，幅度为1 V；黑色的波形线为幅频特性曲线，红色的波形为相频特性曲线。很显然，该电路具有低通滤波器的特征。

图4 过阻尼状态波形

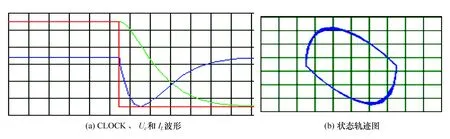
图5 临界阻尼状态波形

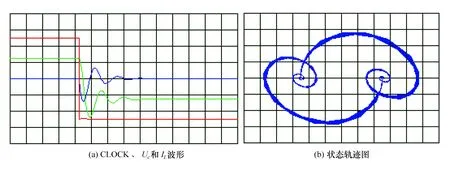
图6 欠阻尼状态波形

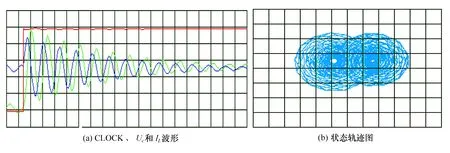
图7 R=0时的波形

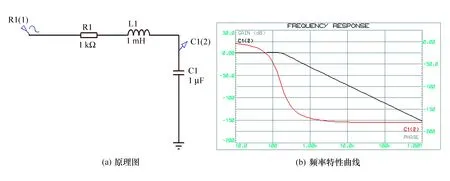
图8 频率特性曲线仿真

3 结语

在RLC二阶串联实验电路中，用Laplace变换对RLC电路的暂态过程、状态轨迹图和频率特性曲线进行分析，利用Proteus EDA软件对电路的特性进行仿真，参数修改非常方便，并且降低了实验成本、拓宽了实验教学空间，有助于学生加深对基本元器件特性的理解，激发学习的积极性。

References)

[1] 孙文杰.Matlab电路仿真实验常用建模方法[J].实验室研究与探索,2016,35(7):80-84.

[2] 郝小江.RLC串联电路暂态过程综合实验设计[J].实验科学与技术,2016,14(1):39-41,94.

[3] 任兆香,顾海清,张倩，等.PSPICE仿真分析与二阶动态电路教学法研究[J].实验技术与管理，2016,33(6):117-125.

[4] 陈国杰,陈奎,周有平，等.电感频率特性及在RLC串联谐振电路中的应用[J].大学物理,2016,35(6):29-32.

[5] 刘松龄,熊新兵,陈首部，等.二阶电路衰减常数的估计及误差分析[J].中南民族大学学报(自然科学版),2015,34(2):100-103.

[6] 李瑞金.二阶电路衰减系数的误差分析[J].实验科学与技术,2015,13(5):32-34.

[7] 李姿,李曼，王津.二阶电路暂稳态过程与状态轨迹的实验研究[J].科技论坛，2013(8)：37-38.

[8] 陈杰,贺泽东,南楠.方波电动势激励下的RLC串联电路共振特性研究[J].大学物理,2016,35(1):28-30.

[9] 刘晓文,薛雪,乔欣，等.方波激励下的RLC串联电路暂态响应仿真研究[J].实验技术与管理,2015,32(1):112-115.

[10] 刘洪臣,陈东,刘雷.方波输入下LC电路暂态过程实验研究[J].实验技术与管理,2014,31(2):23-25.

[11] 田聪.RC有源滤波器的优化设计[D].金华:浙江师范大学,2016.

[12] Hambley A R.电工学原理与应用[M].熊兰,彭光金,孙韬，等译.北京：电子工业出版社,2014.

[13] 吴大正.信号与线性系统分析[M].北京:高等教育出版社,2005.

[14] 邱关源,罗先觉.电路[M].北京:高等教育出版社,2008.

[15] Alexander C K, Sadiku M N O.电路基础[M].段哲民,周巍,李宏，等译.北京:机械工业出版社，2014.

[16] 秦曾煌.电工学[M].北京:高等教育出版社,2009.

[17] Nilsson J W, Riedel S A.电路[M].周玉坤,冼立勤，译.北京:电子工业出版社,2015.

[18] 郑君里,应启珩,杨为理.信号与系统[M].北京:高等教育出版社,2011.

[19] 胡寿松.自动控制原理[M].北京:科学出版社，2013.

[20] 天煌科技实业有限公司.THKKL-2型控制理论实验箱实验指导书[EB/OL].(2010-12-03)[2017-04-10].https://wenku.baidu.com/view/14497b0bbb68a98271fefab3.html.

[21] 南京恒缔科技有限公司.HD8662信号与系统实验讲义正文[EB/OL].[2017-04-10].http://www.docin.com/p-218347090.html.

[22] 刘德全.Proteus 8：电子线路设计与仿真[M].北京:清华大学出版社,2017.

Research and simulation of RLC circuit characteristics based on Laplace transform

Liu Dequan1,2,3， Zhou Guoqing1,3

(1. School of Microelectronics, Tianjin University, Tianjin 300072, China; 2. School of Physics and Electronic Information Engineering, Ningxia Normal College, Guyuan 756000, China；3. Remote Sensing Center, Tianjin University, Tianjin 300072, China)

In order to improve the understanding of RLC (resistance, inductance and capacitance) in the circuit, the transfer function is established by using the Laplace model for the RLC series two-order circuit. Through the transfer function, the working states of the underdamping, the critical damping and the overdamping of the circuit are analyzed, and their state trajectories and frequency characteristics, etc., are studied. The RLC series circuit is designed at the EDA software platform. The three working states, the state trajectories and the frequency characteristic curves are simulated, and the clear graphs are obtained.

Laplace transform; RLC circuit; transfer function; dynamic characteristics

TM133；TP391

A

1002-4956(2017)10-0108-04

10.16791/j.cnki.sjg.2017.10.027

2017-04-20修改日期2017-06-05

宁夏教育厅高等学校科学研究项目(NGY2016200)；宁夏高等学校本科教学质量与教学改革项目(2017(68));国家海洋局区域经济创新示范项目(cxsf-039)

刘德全(1977—)，男，甘肃白银，硕士，副教授，主要研究方向为电路仿真设计及信号处理.

E-mail：ldqzhh@163.com