小角度Rutherford散射模拟与研究
周 伟, 李 聪, 李佳惠
(中国石油大学(华东) 理学院, 山东 青岛 266580)
小角度Rutherford散射模拟与研究
周 伟, 李 聪, 李佳惠
(中国石油大学(华东) 理学院, 山东 青岛 266580)
以单靶核Rutherford散射的计算机模拟程序为基础,编写了多靶核Rutherford散射的模拟程序。应用多靶核模拟程序直观地研究了多次散射、靶核遮掩、电子屏蔽等影响Rutherford散射公式适用性的因素,更好地理解和分析了小角度Rutherford散射的物理图像,并通过对不同因素的对比分析,找出了影响小角度Rutherford散射的主要因素。
Rutherford散射; 计算机模拟; 多次散射; 靶核遮掩; 电子屏蔽
1 Rutherford散射实验
Rutherford散射实验也被称为α粒子散射实验,是近代物理科学发展中最具影响力的重要实验之一。该实验不但证明了核式模型的正确性,而且为人们提供了一种研究物质结构的方法。Rutherford背散射成为一种分析材料的重要技术手段,广泛应用于固体物理、表面物理、材料物理以及微电子物理学等方面,并以此为基础发展了很多新的技术,如表面组分含量分析、薄膜厚度测量、杂质分析等,这些技术被广泛地应用在科学研究和工程建设中[1-2]。
在Rutherford散射实验中,散射截面可以由Rutherford公式计算,但当散射角小于45°或散射角接近于180°时,Rutherford公式给出的结果与实验结果有较大的差异[3]。吴去非近似地确定了在小角度内保证Rutherford公式有效性的极限角度[4];马晓栋等研究了α粒子束的展宽对Rutherford散射的影响[5];任玉安讨论了影响Rutherford散射的因素是一次散射假定的有效性[6]。
本文利用计算机模拟找出Rutherford公式在小角度范围内不适用的原因。文献[7]基于蒙特卡罗方法和单次散射轨迹模拟,建立了一套能有效地模拟在单靶核作用下α粒子散射的计算机模拟程序并对其进行了优化。本文以该方法为基础,编写了多靶核Rutherford散射的模拟程序[7-8],并且应用多靶核模拟程序更加直观、有效地研究了多次散射、靶核遮掩、电子屏蔽等多种因素对Rutherford散射的影响,更好地理解了小角度的Rutherford散射及其相关理论。
2 程序设计
与单靶核Rutherford散射过程的模拟[7]相同,多靶核模拟过程也分成初始化、单次散射轨迹的模拟、蒙特卡洛模拟及散射概率统计4部分。但与单靶核模拟过程有两点不同之处:一是在初始化中,需要将单个靶核扩展到多个靶核,这里的关键是给定靶核的排布;二是在单次散射轨迹的模拟中,需要考虑多个靶核对入射粒子的共同作用。
在Rutherford散射公式的推导过程中[9-11],一般认为当金箔比较薄时,原子核具体在金箔的哪一层对散射过程的影响不大。我们在最初的研究中,假定金箔内的原子核可以压缩到一层上,在该层上原子核的分布是均匀的,并且以方格形状排列。
在计算机模拟中,靶核个数越多,模拟结果越准确,越能够消除因靶核个数少而带来的边界效应。但靶核数目越多、计算入射粒子受到的力时需要的计算资源就越多,计算时间就越长。研究后发现,当靶核个数为25时,既可以有效地消除边界效应的影响,又可以将模拟时间控制在合理的范围之内。
另外,本文还研究了靶核间距对模拟结果的影响,将靶核间距分别取为金原子直径的1/50、1/100、1/200和1/300,分别模拟将50、100、200和300层金原子压缩到一层上的情况。最终发现,将靶核间距确定为1 350 fm(金原子直径的1/200)是比较合适的选择。
图1为不同模拟条件下的散射概率曲线,图中的点划线给出了在上述单层多靶核条件下模拟得到的散射概率,点线给出了单靶核条件下的散射概率。结果发现,在散射角90°附近单层多靶核条件下的概率明显出现一个下陷。分析原因:在单层多靶核散射中,当入射粒子被任意靶核散射约为90°时,其运行轨迹必然会离另外的靶核非常近,这种情况下入射粒子会被二次散射,并改变散射角,使得散射角为90°的概率被压低。这个压低是将原子核近似看成处在同一层所带来的必然结果。为了消除这种效应,将一层靶拆分成均匀分布的两层,每层的靶核个数仍为25个,每个层上靶核间距扩大为2 700 fm,两层上的靶核交错分布,如图2所示。经过对不同层间距下散射概率的对比分析发现,2个靶层之间的间距为900 fm时,模拟得出的散射概率在有效散射角范围内更接近单靶核条件下的散射概率。因此,将金箔简化为方格排布的2层靶,每层的靶核个数为25个,靶核间距为2700 fm,层间距取900 fm。
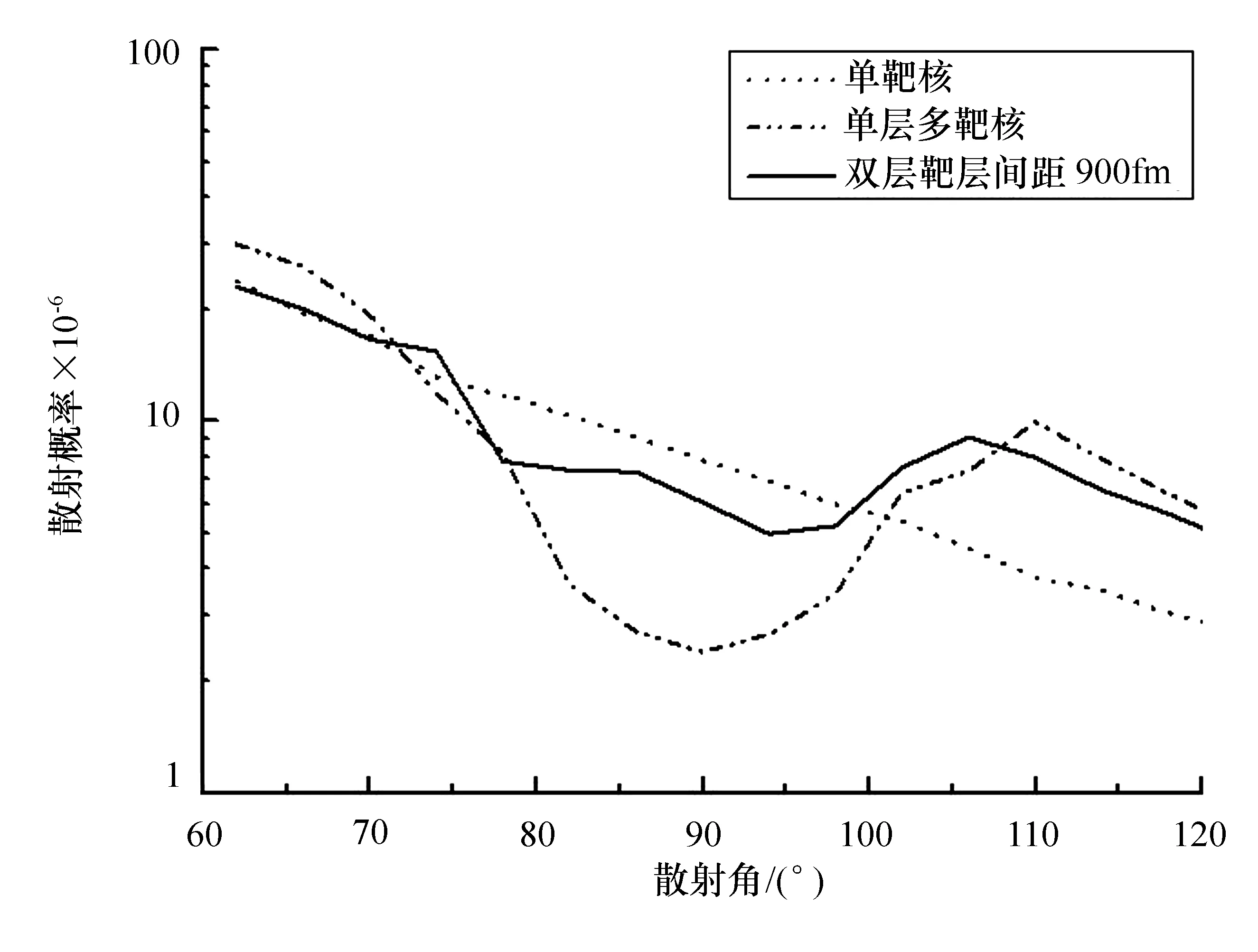
图1 不同模拟条件下的散射概率曲线
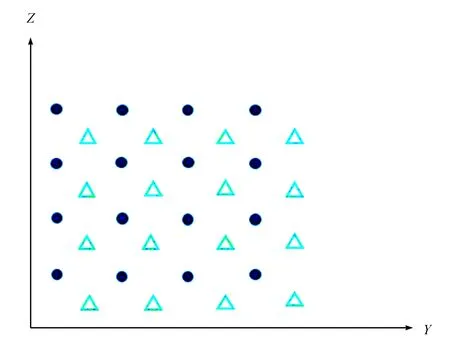
图2 双层靶核排布示意图
3 结果与分析
Rutherford散射公式推导中有4个假设:入射过程中靶核不动,金属箔中原子核前后不互相遮掩,通过金属箔的α粒子只经过一次散射,入射粒子不受核外电子影响[7,12]。这些假设在一定条件下是成立的,是Rutherford公式推导的前提。但对于小角度Rutherford散射,被散射的α粒子的碰撞参数较大,上述假设中有一些就不成立了,这也是Rutherford散射公式不能描述小角度Rutherford散射概率的原因。一般认为,影响Rutherford 散射公式适用性的因素可总结为靶核遮掩、多次散射和电子屏蔽。靶核遮掩是指2个或2个以上原子核对入射粒子的作用范围出现交叠,使入射粒子先后受到2个以上原子核的作用,即原子核之间不相互独立;而多次散射指的是入射粒子在散射过程中先后受到多个原子核作用。两者之间虽说法不同,但本质上都是入射粒子受到多个原子核作用。我们认为这是同种效应,在下面的分析中以多次散射统称。因此,判断影响小角度Rutherford散射的主要因素为多次散射和电子屏蔽。
3.1 多次散射
在多靶核Rutherford散射中,靶核层数越多,多次散射发生的概率越大。在之前的模拟中,我们给出了2层靶核的Rutherford散射概率。在此基础上,构建完全对称的三层靶,每层靶核的排布方式保持不变。图3给出了单靶核、双层多靶核和3层多靶核3种情况下Rutherford散射概率,可以看出随着靶核层数的增多,发生多次散射的概率增大,小角度范围内的散射概率有明显增大。对比单靶核Rutherford散射概率,双层靶核的散射概率有所增大,但增大的程度很小;而3层靶核的Rutherford散射概率在小角度范围内则明显增大。在0°~45°的小角度范围内,3层靶核的Rutherford散射概率先变大后变小,但整体上要显著地大于单靶核散射概率。
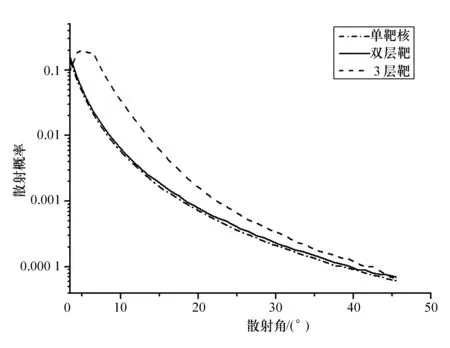
图3 不同层数下的散射概率曲线
3.2 电子屏蔽
电子屏蔽效应是指对于入射粒子来说,由于核外电子带负电而抵消了一部分核电荷,从而引起有效核电荷的减小,削弱了原子核对入射粒子的作用。要考虑电子屏蔽效应,关键的问题是求出在不同碰撞参数下,入射粒子所能够感受到的核电荷的有效值。原子中不同轨道上的电子能量Ei由公式(1)给出。其中Z*为有效核电荷数,它表示在该轨道上的电子所能感受到的核电荷数;n*为有效主量子数,它与主量子数n一一对应。结合斯莱特规则可以给出不同轨道对应的Z*和n*值,具体方法参考文献[13]。
Ei=-13.6(Z*/n*)2
(1)
另外,电子在核外的运动可以被近似地看成电子在不同轨道上绕着原子核转动,沿轨道运动的电子的能量可以由公式(2)给出。通过这2个公式就可以计算出不同轨道对应的半径r和有效核电荷数Z*。
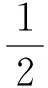
(2)
式中,r为轨道半径,e为电子电荷,ε0为真空电容率。
定义屏蔽常数S=Z-Z*。图4给出了不同轨道半径下屏蔽常数。对其进行拟合便可以得到公式(3),利用公式(3)可以得到任意半径下的屏蔽常数。
S=14.843ln(r)+442.56
(3)
对以瞄准距离b(r)入射的粒子,其感受到的有效电荷为Z*=Z-S(b)。其中S(b)由公式(3)计算得到。将该有效电荷代入到模拟程序中,即可以给出电子屏蔽对单靶核Rutherford散射的影响。图5给出考虑屏蔽效应后的散射概率,其中点划线为考虑电子屏蔽后的散射概率,实线为单靶核散射概率。可以看出考虑电子屏蔽后的散射概率与单靶核散射概率相比,在小角度范围内更小。这是由于瞄准距离大的α粒子,其有效核电荷小,故散射概率也小。
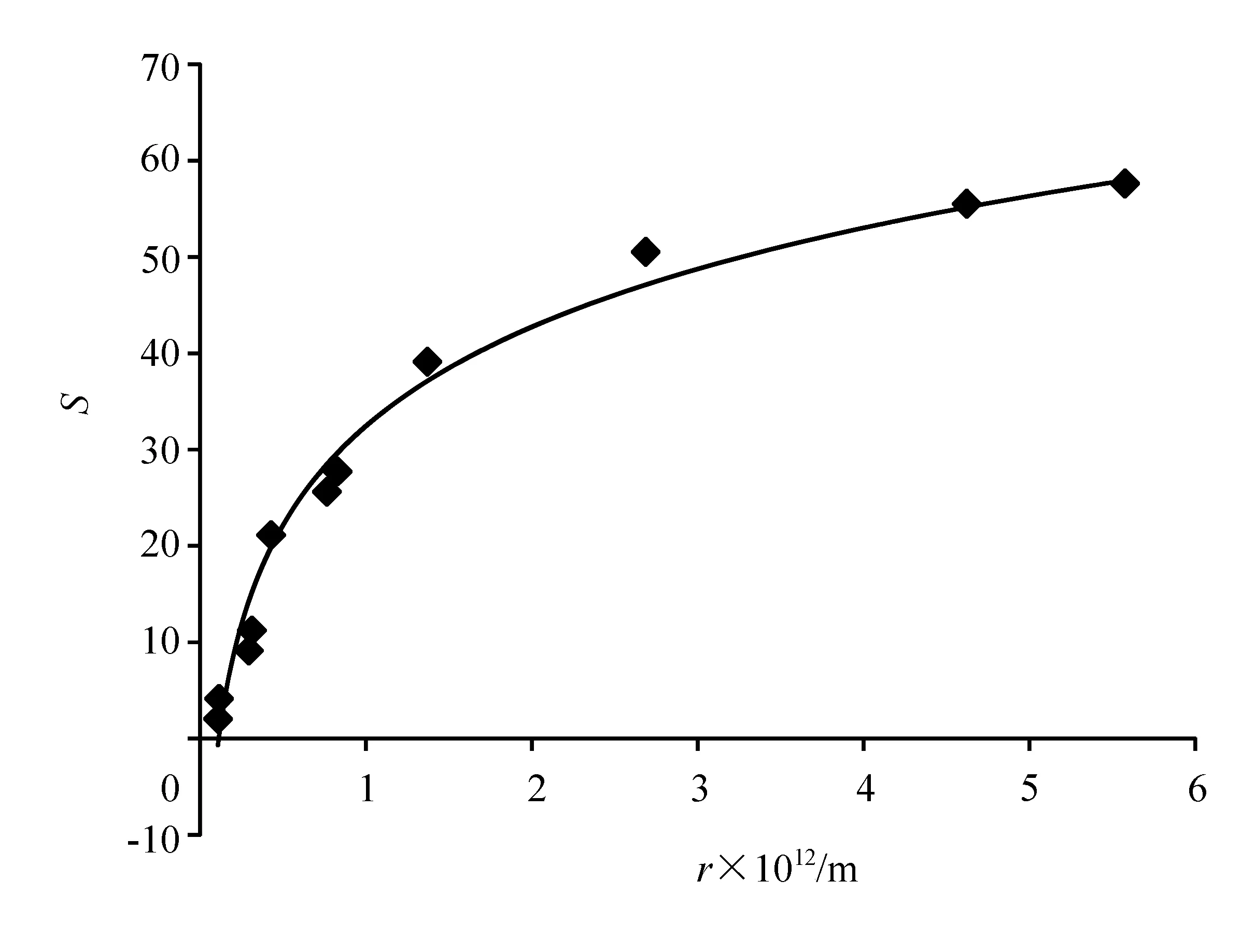
图4 屏蔽常数与轨道半径的关系曲线
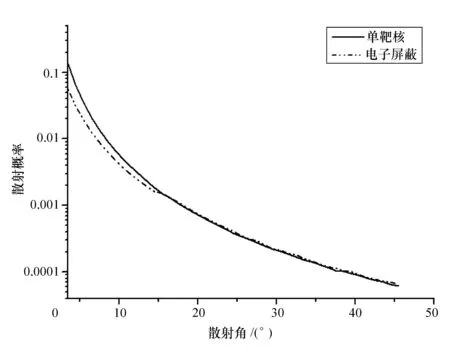
图5 屏蔽效应散射概率曲线
3.3 对比分析
上面分别讨论了多次散射及电子屏蔽的两种效应的作用机理,并讨论了它们对散射概率的影响。在图6中,分别画出多次散射、电子屏蔽及单靶核散射条件下的散射概率。可以得出:在小角度范围内,多次散射和电子屏蔽对α粒子的散射概率的影响是不同的:多次散射使α粒子的散射概率增大,而电子屏蔽导致散射概率减小,两者对散射概率的影响相反。在作用效果上,显然多次散射的作用更大,说明多次散射才是影响小角度Rutherford散射的主要因素。随着散射角的增大,多次散射对散射概率的影响先增大后减小,而屏蔽效应的影响逐渐减小。
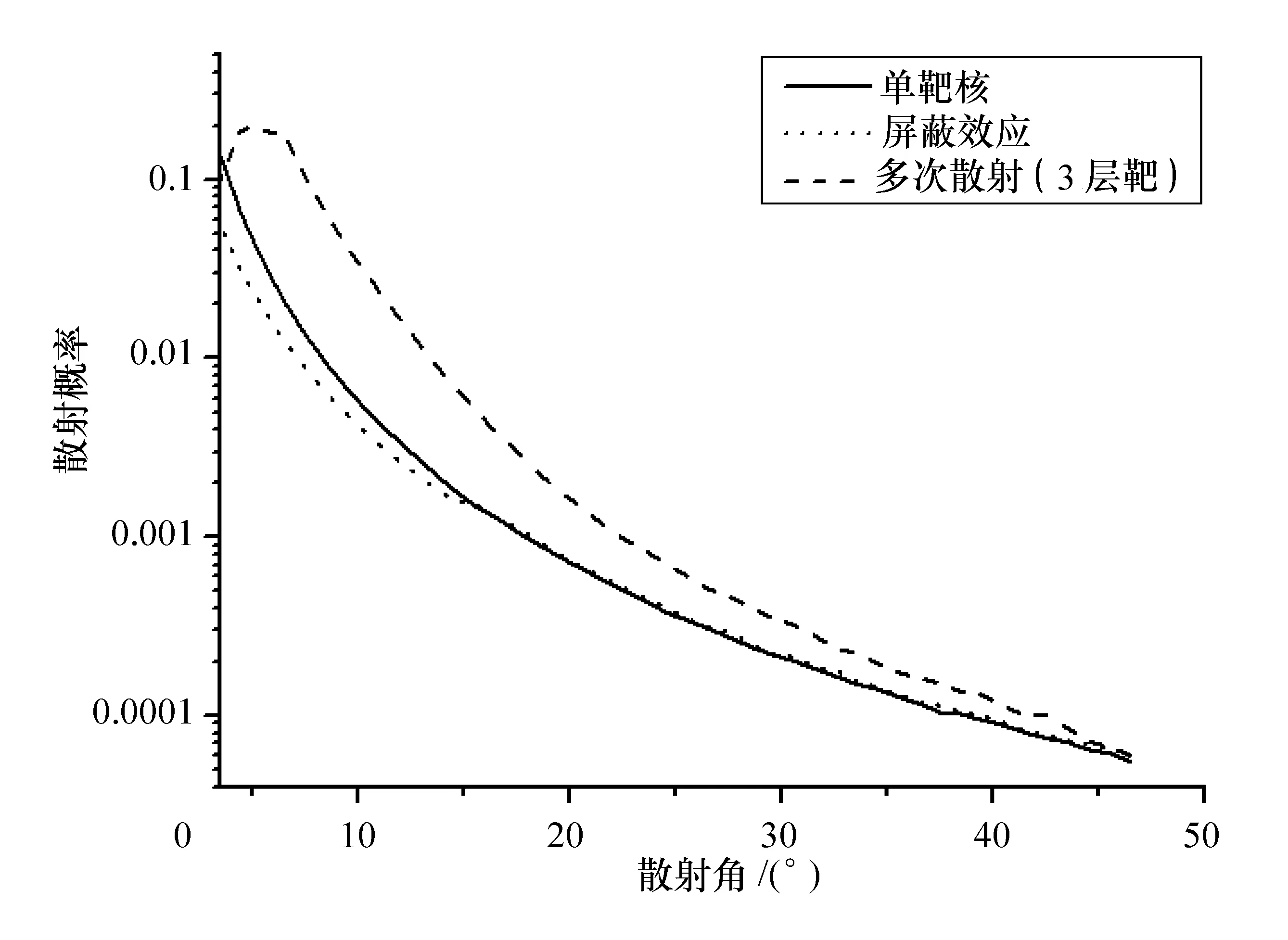
图6 两种因素对比的散射概率曲线
图7为散射概率的相对变化率曲线,散射概率的相对变化率的定义见式(4)。由图7可以看出:多次散射对散射概率的影响范围为0°~45°,而电子屏蔽对散射概率的影响范围为0°~15°;多次散射对散射概率的影响约为电子屏蔽的5倍以上。
散射概率相对变化率=

(4)
4 结语
本文以单靶核Rutherford散射的模拟为基础,建立了一套模拟多靶核Rutherford散射的方法。利用该方法研究了多次散射、靶核遮掩、电子屏蔽对Rutherford散射影响,解释了每种因素的作用机理,并经过分析对比,确定多次散射是影响小角度Rutherford散射的主要因素。
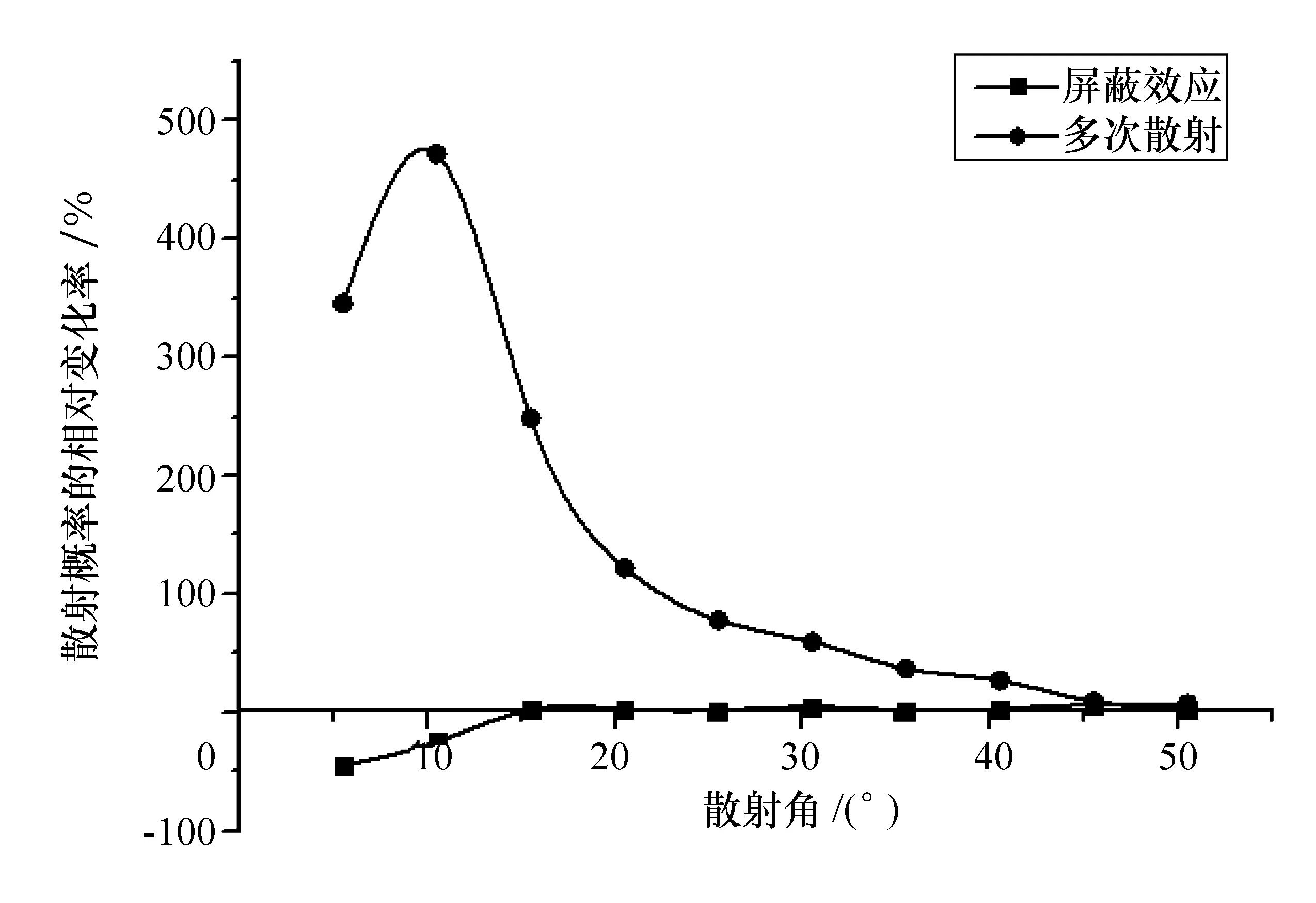
图7 散射概率的相对变化率曲线
References)
[1] 赵国庆. 卢瑟福背散射分析[J]. 理化检验:物理分册, 2002, 38(1):41-46.
[2] 刘超卓. 分析薄膜厚度与成分的卢瑟福背散射技术[J]. 理化检验:物理分册, 2010, 46(7):436-440.
[3] 师应龙, 丁晓彬, 李冀光,等. α粒子散射实验的理论模拟[J]. 大学物理, 2007, 26(5):40-43.
[4] 吴去非. 卢瑟福散射公式的有效性在小角度上的极限[J]. 大学物理, 1992, 11(2):23-24.
[5] 马晓栋, 韩锋. 关于卢瑟福散射公式中小角散射问题[J]. 新疆师范大学学报(自然科学版), 1998(1):20-25.
[6] 任玉安. 卢瑟福散射公式在小角度上的有效性[J]. 食品科学技术学报, 1996(1):98-101.
[7] 李佳惠,刘波,李小琪,等. 单靶核Rutherford散射的模拟与优化[J].科技展望,2016, 26(2):115-117.
[8] 魏东平,朱连章,于广斌.C程序设计语言[M].北京:电子工业出版社,2009.
[9] 杨福家. 原子物理学[M]. 4版.北京:高等教育出版社, 2008.
[10] 褚圣麟.原子物理学[M].北京:高等教育出版社, 1979.
[11] 尹建武. 卢瑟福散射公式的几种推导方法[J]. 黄冈师范学院学报, 2003, 23(3):31-34.
[12] 刘宇, 唐昌建. 卢瑟福散射及其计算机模拟[J]. 原子能科学技术, 2010, 44(11):1281-1286.
[13] 李凤东. 屏蔽效应与斯莱特规则的应用[J]. 电大理工, 2010(4):42-43.
Simulation and research of small angle Rutherford scattering
Zhou Wei, Li Cong, Li Jiahui
(College of Science , China University of Petroleum, Qingdao 266580, China)
Based on the computer simulation program of the single target Rutherford scattering, a simulation program of multiple target Rutherford scattering is compiled. The factors that affect the applicability of the Rutherford scattering formula such as multiple scattering, target nucleus covering, electron shielding, etc., are intuitively studied by using the multiple target simulation program. The physical images of the small angle Rutherford scattering can be understood and analyzed better. By comparing and analyzing the different factors, the main factors that influence the small angle Rutherford scattering are found.
Rutherford scattering; computer simulation; multiple scattering; target nucleus covering; electron shielding
O562.5
A
1002-4956(2017)10-0033-04
10.16791/j.cnki.sjg.2017.10.010
2017-04-27修改日期2017-06-02
山东省自然科学基金项目(BS2015SF013);中国石油大学(华东)青年教改项目(QN201526);中国石油大学(华东)大学生创新创业项目(20161392)
周伟(1982—),男,山东济宁,博士,讲师,研究方向为粒子物理和原子核物理.
E-mail:zhouwei@upc.edu.cn

