基于改进差分进化算法的煤矿井下逃生路径优化
赵海军
(阳泉市南庄煤炭集团有限责任公司,山西 阳泉 045001)
基于改进差分进化算法的煤矿井下逃生路径优化
赵海军
(阳泉市南庄煤炭集团有限责任公司,山西 阳泉 045001)
为了减少矿难中的损失,提高被困人员的幸存概率,基于改进差分进化算法,提出一种煤矿井下逃生路径优化方法。分析了影响逃生的六个影响因素,并根据这些因素建立了地下巷道权值计算模型。通过设计混合变异策略和参数自适应机制来提高差分进化算法的搜索效率,从而快速寻找最优逃生路径。实验结果表明,所提方法能够有效的找到最优逃生路径及其他次优可选路径。
优化; 逃生;巷道;差分进化
在采矿中,水、火、瓦斯以及其他自然灾害经常发生,灾害对矿山的安全生产有着重大影响。统计显示,我国煤矿行业伤亡事故最为严重。从2001年到2010年就有86 000多人死于煤矿事故,占采矿事故死亡人数的85%。根据2006年到2008年的统计数据显示,在我国高危行业中,煤矿事故率和死亡率分别占21.3%和28.5%,位列工矿业首位[1]。
当矿难发生后,如何确定一条最佳的避灾救援路线,指导受灾人员安全撤离,以及安排救援人员及时展开有效的救援,最大程度的降低事故影响至关重要。为了确定最佳逃生路径,国内外学者提出了很多算法。例如,文献[2-4]使用的改进Dijskstra算法,根据矿井巷道平面网络的运行效率,通过限制搜索方向和范围在扇形区域内寻找最优路径,并根据用户给出的源点和目的点,以及搜索的扇形角度寻找最优路径,从而提高效率。然而,Dijskstra算法具有三点不足之处:1)由于Dijskstra算法需要遍历网络中的所有节点,所以需要很大的计算代价;2)Dijskstra算法只能寻找到最优路径,但在很多情况下,需要得到多条符合要求的次优路径;3)Dijskstra算法为静态算法,当有状态变化时,算法需要重新计算[2-4]。
差分进化算法(DE)[5]作为一种随机性算法,是进化算法中最简单而高效的算法。DE算法通过模仿生物群体内个体间的合作产生的群体智能实现对优化问题的求解,具有能够记忆个体最优解,种群内信息共享及易于其他算法结合的特点[6],在电力系统、化学工程、公交调度及生物信息学等领域得到了广泛应用[7],尤其对大规模网络最优路径优化问题极其有效。
本文分析人员逃生过程中巷道环境和安全性两个方面的因素,并分析各个因素的影响权值,建立权值数学模型,并根据人员所在事故源点与设置的安全目标点,求取两点间的所有连通路径; 其次,对传统差分进化算法的变异策略和参数选择机制进行了改进,引入混合变异策略和参数自适应机制,从而提高算法的搜索效率。最后利用所提出的改进差分进化算法决策出最优逃生路径和其他次优可选路径。
1 巷道权值计算模型
1.1 巷道当量长度计算
影响人员通过巷道的因素通常有六类: 巷道类型、风速、巷道坡度、颗粒浓度、拥挤度和其他与矿难相关的特殊因素。这些因素都影响着人员的逃生速度,他们可以加快或减缓逃生速度v。上述因素均可转化为巷道当量长度,且逃生速度v越小则当量长度越长,这些当量长度即为整个巷道网络图G的权值:
li=(kti·kwi·kgi·kvi·kmi·kdi)lri
(1)
式中:lri表示第i条巷道的实际长度,li表示第i条巷道的当量长度;kti、kwi、kgi、kvi、kmi和kdi分别表示第i条巷道的巷道类型影响系数、风速影响系数、巷道坡度影响系数、巷道颗粒浓度影响系数、巷道拥挤度影响系数和其他特殊情况的影响系数。
在巷道类型系数的影响下,人员的逃生速度v等于v0/kti,其中v0为人员正常步行速度。由于各权值系数各自独立,因此在他们的共同影响下,逃生速度v为li/v。
1)巷道类型影响系数
地下巷道通常分为工作面、运输胶带巷、联络巷、铁路巷、漏风分支和通风井,其中,漏风分支和通风井无法通过。这些都影响着人员的逃生速度,例如,在铁路巷中,逃生速度则与交通速度有关。巷道类型的影响系数:
(2)
式中:vvehicle为交通工具的速度,m/s。
2) 风速影响系数
采矿网络本身就是一个完整的通风系统,一般总回流车道的风速很大,风速可能影响人员的逃生速度。风速的影响程度通常与道路的实际长度成正比。假设人员的行走能力为P0,则逆风行走时
P0=Fv0=(F+Fw)v.
(3)
式中:F为人行走所作的力,N;v0为人的正常行走速度,m/s;Fw为风力,N;v为人受风影响后的行走速度,m/s。
假设人为一个长方形的物体,则
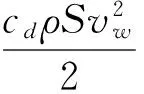
(4)
式中:cd为阻力系数,经验表明其与雷诺数有关;ρ为气体密度,kg/m3;S为人体与风的接触面,m2;vw为此条路上的风速,m/s。根据式(3)和(4)有
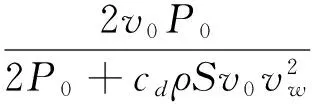
(5)
则逆风行走时的风速影响系数为
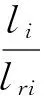
(6)
同理可得,顺风行驶时的风速影响系数为
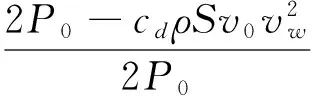
(7)
但当风速很大时,式(7)不适用。
3) 巷道坡度影响系数
巷道的坡度影响人员的行走速度,坡度越大,阻力越大。由此可得上坡时
P0=Fv0=mgvsinθicosθi.
(8)
式中:m为人体的标准质量,kg;g为重力加速度,m/s2;θi为当前巷道的坡度角,°; 假设人员通过斜坡巷道时的速度始终为v0,则上坡时的影响系数为
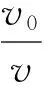
(9)
4) 巷道颗粒浓度影响系数
巷道颗粒浓度主要包括巷道能见度和气体临界层与地面的高度,这些都严重影响着人员的逃生速度,其影响系数为
kvi=(1+αh+Lr).
(10)
式中:αh为气体临界层与地面的高度的影响系数,Lr是能见度影响系数。αh和Lr经验取值分别如表1和表2所示。

表1 αh取值

表2 Lr取值
5)巷道拥挤度影响系数
人群的密集度从某种程度上影响着行走速度。本文采用Thompson[8]提出的人群密集度影响的行走速度模型:
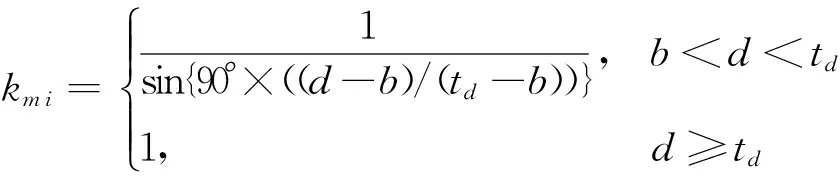
(11)
式中:d为人与人之间的距离,td表示表示移动约束区间的上限,b表示水平方向上行走的人数。
6) 其他与矿难相关的特殊因素影响系数
为了简化各种巷道灾害的数学模型,本文使用kdi,kdi∈(1,+∞)表示其他特殊因素的影响系数,其中1表示巷道正常,没有发生矿难,+∞表示此巷道不可通过。例如,严重滑坡,高温以及水淹没了巷道等情况都导致巷道不可通过。
1.2 巷道权值规范化
根据2.1的分析,巷道的当量长度范围为[0,+∞),其中+∞表示巷道不可通过。为了方面数据处理,根据式(12)将所有数据映射到(0,1]中:

(12)
式中:min(l)表示所有巷道的最小当量长度m,max(l)表示所有巷道的最大当量长度m(不包括长度值+∞)。式(12)表明wi越接近于0,越容易通过。当等于1时,表明巷道不同通过。
通过上述的权值规范化,可以根据所提的改进差分进化算法来寻找最优逃生路径。
2 基于改进差分进化算法的逃生路径优化
本文提出一种通过改进差分进化算法的变异策略及加入参数自适应机制来提高算法的搜索效率,从而快速有效的求出最优逃生路径及其他次最优路径。
2.1 基本差分进化算法
DE算法通过种群内个体间的合作与竞争来实现对优化问题的求解,其本质是一种基于实数编码的具有保优思想的贪婪遗传算法。与其他进化算法一样,DE算法也包括初始化、变异、交叉和选择四个操作。算法首先在定义域范围内随机生成初始种群,然后通过变异和交叉操作产生新个体,最后通过选择操作决定新个体是否能成功进入下一代。假设目标函数为f(x),x=(x1,x2,…,xN)∈RN,可行域为D,则具体步骤如下:
1) 初始化
在目标问题的可行解空间D中随机初始化种群P=[x1,x2,…,xNp],Np为种群规模,xi=[xi,1,xi,2,…,xi,N]表示目标问题的解,N为目标问题的维数。
2) 变异
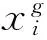
).
(13)

(14)
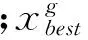
3) 交叉
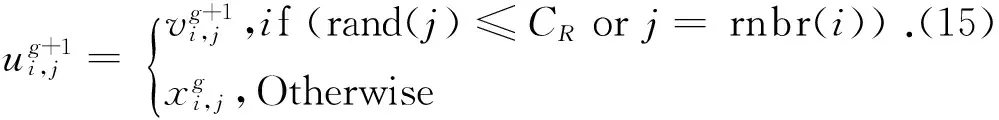
4) 选择
(16)
式中:f为目标函数。
2.2 改进变异策略
众所周知,DE/best/1在求解过程中促使种群中的每个个体向当前种群中的最优个体收敛,因此对单模问题和一些简单的多模问题求解时具有很快的收敛速度,但是对于一些高维多模问题,很容易陷入局部最优而出现早熟收敛。DE/rand/1是一种最常用的变异策略,他能够很好的维持种群的多样性,全局搜索能力较强,但是局部搜索能力较弱,导致后期收敛速度很慢。为了平衡DE算法的全局搜索能力和收敛速度,本文提出一种改进变异策略,将DE/best/1和DE/rand/1混合使用。
在群体初始化过程中,将DE/best/1和DE/rand/1随机分配给每个个体,且在整个进化过程中保持不变,设Mi为个体Xi的变异策略,则
(17)
式中:randi为[0,1]之间的随机数。
2.3 参数自适应策略
相关文献研究表明,DE算法的性能高度依赖于控制参数(如种群规模Np、增益常数F和交叉概率CR)[8]。由于不同的优化问题有着不同的数学特性,不恰当的参数不仅会导致算法计算代价较大(如函数评价次数)、收敛速度较慢,而且极易趋于早熟收敛而陷于局部最优解。本文提出一种简单的参数自适应策略来动态调整参数F和CR。
(18)
式中:N(0.5,0.1)为均值为0.5,标准误差为0.1的正态分布随机数。式(18)表明,如果当前的CR能够产生较优的新个体,则在下一代时继续保值不变,否则重新生成CR。
对于参数F,根据均值为0.5,标准误差为0.3的正态分布随机数生成,即N(0.5,0.3)。
3 实验
为了验证模型和所提算法的有效性,通过文献[9]的实例来进行求解分析,图2给出了矿井的网络拓扑图。实验中,模型中的参数设置如3所示。算法参数设置为CR=0.5,F=0.5。表4给出了地下巷道网络(图1)的部分数据和权重值。

表3 基本参数设置
通过所提出的改进差分进化算法,对图1所示的矿井网络拓扑进行优化求取最优路线及次优路线。表5给出了算法5次独立运行中得出的最优路线和两条次优可选路线。从表中可以看出,最优路线在节点82和节点1之间,最优路线在5次运行中均为(83,84,82,80,77,76,74,63,57,55,45,1),比较稳定,其他两条次优可选路线不稳定,在5次算法运行中得出的结果不同。图1中绘制出了算法第一次运行的结果,其中红色路线为最优路线,绿色为次优路线1,蓝色为次优路线2。

表4 地下巷道网络的部分数据和权重值
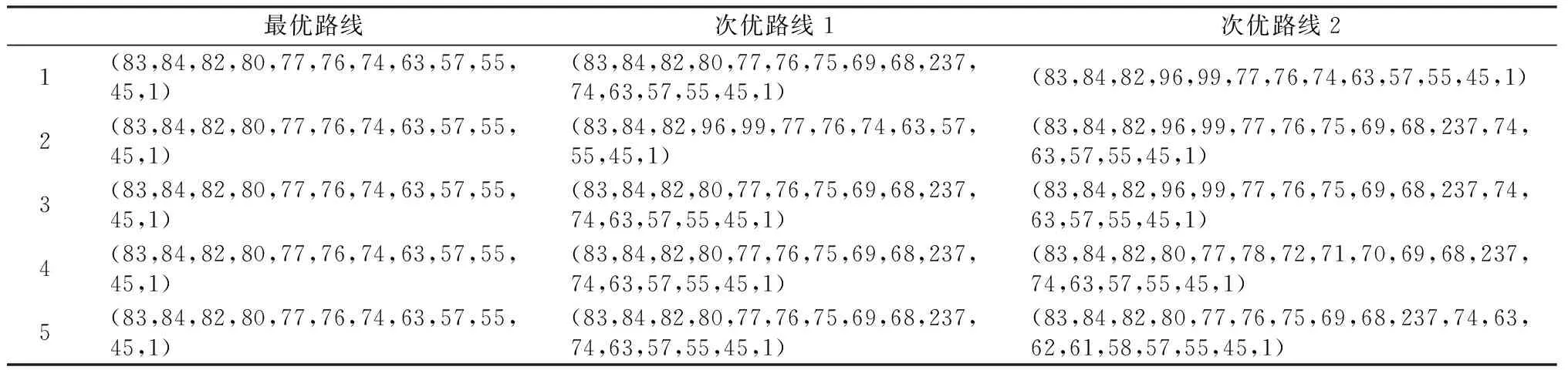
表5 算法5次独立运行的结果
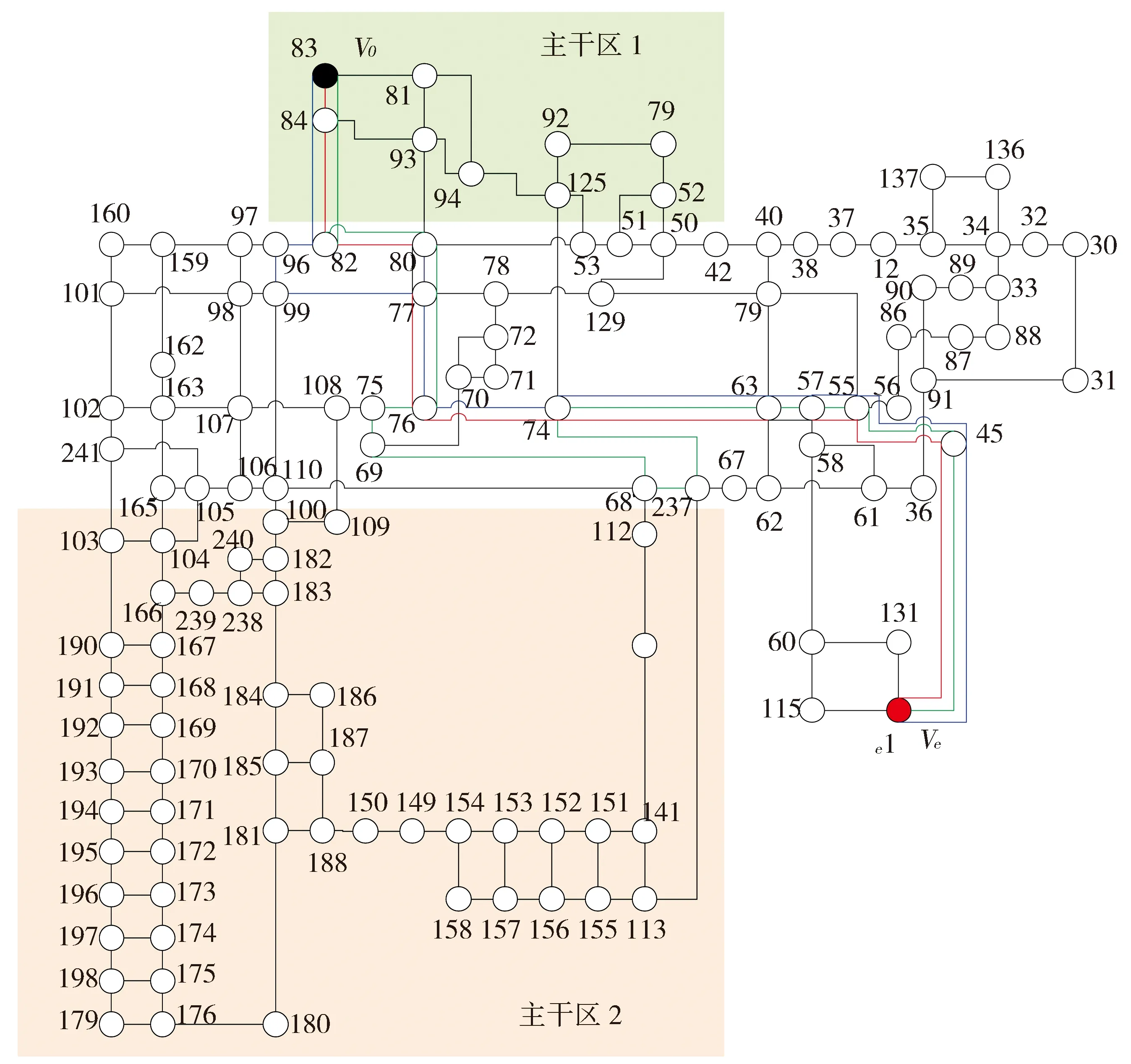
图1 地下矿井网络拓扑Fig.1 Network topology of underground mine
4 结束语
本文首先通过对地下矿井逃生中的各种影响因素进行了分析,建立了巷道权值模型。其次,提出一种改进差分进化算法快速有效的求解逃生路径,在改进差分进化算法中,通过一种混合变异策略及参数自适应机制来提高算法的搜索效率和收敛速度。最后通过一个实例来验证了所提算法的有效性,实验结果表明,所提算法能够快速稳定的求得最优逃生路径及其他次优可选路径。
[1] 杨大明.煤矿井下紧急避险系统的建设与发展[J].煤炭科学技术,2010,38(11):6-9.
YANG Daming.Construction and Development of Emergency Refuge System in Underground Mine[J].Coal Science and Technology,2010,38(11):6-9.
[2] 李舒伶.井下最佳避灾路线确定[J].辽宁工程技术大学学报,1999,18(1):27-29.
LI Shuling.The Confirmation of the Best Route for Evading Accident Under the Pit[J].Journal of Liao Ning Technical University,1999,18(1):27-29.
[3] 侯运炳,夏兴,闫旭.基于矿井地理网络模型的最短路径改进算法[J].2011,39(2):103-105.
HOU Yunbing,XIA Xing,YAN Xu.Improved Shortest Path Algorithm Based on Mine Geographic Network Model[J].Coal Science and Technology,2011,39(2):103-105.
[4] Jalali S E,Noroozi M.Determination of the Optimal Escape Routes of Underground Mine Networks in Emergency Cases[J].Safety Science,2009,47(8):1077-1082.
[5] Storn R,Price K.Differential Evolution-A Simple and Efficient Heuristic for Global Optimization Over Continuous Spaces[J].Journal of Global Optimization,1997,11(4):341-359.
[6] 周晓根,张贵军,郝小虎.局部抽象凸区域剖分差分进化算法[J].自动化学报,2015,41(7):1315-1327.
ZHOU Xiagen,ZHANG Guijun,HAO Xiaohu.Differential Evolution Algorithm with Local Abstract Convex Region Partition[J].Acta Automatica Sinica,2015,41(7):1315-1327.
[7] Das S,Suganthan P N.Differential Evolution:a Survey of the State-of-the-art[J].IE Transactions on Evolutionary Computation,2011,15(1):4-31.
[8] Thompson P,Marehant E.A Computer Model for the Evacuation of Large Building Populations[J].Fire Safety Journal,1995,24(2):131-148.
[9] Stutzle T,Hoos H H.Max-Min Ant System[J].Future Generation Computer Systems,2000,16(8):889-914.
OptimizationofEscapeRouteinCoalMineBasedonImprovedDifferentialEvolutionAlgorithm
ZHAOHaijun
(YangquanNanzhuangCoalGroupCo.,Ltd.,Yangquan045001,China)
To reduce the loss and improve the surviving probability of trapped miners in mine disasters, a new escape route optimization method for mines is proposed with an improved differential evolution algorithm. Six influential factors are analyzed to build a weight calculation model. Then, a hybrid mutation strategy and parameter adaptive mechanism are used to improve the searching efficiency of the differential evolution algorithms in order to find the optimal escape route quickly.The results show that the proposed method could effectively find the optimal route and alternative routes.
optimization;escape;roadway;differential evolution
1672-5050(2017)01-0051-05
10.3919/j.cnki.issn1672-5050sxmt.2017.02.016
2016-05-19
赵海军(1970-),男,山西阳泉人,大学本科,工程师,从事矿井通风安全研究。
TP18
A
(编辑:薄小玲)

