南昌井水位对远震的同震响应分析
牛在坡查小惠
(江西省地震局,江西南昌 360039)
南昌井水位对远震的同震响应分析
牛在坡,查小惠
(江西省地震局,江西南昌 360039)
通过对2001—2008年间139次震例数字化资料的总结,定性分析了南昌井水位资料对强远震的响应情况,并采用二阶回归方法对模型进行优化和定量分析。研究认为:南昌井水位资料对强远震响应较好,同震响应幅度与震级、震中距综合相关,响应距离随震级增加而增加,但在各震级档中均存在距离上限。
南昌井水位;同震响应特征;量化分析模型
0 引言
实践证明地下流体对于地震的异常响应,在整个地震前兆观测体系中的表现是比较明显的[1],尤其水位的同震效应,其异常幅度、分布广度都是比较突出的。但不同井孔的灵敏度、响应形式等不尽相同,这与井孔的地质构造、围岩(含水层)条件、以及震级、震中距等多种因素有关。近年来,不少学者对此进行了广泛研究,涉及到响应特征、机理、后效预报等多方面。比如,黄辅琼等[2]在1999年台湾集集地震后首先从空间上分析了这些变化与中国大陆构造的关系,并将其应用到了地震的地点预报实践中;随后付虹等[3]对云南地区的观测井进行了详细的清理,并形成了云南地区利用响应预报地震地点的区域性方法。杨竹转[4]等对云南思茅井水位进行了同震阶跃与地震震级、震中距的统计分析,得到了井水位响应幅度与震级及震中距之间的定量化关系式,其结果大致与国际上针对单一井孔对多个地震响应的研究结果一致:井水位响应幅度随震级增大而增大,随震中距增大而减小,其关系基本为线性[5]。其响应变化的形态比较单一,或总是下降,或总是上升,不随地震的不同而变化。基于这种变化特征,国际上比较一致的观点认为是地震造成的地面运动导致了水位的变化。
针对上述已经取得的研究成果,本文将以南昌井为重点,研究井水位对地震响应的定量化特征,加深对南昌井水位资料的认识,同时检验上述结论的普适性。
1 井孔背景概况
南昌地震台水位观测井位于南昌市郊梅岭山麓,地理坐标(28.7675°N,115.8002°E),海拔高程68m。
地质构造方面,该井位于鄱阳盆地边缘、赣江断裂带(湖口-吉安断裂)北东向断裂束附近。赣江断裂是江西省境内一条主要构造带,自北向南贯穿全省,地貌上是一条醒目的低谷带,与赣江流向基本一致,南昌井附近断裂走向主要呈NE40°~ 60°,以压性、压扭性活动为主[6]。 断裂西侧为丘陵山地,岩层岩性主要有混合花岗岩(Mr2
2)、均质渗透混合岩(Ptbn)和花岗闪长岩(ro2
2),为元古代雪峰晚期产物。断裂东侧为第四系中更新统残积层(Q2el)河流阶地、平原,地势低平,见图1。
观测井孔于1979年钻成,孔深72.92m,钻探揭露的围岩为花岗片麻岩。井孔位于山前坡地,井孔位置较低,地下水具有承压性。属浅表、冷水(年均水温19°左右,随季节变化)、自流井。
2 水位及地震资料
南昌井水位观测仪器1984年以前使用红旗一型,观测精度为0.5cm,1985年改用Sw40-1型,观测精度为0.1cm,2001年9月增上 LN-3型数字化观测仪器,精度0.1cm,经比较,模拟记录与数字记录动态变化基本一致[7],均表现出较明显的夏高冬低年变形态,可记录每日双峰双谷的固体潮波形,及水震波、水位阶等。由于机构撤销等历史原因,目前仅有1989年以来的连续水位资料(图2)。
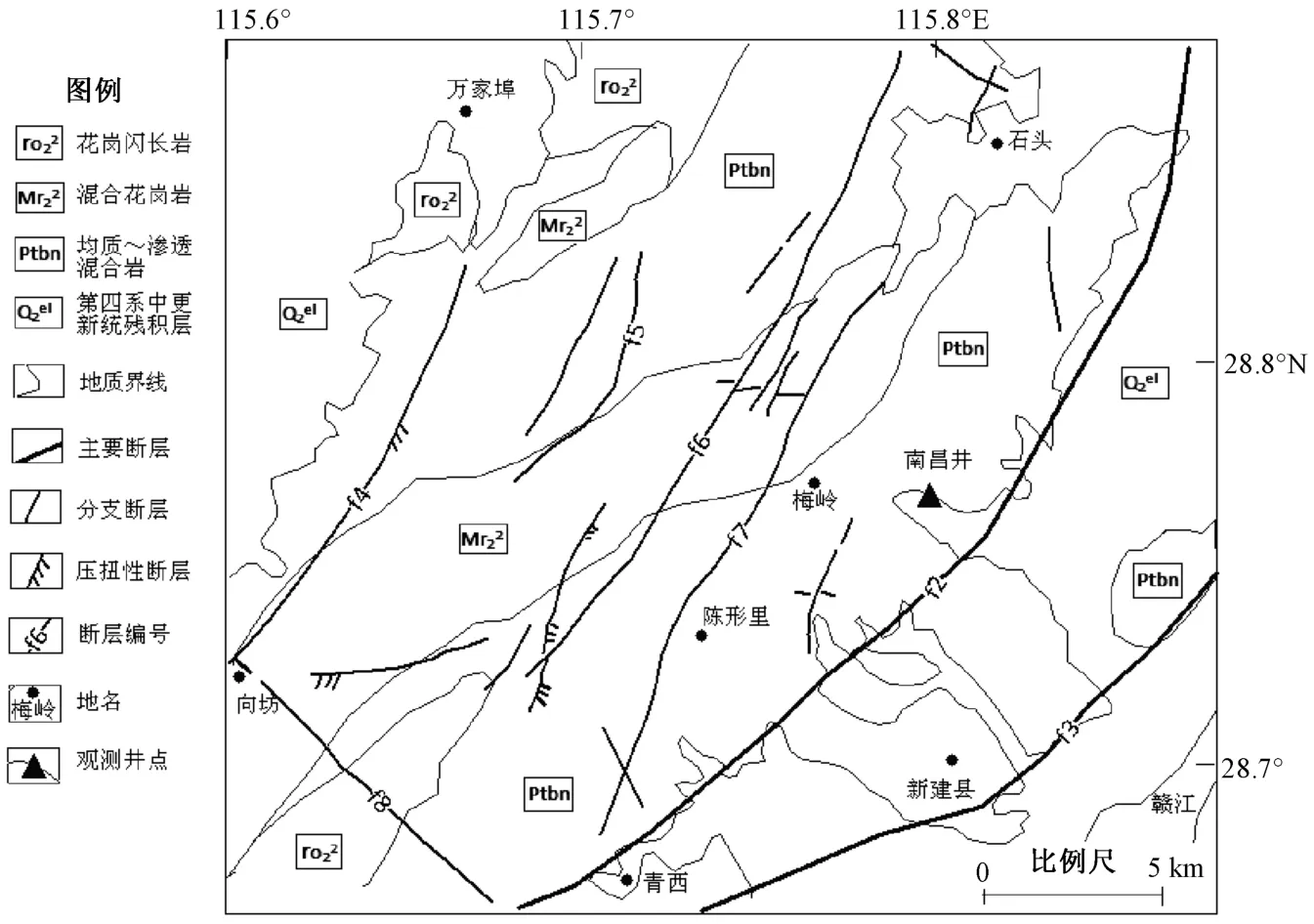
图1 南昌井地质简图(据江西地质区调大队1∶20万地质图绘制)Fig.1 Geological diagram of Nanchang well
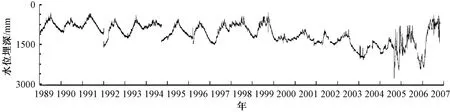
图2 南昌井水位原始整点值图Fig.2 The integral point value of Nanchang water level
水位同震现象并不罕见,但同一口井对于时间、地点、震级各不相同的地震的同震研究,尚属鲜见,本文尝试进行整理并归纳同震特征。南昌井附近地质构造单元相对稳定,地震活动稀少,1970年有仪器记录以来,台站50km范围内发生ML1.0以上地震仅13次(地震目录资料来源于中国地震局台网中心,下同),最大ML3.2级,基本不存在背景扰动,为异常分析提供了良好的基础,见图3。
3 强震同震响应分析
南昌井水位记录,对周边强震有较好的同震反应,在1990年以来的139次MS7以上地震中(4000km内,下同),有13次明显的同震阶跃响应(另有一次脉冲式响应),如1994年9月16日台湾海峡MS7.3地震、1999年9月21日台湾南投MS7.6强震群,水位时值振幅分别达到59cm和31cm,在记录中形成大幅阶跃,前者更是由于瞬间振幅过大、记录笔靠死,造成资料中断。同震响应表现出距离性,总体上随震级增加,响应距离增大,但超过4000km后,未发现响应震例。同时,在统计资料范围内,表现出较低震级具有响应距离上限(无响应的最小距离)的现象,有响应的震中距一般小于该上限值,见表1、图4。
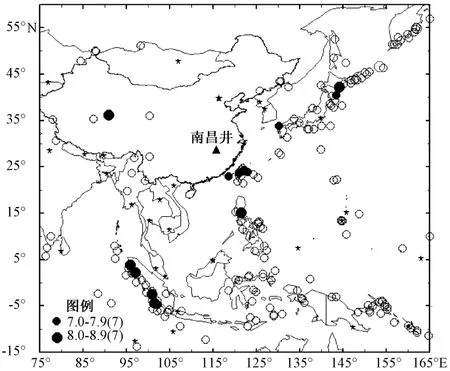
图3 南昌井有响应的远震分布(实心圈)Fig.3 Distribution of distant earthquake response to Nanchang well
数字化资料由于动态范围大,能完整记录地震前后的变化情况,且日志记录相对齐全,有助于甄别干扰,故选用南昌井水位数字化资料进行研究,时段为2001年9月至2007年12月。
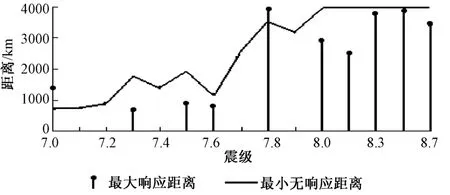
图4 不同震级同震响应距离关系Fig.4 Coseismic response distance relationship in different magnitude
采用数字化水位时值记录,通过对研究时段内全部52次MS7以上强震的逐一对比筛选,确认其中9次存在明显同震水位阶变化(表2、图5)、2次在分钟值上有同震脉冲现象,但2005年8月16日与日本宫城MS7.1地震同期产生的大幅水位变化,经核实属于因水井气氡脱气装置改造实验[8],使用了步进电机抽水造成,故分析时剔除。
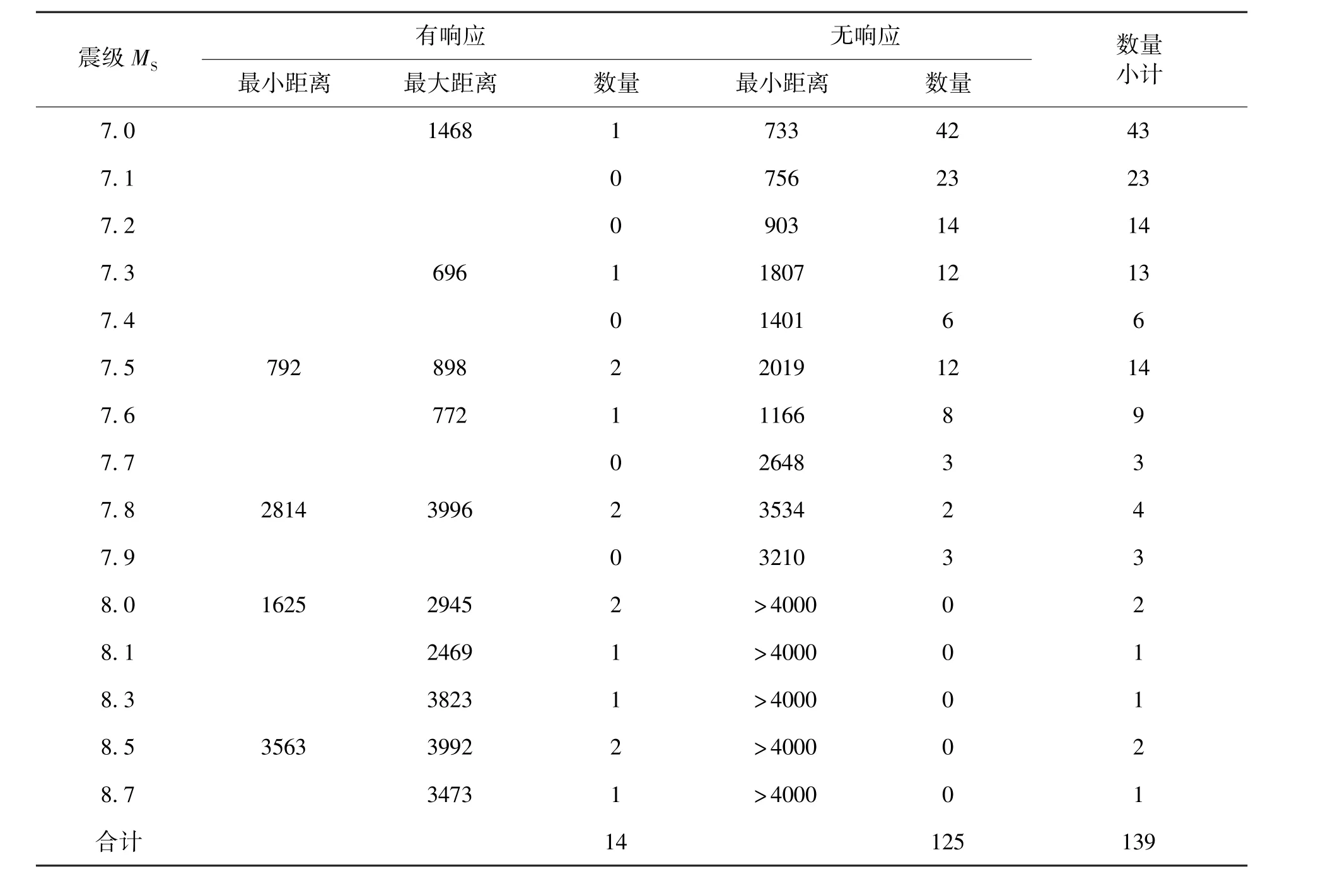
表1 远场强震影响距离统计(单位:km)Tab.1 Statistics of influence distance by the far field earthquake
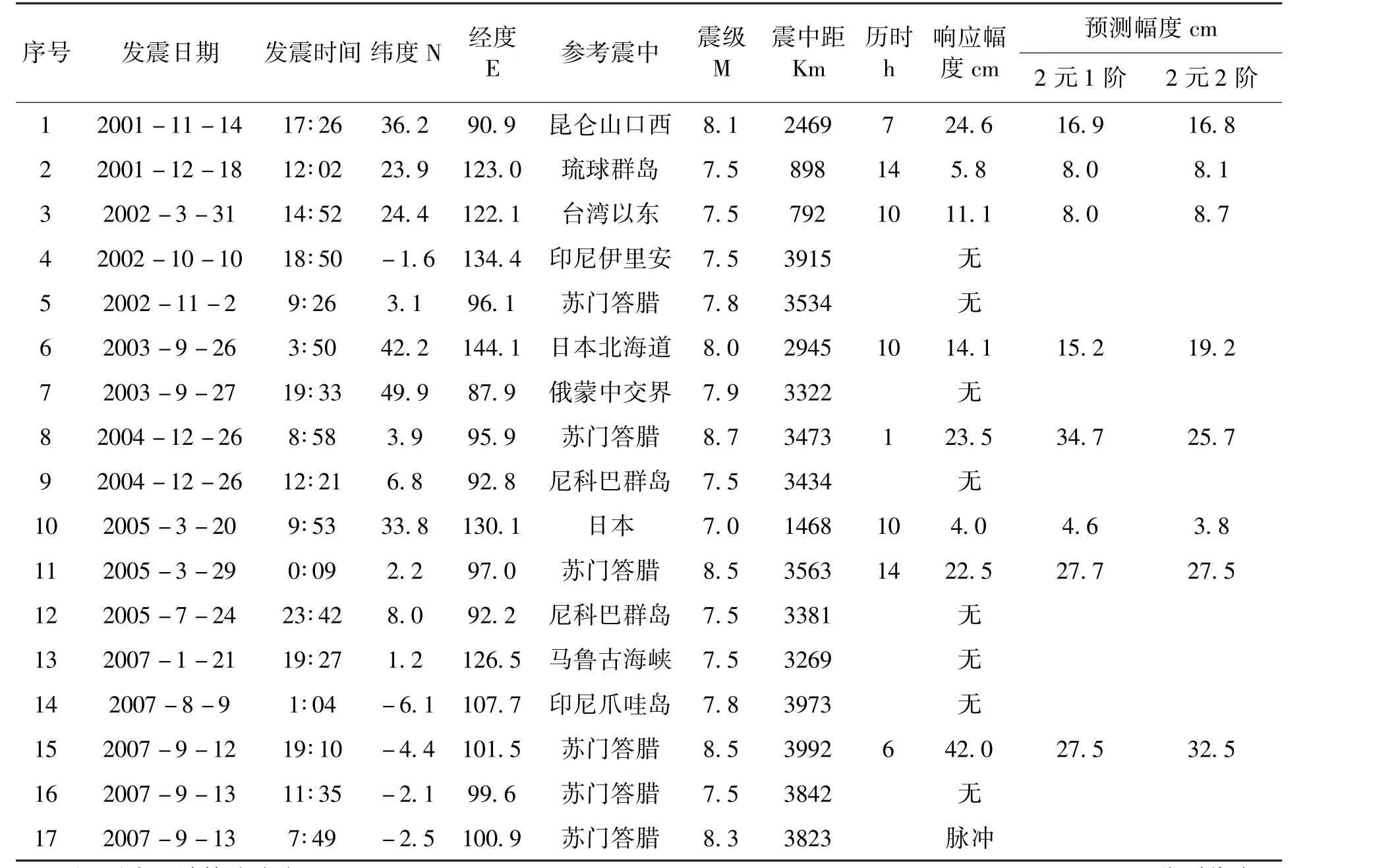
表2 南昌井水位阶跃及7.5级以上地震目录Tab.2 Water level jump of Nanchang and the M≥7.5 earthquakes catalogue well water
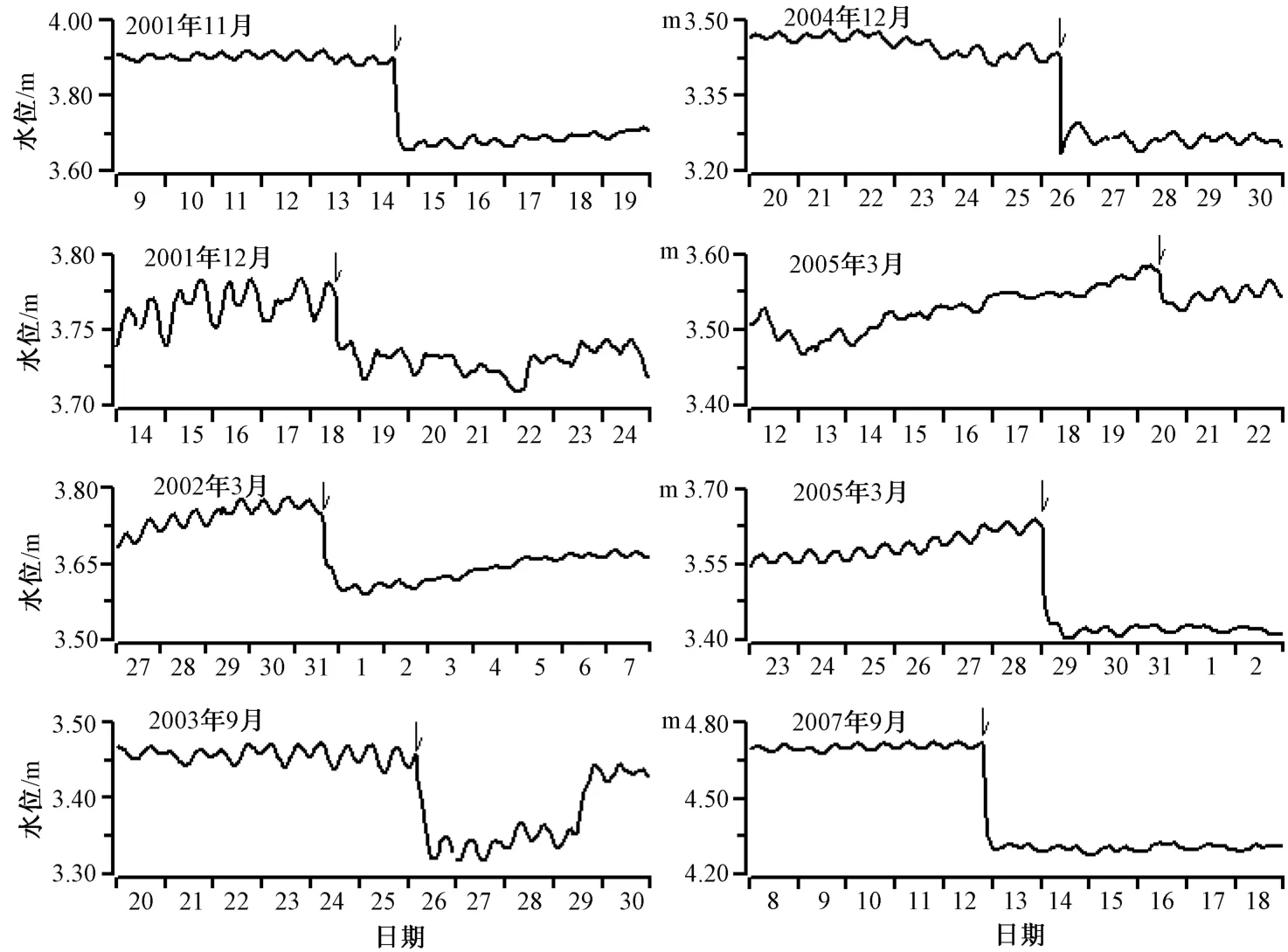
图5 水位同震阶跃图(时值)Fig.5 Coseismic water level step
综观各次震例,有以下发现:
(1)同震形成的阶跃方向均为向下,即水位值下降,幅值在4~42cm之间,在震后1~14小时达到最低值后回升,平均历时9小时。震后水位恢复通常较为缓慢,回升到震前水平从3天到数周不等。
(2)同震震例中,7次震级在MS7.5级以上,仅1次为7.5级以下,且距离相对较近、振幅较小(1468km、4cm),水位阶跃幅度与震级总体呈正相关。
(3)对全部16次MS7.5以上地震的统计中,MS8以上均有反应(阶跃或脉冲,共6次),MS7.5~7.9则表现出明显的距离性,形成水位阶跃的2次地震为近震(<1000km),8次无响应震例均超过3200km,水位变化明显受距离影响(表2)。
(4)引起水位阶跃的地震分布在井点的各个方向,如日本、台湾、苏门答腊、新疆等,水位变化幅值、方向等与地震位置无关。
(5)水位阶跃存在“钝化”现象,即对首震响应出现阶跃变化后,灵敏性有所下降,不再对短期内发生的强震产生阶跃响应,比较突出的例子是2007年9月12日苏门答腊MS8.5地震造成南昌井水位下降42cm后,次日发生的MS8.3地震仅在分钟值上形成不到1cm的脉冲(水震波),与该井表现出的响应特性明显不符。
4 量化分析及模型优化
由前述可知,南昌井水位同震阶跃变化与强震震级、震中距有关,进一步进行量化分析,据国内外研究[4-5],水位变化幅度与震级、震中距统计关系一般形式为:
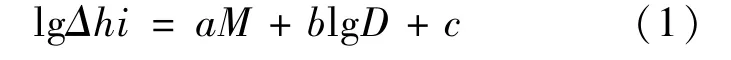
式中,Δhi为水位变化的幅值,单位为cm;M为面波震级;a,b,c为常数;D为震中距。
以水位响应幅度(表2中响应幅度有数值部分,由最小二乘原理知,与排列顺序无关)为因变量,以震级、震中距为自变量,进行二元回归计算,得到南昌井水位强震同震响应关系式:
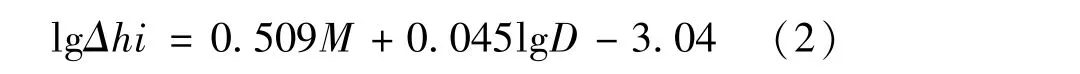
F 检验值为 12.3,在 0.05 置信度上 > F0(5.79),达到显著水平。 复相关系数为 0.83,离回归平方和仅0.14,回归计算效果较好。
由式(2)可知,水位变化幅度与震级呈正相关,但震中距的影响,对于南昌井却并不明显(系数接近0)。产生这种现象的直接原因是参与计算的源数据中本身存在矛盾性,如2007年苏门答腊MS8.5地震震中距最大,但阶跃幅度也最大;最大地震是MS8.7,但其变幅却小于MS8.1。 而深层原因是:水位响应幅度与震级、震中距虽然总体上满足上述二元线性模型的统计关系,但由于地震的影响作用可能还受到震源深度、力学机制、传播介质、以及井孔本身状态等多方面复杂因素的影响,实际情况并不遵循理想化的简单线性关系。受资料获取手段的限制,我们无法得到真实的各类影响因素值,但可通过对模型的修正改善拟合关系,笔者对此进行了初步尝试。
在保证公式(1)中两个自变元(解释量)对因变量物理意义的前提下,采用增加高阶多项式回归元的方法,可提高拟合精度。分别进行了二元二阶、二元三阶、及单独增加震级(M2阶)或震中距(D2阶)阶数的试验性计算,得到结果见表3。从复相关系数、离回归平方和等主要参数看,阶数越高效果越好,但由于样本数有限,本例中F0值随阶数升高迅速上升,三阶无法通过检验。经比较,发现二元二阶模型较原始二元一阶模型因变量标准差和偏离算术和基本持平,而复相关系数提高6%、离回归(残差)平方和及预测最大偏离值(带方向)分别下降28.6%和33.6%,拟合精度上升、误差明显减小(图6、表3),且在0.1置信度上>F0(5.34),通过 F 检验。 从预测幅度来看(表2),二元二阶较二元一阶模型更接近实际幅度。
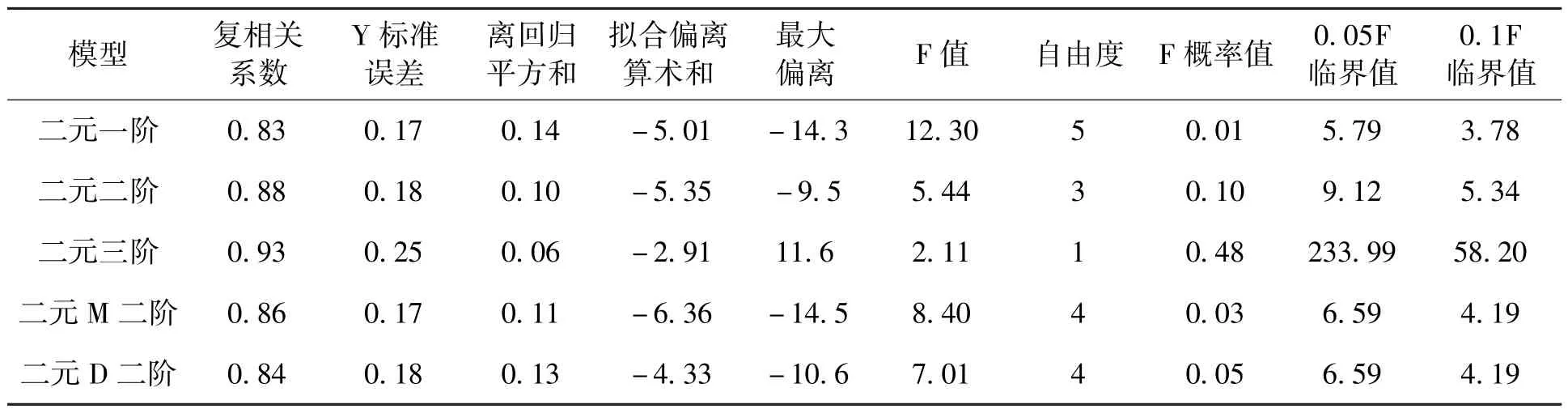
表3 各种回归模型计算结果及F检验Tab.3 Calculation results of all kinds of regression model and F test
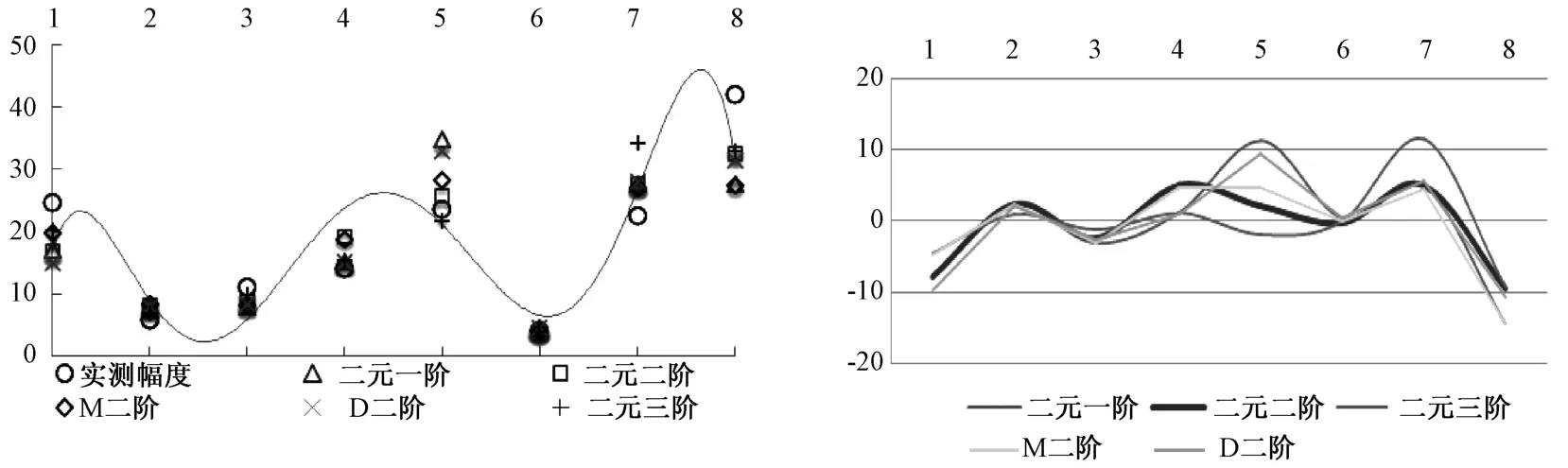
图6 震级、震中距二元不同项式回归结果(左:回归值与实测值右:残差曲线)Fig.6 Two variable regression results of magnitude and epicentral distance(left: return value with the measured values right: residual curve)
二元一阶模型计算得到的关系式为:
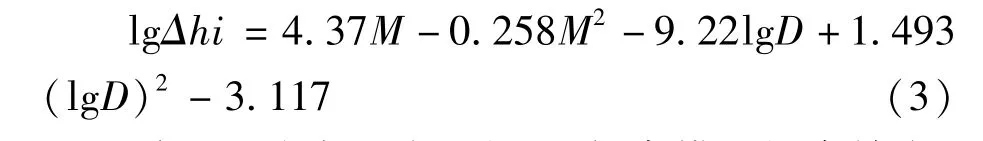
采用2阶多项式回归,可提高模型拟合精度,但由于样本数有限,本文所做尝试尚需进一步深入研究和应用检验。
5 结论与讨论
通过对南昌井水位同震阶跃现象的系统梳理,得到以下认识:
(1)南昌井水位对7.5级以上强震具有较好的同震响应能力,且不受震中方位影响,阶跃方向均为下降。
(2)同震响应表现出明显的距离性,在统计样本范围内,响应距离总体上随震级增加,但在各震级档中均存在距离上限,8级以上可达4000km,未记录到大于1500km的MS7~7.4级地震的同震响应;
(3)水位阶跃对短期内连续发生的强震响应能力下降,存在“钝化”现象;
(4)同震响应幅度与震级、震中距满足以下关系式:
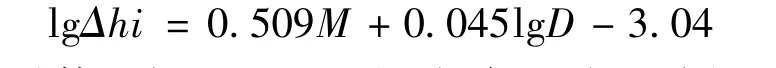
幅度总体上与震级呈正相关,但震中距线性关系不明显;
(5)通过改变模型,对水位振幅与震级、震中距的关系模型进行了优化,得到关系式:
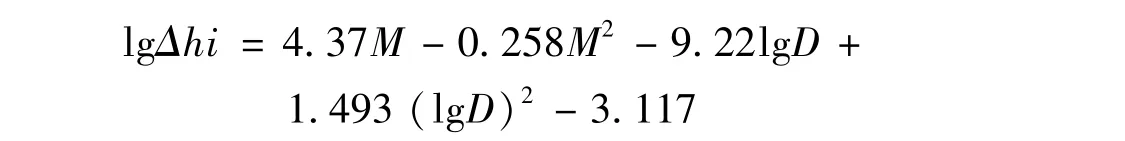
从本例结果看,拟合精度和预测效果优于一阶模型,但二阶回归元的引入尚未给出明确的理论依据。同时,此优化模式是仅属南昌井个别现象抑或具备推广价值,尚需经进一步应用研究。水位乃至流体各测项对地震的同震响应是种共性现象,但每个井孔又各有差异性,如何自差异中提炼出共性,继而指导个性化的深入研究,是值得认真思索的问题。
[1] 简春林.中国大陆地震地下流体异常特征研究[J].地震,2004,24(1):42 -49
[2] 黄辅琼,迟恭才,俆桂明,等.大陆地下流体对台湾南投7.6 级地震的响应研究[J].地震,2000,20(增刊):119-125
[3] 付虹,刘丽芳,王世芹,等.地方震及近震地下水同震震后效应研究[J].地震,2002,22(4):56 -66
[4] 杨竹转,邓志辉,赵云旭,等.云南思茅大寨井水位同震阶变的初步研究[J].地震学报,2005,27(5):569 -574
[5] Roeloffs E A.Persistent water level changes in a well near Parkfield California。due to local and distant earth quakes[J].J Geophys Res,1998,103(B1):869-889
[6] 周松源,张介辉,徐克定,等.从南昌凹陷构造演化分析赣江断裂带运动学特征[J].地质力学学报,2005,11(3):266 -272
[7] 吴敏,赵爱平.南昌地震台数字水位与模拟水位观测对比研究[J].华南地震, 2002,22(4):70 -73
[8] 杨雪超,赵爱平,操红.南昌台气氡异常核实[J].防灾科技学院学报,2007,9(3):43 -47
[9] 杨雪超,高建华,汤兰荣.九江 -瑞昌5.7级地震序列特征[J].防灾减灾工程学报,2006,26(增刊):50-55
Analysis on Coseismic Response of Nanchang Well Water Levels to Teleseismic
Niu Zaipo,Zha Xiaohui
(Earthquake Agency of Jiangxi Province,Nanchang330039,China)
The coseismic response characteristics of the Nanchang well water level to teleseismic has been analysis by summarizing digital data of 139 earthquakes from 2001 to 2008.The two order regression method has also been used to optimize and analyze the model.The results show that the Nanchang well water level has better response to strong teleseismic and the amplitude of the coseismic response is closely related to earthquake magnitude and epicentral distance.The response distance increases with the increase of magnitude, but there is an upper limit of epicentral distance for each magnitude level.
Nanchang well water level; coseismic response characteristics; quantitative analysis model
P315.723 文献标识码:A 文章编号:1673-8047(2017)03-0037-07
2017-03-09
牛在坡(1982—),男,专科,助理工程师,主要从事前兆监测方面的研究工作。

