多车场动态路径问题的自适应量子蚁群算法
郑丹阳, 毛剑琳, 郭 宁, 曲蔚贤, 王昌征
(昆明理工大学 信息工程与自动化学院,云南 昆明 650500)
多车场动态路径问题的自适应量子蚁群算法
郑丹阳, 毛剑琳, 郭 宁, 曲蔚贤, 王昌征
(昆明理工大学信息工程与自动化学院,云南昆明650500)
针对物流配送过程中存在的多配送中心动态需求车辆调度问题即多车场动态车辆调度问题(MDDVRP),提出了一种自适应量子蚁群算法(SAQACA),用于最小化路径。根据量子的相位编码方式,提出了对蚁群的信息素矩阵进行直接编码,进而实现由量子旋转门更新完成蚂蚁移动;根据搜索点的量子相位特点及目标函数的变化率,提出了一种自适应量子旋转门更新方式,进而提高了算法的全局搜索深度;引入基于两元素搜索策略的局部搜索方法提高了算法的局部优化能力,从而对可行解进行改进。仿真实验与算法比较验证了所提算法的有效性和优越性。
多车场动态车辆调度问题; 量子相位编码; 自适应量子旋转门; 两元素搜索策略; 量子蚁群算法
0 引 言
多车场动态车辆调度问题(multi depot dynamic vehicle routing problem,MDDVRP)是由经典动态车辆调度问题中的单个车场变为多个车场衍生而来。目前,较为成熟的启发式算法主要包括遗传算法[1]、蚁群算法[2]、粒子群算法[3]、模拟退火算法等。
在量子算法和蚁群算法应用方面,文献[4]应用改进蚁群算法对飞机路径进行规划并验证了该算法具有较高的求解精度和较快的收敛速度。文献[5]提出了将量子算法与粒子群算法相结合,并通过比较验证了其有效性。文献[6]将双向蚁群算法与微正则退火算法相结合用于求解旅行商问题,并验证了其优越性。文献[7]将改进蚁群算法应用于边缘检测中,并通过仿真验证了其可行性。
在车辆调度与路径规划方面,文献[8]提出了分散搜索算法并验证了算法的有效性;文献[9]提出了改进粒子群算法求解多车场车辆路径问题并验证了算法在速度和寻优效率的有效性和优越性;文献[10]提出了贪婪算法和遗传算法求解仓储车辆调度问题。文献[11]提出行为控制的智能车辆路径规划方式并通过对比实验取得了满意结果。
本文提出了一种自适应量子蚁群算法求解最小配送成本指标下的MDDVRP。在自适应量子蚁群算法(self-adaptive quantum ant colony algorithm,SAQACA)中,将量子相位编码应用于蚁群编码中。同时,提出了一种新的量子旋转门更新方式。此外,引入局部搜索对可行解进行再优化,增强算法的局部开发能力。仿真实验和对比算法验证了SAQACA的有效性和优越性。
1 问题描述及解决方案
1.1 问题描述及数学模型
多车场动态车辆路径问题可描述为:有N个车场,拥有容量为Q的配送车辆Km,m=1,2,…,N辆,现已知客户i到客户j的距离为dij,需对M个客户进行服务,客户i的货物需求为qi,i=1,2,…,M,且qi 设客户编码为1,2,…,M,车场编码为M+1,M+2,…,M+N,定义变量如式(1)所示 (1) 目标函数 (2) 约束条件 (3) (4) (5) i=m∈{M+1,M+2,…,M+N},k∈{1,2,…,Km} (6) k∈{1,2,…,Km} (7) k∈{1,2,…,Km} (8) 模型中,式(2)为目标函数,为最短路径;式(3)确保车场的车辆足够为客户服务;式(4)、式(5)确保每个客户由一辆车服务一次;式(6)确保每辆车均返回车场;式(7)确保每辆车的装载量不超过其容量;式(8)确保车辆不能从一个车场行驶到另一个车场。 在某时刻,出现t个新用户,此时假设未服务客户数与新客户的总和为r,已派出车辆数为s,每辆车的剩余装载量为Qs,s=1,2,…,S,虚拟配送中心编号为T+1,T+2,…,T+S,原车场编号为T+S+1,T+S+2,…,T+S+N,车场剩余的可用车辆为Rm,m=1,2,…,N辆,即 (9) i=m∈{T+S+1,T+S+2,…,T+S+N} (10) (11) (12) (13) i=m∈{T+1,T+2,…,T+S+N}, k∈{1,2,…,Rm} (14) k∈{1,2,…,Rm} (15) S+N},k∈{1,2,…,Rm} (16) 模型中,式(9)为目标函数;式(10)、式(11)确保所派车辆数不超过车场所拥有的车辆数;式(12)、式(13)确保每个客户仅被服务一次;式(14)确保每辆车均返回车场;式(15)、式(16)确保每辆车均不超过其装载量。 采用择近原则对每个客户进行车场分配,具体流程如图1所示。 图1 MDDVRP分配流程 SAQACA采用量子相位编码方式对信息素矩阵进行编码,达到由量子位直接控制蚂蚁的移动方向和增大算法搜索范围的效果,即对问题规模为m+n,m为需求客户数,n为车场数,则生成[2×(m+n)]×(m+n)的信息素矩阵。 信息素矩阵更新策略的设计直接影响算法的收敛速度和寻优效果。在SAQACA中,信息素矩阵更新策略是将蚂蚁当前位置的适应度值函数与信息素相结合,即 τij(t+1)=(1-ρ)τij(t)+Q/Lk,0<ρ<1 式中ρ为信息素的挥发程度;Q为常系数;Lk为第k只蚂蚁经过路径的总长。 (17) 在SAQACA中,根据搜索点的量子比特和目标函数的变化率设计量子旋转门的更新策略,即 (18) SAQACA主要包括信息素矩阵的量子比特编码、信息素更新、自适应量子旋转门更新、两元素再优化等,使算法的收敛性和寻优性有所提高,SAQACA步骤如图2所示。 为了对SAQACA的性能进行验证,将SAQACA与2种其变形算法进行比较。对一个随机生成的MDDVRP进行求解,车场和用户均分布在100×100的范围内,车辆的最大容量为25,具体如表1~表3所示。每种算法均独立重复运行20次,每次运行的迭代次数为100次。 图2 SAQACA算法流程 SAQACA的关键操作主要包括:使用QACA;使用非确定旋转角的自适应量子旋转门更新策略;使用最优解再优化策略。 为了考察上述操作的有效性,考虑如下变形算法: 1)QACA。 2)自适应量子旋转门调整策略代替标准的量子旋转门的量子蚁群算法(SAQACA_V1)。 3)在SAQACA_V1的基础上加入两元素邻域搜索进行最优解再优化SAQACA。 表1 原始客户 表2 新增客户 表3 配送中心坐标 SAQACA与其变形算法的比较结果如表4所示。 表4 SAQACA与其变形算法比较结果 由表4可知:SAQACA_V1解的质量明显优于QACA,说明在求解MDDVRP时,自适应量子旋转门更新策略优于传统量子旋转门更新机制;SAQACA解优于SAQACA_V1,表明加入有效的局部搜索对可行解进行再优化可再提高最优解的质量。综上,SAQACA中的自适应量子旋转门更新策略有助于提高算法的全局搜索能力,基于两元素局部搜索可加强算法的局部搜索能力,从而使算法在全局搜索和局部搜索之间达到较好的平衡,有效求解MDDVRP。 标准量子遗传算法(QGA),QACA,以及采用非固定旋转角的自适应量子旋转门更新方式,即自适应量子遗传算法(SAQGA)。采用实验设置中的数据, SAQACA与QGA,QACA,SAQGA的比较结果如表5所示。 表5 SAQACA与其他算法比较结果 由表5可知,SAQACA的结果明显优于QGA和QACA,SAQGA2种算法,表明SAQACA求解MDDVRP的优越性和有效性。综上所述,SAQACA是求解MDDVRP的一种优越且有效的算法。 首次提出了一种SAQACA用于求解多车场动态车辆调度问题。在算法改进上,SAQACA将量子相位编码应用于蚁群编码中,使量子比特控制蚂蚁的移动;此外,SAQACA应用一种新的改善蚁群的进化方向的量子旋转门策略更新提高了算法的全局搜索能力;最后,通过引入再优化策略提高了算法的局部搜索能力。通过算法比较验证了SAQACA求解MDDVRP的有效性和优越性。下一步工作将针对调度问题和量子算法进行更深入研究。 [1] Berger J,Salois M,Begin R.A hybrid genetic algorithm for the vehicle routing problem with time windows[C]∥12th Biennial Conference of the Canadian Society for Computational Studies of Intelligence on Advances in Artificial Intelligence,1998:114-127. [2] Wang Gengsheng,Yu Yunxin.An improved ant colony algorithm for VRP problem[C]∥Intelligent Information Technology and Security Informatics,2011:129-133. [3] Zhu Yuhua,Ge Hongyi,Zhen Tong.Hybrid particle swarm algorithm for grain logistics vehicle routing problem[C]∥Intelligent Information Technology Application,2009:364-367. [4] 倪 壮,肖 刚,敬忠良,等.改进蚁群算法的飞机冲突解脱路径规划方法[J].传感器与微系统,2016,35(4):130-133. [5] 陆建山,周鸿波,谢伟东.基于量子粒子群优化的动态标定辨识方法[J].传感器与微系统,2016,35(6):27-30. [6] 周浩理,李太君,肖 沙,等.微正则退火的双向蚁群优化算法[J].传感器与微系统,2016,35(4):127-129,133. [7] 李国宁,李沛齐,王燕芩.基于改进蚁群算法的轨道图像边缘检测方法[J].传感器与微系统,2013,32(6):130-133. [8] 张 军,唐加福,潘震东.求解多车场车辆路径问题的分散搜索算法[J].系统工程,2009,27(6):83-90. [9] 王铁君,邬开俊.多车场车辆路径问题的改进粒子群算法[J].计算机工程与应用,2013,49(2):5-8. [10] 王友钊,彭宇翔,潘芬兰.基于贪心算法和遗传算法的仓储车辆调度算法[J].传感器与微系统,2012,31(10):125-128. [11] 李舜酩,沈 峘,鲍庆勇.未知环境下基于行为控制的智能车辆路径规划研究[J].传感器与微系统,2010,29(4):67-70. Self-adaptivequantumantcolonyalgorithmforsolvingmultidepotdynamicvehicleschedulingproblem ZHENG Dan-yang, MAO Jian-lin, GUO Ning, QU Wei-xian, WANG Chang-zheng (SchoolofInformationEngineeringandAutomation,KunmingUniversityofScienceandTechnology,Kunming650500,China) Aiming at multi depot dynamic vehicle routing problem(MDDVRP)existed in the process of logistics distribution,self-adaptive quantum ant colony algorithm(SAQACA)is proposed to minimize the distribution cost.According to the quantum phase encoding method,directly encoding of pheromone matrix of ant colony is presented to complete the movement of ants.According to quantum phase characteristics of search point and object functions change rate,a mode of adaptive quantum rotation gate is presented,to enhance global search depth,the local search method based on the principle of the two elements is introduced to enhance local optimization ability,so as to improve feasible solution. Simulation experiments and algorithm comparison demonstrate the effectiveness and the superiority of proposed algorithm. multi depot dynamic vehicle routing problem(MDDVRP); quantum phase encoding; adaptive quantum rotation gate; two element search strategy; quantum ant colony algorithm 10.13873/J.1000—9787(2017)10—0133—04 2016—08—22 TP 301.6 A 1000—9787(2017)10—0133—04 郑丹阳(1992-),女,硕士研究生,研究方向为算法优化,车辆调度。1.2 解决方案

2 SAQACA
2.1 量子相位编码信息素矩阵
2.2 信息素更新规则
2.3 蚂蚁移动规则

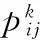
2.4 自适应量子旋转门与相位更新


2.5 SAQACA步骤
3 仿真实验与算法比较
3.1 实验设置




3.2 SAQACA与其变形算法比较

3.3 SAQACA与其他算法比较

4 结束语

