具有零漂容忍度和非线性校正功能的电磁流量计仪表系数计算方法

汪春畅 许 伟 徐科军 吴建平 梁利平

(合肥工业大学电气与自动化工程学院)

具有零漂容忍度和非线性校正功能的电磁流量计仪表系数计算方法

汪春畅 许 伟 徐科军 吴建平 梁利平

(合肥工业大学电气与自动化工程学院)

针对部分国产电磁流量计通过了出厂标定，但再次校验时误差超差的问题，进行了大量实验研究。确定造成小流速点超差的原因为仪表的零点漂移和非线性特性。分析了目前常用的几种计算仪表系数方法存在的问题，提出分段线性拟合仪表系数计算方法。该方法同时兼顾小流量点和大流量点的误差，为仪表的可能零点漂移预留较大的空间，克服仪表的非线性特性，使电磁流量计再次校验或应用时都能满足测量准确度的要求。

电磁流量计 超差 零点漂移 非线性 仪表系数 分段线性拟合

电磁流量计是基于电磁感应原理工作的，较为广泛地应用于工业行业的水流量和浆液流量测量[1～3]。随着工业的发展，对电磁流量计的测量准确度提出了更高的要求。然而，有些电磁流量计在出厂标定时能够达到测量准确度的要求，但是，若再次检验(校验)，此时往往需要重新夹装,或者将一次仪表转90°安装,或者安装到别的管道上(均符合安装要求)，测试结果就达不到测量准确度的要求，主要表现为：在小流量点时测量误差超过指标规定的范围，即所谓的超差。这样就不能保证现场的测量准确度，因为电磁流量计用于现场时肯定要重新夹装。同时也无法满足产品出口的要求，因为国外会对出口的产品进行校验。

国内外学者曾深入研究过电磁流量计在管道90°转角处安装角度对测量误差的影响，分析原因为流场紊乱，并计算出最佳安装角度为45°，还研究了电磁流量计安装未对准对其性能的影响[4,5]。但是，很少研究电磁流量计通过出厂标定，但再次检验超差的问题。这一问题严重影响了电磁流量计的实际测量准确度和国际市场的拓展。为此，笔者进行大量的实验研究，寻找电磁流量计再检验时不满足测量准确度的原因；分析目前常用的几种计算仪表系数方法存在的问题；提出新的仪表系数计算方法，并进行实验验证，以使电磁流量计在有一定的零漂和非线性情况下也能保证其测量准确度。

1 影响测量准确度的因素

通过实验和分析发现，电磁流量计标定时达到测量准确度的要求，而再次检验时小流速点超差，主要是由两个因素引起的：一是电磁流量计的零点漂移，二是仪表的非线性特性。

1.1 零点漂移

零点是指在零流量情况下，电磁流量计输出信号经过滤波和幅值解调后的感应电动势值。零点漂移是指零点偏离固定值而往上或者往下漂动的现象。产生零点漂移的原因有：

a. 变送器中的电子器件，如运放、电容等的温度漂移。电磁流量计安装在测量现场，环境温度会变化；电磁流量计工作时，本身的电子元器件也会发热。若电子元器件本身的温度特性不好，就会产生温度漂移，从而造成流量不变时，输出的电压信号发生变化。

b. 励磁电流不稳定。根据电磁流量计的工作原理，电极输出的感应电动势的稳定性取决于磁场的稳定性，而磁场的稳定性又取决于励磁电流的稳定性。若励磁电流不稳定，就会造成零点漂移。

由于误差计算为测量值与真实值之差与真实值的比值，因此流速越小，零点漂移带来的影响越大。

1.2 仪表非线性特性

通常认为电磁流量计的特性是线性的，即被测流速与测得的电动势幅值之间是线性关系，可以y=ax来表示，其中，a为线性系数。若是线性特性，则不同流速点的仪表系数应该相同，而实验数据表明，不同流速下的仪表系数是有差别的。在两个不同的时间段标定电磁流量计在10个不同的流速点下的线性仪表系数，每个流速点均标定了两次，发现不同流速下的线性仪表系数是不同的，且大流速与小流速的仪表系数相差较大。例如，在流速为5.5m/s时，线性系数为9.216 4；在流速为0.3m/s时，线性系数为9.257 2，相差了0.040 8。若选9.216 4为仪表系数，则测量误差为0.0408/9.2164=0.443%，比较大。

2 计算仪表系数现有的方法

由于仪表材料和制造工艺方面的原因，电磁流量计不可避免地会存在一定的零点漂移和非线性特性。为此，必须研究合适的仪表系数计算方法，以便为电磁流量计的零点漂移留出一定的容错空间，且能够表征其非线性特性。所谓仪表系数是指可通过修改其数值而改变流量计计量性能的参数，它可以由一个或一组参数构成。目前，主要有4种计算仪表系数的方法：去零点法、最小二乘拟合法、基于示值误差拟合法和均值法。笔者以容积法标定DN40mm电磁流量计为例来分析存在的问题。

2.1 去零点法

基于去零点法的仪表系数由一次项系数k和零点z组成，并由标定实验数据计算得到。该方法认为感应出的电动势信号中存在一个固定的幅值，即流速为零时输出的幅值大小。根据这个前提，可在零流量状态下计算出零点。得到零点的具体做法是：先设置k为1、z为0。在流量为零的情况下，用被检表测量一段时间内的累计流量，根据时间和管道口径等信息计算出零点，即为z值。得到一次项系数的具体做法是：在设置完z值后，k为1保持不变，将瞬时流量调节到量程中点，分别使用标准器和被检表同时测量一段时间内的标准累计流量和测量累计流量，计算它们的比值，即为k值。

通过影响测量准确度的因素分析知道，在实际情况下，零点是会发生漂移的，而去零点法只是采用一个很短时间段内的测量结果作为零点，所以，当仪表长时间工作时，小流量点的测量误差会受影响。为此，选择一台精度为0.5%的电磁流量计，由去零点法计算出仪表系数，在间隔数天的时间进行了两次检定实验，检定实验结果如图1所示，其中，第1次检定的时间为t1～t2，测量误差结果为曲线I，第2次检定的时间为t3～t4，测量误差结果为曲线Ⅱ。可见，当零点在正常范围zmin～zmax内变化时，选择的仪表在测量小流量时已经不能满足精度要求。

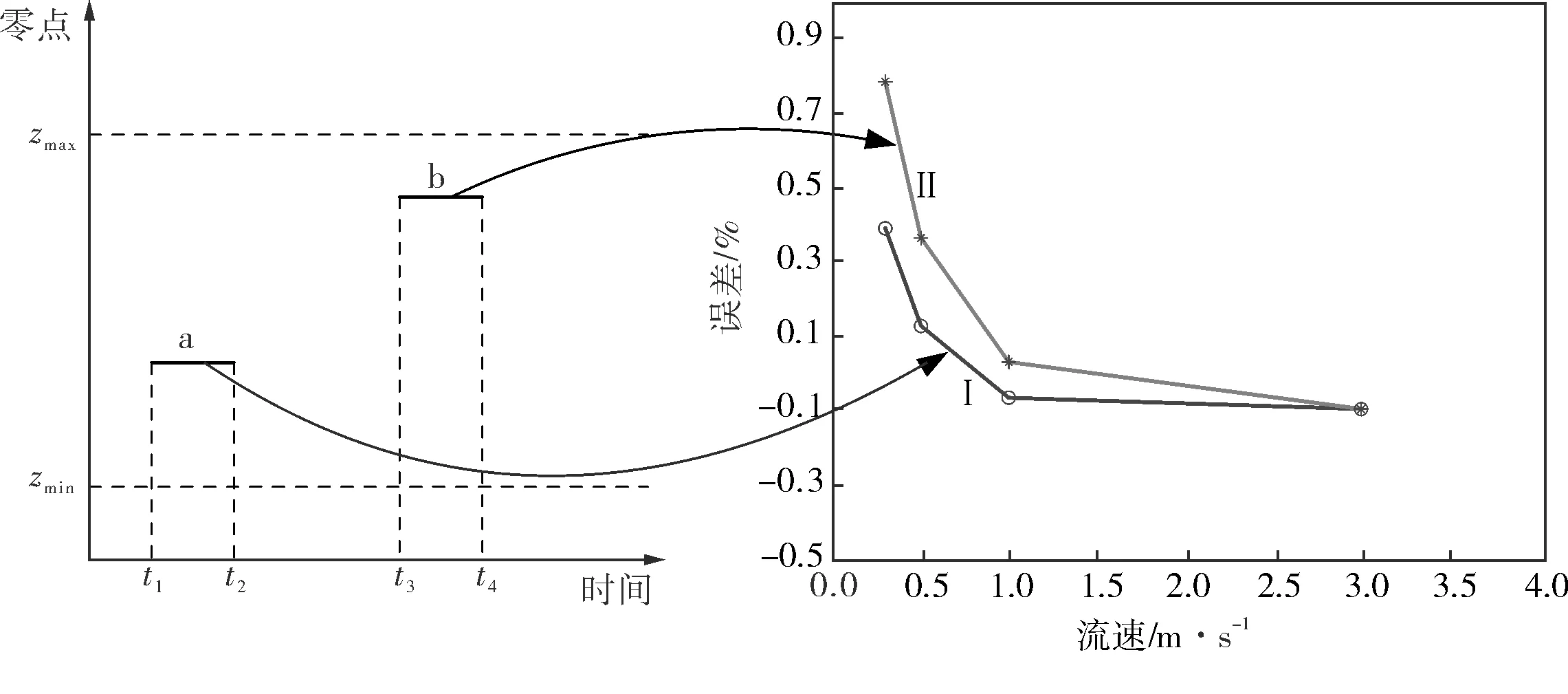
图1 零点漂移下各流速点误差的变化

2.2 最小二乘拟合法

该计算方法是基于绝对误差大体相同的前提下对标定实验数据进行最小二乘拟合，即拟合样本中所有数据的拟合结果与标准值之间的绝对误差大体一致[6,7]。但是，在检定规程中，是采用示值误差来表示流量计的准确度等级。示值误差等于测量流速与标准流速的差除以标准流速。可见，同一准确度等级的电磁流量计，其测量流速越大，允许的绝对误差就越大，而测量流速越小，允许的绝对误差就越小。所以，采用基于绝对误差的最小二乘法计算出仪表特征系数的电磁流量计在测量大流速时，示值误差小；在测量小流速时，示值误差比较大。最小二乘拟合法对当前数据拟合后不能保证小流速点的误差较小，且可能超出测量准确度范围。因此，该方法也没有留出足够的容错空间来减小零点漂移对小流速点精度带来的影响。

2.3 基于示值误差拟合法

该计算方法把各个流速点的示值误差的平方和最小作为数据拟合的目标，给予小流速点更多的关注，使测量流速与标准流速之间的示值误差的平方和最小。该方法先设置电磁流量计的仪表系数中一次项系数和常数项系数分别为k=1和b=0。通过标定得到各个流量下的标准流速、平均感应电动势，再对标准流速、平均感应电动势进行拟合得到仪表系数k和b。测量流速yi与感应电动势xi的关系如下：

yi=kxi+b

基于示值误差拟合法是通过常数项系数b来实现对小流速点补偿的，且对当前数据的补偿效果较好，当仪表长时间工作，零点发生漂移时，小流量点的测量误差可能会受影响。为此，选择一台精度为0.5%的电磁流量计，进行标定实验并由基于示值误差拟合法计算出仪表系数，在间隔数天后进行检定实验，实验结果如图2所示，可见，选择的仪表在检定实验中小流量已经不能满足精度要求。

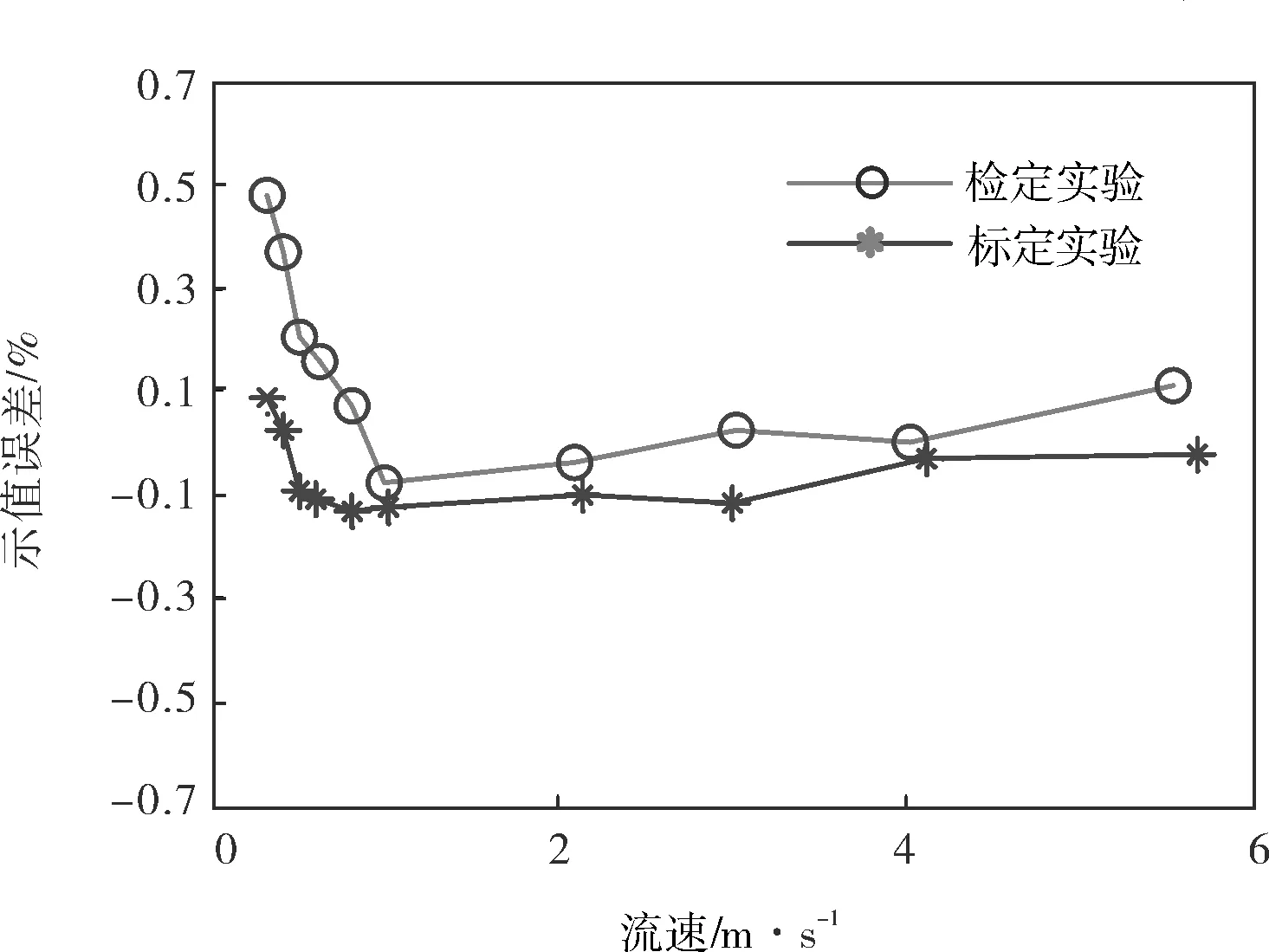
图2 标定实验和检定时各流速点的示值误差

2.4 均值法

该计算方法将若干个流速下的线性系数的均值作为仪表系数，只得到一个参数，即一次项系数k。按照与第3种仪表系数计算方法相同的实验步骤，得到设定的若干个瞬时流量下的线性系数，且仪表系数为各瞬时流量点下的线性系数的平均值。

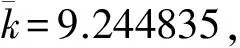
3 新的仪表系数计算方法

为了克服这些仪表系数计算方法的不足，笔者提出一种基于分段线性的电磁流量计仪表系数计算方法。该方法考虑到仪表的零点漂移和非线性问题，直接从每个流量点的线性系数出发，对不同流速点下的线性系数采用分段线性拟合，使小流速段的误差较小(小于0.2%)；同时，使大流速段的误差也较小。由于这种方法兼顾大流速和小流速，为零点漂移预留较大的容错空间，从而保证再次检验时的测量准确度。一般来说，对不同流速点下的线性系数分两段进行拟合，即大流速点和小流速点分别采用不同的仪表线性系数。若分两段不能满足要求，可适当增加分段数。下面以分两段为例来说明该方法的步骤。

新的仪表系数计算方法具体步骤如下：

a. 选择6个流速点，分别为1.0qmin、1.5qmin、2.5qmin、3.0qmin、6.0qmin和10.0qmin，或选择5个流速点，分别为1.0qmin、1.5qmin、3.0qmin、6.0qmin和10.0qmin，其中，qmin为仪表所能测量的流速下限。由于随着流速的减小，线性系数的最大相对变化率在增大，因此，在靠近小流速点的范围内，流速点选得相对密些。

b. 根据选取的流速点，进行标定实验，得出各个流速点的线性系数。

c. 观察仪表线性系数的变化趋势，找出线性系数最靠近仪表线性系数最大值和最小值平均值的流速点，并以此流速点作为分界点，把整个流速范围分成大流速区间和小流速区间。

d. 分别计算大流速区间的仪表系数和小流速区间的仪表系数。对大流速区间的所有流速点的线性系数求平均，作为大流速区间的仪表系数；用同样的方法可得到小流速区间的仪表系数。

针对DN40mm的电磁流量计，采用分段线性仪表系数计算方法计算出仪表系数，进行了两次检定实验，两次检定实验间隔数天，且第2次检定实验前将传感器旋转90°后重新安装。两次检定实验的流速点包括5.0、3.0、1.0、0.5、0.3m/s，每个流量点检定3次，取3次误差的平均值作为每个流量点的误差，两次检定实验的结果见表1、2。可见两次验证实验的示值误差均小于0.3%，重复性误差均小于0.1，达到0.3级精度要求。

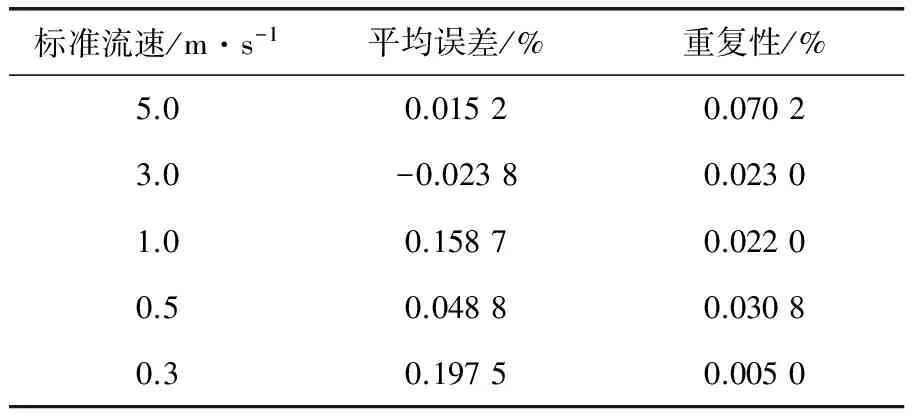
表1 第1次检定实验结果

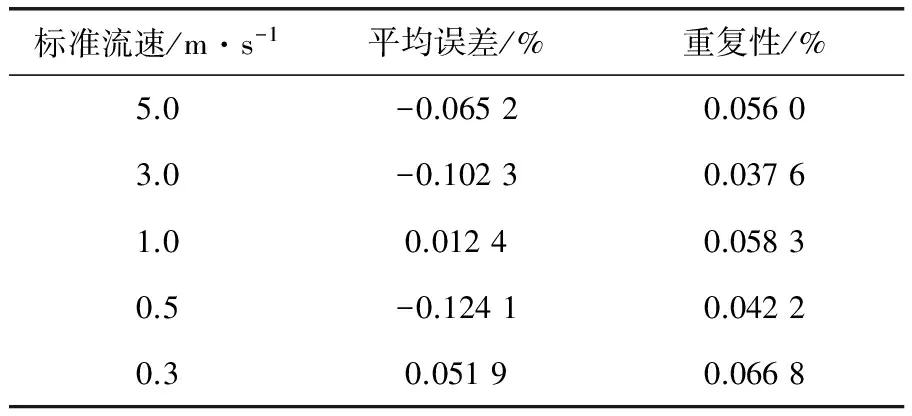
表2 第2次检定实验结果

在某大型流量仪表厂的检定站，采用笔者方法计算出仪表系数，并对DN300mm电磁流量计进行水流量校验。按厂家要求，选取3个流速点进行校验，分别为满量程的10%、60%和100%。这两次验证实验的示值误差均小于0.3%，重复性误差均小于0.1，达到0.3级精度要求。可见，采用笔者方法计算出的仪表系数，对重新夹装的DN40mm和DN300mm电磁流量计进行校验，测量准确度均为0.3级，有效地保证了电磁流量计的测量准确度。

4 结束语

提出的分段线性拟合仪表系数计算方法能兼顾小流速点和大流速点的测量误差，且计算量小，应用方便。针对小流速点线性系数波动较大的问题，可以为小流速点提供更大的容错空间，避免校验时出现测量准确度不达标的问题。当零点漂移在一定范围内时，不用去零点，标定和检定的精度都能满足要求。

[1] 张振, 徐科军, 杨双龙,等.具有快速响应的电磁流量计高低压励磁系统[J].电子测量与仪器学报, 2013, 27(6):562～571.

[2] 张然, 徐科军, 杨双龙,等. 采用梳状带通滤波的电磁流量计信号处理系统[J].电子测量与仪器学报,2012, 26(2):177～183.

[3] Liang L P, Xu K J, Wang X F, et al. Statistical Modeling and Signal Reconstruction Processing Method of EMF for Slurry Flow Measurement[J]. Measurement, 2014, 54(6):1～13.

[4] Lim K W, Chung M K. Numerical Investigation on the Installation Effects of Electromagnetic Flowmeter Downstream of a 90° Elbow-laminar Flow Case[J]. Flow Measurement & Instrumentation, 1999, 10(3):167～174.

[5] Peng Z, Cao Z, Xu L, et al. Influence of Installation Angle of Electromagnetic Flowmeter on Measurement Accuracy[C].IEEE International Symposium on Instrumentation and Control Technology.Piscataway,NJ:IEEE, 2012:195～199.

[6] 王浩，范广涵，廖常俊，等.应用最小二乘法完善质量流量计的工作曲线[J].仪器仪表学报，2004，25(6)：770～772.

[7] 李颖，林洪生.基于相对误差的曲线最小二乘拟合[J].沈阳师范大学学报(自然科学版)，2012，30(3):338～342.

CalculationMethodofElectromagneticFlowmeterCoefficientwithZero-driftToleranceandNonlinearCorrectionFunctions

WANG Chun-chang, XU Wei, XU Ke-jun, WU Jian-ping, LIANG Li-ping
(SchoolofElectricalandAutomationEngineering,HefeiUniversityofTechnology)

Aiming at some domestically-made electromagnetic flowmeters which passing ex-works calibration but troubled by the error which exceeding the specified range in re-examination, numbers of experimental studies were performed to show that, both zero-drift and nonlinear characteristics of the meter can result in this error at a small flow rate. Through analyzing the existing calculation methods for the instrument coefficient, a piecewise linear fitting method was proposed which having the errors at small and large flow rates taken into account to reserve a large space for the zero drift and to overcome the nonlinear characteristics. This makes the electromagnetic flow-meter satisfy accuracy measurement when they are re-examined or applied.

electromagnetic flow-meter, out-of-tolerance, zero drift, nonlinearity, instrument coefficient, piecewise linear fitting

TH814+.93

A

1000-3932(2017)09-0837-05

2017-05-05，

2017-05-21)

汪春畅(1992-)，硕士研究生，从事嵌入式系统及其应用的研究。

联系人徐科军(1956-)，教授，从事传感器技术、自动化仪表和数字信号处理的研究，dsplab@hfut.edu.cn。