氢-水同位素催化交换速率及过程模拟的研究进展

王 然，陈晓军，辛 峰

1.中国工程物理研究院 核物理与化学研究所，四川 绵阳 621900; 2.天津大学 化工学院，天津 300350

氢-水同位素催化交换速率及过程模拟的研究进展

王 然1,2，陈晓军1,*，辛 峰2

1.中国工程物理研究院 核物理与化学研究所，四川 绵阳 621900; 2.天津大学 化工学院，天津 300350

氢-水同位素催化交换在处理ITER聚变堆废水以及核裂变反应堆重水升级方面具有应用前景。该交换过程及核心设备催化交换塔的模型化研究，对工艺和工程优化设计具有十分重要的意义。本文重点介绍了氢-水同位素催化交换过程模拟的研究进展，讨论了同位素催化交换速率的计算方式以及吸收塔模型和滴流床模型在同位素催化交换过程模拟中的应用，探讨了氢-水同位素催化交换过程模拟今后的研究方向。通过各类模型的比较，滴流床模型被认为在催化交换过程模拟中有良好应用前景。氢-水同位素催化交换机理及速率计算方法和催化交换塔模型化等方面有待进一步研究。

同位素分离；氢同位素；催化交换；模拟

聚变反应堆和裂变聚变混合反应堆的运行过程中会产生大量含氚废水，以重水为反射层的反应堆中氚也会在重水中累积[1-3]。从反应堆运行、环境保护、经济效益等角度考虑，通过氢同位素分离进行废水处理是必要的。目前，采用的方法有低温精馏、热扩散、催化交换等[3-4]。

采用氢-水同位素催化交换进行氢同位素分离的工艺相较于传统工艺有相当的优势[5]。氢-水同位素催化交换作为一种有前景的重水升级处理方法受到研究者关注[6-7]。早期开发的贵金属催化剂只在气相中有较好的效果。在此基础上开发的工艺流程和操作都很复杂，且能耗大。疏水催化剂开发成功后，采用氢-水催化交换的工艺流程得到大幅简化。常用的疏水催化剂有Pt/SDB和Pt/C/PTFE[8-9]。采用氢-水催化交换的工艺中，液相催化交换(LPCE)工艺流程简单，分离效果良好。组合电解催化交换(CECE)工艺更在此基础上结合了电解池浓集因子较高的优点[10]。LPCE或CECE工艺结合低温精馏被认为是处理国际热核聚变实验堆(ITER)废水较好的脱氚工艺之一[4, 11]。氢-水催化交换亦可用于重水的升级处理[9]。Alekseev等[12]利用组合电解催化交换工艺脱除重水中的氕和氚，可稳定生产高纯度重水。

采用氢-水同位素催化交换工艺的核心设备为催化交换塔。催化交换塔的设计水平、操作参数以及疏水催化剂性能等对分离效果及建设成本有很大的影响[10, 13]。为了降低设计过程的盲目性，实现装置的模型放大并获得优化的操作参数对催化交换塔的设计和操作至关重要。

目前，所采用的模型大多借鉴操作情况类似的设备所采用的模型。通常借鉴的设备主要为填料吸收塔和滴流床。模型的选择方法以及所采用模型的准确度和适用范围受到广泛关注。为了加深对催化交换过程的认识以及促进催化交换塔设计理论的发展，本文将综述氢-水同位素催化交换过程模拟方面的研究进展，并对未来发展方向进行展望，以期对催化交换塔设计和深入模拟研究有借鉴意义。

1 氢-水同位素催化交换机理和过程速率

催化交换速率计算方式对模型的准确性和适用范围往往起决定性影响。采用疏水催化剂的氢-水同位素催化交换过程中，液相水会影响到催化交换的进行，故催化交换被认为只在疏水催化剂孔道内的气相中进行[14]。所以催化交换过程被分为气液相间传质和气相催化交换[5, 15]。以H2-HDO同位素催化交换体系为例[9]，催化交换过程为：

(1)

该过程可分为两步：

(2)

(3)

其中：式(2)为气液传质，式(3)为气相催化交换，式(3)被认为是速率控制步骤。其中，式(2)可采用传统的传质理论进行速率计算。对于气相催化交换步骤，大多研究者采用化学动力学或基于同位素原子守恒计算过程速率。

1.1通过化学反应动力学计算气相交换速率

化学动力学结合传质在处理气液固三相均存在的反应体系方面有较为完善的理论。利用化学动力学研究催化交换过程的速率起步很早。1972年，Rolston等[16]对催化交换过程中的(2)步进行了动力学的研究，其所用催化剂为Pt/Al2O3，并用L-H机理模型解释了速率变化规律，说明了气相催化交换的速率用该方法进行描述是可行的。对于采用Pt负载催化剂的同位素催化交换过程，L-H机理目前仍是气相催化交换主要采用的机理模型[9, 16-18]。对于H2-HDO体系，该机理模型将过程分为以下步骤[17]，并据此导出反应动力学方程。其中a和b为催化剂表面不同的活性位：

(4)

(5)

(6)

(7)

(8)

Kumar等[9]采用L-H机理，对于H2-HDO气相催化交换所推得的气相反应速率方程为：

(9)

其中：p表示各组分分压，Kv为气相催化交换过程平衡常数，ks为反应速率常数，KH2O和KH2分别为水蒸气和氢气的吸附平衡常数。

Kumar等[9]将氢气通过含氘水池进行润湿后，通过Pt/C/PTFE疏水催化剂床层，检测出口HD浓度以研究催化交换速率。根据实验结果，结合了催化剂孔道内扩散，对L-H机理模型推得的动力学方程进行参数拟合。Kumar等[9]根据其实验体系中的D浓度很低，计算得(9)式的拟一级反应速率方程形式。有效因子的计算采用等效平板模型。由此得到的有效因子计算式为：

(10)

(11)

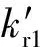
从研究结果来看，用化学动力学计算催化交换速率是可行的[19-20]。选择合适的动力学理论可准确地计算催化交换速率且不会使参数拟合过于复杂。化学动力学理论较为完备，因此该方法结合滴流床的模型对催化交换塔进行模拟可以达到较好的效果。

1.2基于同位素原子守恒计算气相交换速率

采用化学动力学的手段进行催化交换速率计算需要获取或计算得含有同位素的分子浓度。氢同位素丰度往往比含有同位素的分子浓度更易获得。例如，氢气中的氚丰度可通过其放射性直接测得，而HT和T2分子浓度通常需要通过氘丰度计算得到。因此直接采用物质中同位素丰度基于同位素原子守恒计算催化交换速率可能使速率计算的数据处理更加简单。Fedorchenko等[14]将气相催化交换过程总结为：

(12)

其中Ⅰ为H、D或T，此过程中达到平衡时，同位素丰度平衡常数为：

(13)

(14)

其中：Yi和Zi分别为氢气和水蒸气中的氢同位素丰度；k为反应速率常数，其数值受到操作压力、水蒸气分压和温度等因素的影响。Fedorchenko等[14]计算得(14)式的拟一级反应速率方程形式，并利用传质方程的形式处理了催化剂内的孔道扩散。最终得到的有效因子(ε)形式为：

(15)

其中：KY为拟一级反应速率方程的速率常数，Kt为催化剂表面到内部的传质系数。Fedorchenko等[14]通过计算软件对气相催化交换速率和传质参数进行了计算，并计算了温度等因素对速率的影响。

基于同位素原子守恒计算气相催化交换速率比通过化学动力学计算的数据处理相对简单，但是在催化剂中扩散以及流动主体与催化剂间传质方面缺少较完备的理论，将其用于可进行设备设计的模型还需要更深入的研究。

2 催化交换塔的模拟

氢-水同位素催化交换过程通常在催化交换塔中进行。催化交换塔内固定填装疏水催化剂以进行催化交换过程。为了促进气液传质的效果也会同时填装大量亲水填料。催化交换塔通常逆流操作。与催化交换塔比较相近而又有较完善的模拟理论的设备主要有填料吸收塔和滴流床。目前，催化交换塔模拟采用的填料吸收塔模型主要有平衡级模型、沟流级模型和传质模型。滴流床的模型被采用的主要有平推流模型、轴向分散模型、带死区的轴向分散模型等。

2.1填料吸收塔模型

填料吸收塔是常见的分离设备。填料吸收塔与催化交换塔均为固定床层且逆流操作。因此，很多研究人员将填料吸收塔模拟所用的模型用于催化交换塔。被采用的模型主要将全塔视为若干个塔板进行物料衡算；或者采用传质方程进行物料衡算。前者主要有平衡级模型和沟流级模型；后者主要有传质模型。

1) 塔板模型

塔板模型将催化交换塔视为若干塔板，基于同位素丰度平衡理论进行物料衡算。计算塔高时，除了理论板数还需进行等板高度的计算。目前，该方面采用的模型主要有平衡级模型和沟流级模型。

(1) 平衡级模型

平衡级模型计算多用于亲水填料和疏水催化剂分层填装的催化交换塔。平衡级模型将催化交换塔视为若干个平衡级。一个平衡级分别包括一个洗涤床层和催化床层部分。全塔物料分为氢气、水蒸气和水三股物料。假设在洗涤床层上水蒸气和水接触至氢同位素丰度达到平衡；在催化床层上，氢气和水蒸气接触至氢同位素丰度达到平衡[21]，如图1。其中，L、V和G分别为液相水、水蒸气和氢气流量；xi、yi和zi分别为进入第i个平衡级的液态水、水蒸气和氢气中的氢同位素丰度。全塔的液相水、水蒸气、氢气流量不变。

图1 平衡级模型示意图Fig.1 Illustration of equilibrium stage model

基于以上假设对全塔进行物料衡算[21]：

(16)

(17)

Ye等[21]利用平衡级对分层填装Pt/C/PTFE疏水催化剂和θ环的催化交换塔进行了模拟，塔顶氢气中D浓度的模拟值和计算值随温度变化的趋势一致，计算得塔顶HD浓度误差在20%以内。Ye等[21]将实验值和模拟值的误差归结为未完全冷凝的水蒸气对测量的干扰以及对于每一个床层并不可能使物料中同位素丰度达到完全平衡。

Kim等[22]采用平衡级模型对催化交换塔进行了模拟。Kim等[22]模拟了操作温度和进料比等操作条件对分离过程的影响，并认为应该基于LPCE结合低温精馏的全过程对这些参数进行优化。

平衡级模型处理分层填装疏水催化剂和亲水填料的催化交换塔模拟可以达到较高的精度[21]。单个床层有相当高度时，每个床层上达到同位素丰度平衡的假设才可适用。将平衡级模型应用于催化剂和填料混装情况下的催化交换塔模拟有待进一步研究。对于分层填装时的单床层适宜高度以及混装时的等板高度确定目前也无普遍的计算方法。

(2) 沟流级模型

沟流级模型是在平衡级模型的基础上进行改进的模型。全塔物料依然分为氢气、水蒸气和水三股，并假设其流量全塔不变。在每个平衡级上，氢气和水蒸气的一部分经过接触达到同位素丰度平衡；水蒸气和水的一部分经过接触达到同位素平衡。每股物流都未接触的部分直接流过平衡级[23]。以模型中的液相为例，模型中的液相简化示意图示于图2。其中，L为液相水流量；xj为进入第j个沟流级的液态水中的氢同位素丰度；xe表示接触至平衡时液相水中的氢同位素丰度；φL表示第一次沟流的部分所占分数；ω表示第二次沟流的部分所占分数；φVL表示第三次沟流的部分所占分数。基于以上假设，对全塔进行物料衡算[23]。该模型可用于疏水催化剂和亲水填料混装的催化交换塔的模拟。

图2 沟流级模型液相简化示意图Fig.2 Simplified illustration of liquid phase in channeling stage model

Sugiyama等[23]采用沟流级模型对用以脱除ITER产生的含氚废气的催化交换塔进行了模拟。催化交换塔采用θ环和疏水催化剂混装。模型中部分参数借鉴自用以模拟低温精馏的沟流级模型[24]，模型中相互接触部分的物料衡算式为：

L(1-φL)xj-1+V(1-φV)yj+1=

L(1-φL)xe+V(1-φV)ye1

(18)

V(1-φV)yj+1+G(1-φG)zj+1=

V(1-φV)ye2+G(1-φG)ze

(19)

其中：L、V和G分别为液相水、水蒸气和氢气流量；xj、yj和zj分别为进入第j个沟流级的液态水、水蒸气和氢气中的氢同位素丰度。Sugiyama等[23]通过实验数据对剩余未定参数进行了拟合，并将计算的分离效果与实验值相比较。分离因子计算式为：

α=Cextracted water/Cextracted hydrogen gas

(20)

其中：α为分离因子，C为同位素丰度，下标extracted water和extracted hydrogen gas分别表示催化交换过程进行后的水和氢气。计算得分离效果随工艺及操作条件的变化趋势与实验值一致，分离因子的误差控制在50%以内。Sugiyama等[25]进而采用沟流级模型对CECE中的混装催化交换塔进行模拟。催化交换塔进入稳态操作后的模拟得塔顶HTO浓度与实验值误差在10%以内。Sugiyama等[25]考察了氢气流量对过程的影响，并按(20)式计算分离因子，得到的分离因子实验值和计算值误差在10%以内。

沟流级模型在一定的操作范围内可达到相当的精度[25]。相对于平衡级模型，沟流级模型目前有更大的适用范围，可用于催化剂和填料混装的情况下。但如果使用其对催化交换塔进行设计还需要确定等板高度。催化交换过程与吸收和精馏在过程机理上存在较大的差别，沟流级与平衡级之间也存在一定差异。等板高度的确定方法仍有待研究。

综上，塔板模型的方程大多比较简单,在一定的条件下能达到较高的精确度。塔板模型中，沟流级模型可使用与催化剂与填料混装的情况，但是所需确定的参数也较平衡级模型相应增加。在采用塔板模型时，等板高度等参数的确定目前缺乏较普遍的计算方法。因此将塔板模型应用于催化交换塔设计仍有待进一步研究。

2) 传质模型

传质模型与理论板模型均广泛用于填料吸收塔的理论计算。传质模型通过传质方程对催化交换塔全塔进行物料衡算。

(1) 单步传质模型

单步传质模型将气相催化交换和气液传质视为一步进行处理。催化交换塔进行物料衡算得[26]：

(21)

其中：G为气相流率；L为液相流率；a为单位体积床层所提供的有效传质表面积；m为同位素气液平衡常数；y和x分别为氢气和液相含有同位素的分子浓度或同位素丰度；l为床高。很多研究人员在模拟中将Ka视为整体计算[26-29]。

床层内氢同位素丰度变化较大时，同位素的气液平衡常数也会有较大变化。Busigin等[26]将催化交换塔分为若干个有限元，使得每个有限元内气液平衡常数可以视为不变。在此基础上，Busigin等[26]对每个有限元采用传质模型进行处理。Busigin等[26]在Ka为38.89 mol/(m3·s)的情况下对催化交换塔进行了模拟，模拟了不同气相进料D浓度对过程的影响，并得到了全塔同位素丰度分布。

夏修龙等[27]对CECE工艺全流程进行了模拟。其中催化交换塔采用了传质模型。其考察了催化交换塔参数和电解池参数对全流程分离效果的影响，所用Ka为3.0～4.0 mol/(m3·s)。

很多研究者通过计算得到传质系数评价体系的催化交换效果。Singh等[28]将制备的Pt/C/PTFE催化剂与θ环混装于催化交换塔内，通过传质模型计算传质系数，并以此作为催化剂评价的依据。Paek等[29]通过计算得到传质系数，对制备得的Pt/SDBC催化剂活性进行了评价，所得Ka值为0.00～0.02 mol/(g·s)。

单步传质模型计算简单，采用其可较好地反映全过程速率。模型考虑因素较少，且不能反映水蒸气对过程的影响。Sagert等[17]研究表明，水蒸气对催化交换过程速率也会有所影响。全过程Ka值的计算方式也有待进一步研究。

(2) 两步传质模型

为了在模拟中反映水蒸气对过程的影响，部分研究人员将催化交换过程中的气相反应和气液传质两步分别用传质模型进行处理。Shimizu等[30]采用两步传质模型对不同疏水催化剂填装的催化交换塔进行了模拟，其物料衡算式为:

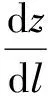
(22)

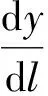
(23)

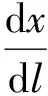
(24)

其中：L、V和G分别为液相水、水蒸气和氢气流量；x、y和z分别为液态水、水蒸气和氢气中的氢同位素丰度或含有同位素的分子浓度；Kg和Kl分别为气相催化交换和气液传质的传质系数；mg和ml为气相催化交换和气液传质的平衡常数；l为床高。Shimizu等[30]分析了Kga、Kla、床层高度等因素对催化交换过程总速率的影响，所假设的Kga和Kla值为49～250 kmol/(m3·h)。

Cristescu等[31]对分层填装的LPCE工艺中的分层填装疏水催化剂和亲水填料的催化交换塔进行了模拟，所用模型为二步传质模型。Cristescu等[31]结合完成不同分离任务的催化交换塔实验数据，对理论板当量高度和传质系数进行了计算，并以此对分离效果进行评价，所测量得到的Kga和Kla值为37～350 kmol/(m3·h)。

夏修龙[32]在对CECE的全工艺流程进行模拟时，采用二步传质模型对CECE工艺中的催化交换塔进行了模拟，并分析了全过程传质系数对分离效果的影响。夏修龙[32]所用的全过程Ka值为3.0～4.0 mol/(m3·s)。

两步传质模型相对于单步传质模型考虑了水蒸气对过程的影响。利用其可分析气相催化交换和气液传质对全过程速率的影响[30]。模型中Kga和Kla值的确定方式仍有待进一步研究。

综上，传质模型在催化交换塔的模拟中被大量采用。该类模型能较简单地获得全塔氢同位素丰度分布，并可以对催化交换塔内催化交换过程速率进行评价[26-32]。模型中所需的参数也少于沟流级模型。传质系数的确定直接影响模型模拟的准确性。不同研究人员模拟中采用或通过实验计算得出的催化交换过程传质系数差别较大，且缺乏通适的计算方式。目前常用的传质系数计算方法并不适用于全过程Ka值和气相催化交换Kga值计算。传质系数的确定方式以及将传质模型用于装置的设计方面仍有待研究。

采用填料吸收塔的模型对催化交换塔进行模拟受到了广泛关注。此类模型大多计算简单。采用的模型中，平衡级模型的计算值与实验值在一定条件下误差较小。沟流级模型较平衡级模型所需确定的参数增加，目前已被使用于填料与催化剂混装的情况。传质模型相对塔板模型能更直观地反映催化交换过程速率。虽然气液传质有大量的研究，但是催化交换过程的机理与单纯的气液传质有很大的不同。单纯的气液传质中并无气固相反应发生。模型中的关键参数的确定无法用常用的手段计算，例如传质模型中的传质系数和沟流级模型以及平衡级模型中的等板高度。此类模型的参数确定方式还需要进一步深入研究。

2.2滴流床模型

滴流床为固定催化剂床层内气液两相流动的反应器，主要用于催化加氢等[33]。滴流床在质量传递和反应机理等方面与催化交换塔更为近似。目前，催化交换塔主要采用的滴流床模型主要有平推流模型、轴向分散模型和带死区的轴向分散模型。

1) 平推流模型

平推流模型是反应工程中的一种理想模型。该模型认为物料在反应器中径向上完全混合，而轴向物料无返混。轴向上物料浓度的变化由物料衡算得到。若采用化学动力学计算催化交换速率，以处理H2-HDO体系的催化交换塔的气相中HD组分为例，其物料衡算式[9]为：

(25)

其中：G为气相摩尔流率；yHD为气相中HD组分摩尔分数；l为床高；rHD为HD的催化交换速率，由前文提到的方法计算。

Ovcharov等[34]对进行重水升级处理的催化交换塔内气相和液相均采用平推流模型进行模拟。催化交换速率基于同位素原子守恒进行计算。Ovcharov等[34]在计算催化交换速率时，采用了不同的速率模型，并与实验值进行比较。实验在分层填装疏水催化剂和亲水填料的催化交换塔内进行。最终Ovcharov等[34]采用拟均相催化交换速率模型时误差最小，塔底产品和废气中的D丰度计算值与实验值误差在1%以内。

Kumar等[9]对用以处理H2-HDO体系的催化交换塔的气液两相均采用平推流模型进行了模拟。塔内混装拉西环和Pt/C/PTFE疏水催化剂。催化交换速率采用化学动力学的方式进行计算并考虑了催化剂内扩散和外扩散的影响，速率参数由气相实验拟合得到。气液传质系数由经过修正的恩田关联式获得。计算所得的塔顶HD浓度和实验值误差控制在20%以内。

采用平推流模型对过程模拟的计算量较小，因此平推流模型在催化交换过程中经常被采用进行动力学研究。催化交换塔中，气相流率相对较大，持液量较小，使得气相返混程度较小，因而用平推流模型对气相进行处理是可行的[9]，且不会使计算过于复杂。但是液相在此情况下的返混较大，因而用平推流进行处理可能误差较大。

2) 轴向分散模型

轴向分散模型是反应工程中较常采用的模型。该模型在平推流的基础上考虑了轴向上的返混。在催化交换塔的模拟中，轴向分散模型的边界条件通常采用闭式边界条件。

Kumar等[9]采用轴向分散模型对催化交换塔中的液相进行处理。塔内混装拉西环和Pt/C/PTFE疏水催化剂。液相的无因次物料衡算式为：

(26)

其中：Pe为Peclet数，由实验获得数据；Ψ为无因次浓度；λ为无因次床高；φL为无因次传质系数，由修正的恩田关联式计算得到。模拟中气相用平推流处理。Kumar等[9]采用此方式进行模拟并将计算的塔顶氢气中HD浓度与实验值相比较，误差在20%以内。Kumar等[9]将该模拟得到的结果与气液两相均采用平推流处理的模拟结果进行了比较，并对催化交换塔的操作条件和工艺条件进行了优化分析。

轴向分散模型将返混对过程的影响进行了简单处理。对于液相流率低、持液量很小的催化交换塔，液相返混对过程的影响比较显著。液相采用轴向分散模型较平推流模型有更高的准确性。轴向分散模型应用广泛，且模型中参数的确定方面有大量的研究[35-36]。采用轴向分散模型对催化交换塔进行模拟是可行的。

3) 带死区的轴向分散模型

在对滴流床的模拟研究中发现，滴流床的实验停留时间分布曲线与通过轴向分散模型计算得到的曲线往往有一定差异[36]。在催化交换塔中，也存在此问题。采用带死区的轴向分散模型拟合得到的停留时间分布曲线相比采用轴向分散模型拟合得到的停留时间分布曲线更接近实验结果[37]。带死区的轴向分散模型将设备分为流动区和死区，其中流动区采用轴向分散模型处理，死区认为不参与流动，只与流动区进行传质[38]。对于无反应体系，其物料衡算式为：

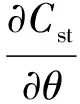
(27)

(28)

其中：C为浓度，下标st和dyn分别表示死区和流动区；NTU为传质单元数；φ为流动区的体积分数；Pe为Peclet数；l为床高；θ为时间。

Kumar等[37]采用带死区的轴向分散模型对分别填装疏水催化剂和填装亲水填料的催化交换塔进行了停留时间分布拟合。得到的拟合曲线与实验结果符合程度很高，均方根误差通常小于10-6。

从停留时间分布曲线拟合情况来看，采用该模型对催化交换塔进行模拟可能会比轴向分散模型有更高的准确度，但是采用该模型进行模拟也会使计算量增大。采用该模型对全塔分离效果的模拟准确度的提高程度有待进一步研究。

综上，滴流床模型在催化交换塔模拟时能较好地反映塔工艺参数和操作条件对分离效果的影响。滴流床模型中常用的模型中参数的确定方式大多也可适用，因此目前在装置设计方面较填料吸收塔模型有更好的应用前景。滴流床模拟的理论完善，有较多模型可以选用。目前采用的模型中，平推流模型计算简单，但未考虑返混等因素对过程的影响。轴向分散模型对返混的影响进行了简单处理。带死区的轴向分散模型在停留时间分布拟合上的误差小于轴向分散模型，因此能更加准确地描述返混。模型中考虑因素的增加，也会使计算量增大而造成求解难度增大,而模型的精度可能不会因此而有较显著提高。如何选择合适的模型仍需进一步研究。

3 分析和展望

研究人员对催化交换过程的模拟方面进行了大量的研究，取得了相当的进展。但仍有以下方面有待深入研究。

(1) 合适的催化交换速率方程

由于过程中相间传质对过程速率有一定影响，而通过同位素丰度直接计算反应速率在处理相间传质方面的理论并不完善，因此用该方法计算操作条件变化较大时的过程速率有待进一步研究。通过化学动力学计算催化交换速率在结合传质方面有较完善的理论，但是目前所采用的动力学形式比较复杂，因此在进行参数拟合时会增加求解难度。采用过于简单的动力学机理模型又会影响催化交换塔模型的适用范围。如何基于化学动力学理论得到合适的催化交换速率方法仍有待进一步研究。

(2) 进一步借鉴滴流床的模拟手段

目前催化交换塔的模拟所采用的模型和手段主要借鉴填料吸收塔和滴流床。从反应和传质的机理上分析，催化交换塔的工艺条件和操作条件更接近滴流床。目前催化交换塔主要采用的滴流床模型中，平推流模型未考虑返混，而根据轴向分散模型所得到的停留时间分布与实验结果有一定偏差。这些问题都会对模拟的准确性产生影响。若在模型中过多地考虑各种因素的影响又会造成求解困难。选择合适的模型因此十分重要。此外，对催化交换塔进行动态模拟也有待进一步研究。CECE工艺中，催化交换塔与电解池等设备中存在物料循环。另外，CECE和LPCE工艺经常与低温精馏结合脱氚也受到广泛关注[4, 11]。采用动态模拟对开工过程和循环过程控制进行研究是有意义的。因此对催化交换过程选取更合适的模型以及更多地借鉴滴流床模拟所采用的手段有助于加深对催化交换过程的认识以及深化催化交换塔设计理论。

4 结 论

氢-水同位素催化交换是在重水升级处理和ITER废水处理方面有相当优势的方法。采用该方法的工艺分离效果良好且流程简单。催化交换过程的模拟研究对催化交换塔的设计和操作至关重要。本文综述了催化交换过程的模拟研究现状和取得成果，对目前所采用的各种方案进行分析并对研究方向进行了展望。随着研究的进一步深入，催化交换塔在设计和操作优化方面的理论将更加完善，对催化交换过程的认识也会更加深入。

[1] Alekseev I A, Bondarenko S D, Fedorchenko O A, et al. Heavy water detritiation by combined electrolysis catalytic exchange at the experimental industrial plant[J]. Fusion Engin Des, 2003, 69(1-4): 33-37.

[2] Vasyanina T V, Alekseev I A, Bondarenko S D, et al. Heavy water purification from tritium by CECE process[J]. Fusion Engin Des, 2008, 83(10-12): 1451-1454.

[3] 阮皓,李金英,胡石林,等.CECE 水-氢交换工艺[J].核化学与放射化学,2011,33(3)：156-161.

[4] Ionita G, Bucur C, Spiridon I, et al. An assessment on hydrogen isotopes separation by liquid phase catalytic exchange process[J]. J Radioanal Nucl Chem, 2015, 305(1): 117-126.

[5] 罗阳明,孙颖.疏水催化剂的研究与应用进展[J].原子能科学技术,2003,37(1)：36-41.

[6] Schwirian A L, van Brunt V. The removal of tritium from aqueous waste streams by catalyzed isotope exchange[C]∥211th ACS National Meeting, New Orleans, LA, Mar 24-28, 1996. Washington, D C: American Chemical Society, 1996.

[7] Rolston J H. Research on the separation of hydrogen isotopes by catalytic exchange[C]∥William J S L. Synth Appl Isot Labeled Compd, Proc Int Symp Amsterdam, Neth: Elsevier, 1983: 385-390.

[8] Ye L, Luo D, Yang W, et al. Improved catalysts for hydrogen/deuterium exchange reactions[J]. Int J Hydrogen Energy, 2013, 38(31): 13596-13603.

[9] Kumar R, Mohan S, Mahajani S M. Reactive stripping for the catalytic exchange of hydrogen isotopes[J]. Ind Eng Chem Res, 2013, 52(32): 10935-10950.

[10] 罗阳明,王和义,刘俊,等.氢同位素氘从气相到液相的催化交换实验研究[J].原子能科学技术,2005,39(1)：49-52.

[11] Ana R G, Cristescu I, Dörr L, et al. Design and experimental activities in view of water detritiation-isotopic separation systems combination in TRENTA facility[J]. Fusion Engin Des, 2009, 84(2-6): 398-403.

[12] Alekseev I, Bondarenko S, Fedorchenko O, et al. Fifteen years of operation of CECE experimental industrial plant in PNPI[J]. Fusion Sci Technol, 2011, 60(3): 1117-1120.

[13] 古梅,刘俊,罗阳明.氢同位素催化交换过程影响因素研究[J].核技术,2013,36(9)：090202.

[14] Fedorchenko O, Alekseev I, Tchijov A, et al. Modeling of the process of three-isotope (H, D, T) exchange between hydrogen gas and water vapour on Pt-SDBC catalyst over a wide range of deuterium concentration[J]. Fusion Sci Technol, 2005, 48(1): 120-123.

[15] Gherghinescu S. Mathematical models for D2-DTO isotopic exchange process of detritiation systems[C]∥Viorel M, Razvan R, Gheorghe D, et al. Recent advances in mathematics and computers in business, economics, biology and chemistry. Athens, Greece: WSEAS Press, 2010: 250-254.

[16] Rolston J, Goodale J. Isotopic exchange between hydrogen and water vapor over supported metal catalysts: part Ⅰ: kinetics of the exchange[J]. Canadian Journal of Chemistry, 1972, 50(12): 1900-1906.

[17] Sagert N H, Pouteau R M L. The Influence of the substrate on hydrogen-water deuterium exchange over carbon supported platinum[J]. Canadian Journal of Chemistry, 1972, 50(22): 3686-3693.

[18] Kawakami K, Takao Y, Kusunoki K. Kinetics of isotopic exchange reaction between hydrogen and water vapor over platinum supported on a hydrophobic carrier[J]. The Canadian Journal of Chemical Engineering, 1986, 64(3): 432-439.

[19] Carriker J, Fleming P, Wagenknecht P S. Kinetic analysis of isotopic exchange between D2(g) and H2O(l) catalyzed by transition metal complexes[C]∥58th Southeast Regional Meeting of the American Chemical Society, Augusta, GA, Nov 1-4, 2006. Washington, D C: American Chemical Society, 2006.

[20] Schwirian-Spann A L, van Brunt V. Hydrogen isotope exchange via catalyzed phase transfer[C]∥ Levan M D. Fundamentals of adsorption: proceedings of the fifth international conference on fundamentals of adsorption. Boston: Kluwer, 1996: 805-812.

[21] Ye L, Luo D, Tang T, et al. Process simulation for hydrogen/deuterium exchange in a packed column[J]. Int J Hydrogen Energy, 2014, 39(12): 6604-6609.

[22] Kim K, Lee M, Paek S, et al. Operational analysis of a liquid phase catalytic exchange column for a detritiation of heavy water[J]. Sep Purif Technol, 2007, 54(3): 410-414.

[23] Sugiyama T, Tanaka M, Munakata K, et al. Development of an improved LPCE column for the TLK facility with the help of the channeling stage model[J]. Fusion Engin Des, 2008, 83(10-12): 1442-1446.

[24] Sugiyama T, Enokida Y, Yamamoto I. Separative analyses of packed water distillation column with channeling stage model[J]. J Nucl Sci Technol, 2000, 37(3): 273-280.

[25] Sugiyama T, Suzuki E, Tanaka M, et al. Hydrogen-tritium isotope separation by CECE process with a randomly packed LPCE column[J]. Fusion Sci Technol, 2011, 60(4): 1323-1326.

[26] Busigin A. Mass transfer model liquid phase catalytic exchange column simulation applicable to any column composition profile[J]. Fusion Sci Technol, 2015, 67(2): 286-289.

[27] 夏修龙,任兴碧,杨通在,等.联合电解催化交换系统分离氢同位素影响因素研究[J].核技术,2008,31(11)：842-845.

[28] Singh M, Singh R, Singh A, et al. Preparation and characterization of hydrophobic platinum-doped carbon aerogel catalyst for hydrogen isotope separation[J]. Bull Mater Sci, 2014, 37(6): 1485-1488.

[29] Paek S, Chung H, Woo S. Preparation, characterization, and reactivity of Pt/SDBC catalysts for the hydrogen-water isotopic exchange reaction[J]. J Radioanal Nucl Chem, 1999, 242(3): 709-715.

[30] Shimizu M, Kitamoto A, Takashima Y. New proposition on performance evaluation of hydrophobic Pt catalyst packed in trickle bed[J]. J Nucl Sci Technol, 1983, 20(1): 36-47.

[31] Cristescu I, Tamm U, Cristescu I R, et al. Investigation of simultaneous tritium and deuterium transfer in a catalytic isotope exchange column for water detritiation[J]. Fusion Engin Des, 2002, 61(2): 537-542.

[32] 夏修龙.联合电解催化交换系统HD/H2O和HT/H2O体系模拟[J].原子能科学技术,2006,40(9)：37-40.

[33] Ranade V V, Chaudhari R, Gunjal P R. Trickle bed reactors: reactor engineering & applications[M]. Holland: Elsevier, 2011.

[34] Ovcharov A V, Rozenkevich M B, Perevezentsev A N.Simulation of CECE facility for water detritiation[J]. Fusion Sci Technol, 2009, 56(4): 1462-1470.

[35] Iliuta I, Thyrion F C, Bolle L, et al. Comparison of hydrodynamic parameters for countercurrent and cocurrent flow through packed beds[J]. Chem Engin Technol, 1997, 20(3): 171-181.

[36] Safinski T, Adesina A A. Two-phase flow countercurrent operation of a trickle bed reactor: hold-up and mixing behavior over raschig rings fixed bed and structured bale packing[J]. Ind Eng Chem Res, 2012, 51(4): 1647-1662.

[37] Kumar R, Pant H J, Sharma V K, et al. Investigation of hydrodynamic behaviour of a pilot-scale trickle bed reactor packed with hydrophobic and hydrophilic packings using radiotracer technique[J]. J Radioanal Nucl Chem, 2011, 294(1): 71-75.

[38] Stegeman D, van Rooijen F E, Kamperman A A, et al. Residence time distribution in the liquid phase in a cocurrent gas-liquid trickle bed reactor[J]. Ind Eng Chem Res, 1996, 35(2): 378-385.

AdvancesinRateandProcessSimulationofCatalyticIsotopicExchangeBetweenHydrogenandWater

WANG Ran1,2, CHEN Xiao-jun1,*, XIN Feng2

1.Institute of Nuclear Physics and Chemistry, China Academy of Engineering Physics, Mianyang 621900, China; 2.School of Chemical Engineering and Technology, Tianjin University, Tianjin 300350, China

Catalytic isotopic exchange between hydrogen and water is prospective to be applied in waste water treatment for fusion reactor such as ITER and heavy water upgrading for fission reactor. Research in modeling the exchange process and the key facility, catalytic exchange column, is significant for optimization and design in engineering and processing. The advances in simulation of catalytic exchange process are mainly introduced. Methods adopted in determining catalytic isotopic exchange rate and applications of absorption tower model and trickle bed model in simulating catalytic isotopic exchange process are discussed. The further development of the research is also suggested. Trickle bed model is considered to be prospective in simulating catalytic isotopic exchange process compared with other models. Mechanism and rate determination of catalytic isotopic exchange between hydrogen and water as well as modeling of catalytic exchange tower still need to be perfected.

isotopic separation; hydrogen isotopes; catalytic exchange; simulation

O643.14

A

0253-9950(2017)05-0336-09

2016-04-26；

2016-09-19

国家国际科技合作专项资助项目(2015DFR60380)

王 然(1992—)，男，湖北武汉人，硕士研究生，化学工程专业，E-mail: wr73064@163.com

*通信联系人：陈晓军(1971—)，男，重庆人，研究员，从事核燃料循环与材料研究，E-mail: cxj839@163.com

10.7538/hhx.2017.YX.2016043