一种新型多智能体固定目标控制算法①

秦补枝

(南京科技职业学院自动控制系)

一种新型多智能体固定目标控制算法①

秦补枝

(南京科技职业学院自动控制系)

提出一种新型的多智能体固定目标控制算法。某个智能体到达固定目标的附近区域时，在该智能体与目标之间增加反馈控制器，使得智能体与固定目标之间的通信量减少。最后通过仿真证明了该算法的有效性。

多智能体 固定目标 控制算法

随着计算机技术和通信网络的迅速发展，复杂网络的研究已经渗透到很多方面，如疾病的传播、交通运输及电力传输等。研究者从复杂网络理论的角度对它们进行分析研究，将这些问题归纳为一个复杂网络系统，每一个执行环节作为一个节点，并且为智能节点，具有复杂动力学行为，由这些节点组成的网络行为就变得异常复杂。因此，分析和控制这些网络的复杂行为成为研究的热点之一[1～18]。 由于网络的拓扑结构和动力学行为相互影响，使这个问题更加难以解决。特别是通过对网络中的少数节点增加线性误差反馈控制，使得整个网络稳定到一个均匀的平衡点状态，即网络中的每个节点的状态都稳定到单个节点的平衡点上[1～3]。这种控制方法增加了每一时刻节点之间的通信量，不易实现。为了减少智能体与固定目标之间的及时通信量，笔者提出了一种基于事件驱动的固定目标跟踪策略，即当某个智能体的状态与固定目标的状态接近时，对该智能体施加反馈控制，使得智能体与固定目标之间的通信量减少，跟踪速度加快，提高跟踪效率。

1 基于事件驱动的多智能体固定目标跟踪方法

假设一个网络由N个相同的节点组成，构成了连续时间耗散耦合的动态网络，其中第i个节点的状态方程为：

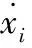
(1)

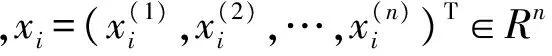
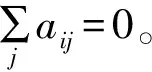
当t→∞时：

x1(t)=x2(t)=…=xN(t)=s(t)

(2)

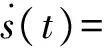
智能体i的事件驱动函数定义为：

αi(t)=‖xi(t)-s‖-β,i=1,2,…,N

(3)

其中β>0 ,‖·‖ 代表欧几里德范数。 笔者设计的控制率为：

ui(t)=-γicμ(xi(t)-s)

(4)

其中μ是跟踪目标与智能体之间的耦合强度；γi由事件驱动函数αi(t) 的符号决定：

(5)

定义矩阵B为：

B={bij}N×N=A-μ·diag[γ1(t),γ2(t),…,γN(t)]

(6)

由文献 [1，2]可知矩阵B是负定，其特征值可以写为0≥λ1(B)≥λ2(B)≥…≥λN(B)。因为事件驱动函数的存在，使得在某些时刻存在所有的智能体都不在跟踪目标的吸引区域内，而不触发事件驱动函数，因此有可能使得式(6)的第2项为0，导致矩阵B的最大特征值为0。

定理1 考虑多智能体(1)，其控制输入(4)在事件驱动函数(5)的作用下，如果矩阵Df(s)+ηIn×n的所有特征值具有负实部，则该多智能体系统能够局部指数稳定到系统的独立状态(2)中的s。其中In×n为n维单位阵，η<0。有：

cλ1(B)≤η

(7)

证明将式(1)在平衡点s附近进行线性化得到：

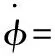
(8)

其中Df(s)∈Rn×n是函数f()在s上的雅可比矩阵，φ=(φ1,φ2,…,φN)T,φi(t)=xi(t)-s。

由式(6)知：

Bφi=λi(B)φi,i=1,2,…,N

(9)

将式(9)代入式(8)得到：

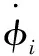
=(Df(s)+cλi(B)I)φi

(10)

i=1,2,…,N

由于0≥λ1(B)≥λ2(B)≥…≥λN(B)，即只需要满足(Df(s)+cλ1(B)I)<0即可使得式(10)中的N个方程式满足指数稳定的条件。由式(7)可知，对于一个非线性函数，其雅可比矩阵可以确定得到，这样选择合适的节点之间的耦合强度c可使得N个方程式满足指数稳定。

在系统的初期，可能会存在所有智能体的状态都不能触发事件驱动函数，即所有的节点状态与所需要达到的固定目标距离比较远，此时对应的λ1(B)=0，因此式 (7)不能写成：

(11)

为了能在系统初始时对选择智能体之间的耦合强度提供一个依据，笔者建议系统初始的耦合强度取为：

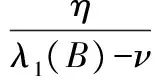
(12)

其中ν>0为一个无穷小的正数。

由于混沌系统存在各态历经性，随着时间的推移，必然有智能体的状态接近固定目标，从而触发事件驱动函数，使得整个系统能够达到跟踪固定目标的目的。

2 仿真结果

复杂动态网络中单个节点的状态为典型的陈系统，其动力学方程为：

(13)

此时，陈系统节点为一个混沌系统(图1)[19]。

图1 混沌的陈系统示意图

令式(13)右端等于零，得到陈系统的一个平衡点(7.9373, 7.9373,21)，将它作为本次仿真的固定目标。

考虑一个经典的由100个节点组成的BA无标度网络模型，它的生成算法可参考文献[20]，初始节点为3个，每增加一个节点增加3条边,单个节点的动力学为陈系统。

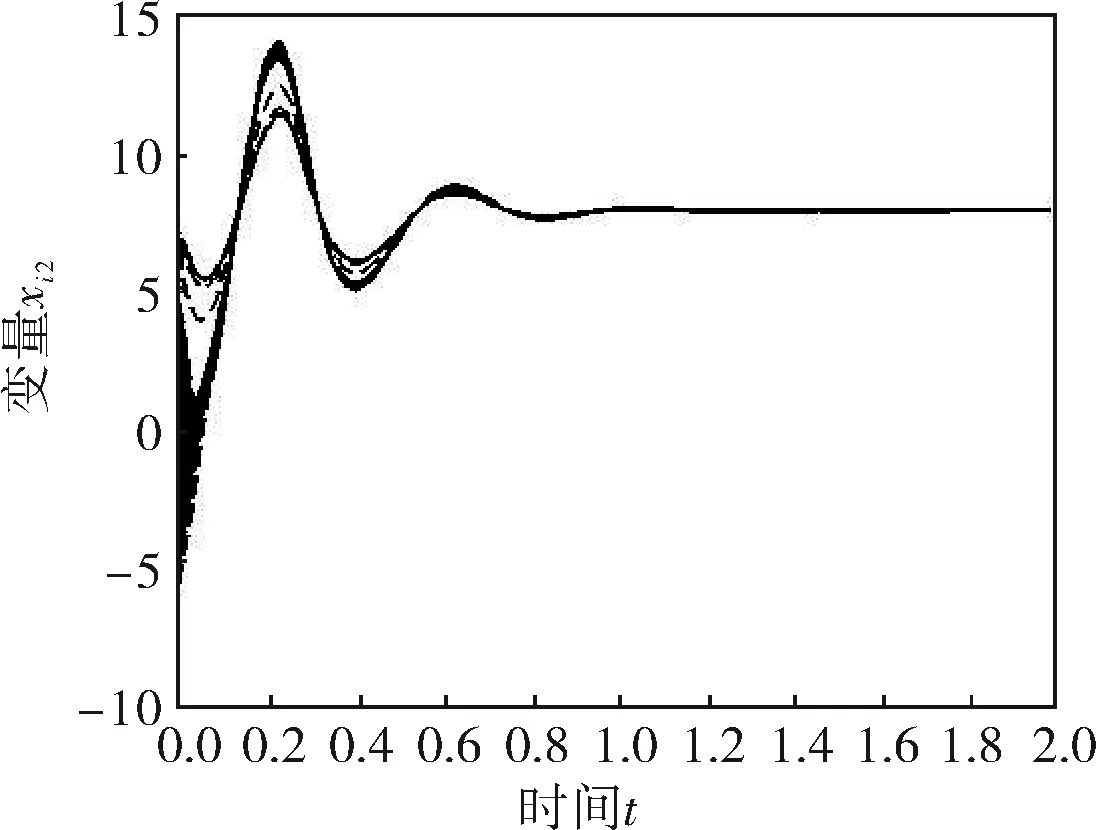
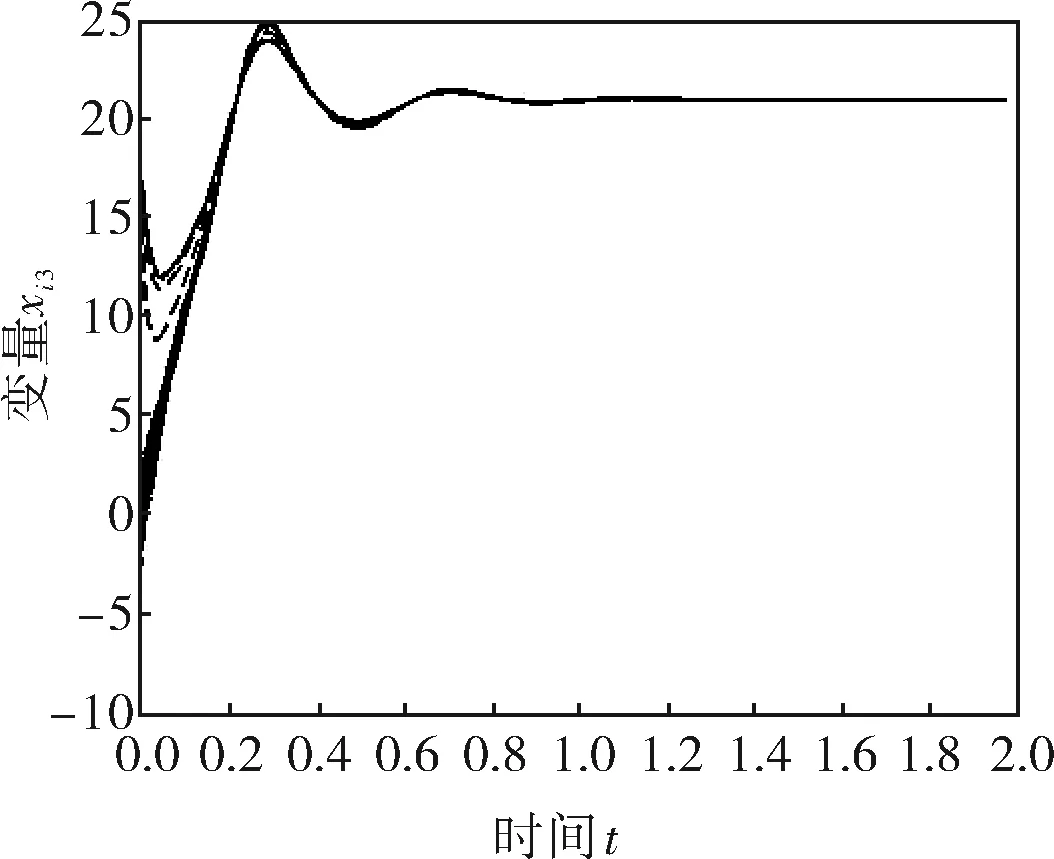
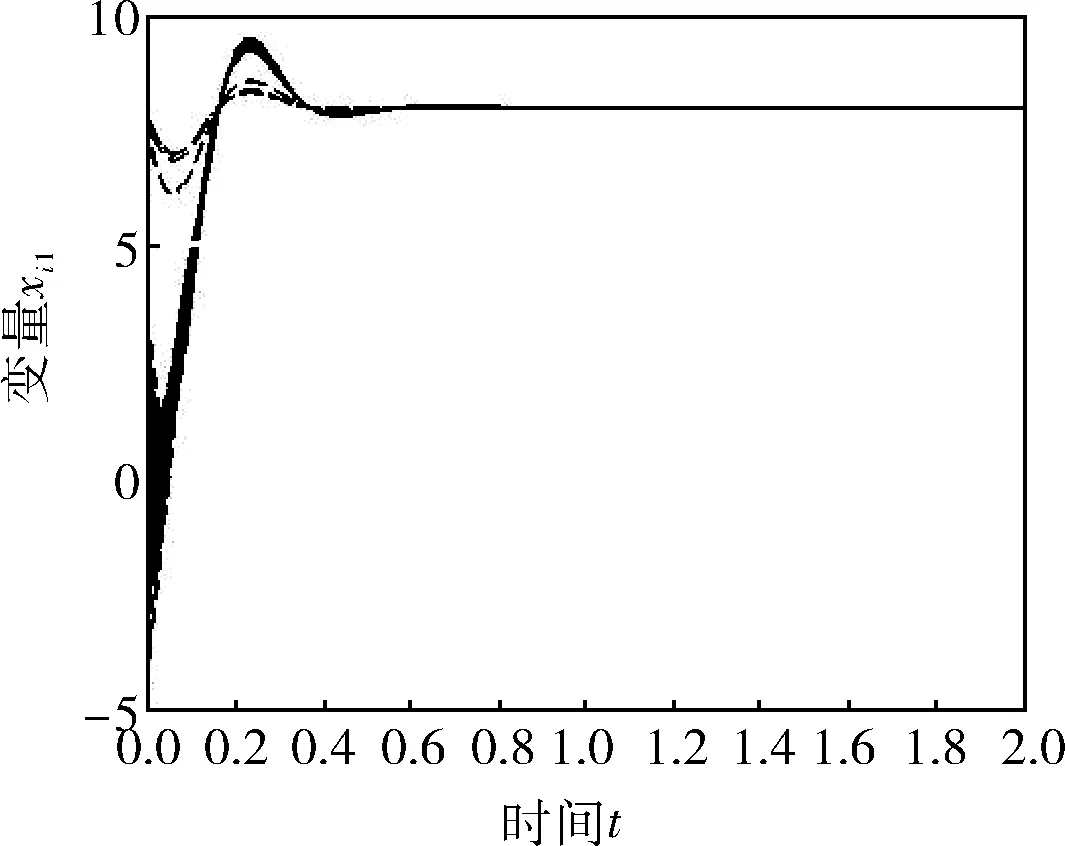
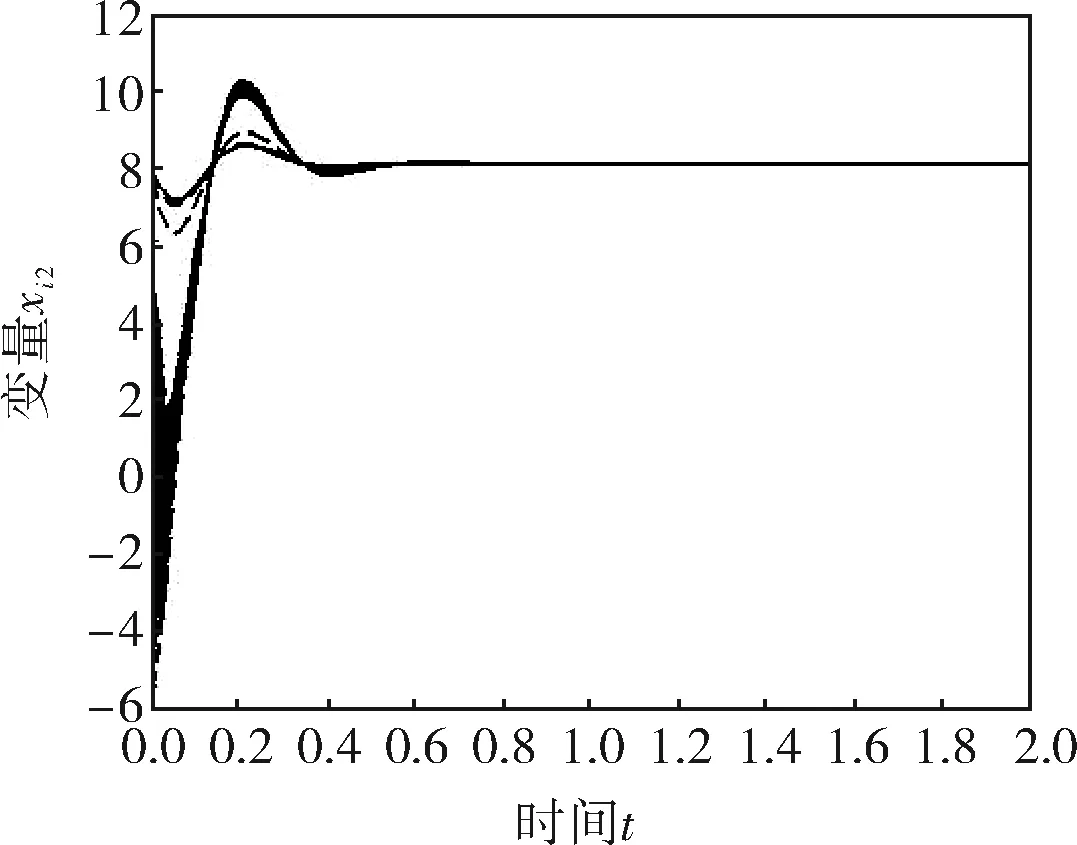
假设每个节点代表一个智能体，它要跟踪的目标为100个智能体的平均状态。在图2、3中，采用的是相同的无标度网络模型，并且节点和跟踪目标之间的耦合强度都设为12，每个智能体的初始状态都随机分布在[-5,5],只有事件驱动函数的参数β发生了变化。

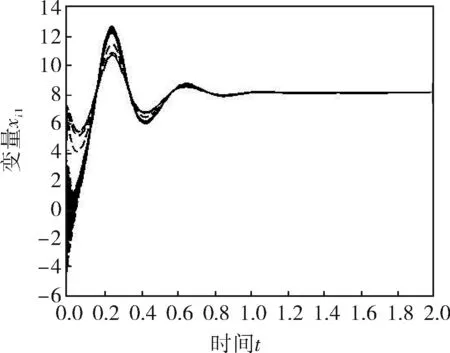
a. xi1

b. xi2

c. xi3

a. xi1

b. xi2

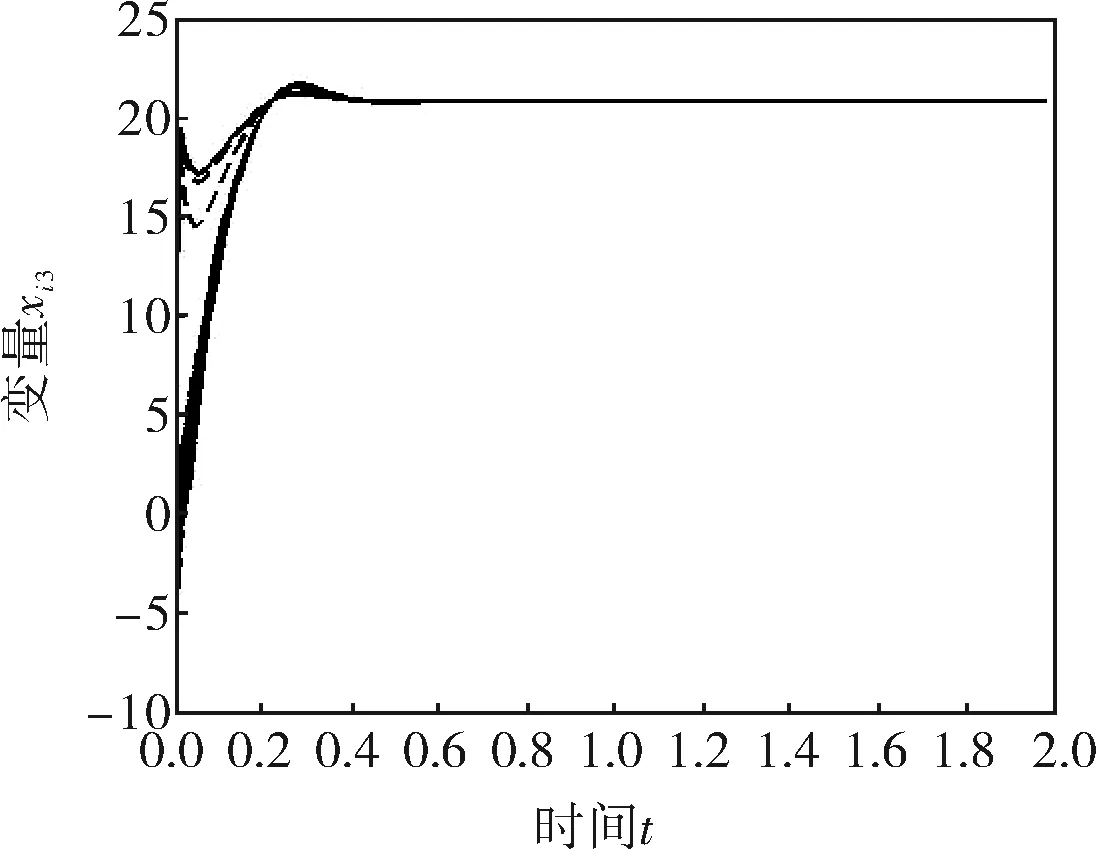
c. xi3

仿真结果表明，所有的智能体都能很好地跟踪固定目标。通过对比图2、3，不难发现事件驱动函数的发生阈值β越大，多智能体越早完成了跟踪任务。

3 结束语

提出一种新型的基于事件驱动的多智能体固定目标跟踪算法。理论和仿真结果表明，随机分配系统中所有智能体的初始状态，经过一段时间的调整，最后系统能够跟踪到目标，并且进入稳定状态。即该固定目标跟踪控制算法是切实可行的。

[1] Wang X F, Chen G R.Pinning Control of Scale-free Dynamical Networks[J]. Physica A:Statistical Mechanics and Its Applications，2002, 310(3-4):521～531.

[2] Li X, Wang X F,Chen G R.Pinning a Complex Dynamical Network to Its Equilibrium[J].IEEE Transactions on Circuits and Systems I: Regular Papers,2004, 51(10):2074～2087.

[3] Lu W L, Chen T P. New Approach to Synchronization Analysis of Linearly Coupled Ordinary Differential Systems[J].Physica D:Nonlinear Phenomena, 2006, 213(2):214～230.

[4] Olfati-Saber R,Jalalkamali P.Coupled Distributed Estimation and Control for Mobile Sensor Networks[J].IEEE Transactions on Automatic Control, 2012, 57(10):2609～2614.

[5] Gupta R, Bandyopadhyay B, Kulkarni A M.Power System Stabilizer for Multi-machine Power Systems Using Robust Decentralized Periodic output Feedback[J].IEEE Proceedings of Control Theory and Applications, 2005,152 (1):3～8.

[6] Chen T P, Liu X,Lu W L. Pinning Complex Networks by a Single Controller[J].IEEE Transactions on Circuits and Systems I-Regular Papers,2007, 54(6):1317～1326.

[7] Zhan M, Gao J H,Wu Y,et al.Chaos Synchronization in Coupled Systems by Appling Pinning Control[J].Physical Review E, 2007, 76:36203.

[8] Lu W L. Adaptive Dynamical Networks via Neighborhood Information：Synchronization and Pinning Control[J].Chaos: An Interdisciplinary Journal of Nonlinear Science, 2007, 17(2):23122.

[9] Zhou J, Lu J A,Lu J H. Pinning Adaptive Synchronization of a General Complex Dynamical Network[J].Automatica,2007, 44(4):996～1003.

[10] Sorrentino F,Bernardo M D,Garofalo F,et al. Controllability of Complex Networks via Pinning[J].Physical Review E，2007, 75:46103.

[11] Amaral L A N,Guimera R. Lies, Damned Lies and Statistics[J].Nature Physics，2006, 2(2):75～76.

[12] McGraw P N, Menzinger M. Clustering and the Synchronization of Oscillator Networks[J].Physical Review E,2005, 72:15101.

[13] Kim B J. Performance of Networks of Artificial Neurons: The Role of Clustering[J].Physical Review E,2004, 69:45101.

[14] Li X, Chen G R.A Local-world Evolving Network Model[J].Physica A: Statistical Mechanics and Its Applications,2003, 328(1-2):274～286.

[15] Barrat A, Weigt M. On the Properties of Small-world Network Models[J].European Physical Journal B,2000, 13(3):547～560.

[16] Boccaletti S, Latorab V, Moreno Y,et al.Complex Networks:Structure and Dynamics[J].Physics Reports,2006, 424(4-5):175～308.

[17] Li X, Wang X F.Controlling the Spreading in Small-world Evolving Networks: Stability, Oscillation,and Topology[J].IEEE Transactions on Automatic Control,2006, 51(3):534～540.

[18] Restrepo J G, Ott E,Hunt B R.Onset of Synchronization in Large Networks of Coupled Oscillators[J].Physical Review E,2005, 71:36151.

[19] Chen G, Ueta T.Yet another Chaotic Attractor[J]. International Journal of Bifurcation and Chaos,1999，9(7)： 1465～1466.

[20] Barabasi A L. Linked: The New Science of Networks[M]. Massachusetts: Persus Publishing，2002.

ANovelControlAlgorithmforMulti-agentFixedTarget

QIN Bu-zhi

(DepartmentofAutomation,NanjingPolytechnicInstitute)

A novel control algorithm for multi-agent fixed targets was proposed. When an agent reaches the region nearby the fixed target, adding a feedback controller between this agent and the tracking target can reduce communication load there effectively. Simulation result proves effectiveness of this algorithm proposed.

multi-agent, fixed target, control algorithm

TP393

A

1000-3932(2017)03-0258-04

江苏省2014年青蓝工程资助项目；江苏省第五期“333高层次人才培养工程”培养对象项目。

秦补枝(1975-)，副教授，主要从事非线性控制和复杂网络分析与控制方向的研究，68084819@qq.com。

2016-09-26)